基于分子动力学方法研究间规聚丙烯温度相关性的热输运性质

高建树，邵磊山，刘 洋，李静静，蒋文军，何 慧

（1.中国石化 茂名分公司研究院，广东 茂名 525000；2.华南理工大学 材料科学与工程学院，广东 广州 510006）

间规聚丙烯由茂金属催化剂催化丙烯聚合而 成[1]，其立体结构中的甲基侧链分别交替规则地排列于主平面的两侧[2]。与等规聚丙烯相比，间规聚丙烯特殊的结构使它的力学性质和光学性质均有较大的提升[3-5]。然而，间规聚丙烯分子链上甲基侧链交替的结构，也改变了间规聚丙烯分子自身的运动以及分子间的相互作用力[6]。特别地，间规聚丙烯热输运过程由声子输运组成，其声子群的运动方式对热输运过程有着重要影响[7]。因此，针对间规聚丙烯的热输运，开展相关的研究以及分析物理机制，尤其是获取在常见应用温度下的热传导规律具有重要的现实意义。

由于间规聚丙烯中的分子链相互缠绕，因此聚合物内部的热输运形成了错综复杂的热阻网络。Kovalchuk等[8]采用平面热源法测得间规聚丙烯复合材料的热导率为0.256 W/（m·K），并指出间规聚丙烯在掺杂纳米颗粒时将引入额外的接触热阻，界面处的声子散射抑制了热导率的提高。Leung[9]指出在晶体区域，高度有序分子链的协调振动可增强热传导，通过对聚丙烯分子链的外力拉扯，可增加聚丙烯分子排列有序度，同时提升热传导性能。间规聚丙烯的熔点相比聚乙烯更高[10]，通常大于397 K[11]，在耐低温抗冲透明容器、薄膜、医用灭菌容器、注射器和透明片材等领域有广泛的使用前景[12]。间规聚丙烯应用于270～390 K的环境下，而针对温度对间规聚丙烯内部复杂传热过程的影响，亟需对它的微观传热机理开展进一步的研究工作。

对于微观传热过程中热载流子的输运过程，通常采用声失配模型（AMM）和散射失配模型（DMM）分析声子在界面处的传递过程[13]，其中，AMM考虑的是声子在界面传输时的镜面透射过程，而DMM考虑的是声子在界面传输时的扩散透射方式。声子Boltzmann方程中将声子视为准粒子[14]，在弛豫时间近似下，利用微扰理论获得弛豫时间，同时考虑非简谐性声子相互作用（如三阶和四阶声子散射过程）对热导率的影响，通过求解Boltzmann方程计算热导率[15]，并分析不同光学声子支和不同声学声子支对热导率的贡献[16]。分子动力学方法通过求解体系中原子的牛顿运动方程获得原子的运动轨迹，并运用统计学方法获得平衡态下的热力学参数，考虑了非简谐性声子相互作用的所有阶项[17-18]，该方法已被证明可有效用于分析热输运过程中的热载流子行为[19-20]。

本工作采用非平衡分子动力学方法，通过分析聚合物密度确立了一定分子聚合度的间规聚丙烯模型，并采用该模型分析了间规聚丙烯聚合物在常规使用温度下的热传导性质，研究了温度对间规聚丙烯热导率的影响、温度相关性速度自相关函数及声子振动态密度的变化规律，从分子运动层面上揭示间规聚丙烯的微观热传导机制。

1 模拟部分

1.1 模型的构建

间规聚丙烯的模型见图1。如图1所示，间规聚丙烯模型沿z轴方向分别为真空层、固定层、热流流进层、间规聚丙烯层、热流流出层、固定层和真空层。间规聚丙烯层的几何尺寸为3.3 nm×3.3 nm×17 nm，而热流流进层和热流流出层的厚度分别为2 nm。为避免间规聚丙烯模型出现结构松散的现象，模型两端均设置了厚度为3 nm的固定层。此外，为了防止模型端部分子及原子发生可能的相互作用，在模型两端设置了厚度为2 nm的真空层。间规聚丙烯自身的热运动及分子间的相互作用力采用聚合物一致性力场进行描述，该势函数已被验证可准确且有效地用于分析聚丙烯分子的相互作用[21-23]，利用开源软件LAMMPS中的分子动力学模拟软件进行研究。

图1 间规聚丙烯的模型Fig.1 Model of syndiotactic polypropylene(s-PP).

1.2 计算细节

模拟体系首先对在标准大气压对应压力下的等温等压系综（NPT）进行分析，以控制体系的致密度，NPT的粒子数、压强和温度均保持恒定，平衡时间设置为1 ns，选用对称性边界条件。当体系的致密度稳定后，使用正则系综进行驰豫，在该体系中，模型的粒子数、体积和温度均保持不变，平衡时间设置为3 ns。当完成驰豫后，进一步采用微正则系综进行分析，即体系中的粒子数、体积和总能量控制为一个恒定值，平衡时间设置为3 ns，以保证体系中的间规聚丙烯层建立起稳定的温度梯度。步长设置为0.5 fs。当在热流流进层和热流流出层中不断输入与输出一个恒定热流时，间规聚丙烯层中将产生稳定的温度梯度，温度分布通过额外统计0.5 ns平衡时间内的平均值获得，如图2所示。基于傅里叶导热定律，间规聚丙烯的热导率（k）可通过统计热流大小和温度分布梯度获得：

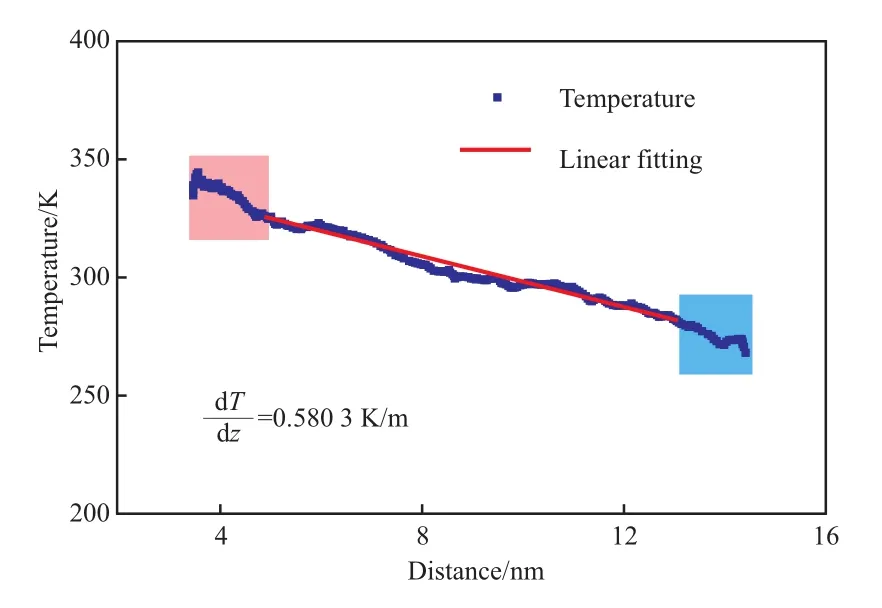
图2 模型体系沿着z轴方向的温度分布Fig.2 Temperature profile along the z direction.

式中，q为热流密度，W/m2；Q为单位时间的传热热量，W；A为沿着z方向的横截面面积，m2；Δz/ΔT为沿着z方向温度梯度的倒数，通过统计z方向的温度分布并由线性拟合得到斜率的倒数所确定。为了计算结果的准确性和稳定性，任意温度下获得的计算结果由3次独立的计算值（赋予不同的初始速度分布）取平均，并且计算误差由结果的标准差确定。

2 结果与讨论

2.1 间规聚丙烯分子聚合度的确定

间规聚丙烯的分子量较大，若构建聚合度较大的分子模型用于计算，将会浪费大量的计算时间。但当构建模型的间规聚丙烯聚合度过小时，则不能反映聚合物的真实性质。为了确定聚合度适合的间规聚丙烯模型，有必要研究聚合物密度与间规聚丙烯聚合度之间的关系。图3为300 K下间规聚丙烯的密度随聚合度的变化规律。从图3可看出，随着间规聚丙烯的聚合度由3增至80，聚合物的密度由0.639 g/cm3增至0.798 g/cm3。当间规聚丙烯的聚合度达到50后，聚合物密度几乎不发生变化。因此，本工作选用聚合度为50的间规聚丙烯分子用于构建聚合物热导率的分析模型，可确保能反映间规聚丙烯聚合物的真实性质且计算量适中。

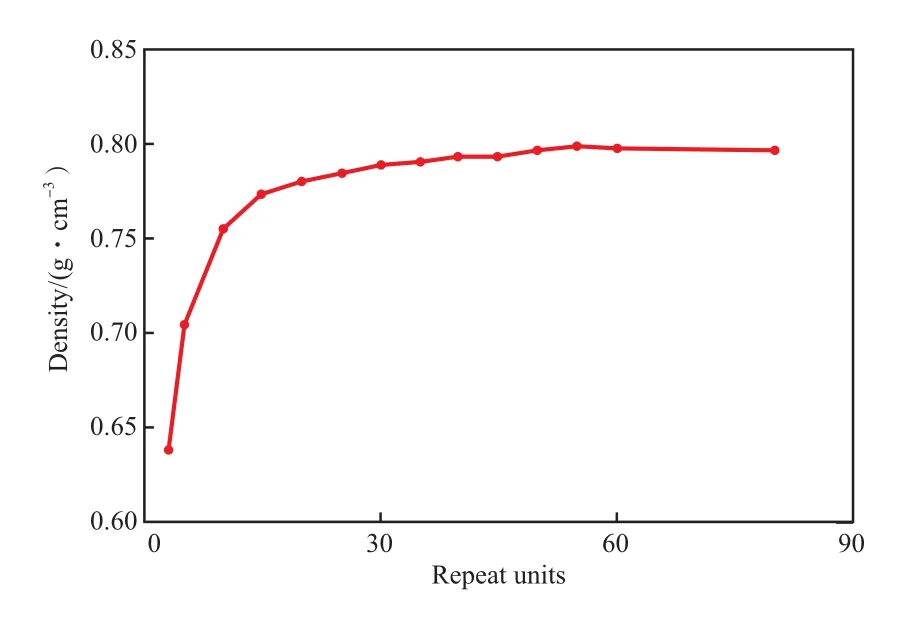
图3 300 K下间规聚丙烯的密度与聚合度的关系Fig.3 The calculated density of s-PP versus their polymerization degree at 300 K.

2.2 不同聚合度下的声子群运动

通过对不同聚合度聚丙烯速度自相关函数的分析，可以定量地获得分子链长度对间规聚丙烯运动形式的影响。速度自相关函数的定义为：

式中，Z（t）为随时间变化的速度自相关函数；v（0）为初始时刻的速度，m/s；v（t）为t时刻的速度，m/s。在一定温度下，体系粒子速度的大小和方向均随时间的推移而发生变化，因此，可预见的是，Z（t）将随时间不断衰减，当t很大时，Z（t）趋于0[24-26]。

300 K下不同聚合度间规聚丙烯随时间变化的速度自相关函数和声子振动态密度分布见图4。由图4a可知，不同聚合度的间规聚丙烯随时间变化的速度自相关函数呈相似的变化规律，均由1逐渐振荡波动至0，表明间规聚丙烯分子在其局部位置不断发生振动[27]。且随时间的延长，原子的运动速度与初始值的相关性逐渐减小。随着间规聚丙烯聚合度由3增至50时，速度自相关函数的第1个波谷深度也由-0.418逐渐变化至-0.432，说明随聚合度的增加，间规聚丙烯分子链的运动惯性增大，且分子链发生相互缠绕的几率也增加[28]，整体运动速度将更加不容易发生改变。通过将速度自相关函数进行快速傅里叶变换，便可得到声子振动态密度分布（G（ω））：

式中，ω为振动波数，m-1；i为虚数单位。振动态密度的分布说明了聚合物内部热载流子振动频率的信息，而振动态密度的强度则反映了热载流子对应某一频率的群数量。由图4b可以看出，间规聚丙烯的声子振动态密度存在两个峰值，分别分布于40～50 THz和80～98 THz处。随着聚合度的增加，声子振动态密度在低频段0～20 THz处的强度有所减小，同时在40～50 THz处的波峰朝着高频分量拓展，并且80～98 THz处的波峰强度也有所提高。

图4 300 K下不同聚合度间规聚丙烯随时间变化的速度自相关函数（a）和声子振动态密度分布（b）Fig.4 Evolution of velocity autocorrelation function(VACF) over time(a) and phonon vibrational density of state(PDOS)(b) for s-PP with different polymerization degree at 300 K.

2.3 不同温度下的热传导性质

在间规聚丙烯的常规使用温度270～390 K范围内，热导率的计算结果见图5。从图5可看出，随温度的升高，热导率由（0.202±0.004 5）W/（m·K）增至（0.241±0.000 9）W/（m·K），提升19.3%。该计算结果与文献[29-30]中的分析结果相近，进一步验证了计算分析的准确性。间规聚丙烯聚合物由相互缠绕的分子链复杂网络组成，结构中没有固定规律排列的分子秩序[31]。间规聚丙烯的热输运是依靠分子链自身的晶格振动及分子间的相互作用力进行的，即声子输运作为主导形式进行热量传递。当温度升高时，聚合物分子链的平均间隙增大，使得分子链间范德华力作用的影响变小，但温度升高加剧了分子链的振动和迁移，使得它自身的移动和形态调整变得更灵活，可填补聚合物中可能存在的空间间隙[32]。与此同时，随温度的升高分子链的相互缠绕更为紧密，分子链间的接触面积增加，这也有利于分子链间进行更高效的能量传递[33]，使得聚合物的热导率得到提高。

图5 间规聚丙烯热导率随温度的变化关系Fig.5 Thermal conductivity of s-PP versus temperature.

2.4 不同温度下的声子群运动

从分子链运动对传热过程的影响看，由于间规聚丙烯的热导率与分子链的振动及运动形式有关，而聚合物的速度自相关函数可以直观地反映间规聚丙烯分子在分子链相互耦合下的运动过程[34]。当体系温度发生变化，若间规聚丙烯分子的运动完全局域化而不受周遭其余分子链运动的影响或者影响减小（相互耦合程度减弱）时，其速度自相关函数将快速发生衰减，说明热量在分子间的输运阻力提高，热导率减小；反之，则说明其分子间的相互耦合程度增强，热量在分子间进行输运的阻力减小[35]。

间规聚丙烯在不同温度下的速度自相关函数分布和声子振动态密度分布如图6所示。从图6a可看出，随着温度从270 K逐渐升至390 K，速度自相关函数的第1个波谷深度由-0.449变化至-0.368，绝对值呈降低的趋势。这说明当温度越高时，间规聚丙烯的分子振动将越剧烈。与此同时，间规聚丙烯分子间的相互耦合程度得到提高，有利于热量在间规聚丙烯分子间进行传递。从图6b可看出，不同温度下间规聚丙烯的声子振动态密度具有不同的分布形式。其中，间规聚丙烯的声子振动态密度存在两个峰值，分别分布在40～48 THz和82～94 THz之间。可以看出，当体系温度逐渐升高时，间规聚丙烯在0～40 THz处的声子振动态密度强度逐渐减小。对于40～48 THz处的振动态密度，虽然波峰峰值随温度的升高逐渐减小，但波峰宽度却不断增加，并朝着高频分量拓展。该部分的改变是因为当温度升高时，低频段（0～40 THz）的声子群受到热激发而往较高频段40～48 THz转变。对于单个热载流子，高频段热载流子携带的能量要高于低频段热载流子携带的能量[36]。随着间规聚丙烯的声子群由低频段向高频段移动，单位热载流子的平均可携带能量将增加。因此，当温度升高时，高频段的声子群在单位时间内将携带更多的热量沿着z轴传递，从而有利于改善其热输运性能，间规聚丙烯的热导率得到提升。

图6 间规聚丙烯在不同温度下的速度自相关函数（a）和声子振动态密度分布（b）Fig.6 VACF(a) and PDOS(b) for s-PP at various temperatures.

3 结论

1）构建了间规聚丙烯模型，沿z轴方向分别为真空层、固定层、热流流进层、间规聚丙烯层、热流流出层、固定层和真空层。

2）随间规聚丙烯聚合度的增大，聚合物密度增加，当聚合度为50时，密度趋于平稳，此时间规聚丙烯可用于构建热导率的分析模型，能反映间规聚丙烯聚合物的真实性质且计算量适中。

3）随聚合度的增加，间规聚丙烯分子的第1个波谷深度的绝对值略有增加，声子振动态密度在低频段0～20 THz的强度有所减小，在高频段80～98 THz范围处的波峰强度增强。

4）当温度由270 K升至390 K时，间规聚丙烯的热导率由0.202 W/（m·K）增至0.241 W/（m·K），速度自相关函数的第1个波谷深度绝对值由0.449减小至0.368，0～40 THz处的低频分量逐渐减小，而40～48 THz处的高频声子群的数量有所增加，高频段的声子群在单位时间内将携带更多的热量沿着z轴进行传递，从而有利于改善间规聚丙烯的热输运性能。