极地探险邮船顶推结构强度计算方法

朱红娟，葛珅玮，张 卫

(1.招商局邮轮制造有限公司，江苏 南通 226116；2.江苏航运职业技术学院，江苏 南通 226010)

0 引 言

极地探险邮船平地建造，在拉移上半潜驳船后，通过半潜驳船下潜完成下水[1]，同时需要通过拖船顶推邮船，将其靠在码头边上。顶推作用点通常局限在船体舷侧首、中、尾的某些区域范围内，顶推载荷通过拖船首部绑扎的2个轮胎传递。邮船的构件板厚薄[2]、骨材和T排结构尺寸远小于一般的货船。如果在顶推过程中，舷侧外板和骨材由于强度不足而失效，易影响交船周期，对邮船公司和船厂造成巨大的损失[3]。

极地探险邮船是国内建造的中小型豪华邮船船型。在此之前，我国在豪华邮船建造领域几乎处于空白状态[4]，规范中也无相关顶推结构强度计算的规定。在通常情况下，可采用结构有限元仿真法校核顶推状态下船体舷侧的结构强度。有限元计算的前提是对目标分析区域周边一定范围的结构进行建模，直接计算工作量大。在实际过程中，邮船船体会存在多个顶推点，需要建立多个局部模型，建模的工作量巨大，时间成本较高。

通过对载荷和边界的提炼建立简化梁系模型，对顶推过程进行快速计算并将计算结果与有限元仿真的结果进行对比，为顶推结构强度校核提供一种省时省力的方法。

1 邮船顶推方案

极地探险邮船在通过驳船拉移下水漂浮后，至码头边还有一定的距离，需要通过拖船顶推作业，将邮船推到码头边上。具体顶推位置如图1所示。共有3个，分别位于舷侧的首部、中部和尾部。

图1 顶推位置范围

考虑拖船控制的精度问题，实际顶推点的范围可能会与具体位置存在一定的偏差。以尾部的顶推点为例，顶推纵向位置控制在FR3～FR0，垂向位置控制在距基线7 250～9 970 mm。

2 有限元数值仿真

2.1 有限元模型

采用通用有限元软件Femap with Nastran建立尾部有限元模型，有限元网格大小为700 mm×800 mm。尾部模型的甲板、横舱壁、横梁腹板等主要结构均采用4节点的板单元模拟，在高应力区尽可能避免使用三角形单元。顶推目标区域采用大小为50 mm×50 mm的细网格，纵骨腹板和面板均使用4节点的板单元模拟，如图2所示。

图2 艉部有限元模型

2.2 载荷与边界条件

2.2.1 载 荷

对极地探险邮船尾部舷侧顶推位置处结构施加载荷。根据轮胎接触面积施加，施加在较危险的位置处。纵向T排跨度最大、轮胎仅作用在一根纵骨上的情况为较危险工况，选取该工况作为研究工况。拖船的顶推力F最大为15 t。假设轮胎与船体接触面均匀传递载荷，在实际接触位置处施加均布载荷P0。实际施加载荷如图3所示。

图3 载荷图

(1)

式中：A0为2个轮胎与外板的直接接触面积。

2.2.2 边界条件

FR45肋位截面简支约束(1,1,1,0,0,0)，其中：1代表固定；0代表释放。

2.3 强度评估标准

参照劳氏船级社PrimaryStructureofPassengerShip第16.16节[5]相关内容，X正向许用应力为

σx=0.92σL

(2)

X正向应力许用衡准为σx=300.3 MPa。

2.4 计算结果分析

对结构进行有限元分析，目标梁的应力云图如图4所示。

图4 舷侧纵骨正应力分布

由图4可知:目标型材X向最大正应力值位于型材中心面板处。面板发生弯曲变形，主要受力模式为弯曲拉应力。X向最大正应力值为207.7 MPa。因此，当轮胎直接作用在外板上时，有限元计算出的结果满足规范强度要求。

3 简化梁系计算

在拖船顶推时，固定2个轮胎，顶推载荷通过轮胎传递至舷侧板架上，纵骨间距为680 mm，肋骨跨距为2 400 mm和800 mm，纵骨大小为HP140 mm×8 mm，外板板厚为8.5 mm。轮胎外径D为1 100 mm，内径d为500 mm。与有限元仿真类似，考虑较危险状态，2个轮胎直接作用在跨度较大的一根舷侧纵骨上，如图5所示。对这种较危险的工况展开有限元分析。

图5 轮胎作用在较危险处

3.1 单跨梁计算

拖船的顶推力通过轮胎直接作用在舷侧外板和纵骨上，取纵骨及其带板作为研究目标，假设顶推力通过轮胎均匀作用在外板上，轮胎与纵骨接触简化为4个受力点。梁系简化模型如图6所示，其中：Q1为轮胎产生的均布载荷，在进一步简化后，将轮胎与纵骨接触的均布载荷简化为集中载荷，载荷作用点P位于轮胎宽度的中心点处；载荷作用点2P位于2个轮胎的接触点；T排支撑骨材端部处简化为简支；a为集中载荷间距；L2为简支梁跨距。

图6 单跨梁模型

假设4个受力点受力相同，每个点的集中力大小为

(3)

集中载荷间距为

(4)

带板宽度B2=min(0.2L2，S)= 480 mm，其中：S为纵骨间距。骨材及其带板的剖面模数Z=1.26×105mm3。骨材及其带板的惯性矩I2=1.03×107mm4。

查单跨梁的弯曲要素表，梁上中间集中载荷2P作用下的最大弯矩为

(5)

梁上两边集中载荷P作用下的最大弯矩为

(6)

将上述2种集中载荷作用下的弯矩叠加，得到梁中心点的最大弯矩为

(7)

梁中心点的最大应力值为

(8)

σmax1>σx=300.3 MPa

(9)

单跨梁简化计算的结果与有限元仿真的结果大相径庭，且计算结果远大于有限元值，如果按照该方式进行强度评估则需要进行补强，会造成一定的资源浪费。因此，直接简化为单跨梁是不适合的。如排除载荷简化的影响，继续考虑3跨梁的计算。

3.2 3跨梁计算

根据实际船体结构尺寸，考虑3跨梁作为研究对象，将原来支座断面切断，拆分为两端自由支持的单跨梁，断面上出现弯矩，该弯矩反映原来相连的两段梁在支座断面中力的互相作用，在切开的断面上互为作用力与反作用力。3跨梁简化及载荷分解如图7所示，其中：m2、m3分别为点2和点3的端部弯矩；L2、L3为简支梁不同跨距；θ21、θ23、θ32、θ34分别对应点1、点2、点3和点4的转角，b、c分别为载荷作用点P至点2和点3的距离。由于原来的3跨梁是连续的，切开后仍应保持变形的连续条件，弯矩的大小应恰好使梁1-2与梁2-3在2点有相同的转角，即θ21=θ23。同理，θ32=θ34。将中间一段梁上的载荷分为3部分考虑，每部分载荷可查单跨梁的弯曲要素表。

图7 3跨梁简化及载荷分解示例

梁3-4的带板宽度B3=min(0.2L3，S)= 160 mm；梁3-4的骨材及其带板的惯性矩I3=7.7×106mm4。

根据转角相同可得2个转角等式：

(10)

(11)

式(10)和式(11)中：E为材料的弹性模量，E=2.06×105N/mm2。

通过式(10)～式(11)算得：m2=1.64×107N·mm；m3=2.55×107N·mm。

梁中心最大X正向应力值为

(12)

通过3跨梁简化计算，在考虑目标梁两端断面弯矩后，梁中心最大X正向应力值为255.7 MPa，计算结果满足规范强度要求。相比单跨梁计算的X正向最大应力值大幅下降，减少39.4%；与有限元结果对比相差23.1%。

可见目标梁两端支座面中的弯矩值占比较高，不宜直接简化为单跨梁。如果直接简化为单跨梁，会导致设计过于保守，产生不必要的额外加强，浪费大量的人力和物力。

3.3 5跨梁计算

鉴于3跨梁计算结果与有限元相差23.1%，继续研究5跨梁结构，计算方法与第3.2节一致。因尾部存在大梁和外板支撑，边界条件简化为简支，L1=1 632 mm，简化结构模型如图8所示，其中：m1、m2分别为点1和点2的端部弯矩；θ10、θ12、θ43、θ45分别对应点1～点5的转角，L1为起始点至点1的简支梁跨距。

图8 5跨梁模型

梁0-1的带板宽度B1=min(0.2L1，S)= 326.4 mm；梁0-1的骨材及其带板的惯性矩I1=9.5×106mm4。

根据转角连续得：

θ10=θ12

(13)

θ21=θ23

(14)

θ32=θ34

(15)

θ43=θ45

(16)

查单跨梁的弯曲要素表，可得：

(17)

(18)

(19)

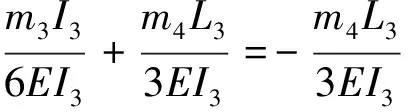
(20)

通过式(17)～式(20)算得：m2=3.48×197N·mm；m3=2.02×107N·mm。

梁中心最大应力值为

(21)

在考虑5跨梁的断面弯矩后，梁中心最大应力值相比3跨梁减少20.1%，与有限元计算结果相差仅为1.6%。可见考虑的梁跨数越多，计算结果越接近有限元仿真值。

3.4 结果分析

将梁系计算结果和有限元仿真结果对比，如图9所示。5跨梁计算的正应力值与有限元仿真结果仅有1.6%的偏差。随着考虑的梁跨数越多，计算得出的X向正应力水平越低，越接近有限元结果。因此当项目时间比较紧张时，推荐使用5跨梁计算方法进行校核，通过转角连续，列出4个方程，可快速计算出目标梁两端面的弯矩m2、m3。

图9 正应力变化趋势图

对于强度校核而言，5跨梁计算精度较高，可代替有限元计算，省去针对大量局部结构的有限元建模的工作量。如果纯粹出于强度校核的目的，当3跨梁计算的结果满足强度要求时，也可不继续计算5跨梁计算结果。

4 结 论

主要讨论在极地探险邮船顶推作业时舷侧骨架结构强度的计算方法，结论如下：

(1)顶推计算通常可采用有限元仿真方法。但如果顶推点众多，需要建立多个局部有限元模型，涉及船首、船中和船尾，建模工作量较大，需要耗费的时间成本较高。

(2)为不影响现场的施工周期，快速响应现场需求，可考虑简化载荷，建立多跨梁系模型，快速计算正应力。

(3)随着考虑的梁跨数越多，计算得出的X向正应力越低，5跨梁的计算结果与有限元仿真结果较为接近。

(4)如仅出于强度校核考虑，3跨梁计算已能满足规范强度要求，则可不必计算5跨梁系。如3跨梁计算结果不满足规范强度要求，建议继续计算5跨梁。如5跨梁仍然不满足规范结构强度要求，则应给出相应的加强方案。