借助空间向量,妙解图形折叠问题

李福全

(河北省任丘市第一中学)

图形折叠问题是高考空间立体几何中比较常见的一类问题,这类问题是指将一平面图形翻折后变成空间几何体,然后根据平面图形的数量关系研究空间几何体中各元素数量关系的问题.解决这类问题的关键是确定翻折前后相关元素的不变量与变化量,运用空间向量知识加以分析.

1 判定命题

例1将正方形ABCD沿对角线BD折成直二面角,给出下列四个结论:①AC⊥BD;②AB,CD所成角为60°;③△ADC为等边三角形;④AB与平面BCD所成角为60°.其中真命题是________(请将你认为是真命题的序号都填上).

解析对于①,如图1所示,取BD的中点O,连接AO,CO,易知BD垂直于平面AOC,故BD⊥AC,①正确.

图1

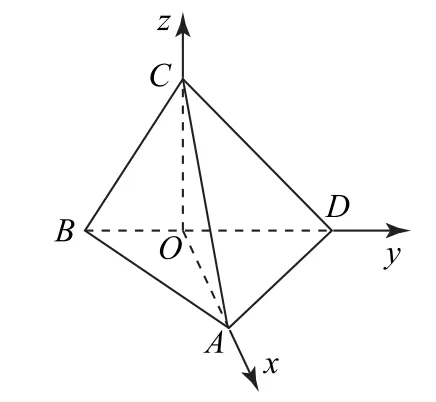
图2

对于③,在Rt△AOC中,由AO＝CO＝,得＝a,故△ADC为等边三角形,③正确.

对于④,易知∠ABO为直线AB与平面BCD所成的角,可求得∠ABO＝45°,故④错误.

综上,选①②③.

点评本题主要考查平面图形的折叠、空间线面位置关系的判定与性质、空间角的求解等知识.求解的关键是正确分析平面图形折叠后对应的立体几何图形,并能结合相应的性质加以分析与判定.

2 求解角度

例2如图3所示,在Rt△ABC中,∠C＝90°,BC＝3,AC＝6,D,E分别为AC,AB上的点,且DE∥BC,DE＝2.如图4所示,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD.

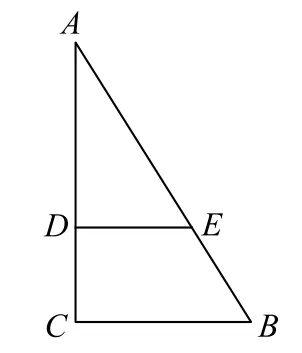
图3

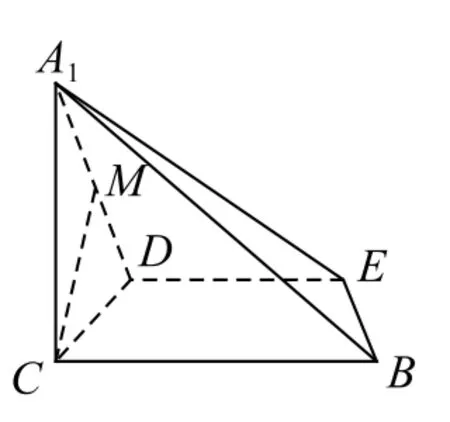
图4

(1)求证:A1C⊥平面BCDE;

(2)若M是A1D的中点,求CM与平面A1BE所成角的大小.

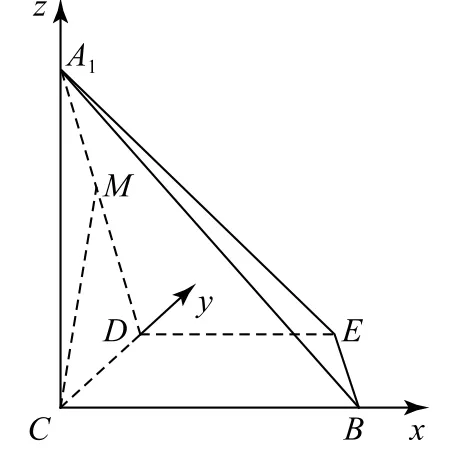
图5

点评本题主要考查空间几何中的线面位置关系及其判定、空间角的求解及其应用.在折叠过程中,要注意折叠前后对应直线的平行、垂直关系以及线段的长度等,进而为利用空间向量求解空间角奠定基础.

3 求解二面角的余弦值

例3如图6所示,在梯形ABCD中,AD∥BC,BE⊥AD于E,且DE＝2BC＝2BE,将梯形ABCD沿BE折叠成如图7所示的几何体,∠AED＝为AE的中点.

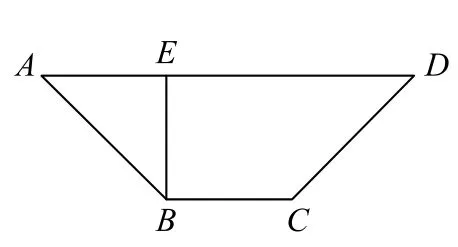
图6

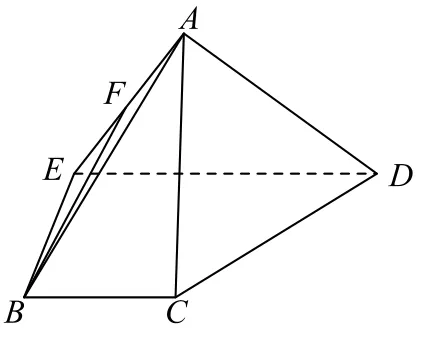
图7

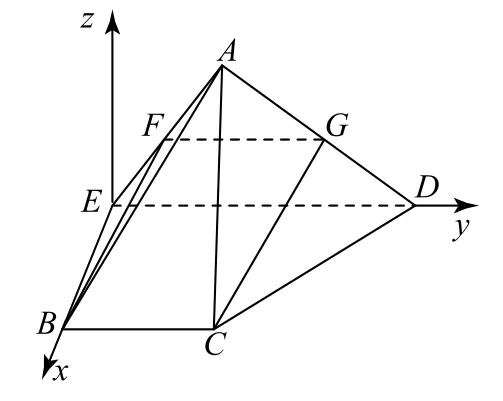
图8

点评本题主要考查线面平行的证明、二面角的计算、空间向量及其应用等知识,意在考查学生的转化能力和计算求解能力.

平面几何图形折叠成空间几何体的变换问题难度比较大,对空间想象能力要求较高.这类问题主要对空间几何体中的点、线、面沿着相应的直线进行折叠变换,设置角度、距离、轨迹等众多问题,探求定值、最值等,是一类思维方式多样、难度较大的创新性问题,也是模拟考试、高考、自主招生考试中的热点问题,具有很好的选拔性与区分度.

(完)