航空公司航线可更换件需求预测模型比较分析

曹允春，刘宇展，沈丹阳

(中国民航大学 1.交通科学与工程学院；2.经济与管理学院；3.临空经济研究中心，天津 300300)

受到新冠肺炎疫情影响，截至2022年上半年，我国航空公司资产负债率达82.2%，有12家航空公司资产负债率超过100%；其中三大航(中国国际航空股份有限公司、中国东方航空股份有限公司、中国南方航空股份有限公司) 亏损近497亿元，已经超过了去年全年3家航空公司的全部亏损。与此同时，全球航空客运复苏慢于预期，IATA预测2024年全球航空客运需求(按RPK计算) 才将恢复到2019年的水平。在需求疲软的情况下，成本管控成为了各大航空公司的重点工作。

航空公司总运营成本中，维修成本所占比重约为20%～35%，而航材消耗则占到整个维修费用的60%～70%。其中，飞机在航线维修期间，可以用标准工具在飞机上轻松更换的产品被称为航线可更换单元(line replaceable unit，LRU)，如零组件、设备、结构件等[1]。部分重要的LRU件“技术上可维修、经济上合算”，采购及库存占用巨额资金。根据帕累托法则，高价值可维修件管理遵守“二八定律”。占航材数量仅有20%的高价值航材，其采购和存储费用却可以占到航空公司相关总成本的80%。可见，科学的航材需求计划，尤其是高价可修LRU件需求的准确预测，是航空公司降低运营成本的有效途径之一。

本文对高价可修LRU件需求预测模型进行选择，建立有效性分析规则，选择航空公司高价可修LRU件故障数据，进行预测与分析，得出最优模型并对结果进行讨论。

1 文献综述

国内外有关航材的研究主要集中在需求预测、库存控制策略、供应商选择等几个方面。按照应用领域的不同，研究分为军备航材研究和民航航材研究。按照管理主体和对象不同，民航航材研究分为制造商航材研究和航空公司航材研究。

现有的航空公司航材研究中，针对航材消耗件的研究较为深入[2]。航材消耗件数量大，种类多，相对价值低，但过高的储备量仍会导致保管成本的增加，而储备量过少，则有可能出现由于航材消耗件缺货而造成飞机停场。因此航材消耗件的研究致力于探索如何在较低的库存持有水平上，维持较高的航班保障率，通过需求预测，来确定订货点和采购数量。相比之下，针对航材可修件的研究尚待深入。根据不完全统计，大多数航材可修件属于“NO GO件”，一旦发生缺货，必造成飞机停场[3]。

现阶段关于航空公司航材需求的研究，主要集中于以备件需求理论[4]为基础，进行预测方法的创新探讨，如利用机队的消耗数据和飞机的周转率数据进行双层组合预测[5]；提出新的多成分积累和高分辨率分析预测方法[6]；使用Croston深度预测方法对航空发动机需求进行预测[7]等。已有研究指出，航材消耗件与可修件都呈现出质量要求高、比强度与比刚度高、成本高等特点，导致其故障率远小于其他一般备件，故障次数符合间歇性需求特征[8]，并可以使用Croston改进算法、时间聚合方法等进行备件需求预测[9]。对于以上航材需求预测的大部分研究都只局限于单一预测模型，少量国内外学者利用组合模型来预测航空备件需求量[10]。

研究表明，科学地利用库存控制理论，也能有效地降低航空公司的管理成本。为了保障飞机日常飞行，降低飞机停场频率并降低航材支出成本，传统库存航材是按照保障率建模[11]，随着航空业高速发展，飞机种类日益增多，仓库管理成本增加，航空公司也开始利用航材故障数据、备件消耗来进行库存管理，涉及方法有Bootstrap方法[12]、二项分布[13]、METRIC模型[14]等。

虽然与民航航材在管理目标、保障率限定、使用环境、技术要求、需求影响因素等存在诸多不同[15]，但关于军备航材需求预测的一系列研究[16-17]，以及一些企业针对仓库物料进行需求预测[18]都为民航航材需求预测提供了可借鉴的方法。

2 预测模型与有效性原则

2.1 传统预测模型

传统的LRU预测是根据飞机飞行小时、机队规模、周转时间、平均车间处理时间等因素进行的。具体而言，LRU航材需求期望E为

其中，H表示每年飞行小时(flight hours，FH) ；N为机队中的飞机数量；n表示单机安装数；R为平均非计划拆换间隔时间(mean time between unscheduled removal，MTBUR) ；T表示周转时间(turn-around time，TAT) 。

如果周转件的周转时间波动不大，可以将周转时间更改为平均周转时间。当某种LRU有r次送修记录，则每次送修周转时间Ti(i=1,2,···,r)变为

LRU航材需求期望E变为

根据需求期望E的大小利用高斯分布(4) 或泊松分布(5) 来计算推荐LRU件的采购数量m。

推荐LRU件的采购数量m计算公式为

其中，α为高斯因素；L为航班保障率要求。

2.2 计量预测模型选择

研究表明，回归分析、时间序列与灰色系统理论3类预测方法在对某些航材进行预测时效果较好。常见模型的特点、适用性、假设前提等见表1。

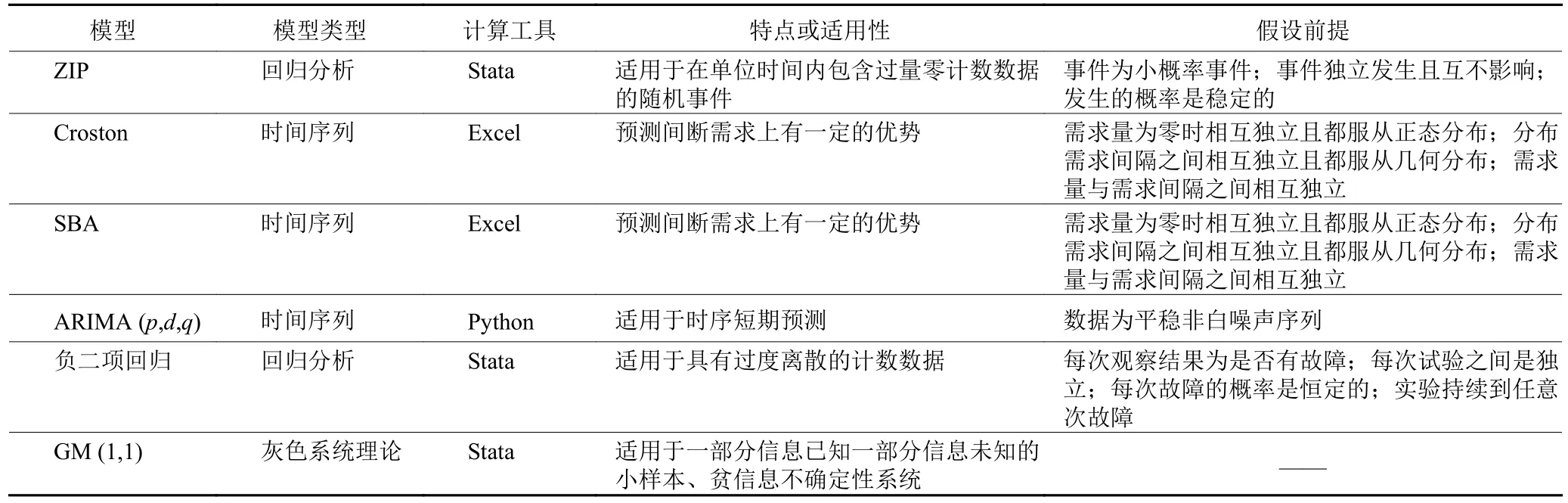
表1 模型特点与假设前提Table 1 Characteristics and assumptions of models

具体而言，各个模型原理与计算步骤如下。

2.2.1 零膨胀回归模型

零膨胀回归模型(zero-inflated poisson regression model，ZIP)，通常用于对于“0”数据占的比重远远超过其他取值的数据类型的预测中。

ZIP模型的基本原理是利用伯努利分布与普通计数分布混合计算，即

其中，ω为膨胀系数，且0≤ω＜1；f(yi)为生成的分布。

泊松分布是需求预测中常见的一种模型。令随机事件Y为“备件发生故障”，泊松分布可以表示单位时间内随机事件的数量，记作备件故障数。那么，泊松分布可以表示每单位时间内备件故障数的分布，其概率函数可表示为

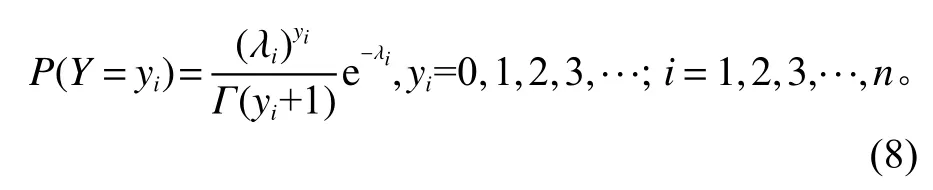
其中，yi为第i个月内故障的次数；λi为泊松参数，且满足E(Y)=µ=λi；Var(Y)=δ2=λi，µ为期望参数；δ2为方差参数。

当式(7) 中f(yi)为泊松分布时，则该零膨胀回归模型为零膨胀泊松回归模型，定义为

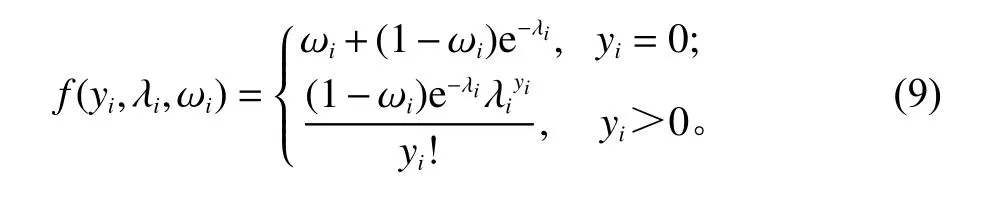
2.2.2 Croston模型

Croston[8]在研究库存控制时，发现以固定时间间隔计算可能会产生高达实际需求数量两倍的库存量，而这种现象好像是因为间歇性需求导致的，他针对间歇性需求的特征并基于指数平滑法提出了Croston模型。

设p个周期内的需求量为µ，需求Yt表示为

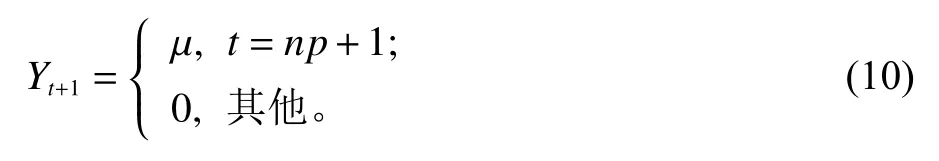
其中，n=1,2,···,p≥1。

将E(Yt)作为每个需求周期内的需求预测值µ/p，则

其中，α为平滑指数，0≤α≤1。

Croston模型假定上述需求到达时间间隔遵循随机分布，并在此基础上引入时间间隔和需求分布。将平均时间间隔和平均需求的指数平滑方法分开，将不连续序列分为两个子集，然后使用简单的指数平滑分别预测两个子序列。

=X(Ea-E1)=X(1-X)(Ea-Eb)=X(1-X)((A2+A4)Y-(A2-A3+A4))

其中，εt是第t期的预测误差；表示指数平滑后需求量中间间隔数量；是指数平滑后的需求量。下一期的需求预测为

2.2.3 SBA模型

Syntetos[19]认为在Croston模型中的计算结果存在不是无偏估计的可能，应加以调整，便提出了SBA模型，该模型指出预测值公式(14) 应为

2.2.4 ARIMA(p,d,q) 模型

ARIMA时间序列模型的基本思想是基于固定时间均衡时间序列数据或非平稳时间序列数据，来揭示目标变量与时间变量之间存在的过去和现在的规律，以及利用历史数据来预测给定时间点的情况。以备件历史故障次数为基础，ARIMA(p,d,q) 模型建立了故障预测模型，将备件故障时间设为Yt，得到一个新的时间序列Xt，则

其中，p、q分别为自回归阶数与滑动平均阶数；βi、αj为参数；ε(t)为白噪声序列。

2.2.5 负二项回归模型

很多学者认为，当数据的平均值与方差明显不相等，或者零点数据多次出现时，负二项回归模型比泊松分布回归模型更适合数据预测，可以提高模型对数据拟合的精度。负二项回归模型常用来预测需求、事故、故障、病情发生等概率，负二项分布概率函数形式为

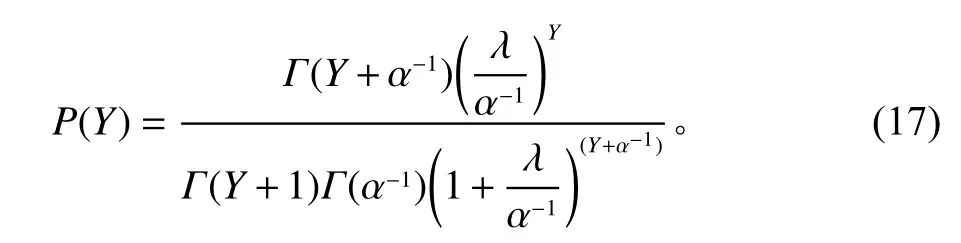
其中，µ为总体参数；α为离散参数；Y=0,1,2,···。

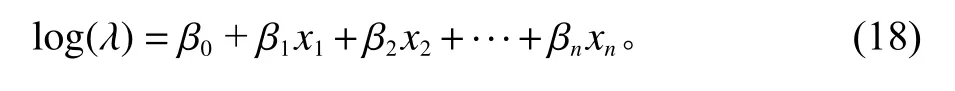
2.2.6 GM(1,1) 模型

GM(1,1) 模型是最常见的一种灰色模型，模型通过对数据进行累加从而弱化离散数据造成的波动性，设原始数据序列为

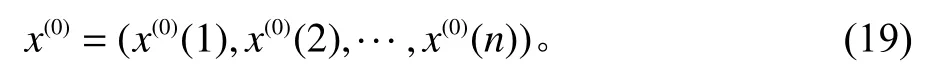
累加后生成的累加生成序列为

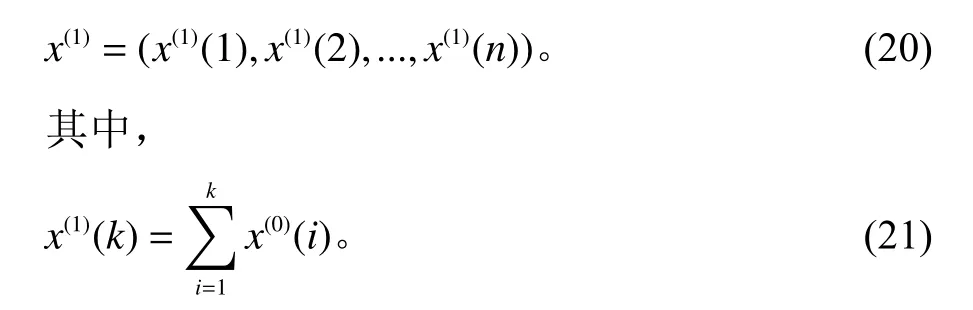
由累加生成序列建立累加生成线性微分方程

由方程(22) 可得累加生成序列的灰色预测值

其中，a、u为模型参量。

2.3 有效性分析

本文拟采用上述6个模型，进行可修航材预测。6个模型中，采用两个回归分析预测模型和3个时间序列预测模型。回归损失函数均方误差(mean squared error,MSE) 与函数平均绝对值误差(mean absolute error,MAE) 是回归分析中常用两个评价指标，两者都能计算出预测值误差，MSE能够提供良好性质的相似度的度量，求解方便且最优解唯一；MAE对于任意大小的差值其惩罚都是固定的，因此对于离群点不敏感。AIC(Akaike information criterion)信息准则常用于评价时间序列模型拟合数据的优良性，它基于熵的概念为模型的复杂性添加惩罚项来呈现随机变量的真实概率分布，从而解决了拟合过度的问题，使得数据的概率分布与估计概率分布相比熵的期望值最大[20]。AIC准则是基于拟合模型计算出残差的综合统计量来对模型进行比较的，而MSE与MAE更偏向于预测未来的发展趋势，注重预测的准确程度。3种评价方法结合能够避免其中一种方法的不足，提高预测的有效性，从而得出预测效果最优的方案。

MSE、MAE分别是对预测值和真实值之间差值平方进行求和与差值绝对值进行求和。其中，yi和分别为第i个真实观测值和预测值；n为观测值数目。

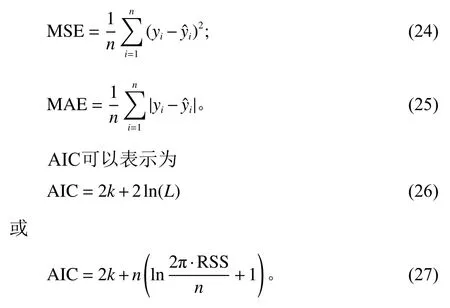
其中，k为模型中参数的数量；L为估计模型似然函数的最大值计算结果；RSS为残差平方和；n为观测值数目。

3 故障预测与结果分析

3.1 数据来源

根据空中客车公司提供的备件推荐清单(recommended spare part list，RSPL)，考虑到可修LRU件的维修技术性特征，按照以下条件进行筛选：SPC=2(Rotable周转件)，ESS=1(NO GO件)，25 000 h＜MTBUR＜35 000 h，LTM＜10(供应商管前置期)，QPA＞1(装机数) 。最终从中选择件号为3031863-001的发动机驱动泵(engine driver pump，EDP) 作为研究对象。

EDP是一类由发动机驱动的液压泵，它通过为飞机的各种操纵舵面、刹车和收放起落架等等提供液压动力来操作飞机的不同系统。EDP的单机装机数量为2，MST=15(平均在库维修时间)，单价UNP=35 549.28美元。

截至2019年12月31日，国内某航空公司A320系列飞机共有325架，其中经营租赁架数为124架，融资租赁、自购飞机架数分别为100架、101架(数据来源公司2020年报) 。如表2所示，观测期为2014年1月1日至2018年12月31日，共1 825 d。在这期间，该航空公司共有72架飞机出现EDP故障，其中34架为经营租赁，15架为融资租赁，29架是自有飞机；拆下EDP共计84个，故障飞机平均机龄为94个月，平均送修时间达到56 d。

表2 机队故障情况1)Table 2 Failure situation of fleet

根据EDP故障数据可以发现，其拆换需求具有明显的间歇性。2014～2018年的60个月中，有19个月无故障，占比31.6%，15个月只发生1次故障，占比25%，平均每月1.47个备件发生故障，具体数据如图1。

图1 故障数频数统计Figure 1 Frequency statistics chart of the number of failures

2014年与2016年故障数最多(见图2)，分别为22和25，在总共88个故障数中占到53%。

图2 年度故障数统计Figure 2 Annual failures statistics chart

按月度计算时，9、10月EDP故障数位居首位，3月与5月排在其后，具体数据见表3。

表3 月度故障统计Table 3 Failure situation of fleet per month

2014～2018年期间，该航空公司A320系列飞机机队EDP故障情况，如图3所示。

图32014 ～2018年EDP故障数据Figure 3 EDP failure data from 2014 to 2018

3.2 传统预测模型结果

根据前述数据，采集2014～2018年EDP的平均周转时间、MTBUR、单机年飞行小时等数据，计算出2019年推荐EDP采购数量，见表4。

表4 2019年推荐EDP采购数量Table 4 Recommended EDP procurement quantity in 2019

3.3 计量预测模型结果

通过数据分析，发现这些数据没有明显周期性变化的趋势，对其进行平稳性检验、基于差分法的数据平稳性处理，最后根据ACF和PACF图进行p、q阶数的判定，得到p=0，d=1，q=1的Arima(0,1,1)模型。

应用Python 3.8、Stata 16、Excel软件对预测模型进行建模，得到6个模型2014～2018年EDP故障数预测值，以半年为单位进行累计，故障累计图见图4。各种方法在AIC、MSE、MAE 3种准则下的预测精度见表5。

表5 几种不同方法的预测结果比较Table 5 Comparison of prediction results of different models

可以发现如下。

1) AIC准则下，模型精度排序为负二项回归＞GM(1,1) ＞ARIMA(p,d,q) ＞SBA＞Croston＞零膨胀回归。

MSE方法检验得出模型精度排序为GM(1,1) ＞负二项回归＞SBA＞Croston＞零膨胀回归＞ARIMA(p,d,q) 。

MAE方法检验得出模型精度排序为GM(1,1) ＞负二项回归＞Croston＞零膨胀回归＞SBA ＞ARIMA(p,d,q) 。

3个指标虽然结论有所差异，如图5所示。但负二项回归模型与GM(1,1) 在3种准则下预测精度相似，精度都高于其他模型。

图4 2014～2018年EDP故障数预测值Figure 4 The predicted value of EDP failures from 2014 to 2018

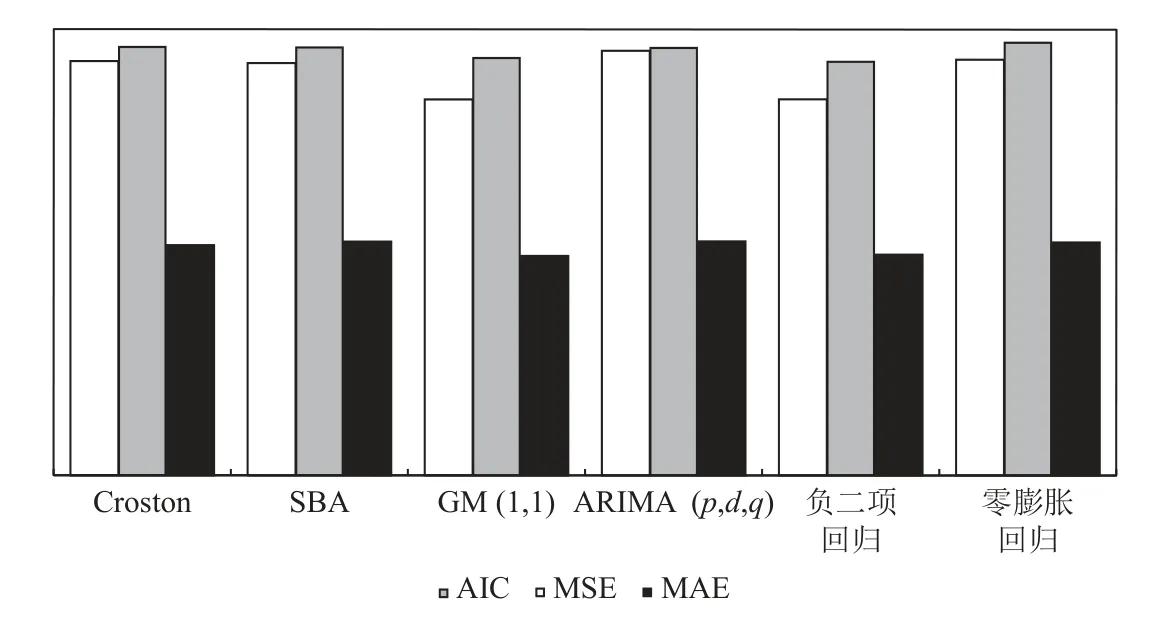
图5 3种准则下6种模型精度比较示意Figure 5 Comparison of models’ accuracy under three indexes

2) 应用6种模型对2018年、2019年的EDP故障总数进行预测，将预测值与真实值对比，结果如表6。由表6可知，负二项回归模型在所有模型中预测结果最接近真实值，GM(1,1) 预测误差尚可，但不如在3个准则下的模型精度表现突出。综上，6个模型中负二项回归模型效果更好。

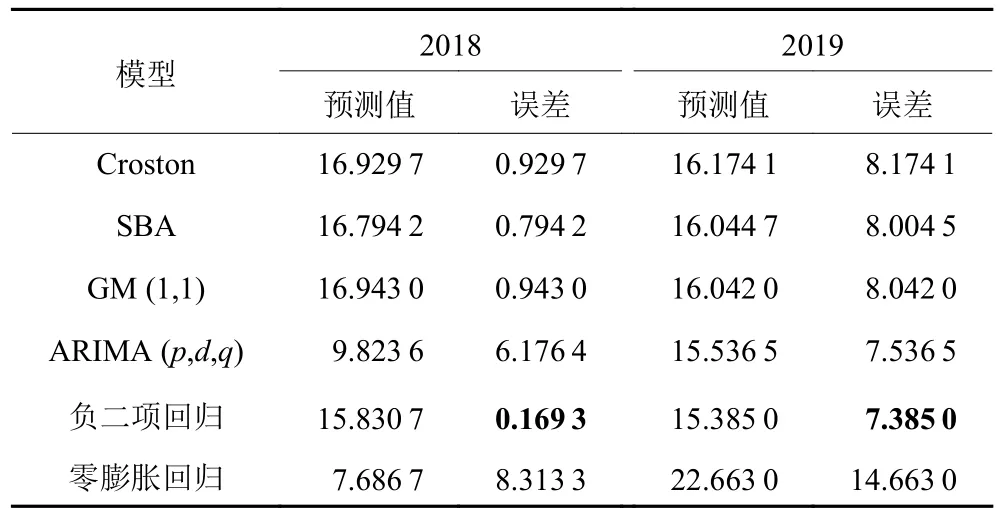
表6 2018年、2019年预测结果Table 6 Forecast results in 2018 and 2019

3) 特殊年份，传统预测模型与计量预测模型均无法获得较好的预测效果，有待改进。在2019年预测中，传统预测模型与计量预测模型中负二项回归模型都呈现出预测值偏高。根据表4可知，随着航班保障率要求增加，使用传统预测模型得到的预测值不断增大，与2019年实际运行的故障值之差从7件增长到9件。因此，即便按照传统预测模型中90%航班保障率要求的预测值进行的EDP需求采购，也可以满足2019年的实际运行，实际保障率可以达到100%。同时还存在约7件EDP闲置。负二项回归模型的预测结果也与之相同。根据EDP的购买价格，可得这7件闲置EDP的采购价格为248 844.96美元。而A320机队中，类似的ESS=2，价格在1万美元之上的航材超过500件，当出现类似EDP的冗余采购时，按照采购均价可得，对保障率没有贡献的冗余支出高达3亿美元。这说明，面对2019年的数据时，模型可能出现失效。

模型失效的原因可能是：1) 2019年故障真实值受到航空公司A320机队飞机机龄影响显著，而机龄因素在上述模型中均未考虑；2) 2019年向前追溯一个EDP的MTBUR时间，该航空公司的飞机维修能力可能得到大幅度的提升，使得现阶段在机运行的EDP件使用时长更长，2019年故障数明显减少。具体原因有待进一步探讨。此外，利用组合预测、系统建模和仿真方法或许会解决在特殊年份传统和单一预测模型失效的问题，仍有待进一步研究。

4 结论与展望

本文利用可修LRU件的故障次数拥有间歇性需求的特点，通过选择Croston模型、SBA模型与零膨胀回归模型来进行预测，尽量避免“0”取值过多而产生过度离散的结果。本文与文献[4]都选择了ARIMA(p,d,q) 模型与GM(1,1) 模型。相关研究已证实这两种方法适用于多种预测且都有较好的表现。除此之外，本文选择的负二项回归与文献[4]选择的泊松分布描述事件都为伯努利实验，但由于泊松分布需要其均值与方差相等，而负二项分布不同，它的方差随着均值的增加而以二次函数的形式递增，因此负二项回归更合适。通过算例对比，结论如下。

1) AIC准则更适合评价6种模型对LRU件需求预测。本文利用MSE、MAE、AIC信息准则对模型预测结果进行评价，主要权衡预测模型的复杂程度以及模型对数据的拟合程度。根据表5预测结果，与表6比较预测结果与实际值的误差值，可以发现AIC准则对于预测结果评价效果更优，可广泛应用于高价可修LRU需求预测效果判定。其原因可能是AIC考虑了模型的拟合情况与模型复杂度双重影响，采用在同等拟合优度条件下参数最少的模型作为估计模型，相比之下MSE、MAE更容易受到数据本身波动的影响，忽略异常值的影响。

2) 负二项回归模型优势明显。对2018年和2019年两年的预测中，负二项回归模型都表现较好，在6个计量预测模型中误差最小。同时分别与2018年和2019年使用传统预测模型得到的结果进行对比，可以发现，按照负二项回归模型的预测结果进行的航材采购，均可以满足航空公司航班保障率超过95%的要求。相对于传统预测模型，该模型作为计量预测模型在仅统计故障次数的情况下，可以实现预测，而不需要额外统计其他相关变量。

3) 算例数据来源有待多样性。现算例数据来源于某航空公司机队的EDP故障数据，数据相对单一，且来源不够多样化，未来研究可以尝试将多个公司、多个机组、不同来源的EDP故障数据进行对比分析，并加入更多的定性与定量讨论。

综上所述，本文选取常用的6种计量模型与航空公司传统预测模型，利用高价可修LRU件EDP的故障数据进行预测，通过有效性分析、真实值比较得出最优方案，即负二项回归模型。研究过程、所得结论和展望，均可为航空公司LRU件的维修及采购决策提供支撑。