考虑牛鞭效应的智慧供应链定价与投资决策研究

马卫民，孙小涵

(同济大学 经济与管理学院，上海 200092)

近年来，智慧供应链成为企业在新一轮发展浪潮中保持竞争力的关键。当前，众多企业对资源和需求的精准匹配要求越来越高，头部企业已经率先数字化转型。上汽通用五年前开始布局数字化，打造供应链一体化平台，结合数据进行预测分析，共享主机厂信息及策略等[1]。京东2017年对外发布智慧供应链战略，将技术创新和供应链创新相结合，形成智慧供应链解决方案[2]。同时，国内外学者也对此展开了深入研究。Ozer[3]指出，使用大数据可以帮助企业更加了解消费者的偏好和需求、在大量投资新产品之前作出更准确的销量预测和生产决策。Barton等[4]指出，决策者可以通过应用分析模型分析物联网数据以支持预测和优化结果。冉文学等[5]研究表明，应用区块链技术能降低供应链风险，提高供应链收益。

供应链管理中，需求信息和相关订单自下而上传递过程中扭曲放大的现象被称为牛鞭效应[6]，即实际消费者需求的微小变化会在供应链上游引发越来越大的振荡[7]。牛鞭效应导致了巨大的低效率、高风险和高成本，例如库存过多、客户服务差和收入损失等[8-9]。牛鞭效应的本质是信息在供应链传递中发生了偏差，而数字技术则可以有效缓解其负面影响。大数据有助于供应链企业精准预测市场需求并快速反应[10]。人工智能可以改进需求信号处理，减少供应链中的时间延迟[11]。云计算可以简化供应链内信息共享基础设施的提供，支持供应链内部和跨供应链的实时信息共享[12]。Wiedenmann等[13]对文献进行计量分析，确定了信息物理系统、云计算和人工智能是在牛鞭效应背景下最受关注的3种数字技术，并表明数字技术对牛鞭效应产生积极影响。杨礼凡[14]研究了在数字技术背景下供应链协调问题，结果表明采用数字技术可以弱化牛鞭效应。陈峰[15]指出大数据需求预测有助于提高供应链效率。诸多文献证实了数字技术可以减轻牛鞭效应并提高整体供应链绩效。

目前研究大多针对整个供应链的智慧化。事实上，京东、美团等大企业可以打造覆盖供应链从上游到下游的一体化平台、构建完整的智慧供应链，但更多的中小企业并不具备这种能力。中小企业为了长远发展可以选择投资数字技术进行自身技术升级，从而进行更准确的市场预测。因此，本文着眼于中小企业，基于供应链成员投资与否的不同情形建立以制造商和零售商为主体的博弈模型，并分析牛鞭效应对供应链最优定价、数字技术水平以及供应链成员利润的影响。

1 问题描述与假设

1.1 问题描述

本文研究由一个制造商和一个零售商组成的供应链。其中，零售商面临市场需求d，考虑到牛鞭效应对需求信息的逐级放大效果，零售商以其预测量q为 基础向制造商订购产品，且q＞d；制造商以零售商订货量为基础组织生产，生产量为Q，且Q＞q；产品的生产成本为c，批发价为w，零售价为p。由于智慧供应链以需求为导向，牛鞭效应是需求信息扭曲放大的结果，因此，本文假设掌握需求信息更多的一方作为Stackelberg博弈的领导者。

1.2 模型参数及符号说明

模型涉及的参数及其描述如表1所示。

表1 模型参数符号说明Table 1 Symbol description of parameters of model

为了探讨数字技术的作用，本文考虑以下4种情况(其中“I”“N”分别代表投资数字技术和不投资数字技术)：1)NN情况下，制造商和零售商都不投资，即普通供应链；2)II情况下，制造商和零售商都投资，即智慧供应链；3)IN情况下，只有制造商投资；4)NI情况下，只有零售商投资。

1.3 基本假设

1)市场需求受零售价影响，表示为关于零售价的线性函数，即d=a-bp；

2)智慧供应链数字技术投资成本被视为数字技术水平的二次函数，即

3)供应链上各主体的信息获取程度受数字技术水平θ影响，即θ 越大，各主体获取的信息越多；

4)本文只考虑正向的需求变化，不考虑需求减少的情况，即供应大于需求；

5)假设制造商和零售商均可以单独进行投资，从而提高数字技术水平，获取更多需求信息；

6)不考虑在期末尚未售出的产品残值。

2 模型的建立与分析

2.1 普通供应链(NN模型)

本文假设牛鞭效应导致需求放大的多少用决策方对信息的敏感程度(α、β)表示，敏感程度越高，受到的影响越大，因此，零售商的订购量是q1=d+α，制造商的生产量是Q1=q1+β。零售商、制造商的利润分别为

零售商作为供应链中更靠近市场的一方，同等条件下会比制造商掌握更多需求信息，因此在NN模型中，零售商作为博弈中的主导者，在博弈第一阶段决定零售价p1；制造商作为跟随者在观察到零售商决策后决定最优批发价w1。令p1=w1+x1，x1为单位产品利润。

命题1在NN模型中，制造商和零售商的最优决策分别为

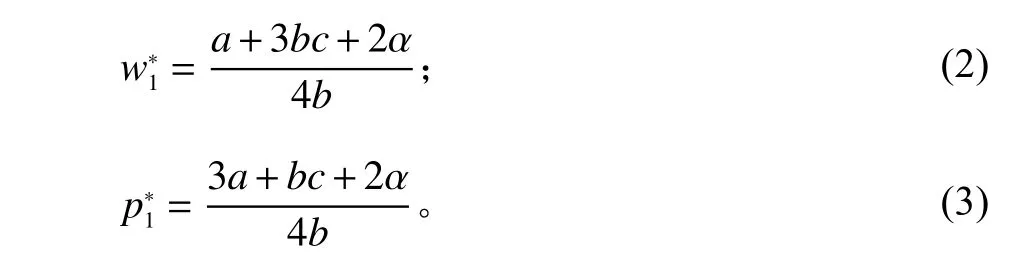
证明采用逆向归纳法求解。首先，制造商以自身利润最大化为目标进行决策，其最优决策结果可以通过一阶导数得到。

将w1代入零售商利润函数式(1)，然后求x1的一阶导数，并易证二阶导数小于0，πr1是关于x1的凹函数。令一阶导数为0，得到

2.2 智慧供应链(II模型)

更高水平的数字技术能够获取更多更准确的市场需求信息，从而在一定程度上抑制牛鞭效应。因此，假设零售商的订购量是q2=d+(1-kθ2)α，制造商的生产量是Q2=q2+(1-kθ2) β。零售商、制造商的利润为

同NN模型一样，零售商处于领导地位，决定零售价p2和数字技术水平 θ2；制造商作为跟随者决定批发价w2。

命题2在II模型中，当满足时，制造商和零售商的最优决策分别为

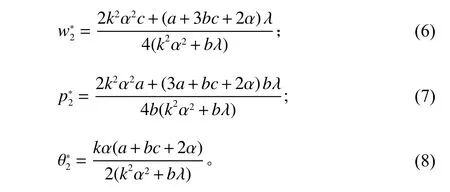
证明采用逆向归纳法求解。首先，易证πm2是关于w2的凹函数，令πm2关于w2的一阶导数等于0，得到

将式w2替换到式(5)中并化简，然后分别求πr2关于θ2、x2的一阶导数。

进而对θ2、x2求二阶导数可得海塞矩阵。

2.3 制造商单独投资数字技术(IN模型)

IN模型中，零售商凭经验预测市场需求信息，而制造商凭借大数据获取并预测市场需求信息。制造商作为获取信息更多更准确的一方成为博弈中的领导者，决定w3和 θ3，零售商成为跟随者，决定p3。因此，零售商的订购量是q3=d+α，制造商的生产量是Q3=q3+(1-kθ3) β。零售商、制造商的利润为

命题3在IN模型中，制造商和零售商的最优决策分别为

证明过程参考命题2。

2.4 零售商单独投资数字技术(NI模型)

零售商在已有经验的基础上通过大数据技术能够更精准地掌握市场需求信息，是供应链中的领导者，决定p4和 θ4，制造商是跟随者，决定w4。因此，零售商的订购量是q4=d+(1-kθ4)α，制造商的生产量是Q4=q4+β。零售商、制造商的利润为

命题4在NI模型中，当满足时，制造商和零售商的最优决策分别为

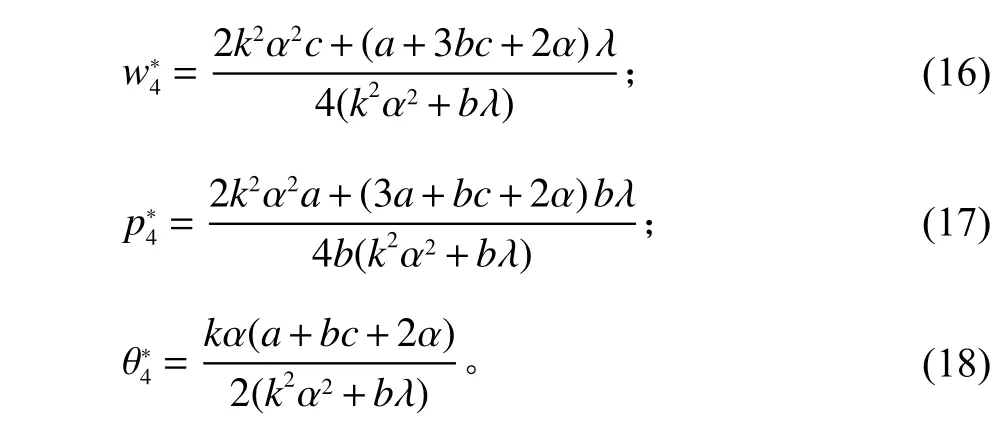
证明过程参考命题2。

2.5 均衡结果分析

推论1表明，定价决策仅受到零售商信息敏感度 α的影响。只有制造商单独投资数字技术的情况下，数字技术水平的决策结果会受到制造商对信息敏感度 β的影响，且数字技术水平与制造商、零售商对信息的敏感度正相关，即牛鞭效应影响较大时，供应链成员会设置更高的数字技术水平。

推论2表明，相较于普通供应链而言，制造商和零售商单独投资数字技术都会增加其本身获得的利润；而两者都投资数字技术时，零售商获得的利润与其单独投资持平，高于普通供应链和制造商单独投资时零售商获得利润。

推论3表明，IN模型和NI模型的供应链总利润高于NN模型，即制造商和零售商单独投资数字技术会提高整个供应链绩效。

3 数值算例

本节通过数值算例探讨牛鞭效应对不同情形下供应链利润的影响。相关参数设置如下：a=100，b=6，c=10，k=0.55，λ=200，α∈(0,20)，β∈(15,35)，其中α、β不同数值表示牛鞭效应对零售商、制造商产生的不同影响程度。

将上述参数代入4种模型并计算利润，然后均与普通供应链利润作比较。

图1展现了智慧供应链与普通供应链间的利润差，其中图(a)、(b)分别为β=20、α=10时的截面图。供应链整体的利润差值为正，且随着α、β的增加，利润差不断扩大；零售商的利润差值也为正，不受 β的影响，随着α 的增加而增长；制造商的利润差受到 β的正向影响，而随着α 的增加，利润差呈现先增后减的趋势。

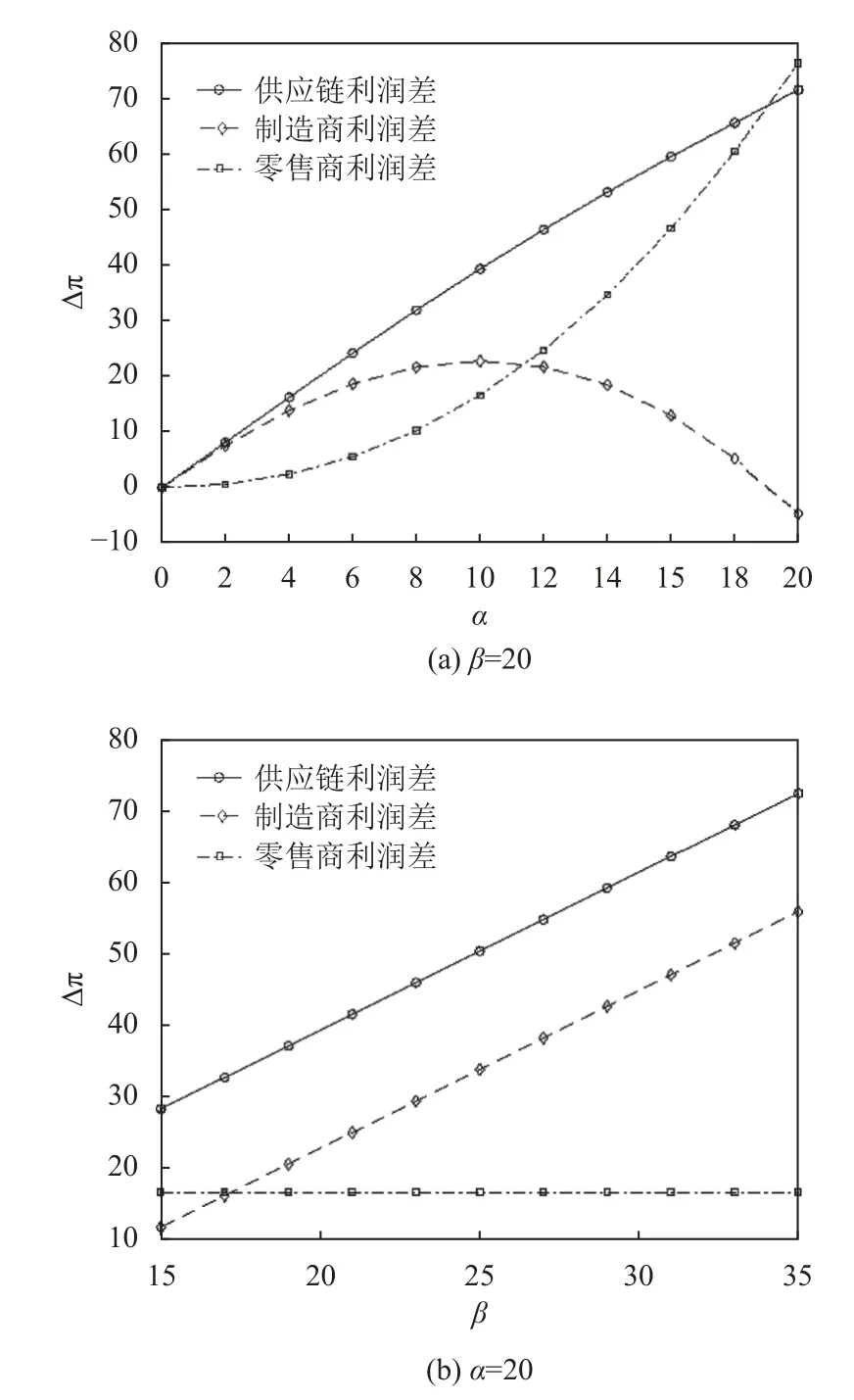
图1 牛鞭效应影响下的智慧供应链与普通供应链利润差Figure 1 The profit gap between the II model and the NN model under the influence of the bullwhip effect

相较普通供应链而言，智慧供应链的整体利润更多。α、β增加，最优数字技术水平提升，智慧供应链对牛鞭效应的抑制程度加大，产品订货数量和生产数量减少，投资成本增加。对于零售商而言，由提升数字水平所带来的订货成本的减少多于增加的投资成本，从而利润增加；而制造商利润减少的原因可能是投资成本过高，导致利润下降。

图2展现了制造商单独投资的供应链与普通供应链间的利润差。可以看到供应链整体的利润差值为正，不随 α变化，随着 β的增加利润差不断扩大；制造商的利润差值同样为正，随着α 与 β的增加而增长；零售商的利润差值始终为负，随着 α的增加差距不断扩大，不随 β变化。

图2 牛鞭效应影响下的制造商单独投资的供应链与普通供应链利润差Figure 2 The profit gap between the IN model and the NN model under the influence of the bullwhip effect

相较普通供应链而言，制造商单独投资数字技术使它本身的利润有所增长，而零售商所获利润减少，但供应链总绩效是增加的。

图3展现了零售商单独投资的供应链与普通供应链间的利润差。可以看出，零售商及整个供应链的利润差值均为正，制造商的利润差值为负，且均随着α 的增加差距不断扩大，而不受 β的影响。

图3 牛鞭效应影响下的零售商单独投资的供应链与普通供应链利润差Figure 3 The profit gap between the NI model and the NN model under the influence of the bullwhip effect

相较普通供应链而言，零售商单独投资数字技术使其本身利润有所增长，制造商所获利润降低，供应链总绩效增加。

4 结论

本文研究了由一个制造商和一个零售商组成的两级供应链，在考虑牛鞭效应的情况下，建立了供应链成员是否投资数字技术的4种不同情况的博弈模型，并分析了牛鞭效应对企业的定价决策和利润的影响。

结果表明，供应链成员会通过设置更高的数字技术水平来弱化牛鞭效应带来的影响；零售商单独投资数字技术时，能够提高其自身利润和供应链整体绩效；制造商单独投资时，能够使供应链中各方利润均有所提高；而两者同时投资时，却并不一定能获得更高的供应链利润。

本文对中小企业在智慧化供应链进程中的选择与决策具有借鉴意义。1)从零售商视角来看，只要供应链中有成员投资数字技术，都能够对其产生积极影响，但在两者均投资的情况下为了保证合作应限制数字技术水平，避免制造商因亏损而中断合作。2)从制造商视角出发，如果零售商不投资，制造商投资可以获得更多的利润；如果零售商投资，制造商投资与否都有可能会比现有情况更好，也可能所获利润会不如现状。3)从供应链整体视角来看，制造商或零售商单独投资都会产生积极影响，同时也有利于智慧供应链的发展。本研究存在一些局限性：本文中需求函数被认为是确定的，现实中更多的是不确定需求；在实际情况下，数字技术水平不是完全由主导方直接决定，本文的假设不完全符合实际中情况；本文考虑了具有两个成员的供应链，研究具有多个零售商或多个制造商的投资选择决策会更具挑战性。这些在后续研究中可以继续深化。