考虑权力结构与溢出效应的混合平台供应链定价决策研究

魏 杰，孟祥伽，徐泽灵

(河北工业大学 经济管理学院，天津 300401)

随着互联网的快速发展以及亚马逊、京东等平台商的迅速崛起，消费者从线下消费渠道逐渐向线上消费渠道转移。国家统计局数据显示，2020年全国社会消费品零售总额达39.2万亿元，其中线上零售额达11.76万亿元，同比增长10.9%。平台商的快速发展不仅为消费者带来了便捷的购物体验，同时也为制造商提供了商业机遇，大量拥有线下渠道的制造商开始通过平台商的电商平台进行线上销售。目前，制造商在电商平台上有两种典型的产品销售渠道：一是直销渠道，即平台商向制造商收取一定比例的佣金，并允许制造商在其电商平台上建立官方旗舰店直接销售产品；二是分销渠道，即平台商从制造商处批发产品，然后在其电商平台上建立自营旗舰店将产品销售给消费者。同一电商平台上也可以同时存在直销和分销混合销售渠道[1]。两种销售渠道的最大区别是定价主体不同，直销渠道中产品的零售价格由制造商决定，而分销渠道中产品的零售价格由平台商决定。

虽然制造商通过电商平台进行线上销售拓宽了产品的销售方式，但线上渠道的销售会影响线下渠道的销售。Yan等[2]和Abhishek等[3]认为，同品类/不同品类产品间线上到线下销售的溢出效应(简称“溢出效应”) 普遍存在，其溢出类型有正有负。正溢出效应指线上渠道销售增加线下渠道需求。负溢出效应指线上渠道销售侵蚀线下渠道需求。此外，实践中制造商和平台商之间存在不同的渠道权力结构，既存在制造商或平台商主导供应链的权力结构，也存在制造商和平台商权力相当的权力结构。例如，Chai等[4]指出，为了提高销量和品牌知名度，小型制造商愿意成为实力强大的平台商的追随者；为了成为限量版产品的独家代理机构，大型平台商愿意成为品牌制造商的追随者；在其他情况下，制造商和平台商可能具有相同的议价能力，任何一方都不能主导供应链决策。

不同的销售渠道会导致不同的零售价格决策者，进而影响制造商和平台商的利润，因此在基于电商平台的混合销售渠道下，研究制造商与平台商的定价决策及利润具有重要意义。此外，溢出效应的存在以及渠道成员间的权力结构差异也会影响制造商和平台商的定价决策及利润。那么，在上述3种权力结构下，制造商和平台商如何进行定价决策？与不存在溢出效应相比，溢出效应会如何影响定价决策？这些影响在不同权力结构下是否存在差异？制造商和平台商的利润在哪种权力结构下更大？以上都是未被研究且值得探讨的问题。

目前，关于电商平台销售渠道的研究主要集中在以下两个方面：其一，考虑制造商在电商平台存在单一销售渠道的情形。Yan等[2]考虑线上到线下销售的溢出效应，探讨制造商引入电商平台直销渠道的条件。Abhishek等[3]和李佩等[5]分别研究溢出效应和平台商引入自有品牌对平台商销售渠道选择的影响。田晨等[6]基于两个销售互补产品的制造商和一个平台商组成的供应链，研究制造商的销售渠道选择和平台商的物流服务决策。Ryan等[7]在零售商自建网络渠道存在情况下，研究其是否应该引入电商平台直销渠道以及如何进行定价决策。其二，考虑制造商在电商平台存在混合销售渠道的情形。Tian等[1]基于两个竞争制造商和一个平台商组成的供应链，研究平台商的销售渠道选择。王文宾等[8]探讨销售渠道对制造商和平台商定价决策及利润的影响。以上研究均是在制造商主导供应链情形下进行的，而本文研究的是制造商和平台商间权力结构存在差异的情形。

近年来，对于渠道成员权力结构的研究同样受到国内外学者的广泛关注，一些学者对制造商和零售商间权力结构进行了研究。孙书省等[9]基于线下权力结构差异，构建3种博弈模型，探讨线下权力结构与制造商线上销售模式之间的匹配关系。Liu等[10]针对不同权力结构下的定价时机进行研究，探讨其对渠道成员定价决策的影响。孙自来等[11]基于单个多渠道制造商和单个零售商组成的供应链，分析渠道成员间的权力结构对渠道成员定价、需求及利润的影响。Chen等[12]基于单个制造商和单个零售商组成的供应链，针对二者间不同权力结构研究制造商的最优批发价格、单位碳排放和零售商的最优零售价格决策。还有一些学者对制造商和平台商间权力结构进行了研究。Jia等[13]以制造商自建网络渠道和电商平台分销渠道组成的双渠道供应链为背景，研究权力结构对制造商和平台商定价及服务决策的影响。Chai等[4]基于O2O供应链，构建了制造商主导、平台商主导及权力相当3种博弈模型，分析权力结构对渠道成员利润的影响。不难发现，目前关于制造商和平台商间权力结构的研究较少，且未考虑制造商在电商平台存在混合销售渠道的情形。

对于溢出效应的研究，一些学者以制造商自建网络渠道为背景，研究了溢出效应对渠道成员定价决策及利润的影响。Pu等[14]发现在一定条件下，实体店服务水平和供应链总利润均随溢出效应的增加而下降。浦徐进等[15]研究溢出效应对双渠道供应链定价及零售商服务努力水平决策的影响。还有一些学者以制造商通过在线零售商进行线上销售为背景，研究溢出效应对渠道成员定价决策及利润的影响。Basak等[16]发现溢出效应会加剧传统零售商和在线零售商间的竞争，降低二者利润。Bing[17]指出在线零售商的退货政策可以缓解溢出效应对渠道成员定价决策的影响。以上研究均只考虑了负溢出效应，汪敢甫等[18]、马敬佩等[19]综合考虑了正、负溢出效应。上述关于溢出效应的研究均是在线下渠道和单一线上渠道并存的情况下进行的，未考虑线下渠道和多种线上渠道并存的情况。

综上可知，针对电商平台混合渠道的研究已经取得了一定成果，但已有研究未考虑制造商和平台商间权力结构存在差异的情况；此外，针对渠道权力结构和溢出效应的研究未考虑电商平台混合渠道存在的情况，且关于溢出效应的研究大多假设线上需求侵蚀线下需求，忽略了线上需求对线下需求有利的一面。基于此，本文考虑制造商通过电商平台混合渠道进行销售的实践背景，构建制造商主导供应链、平台商主导供应链以及制造商和平台商权力相当的决策模型，同时在3种权力结构下，分别给出存在和不存在溢出效应情形下制造商和平台商的最优定价决策及最大利润。

1 问题描述与假设

考虑一个拥有线下渠道的制造商和一个平台商组成的混合平台供应链，制造商负责生产产品，且所有产品通过线下渠道和平台商提供的线上渠道销售。具体来讲，存在分销渠道和直销渠道两种线上渠道。分销渠道中制造商以批发价格w将产品批发给平台商，平台商以零售价格p1将产品销售给消费者；直销渠道中制造商向平台商缴纳比例 λ的销售佣金，平台商允许制造商决策零售价格p2并直接将产品销售给消费者。实践数据表明，沃尔玛的佣金费率为6%～ 20%，亚马逊为1%～ 15%，京东为1%～ 10%，因此，本文假设0.01≤λ≤0.2。此外，假设制造商和平台商间需求信息及成本信息完全对称，且都是理性决策者，均以获取最大利润为决策唯一目标。

1.1 线上渠道

由于两种线上渠道的定价主体及定价策略不同，渠道间存在竞争。线上渠道间的竞争主要体现在线上零售价格。参考Tian等[1]和汪敢甫等[18]关于渠道竞争的研究，构建依赖于价格的线性需求函数模型，分销渠道和直销渠道的需求分别为

其中，下标1代表分销渠道；下标2代表直销渠道。类似于文献[18]，设分销渠道和直销渠道的潜在市场需求均为1。Di表示渠道i中产品的需求，i=1,2；pi表示渠道i中产品的零售价格，i=1,2 ；β(0＜β＜1)为交叉价格弹性系数，β越大，线上渠道间产品价格竞争强度越激烈。此外，类似于文献[1]和[9]，设产品生产成本及销售成本为零，这不影响本文的定性结论。

1.2 线下渠道

在线下渠道中，假设制造商以1元的单价销售产品，并且在没有线上渠道情况下基本需求为Q。考虑到实体店的推荐价格和运营因素，调整线下零售价格成本较高，参考文献[2]，假设线上销售并不影响线下渠道的价格。此外，类似于Abhishek等[3]的研究，考虑到线上销售对线下需求的影响，假设线上渠道存在时线下渠道需求为Q+µ(D1+D2)，其中 µ表示溢出效应，为便于计算及保证各销售渠道需求和利润非负，µ的取值满足-0.5≤µ≤0.5，供应链结构如图1所示。

图1 线上销售到线下销售的溢出效应Figure 1 Spillover effects of online to offline sales

当µ=0时，表示不存在溢出效应；当µ＜0时，溢出效应为负，线上渠道每出售一单位的产品将导致线下渠道销售额减少 µ单位。这种消极影响在实际中广泛存在，特别是对于短期内不会再次购买的耐用品。在这种情况下，消费者一旦在网上购买了某产品，就不太可能去实体店购买该产品或其替代品[2]；当µ＞0时，溢出效应为正，线上渠道每出售一单位的产品将导致线下渠道销售额增加 µ单位。这种积极影响往往来自于口碑传播，特别是对于口碑良好的消耗品。

2 模型构建

为便于描述，用M、V、E分别表示制造商主导供应链、制造商和平台商权力相当及平台商主导供应链；用N、S分别表示不存在及存在溢出效应。不存在溢出效应时制造商、平台商和供应链的利润函数分别为

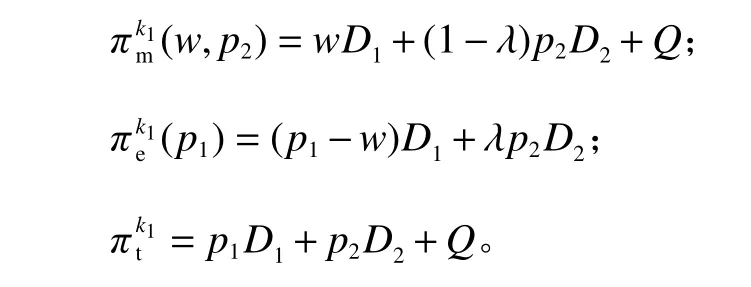
存在溢出效应时制造商、平台商和供应链的利润函数分别为

2.1 制造商主导供应链且不存在溢出效应(MN)

MN情形下，制造商作为Stackelberg博弈的主导者，平台商作为追随者。博弈顺序为：首先制造商决策零售价格p2和批发价格w，然后平台商决策零售价格p1。MN情形下的决策模型如下。

命题1MN情形下，产品的最优零售价格及最优批发价格分别为

2.2 制造商和平台商权力相当且不存在溢出效应(VN)

VN情形下，制造商与平台商进行Nash博弈。制造商决策零售价格p2和批发价格w的同时平台商决策零售价格p1。VN情形下的决策模型如下。

命题2VN情形下，产品的最优零售价格及最优批发价格分别为

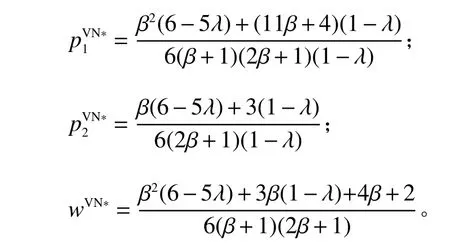
证明设p1=w+m(m＞0)，m为平台商获得的边际利润。求得(w,p2)关于w和p2的Hessian矩阵为

2.3 平台商主导供应链且不存在溢出效应(EN)

EN情形下，平台商作为Stackelberg博弈的主导者，制造商作为追随者。博弈顺序为：首先平台商决策零售价格p1，然后制造商决策零售价格p2和批发价格w。EN情形下的决策模型如下。

命题3EN情形下，产品的最优零售价格及最优批发价格分别为

证明设p1=w+m(m＞0)。首先求得(w,p2)关于w和p2的Hessian矩阵

2.4 制造商主导供应链且存在溢出效应(MS)

MS情形下的决策顺序同MN情形，MS情形下的决策模型如下。

命题4MS情形下，产品的最优零售价格及最优批发价格分别为

证明过程与命题1的证明过程类似，不再赘述。

2.5 制造商和平台商权力相当且存在溢出效应(VS)

VS情形下的决策顺序同VN情形，VS情形下的决策模型如下。

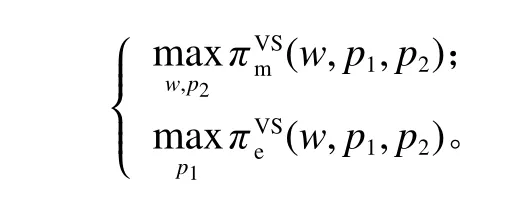
命题5VS情形下，产品的最优零售价格及最优批发价格分别为

证明过程与命题2的证明过程类似，不再赘述。

2.6 平台商主导供应链且存在溢出效应(ES)

ES情形下的决策顺序同EN情形，ES情形下的决策模型如下。

命题6ES情形下，产品的最优零售价格及最优批发价格分别为

其中，A2=(14β2+32β+12)λ2-(30β2+64β+24)λ+16(β+1)2-4。

证明过程与命题3的证明过程类似，不再赘述。

3 模型结果分析

3.1 溢出效应对均衡解的影响

由性质1可知，产品的最优批发价格和最优零售价格均随正溢出效应的增强而降低，随负溢出效应的增强而升高，该结论不依赖渠道成员间的权力结构。这是因为当溢出效应为正时，线上需求刺激线下需求，因此制造商会降低产品的零售价格以扩大线上需求，形成规模经济效益，同时降低产品的批发价格，激励平台商降低产品的零售价格来吸引更多消费者；当溢出效应为负时，线上需求侵蚀线下需求，因此制造商和平台商会提高产品的批发价格和零售价格以减少线上需求，避免线下需求被过度侵蚀。这表明，当溢出效应为正时(如口碑良好的消耗品)，制造商和平台商均可以设定较低的零售价格；当溢出效应为负时(如短期内不会再次购买的耐用品)，制造商和平台商均可以设定较高的零售价格。

3.2 权力结构对均衡解的影响

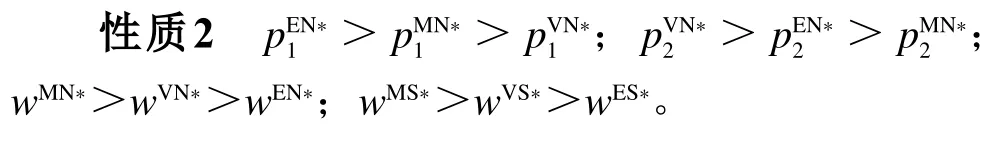
由性质2可知，不存在溢出效应时，分销和直销渠道中产品的最优零售价格受制造商和平台商间权力结构的影响。具体来讲，平台商主导供应链时，分销和直销渠道中产品的最优零售价格高于制造商主导供应链时的最优零售价格，这表明，当制造商和平台商权力不对等且制造商处于强势地位时，购买分销/直销渠道产品的消费者的收益增加。此外，无论是否存在溢出效应，产品的最优批发价格均随制造商主导地位的下降而逐渐降低。这是因为在制造商主导供应链时，制造商拥有较大竞争优势，将最大程度地提高批发价格；在平台商主导供应链时，平台商为了获得最大利润，在价格博弈中会极力压低批发价格。

由性质3可知，不存在溢出效应时，制造商和平台商均在自身主导供应链时获得最大利润，在对方主导供应链时获得最小利润。从整个供应链角度来看，供应链的总利润在制造商和平台商权力相当时最大。这意味着渠道成员具有对等的权力结构比不对等的权力结构更能增加供应链的总利润。

3.3 佣金费率对均衡解的影响

由性质4可知，在制造商主导供应链情形下，产品的最优批发价格随佣金费率的增加而降低，该结论与溢出效应无关。不存在溢出效应时，产品的最优零售价格不受佣金费率的影响；溢出效应为负时(如短期内不会再次购买的耐用品)，产品的最优零售价格随佣金费率的增加而升高；溢出效应为正时(如口碑良好的消耗品)，产品的最优零售价格随佣金费率的增加而降低。

证明过程与性质4的证明过程类似，不再赘述。

由性质5可知，在制造商和平台商权力相当时，产品的最优批发价格随佣金费率的增加而降低，该结论与溢出效应无关。溢出效应为负/不存在溢出效应/正溢出效应较小时，产品的最优零售价格随佣金费率的增加而升高；正溢出效应较大时，产品的最优零售价格随佣金费率的增加而降低。此外，不存在溢出效应/溢出效应为正时，产品的最优零售价格随佣金费率的变化趋势与性质4中变化趋势不同，这表明，渠道成员间的权力结构影响产品的最优零售价格随佣金费率的变化趋势。

性质4和性质5的分析表明，溢出效应仅影响产品的最优零售价格随佣金费率的变化趋势而不影响产品的最优批发价格随佣金费率的变化趋势。

4 数值分析

由于上述模型的均衡解比较复杂，本节采用Matlab软件进行数值仿真，进一步分析溢出效应及佣金费率对渠道成员定价决策及利润的影响。参数取值借鉴文献[2-3,9]。

4.1 溢出效应对最优零售价格的影响

设µ∈[-0.5，0.5]，其他参数设置如下：λ=0.1，β=0.4，Q=1，结果见图2和图3。

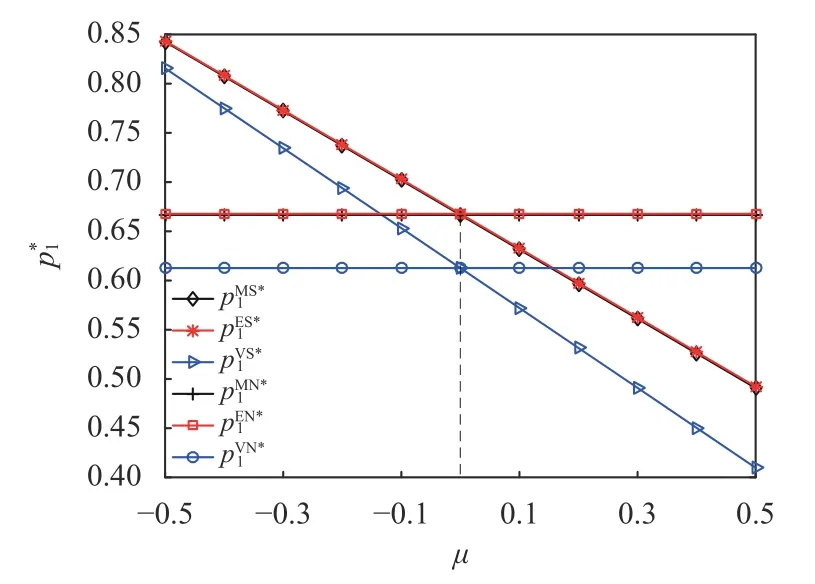
图2 分销渠道中最优零售价格随 µ的变化情况Figure 2 Changes of optimal retail prices with µ in the distribution channel

图3 直销渠道中最优零售价格随µ的变化情况Figure 3 Changes of optimal retail prices with µ in the direct selling channel

由图2可知，随着负溢出效应的减弱或正溢出效应的增强，分销渠道中产品的最优零售价格降低，该结论不依赖渠道成员间的权力结构。这表明，当正(负) 溢出效应较大时，制造商可以设定更低(高) 的分销渠道零售价格；当正(负) 溢出效应较小时，分销渠道零售价格降低(提高) 的空间较小。此外，分销渠道中产品的最优零售价格在平台商主导供应链时最高，在制造商主导供应链时次之，在二者权力相当时最低，其在不同权力结构下的差值随负溢出效应的增强而减小，随正溢出效应的增强而增大。这表明，负溢出效应减弱了权力结构对分销渠道中产品的最优零售价格的影响，而正溢出效应增强了权力结构对分销渠道中产品的最优零售价格的影响。

由图3可知，随着负溢出效应的减弱或正溢出效应的增强，直销渠道中产品的最优零售价格降低，该结论不依赖渠道成员间的权力结构。这表明，当正(负) 溢出效应较大时，平台商可以设定更低(高) 的直销渠道零售价格；当正(负) 溢出效应较小时，直销渠道零售价格降低(提高) 的空间较小。此外，直销渠道中产品的最优零售价格在二者权力相当时最高，在平台商主导供应链时次之，在制造商主导供应链时最低，其在不同权力结构下的差值随负溢出效应的增强而减小，随正溢出效应的增强而增大。这表明，负溢出效应减弱了权力结构对直销渠道中产品的最优零售价格的影响，而正溢出效应增强了权力结构对直销渠道中产品的最优零售价格的影响。

由图2和图3可知，无论渠道成员权力结构如何，随着负溢出效应的减弱或正溢出效应的增强，直销及分销渠道中产品的最优零售价格变化程度不同，具体来说，直销渠道中产品的最优零售价格降低得更快。这表明，直销渠道中产品的最优零售价格对 µ的敏感性大于分销渠道中产品的最优零售价格对 µ的敏感性。此外，分销渠道中产品的最优零售价格始终高于直销渠道中产品的最优零售价格，消费者更愿意购买制造商通过直销渠道销售的产品。

4.2 溢出效应对渠道成员利润的影响

设µ∈[-0.5，0.5]，其他参数设置如下：λ=0.1，β=0.4，Q=1，结果见图4。

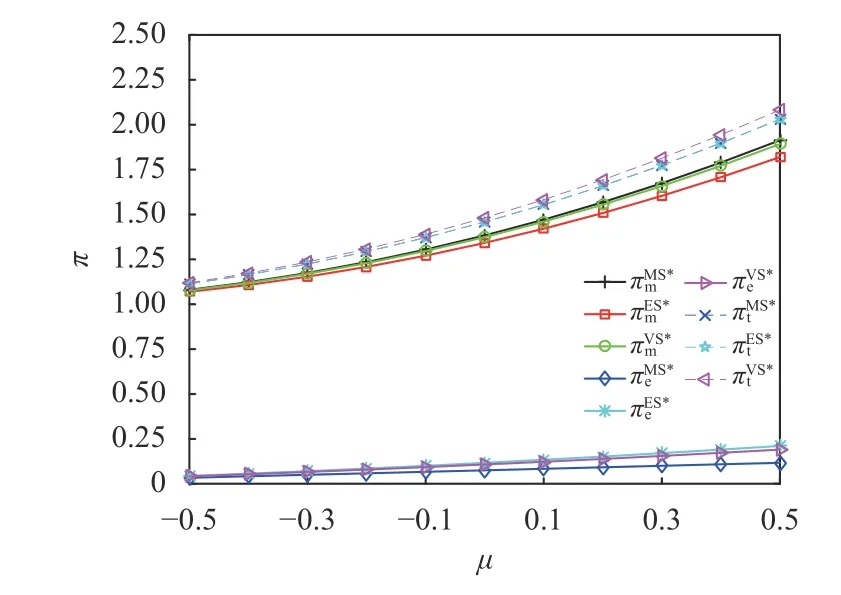
图4 渠道成员利润随µ的变化情况Figure 4 Changes of channel members' profits with µ

由图4可知，随着负溢出效应的减弱或正溢出效应的增强，制造商和平台商的利润均增加，且制造商的利润增加较快。这表明，相比于平台商，制造商对溢出效应的变化更加敏感。此外，供应链的总利润在制造商和平台商主导时基本相等，且小于权力相当时的总利润，这意味着从最大化供应链总利润角度来说，权力对等的结构比权力不对等的结构更有优势。

4.3 佣金费率对渠道成员利润的影响

通过性质4和性质5的分析发现，不存在及存在溢出效应时，佣金费率对产品最优零售价格的影响不同，因此本小节分析不存在及存在溢出效应两种情况。设λ∈[0.01，0.2]，分别取µ=0和µ=0.2，其他参数设置如下：β=0.4，Q=1，结果见图5和图6。

图5 µ=0时渠道成员利润随λ的变化情况Figure 5 Changes of supply chain members' profits with λ when µ=0

图6 µ ≠ 0时渠道成员利润随λ的变化情况Figure 6 Changes of channel members' profits with λ when µ ≠ 0

由图5和图6可知，无论是否存在溢出效应，制造商的利润均随佣金费率的增加而减少，平台商的利润均随佣金费率的增加而增加。这是因为佣金费率实质上是制造商和平台商的利润分配比例，佣金费率越高，制造商获得的利润份额越低，平台商获得的利润越高。与不存在溢出效应相比，存在溢出效应时制造商和平台商的利润随佣金费率的变化趋势较缓慢。这表明，溢出效应减弱了佣金费率对制造商和平台商利润的影响程度。此外，无论是否存在溢出效应，制造商和平台商均在作为供应链主导者时获得最大利润，在作为供应链追随者时获得最小利润。这一分析表明，对制造商和平台商而言，在不同权力结构中占据主导地位者可获得更多的利润。

5 结论

本文基于一个通过线下渠道和电商平台混合渠道销售产品的制造商和一个平台商组成的混合平台供应链，考虑3种权力结构(制造商主导/平台商主导/权力相当) 以及两种溢出效应(正溢出/负溢出)，运用博弈论建立6个决策模型，对比分析各模型下渠道成员的定价决策及利润，以期为混合渠道中产品定价和销售提供理论指导。研究发现如下。1) 随着负溢出效应的减弱或正溢出效应的增强，混合渠道中产品的零售价格降低，制造商和平台商的利润增加，该结论与渠道成员间权力结构无关。由此可知，制造商和平台商应根据溢出效应适当调整产品零售价格，协调线上线下渠道需求，以获取更大利润。2) 平台商主导供应链时，混合渠道中产品的零售价格高于制造商主导供应链时的零售价格，其在不同权力结构下的差值随负溢出效应的增强而减小，随正溢出效应的增强而增大。3) 无论是否存在溢出效应，制造商和平台商的自身渠道权力显著影响其利润，掌握供应链的主导权有利于提升自身利润，供应链的总利润在制造商和平台商权力相当时最大。由此可知，渠道成员具有对等的权力结构比不对等的权力结构更能增加供应链的总利润。

本文仅考虑了线下渠道零售价格外生的情形，进一步研究可以考虑将线下渠道零售价格设置为内生变量，对比分析渠道成员的定价决策及利润。