考虑综合收益最大的低压配电网三相不平衡治理模型研究
张明明,秦平,陈永进,贾恒杰,王兆健
(1.广东电网有限责任公司韶关供电局,广东 韶关 512026;2.广州市奔流电力科技有限公司,广州 510670)
0 引言
在我国,单个低压配电变压器(以下简称“配变”)及其供电区域通常被称为配电台区。目前的配电台区一般采用三相四线制的供电方式,用电形式以单相用户为主、三相用户并存[1]。台区单、三相负荷混合接入,单相表的接入往往没有充分考虑负荷的三相均衡,而且,用户用电行为在时间上具有随机性,使三相电流不平衡长期普遍存在。三相不平衡对低压配电网的供电质量、经济运行都将产生不利影响,较为明显的包括:配变损耗增大、线损增大等[2-5]。同时,因三相不平衡造成台区末段电压偏低也会进一步增大线损,这在农村远距离供电地区较为突出。因此,研究配电台区三相不平衡治理模型,通过降低三相不平衡来进行节能降损,不仅能提高用户用电质量,还有助于提高电网公司的运行效率效益[6-7]。
当前解决三相不平衡的方式主要有负荷补偿和相序调整[8-11],前者通过在线路首端相间跨接电容器来平衡安装点前段电流,可使三相电流平衡,但无法调节安装点后的负荷;后者通过换相装置或人工调相实现负荷在台区的均衡分布,是从源头上解决三相电流不平衡的有效方式。在三相不平衡治理模型的研究中,文献[12-15]分别采用以不平衡度最小、换相次数最少或两者相结合的策略作为模型目标,较少从实际工程角度考虑在允许的三相不平衡范围内综合收益的提升程度。在综合收益的评价中,节能降损效益的计算是重点。其中,配变降损效益可以结合序阻抗的方法较为准确地量化[16-21];而线路损耗的计算存在着现实的困难,主要原因在于配电台区物理拓扑和网架参数未知。虽然已有许多文献对三相不平衡引起的线损进行了推导[22-25],但鲜有文献考虑低压配电线路电阻的获取方式,导致这些方法都难以实际应用。
基于上述背景,本文提出一种考虑综合收益最大的低压配电网三相不平衡治理模型,求解模型后获取台区单相表的相序调整方案,从经济层面提供三相不平衡治理决策。首先,分析三相不平衡对台区损耗的影响,结合当前台区所能获取的数据,提出实用化的线路损耗以及配变损耗的量化方法;其次,建立以综合收益最大为目标的优化数学模型,模型中折算了相序调整后线路损耗、配变损耗降低所带来的收益和相序调整时产生的成本;最后,采用遗传算法求解仿真算例,获取相序调整方案,验证了本文所提模型的优势。
1 台区损耗实用化计算方法
1.1 三相不平衡下的台区线路损耗计算
对于三相四线制的低压网架结构,如果三相电流平衡,损耗只会发生在相线上;而对于三相不平衡情况,其产生的零序电流还会导致零线上的损耗增加,当零线的线径较小时,损耗更为明显[26-30]。为评估线路损耗并应用于指导相序调整,本文结合台区现有的量测数据,采用配变低压侧各相电流和有功损耗分别采用最小二乘法拟合对应相的等值电阻,通过对应相上的等值电阻和经相序调整后的电流便可以近似获得台区相序调整后的有功损耗。具体的推导如下文所述。
首先,β相上的等值电阻Rβ拟合公式为
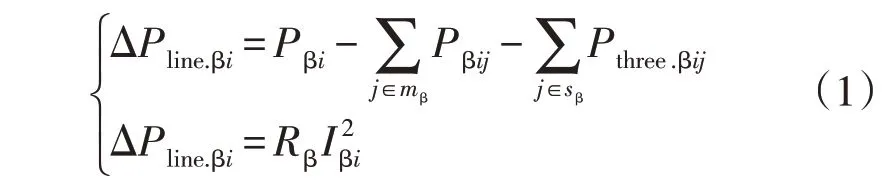
式中:ΔPline.βi为第i个采样点β相的总有功损耗;Pβi为配变低压侧第i个采样点β相的有功功率;Pβij、Pthree.βij分别为β相上单、三相用户j在第i个采样点的有功功率;Iβi为配变低压侧第i个采样点β相的电流;mβ、sβ分别表示相序调整前β相单、三相表用户的编号集合,β=A,B,C。
设共有n个采样点,根据最小二乘法,Rβ的计算公式为
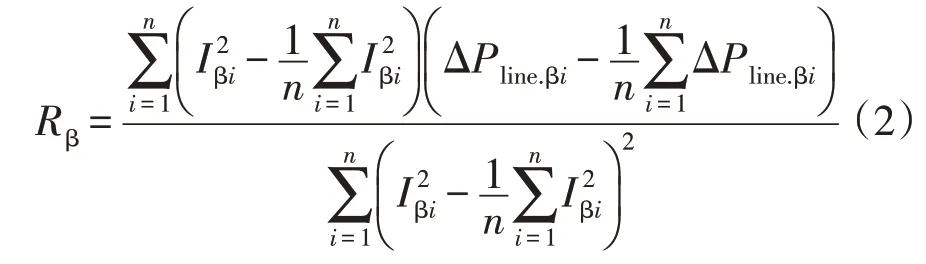
相序调整后,配变低压侧负荷发生变化,配电台区线路有功损耗计算公式为
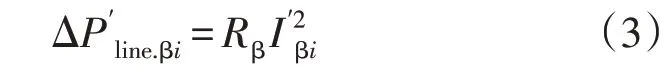
需要指出的是,以上过程是针对相线而言的。对于零线,式(1)中的有功损耗由台区总损耗减去各相损耗得到,式(3)中电流由各相电流求剩余电流得到。
1.2 三相不平衡下的配变损耗计算
配变损耗包括空载损耗和负载损耗,前者由变压器空载运行产生,不受三相不平衡影响,后者的损耗大小取决于负载运行情况。因此,三相电流不平衡主要影响负载损耗。为方便核算不平衡对配变负载损耗的影响,将变压器低压侧三相电流转换为序分量,并计算序分量分别在配变对应序阻抗上产生的损耗。
配变的序阻抗受不同接线方式的影响,本文以当前电力系统中使用比较普遍的Dyn11 联结的配变为例,配变正序等值电阻基本等于短路电阻,负序等值电阻与正序等值电阻一致,零序等值电阻一般通过实验测得。因此,正序电流在配变正序等值电阻上产生的有功损耗公式为
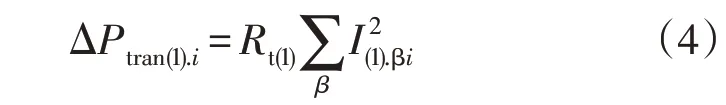
式中:ΔPtran(1).i为第i个采样点正序电流在配变中产生的损耗;Rt(1)为配变正序等值电阻;I(1).βi为配变低压侧第i个采样点β相正序电流。
负序电流在配变负序等值电阻上产生的损耗公式为

式中:ΔPtran(2).i为第i个采样点负序电流在配变中产生的损耗;Rt(2)为配变负序等值电阻;I(2).βi为配变低压侧第i个采样点β相负序电流。
零序电流在配变零序等值电阻上产生的损耗公式为
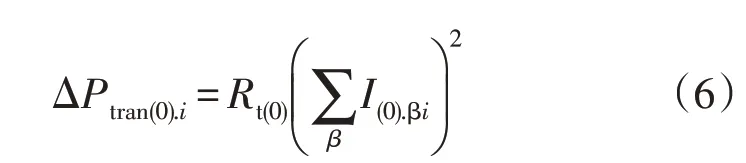
式中:ΔPtran(0).i为第i个采样点零序电流在配变中产生的损耗,Rt(0)为配变零序等值电阻;I(0).βi为配变低压侧第i个采样点β相零序电流。
因此,在不同时刻下,配变受负载变化的影响所对应的负载损耗ΔPtran.i公式为
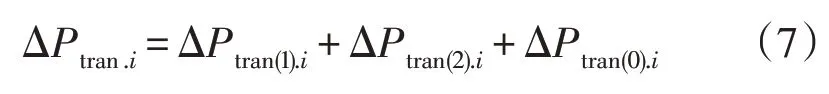
2 三相不平衡治理数学模型
本文通过调整单相表相序以实现三相不平衡的治理,在这一过程中可降低台区线路及配变损耗。经上文对线路损耗和配变损耗的推导,可建立以综合收益最大为目标的数学模型,获取对应的单相表相序调整方案。其中,综合收益的计算需考虑相序调整后,配电台区线路损耗及配变损耗降低带来的收益、调整相序时所产生的人力成本。
假设Xj、Yj、Zj分别是相序调整前A、B、C 三相上单相用户j的目标相序,表示原A 相用户j的相序保持不变;Xj=[0,1,0]表示原A 相用户j的相序调整到B 相;Xj=[0,0,1]表示原A 相用户j的相序调整到C 相,Yj、Zj同理。
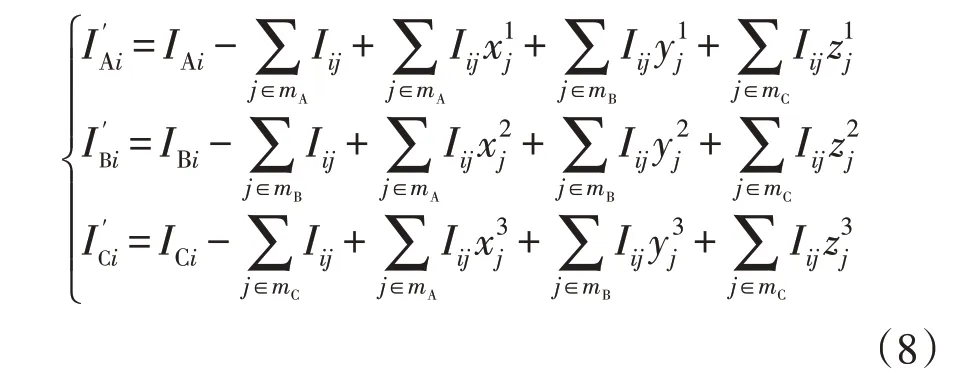
式中:IAi、IBi、ICi和分别为相序调整前、后配变低压侧第i个采样点A、B、C 相的电流;Iij为用户j在第i个采样点的电流;mA、mB、mC为相序调整前A、B、C 相单相表用户的编号集合。
1)线路损耗降低所产生的收益C1。
线路损耗降低所产生的收益C1公式为
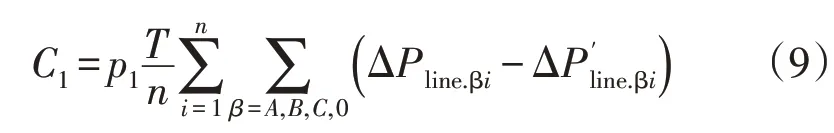
式中:p1为单位电价;T为相序调整周期。
2)配变损耗降低所产生的收益C2。
配变损耗降低所产生的收益C2公式为
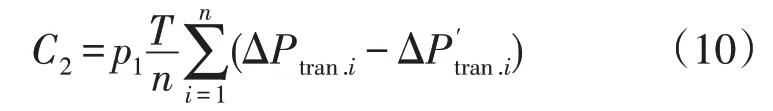
3)相序调整产生的人力成本C3。
相序调整产生的人力成本C3公式为

式中:p2为单相表调整所需单价;K为单相表调整个数。
综上,考虑综合收益最大化的三相不平衡治理模型公式为
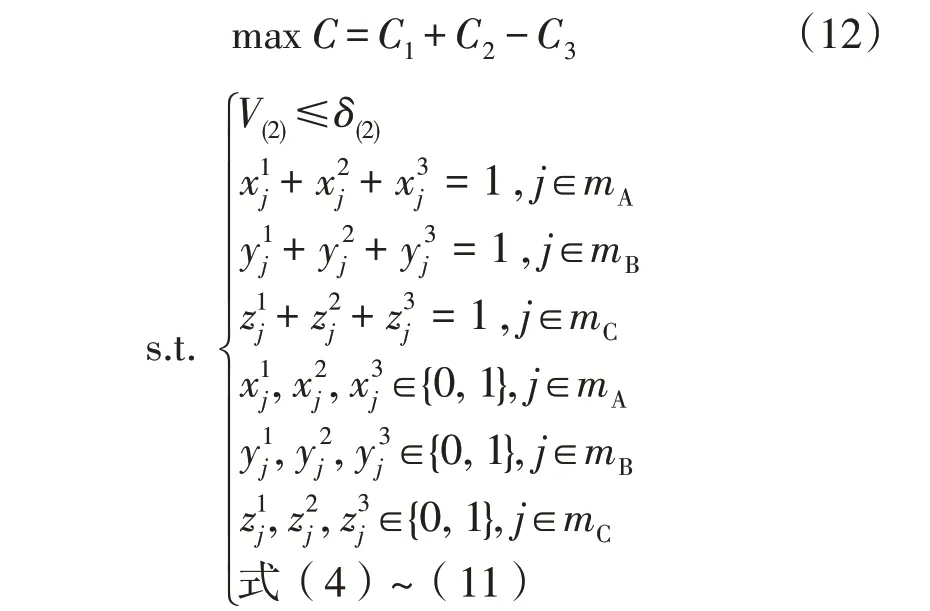
式中:V(2)表示配变低压侧负序电压;δ(2)表示最大允许的负序电压,按标准设为2%[26]。负序电压通过负序阻抗和负序电流计算获得。
3 仿真算例
选取某个实际台区,将其网架结构和实际运行数据用于仿真计算,验证所提模型的效果。算例的参数见表1。该配电台区下辖70 个单相用户,配变容量为100 kVA,空载损耗为290 W,负载损耗为1 500 W,空载电流百分数为1.6%,短路电压百分数为4%,配变低压侧的三相电流曲线如图1 所示。
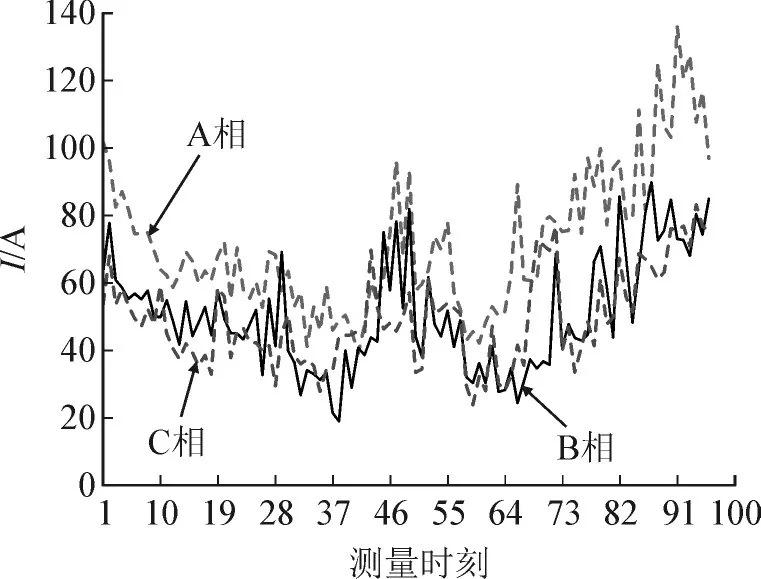
图1 相序调整前配变低压侧三相电流曲线Fig.1 Curve of three phase current at low voltage side of distribution transformer before phase sequence adjustment
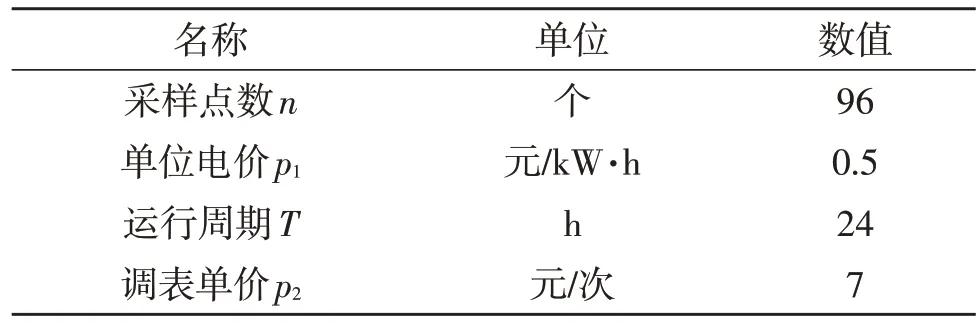
表1 仿真算例参数Table 1 Parameters of simulation example
选取典型日的负荷数据,每个季度对相序进行一次调整,建立综合收益最大模型后,采用Matlab遗传算法工具箱求解获得相序调整方案。根据所提模型方案调整后,可将平均三相不平衡度从36.86%降低至17.08%,降低幅度达到53.66%,整个季度可获得的综合收益为299.54 元。方案调整前后的配变低压侧不平衡度曲线如图2 所示,有效降低了最大不平衡度的幅值和台区整体不平衡度的水平。
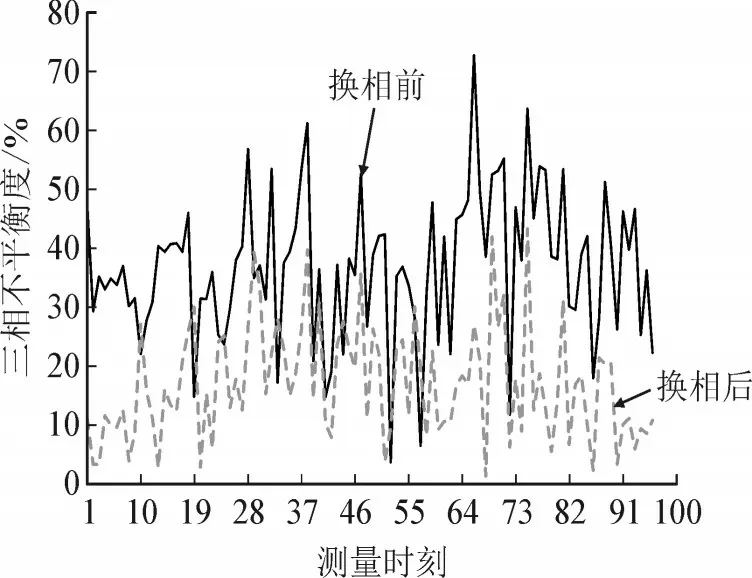
图2 相序调整前后配变低压侧三相电流不平衡度Fig.2 Three phase unbalanced current at low voltage side of distribution transformer before and after phase sequence adjustment
同时,通过相序调整前配变低压侧的各相电流和对应相的有功损耗,可拟合出等值电阻,进一步获得相序调整后的线路有功损耗,如图3 所示。
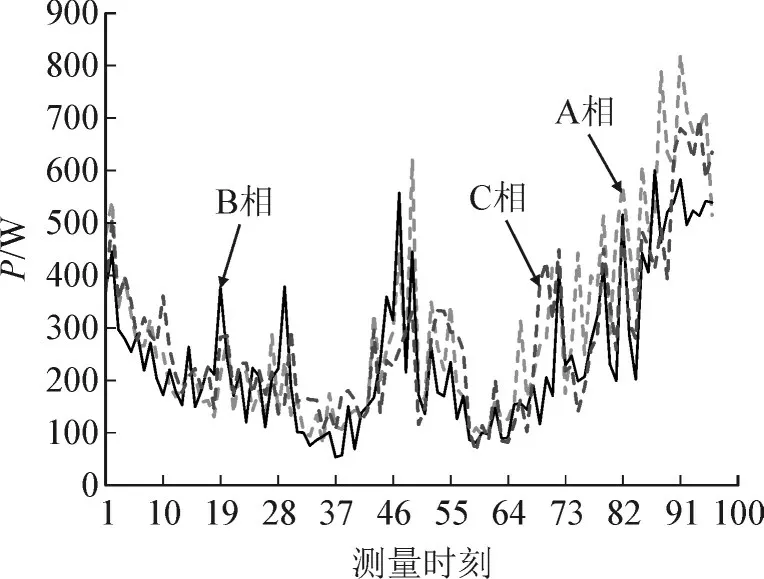
图3 相序调整后三相线路有功损耗曲线Fig.3 Active power loss curve of three phase line afteradjustment of phase sequence
作为对比,在同样的条件下,求解以平均不平衡度最小为目标的模型。经该模型方案调整后,平均三相不平衡度可降低至14.97%,综合收益为203.37 元。与本文所提模型相对比,虽然电流不平衡度降低了2.11%,但采用本文所提方法,三相不平衡度已满足标准要求,在此前提下追求三相不平衡度最低的效益并不明显;本文所提模型的综合效益是该模型的1.47 倍,效益有显著的提升。
对某地市供电所进行测算,该供电所下辖159 个配电台区,配变总容量为38 920 kVA,三相电流不平衡度大于30% 的台区约占65%。若该部分台区三相不平衡均采用本文所提方法完成治理,用本算例的单位容量收益进行折算,该所全年可获得的综合收益约为30.31 万元,规模效益相当显著。
4 结语
本文以低压配电网为研究对象,分析了三相不平衡治理的综合效益,提出了兼顾质量与效益的低压配电网三相不平衡治理模型,具体结论如下:
1)针对当前配电台区存在突出的三相电流不平衡问题,提出了一种考虑综合收益最大的低压配电网三相不平衡治理模型,可有效获取台区单相表的相序调整方案。
2)在模型建立过程中,针对配电台区线路损耗较难估算的问题,提出了一种适用于三相不平衡情况下的台区线路损耗计算方法,量化了相序调整后的台区线路损耗。
3)与平均三相不平衡度最小为目标的模型对比,本文所提模型产生的经济效益更明显,适合电网公司在配电台区三相不平衡治理上的工程化应用和推广。

