直流滤波电容器心子振动机理及特性研究

王亚琦，李琳，崔建业，聂京凯，何强，王帅

（1.新能源电力系统国家重点实验室（华北电力大学），北京 102206；2.国网浙江省电力有限公司金华供电公司，浙江 金华 321000；3.全球能源互联网研究院有限公司，北京 102209）

0 引言

高压直流输电以其可靠性高、成本低、维护费用低、对环境影响小等优点，在满足日益增长的电能需求的大容量输电中得到了迅速发展[1-10]。换流站是高压直流输电工程中直流电与交流电转换的场所，其内部装有众多大容量的滤波电容器，由于有大量的谐波电流流过滤波电容器，且滤波电容器的数量多，尺寸比较大，其可听噪声能够达到105 dB，因此滤波电容器已经成为换流站可听噪声的主要来源之一[11-13]。

目前，国内外已有许多学者针对交流滤波电容器的振动机理及特性进行了研究。文献[14]认为电容器的辐射噪声主要是由于壳体内部的心子元件振动所引起。文献[15-16]建立了双极板电容器模型，分析得出电容器的振动主要来源于极板的振动，且电容器极板间的静电力是电容器振动的激励源。文献[17]对双极板电容器模型进行了受力分析，得出极板所受电场力与激励电压的平方成正比。文献[18]通过试验得出电容器外壳的振动加速度与极板所受的电场力频率相同，均与激励电压的平方成正比。文献[19-20]研究得出了在含有谐波情况下，电容器外壳的振动频率主要包含基波和谐波频率的两倍频、和频和差频分量，总结了谐波初相位等因素对电容器噪声影响的规律，并且通过实验发现，电容器外壳振动在不同表面呈现不同的形式。文献[21-22]提出不同频率的振动激励会对电容器壳体产生不同的响应，并且基于微穿孔板吸声器和可压缩空腔结构，分别提出了滤波电容器的降噪措施，并且通过实验表明，两种方法降噪效果明显。文献[23-25]通过实验测量得出电容器振动主要集中在顶面和底面，且其振动加速度的幅值可以达到4 个侧面的4～6 倍；文献[26]通过建立激光振动测量系统，对换流站中正在运行的电容器装置的振动进行了测量，分析了整个电容器塔架的振动特性，进而研究了电容器装置整体噪声辐射的方向性。

与交流滤波电容器不同，直流滤波电容器在实际运行过程中在承受交流谐波电压作用的同时，也承受直流电压的作用。针对直流滤波电容器的研究，文献[27-28]对直流滤波电容器进行了噪声试验特性研究，指出直流滤波电容器的噪声与交流电容器不同，其频率分为两个部分，谐波频率本身项和谐波差频、和频与倍频项。在实际直流输电工程中，谐波频率项是噪声的主要部分，且直流电压主要影响噪声大小，而交流谐波不仅影响噪声大小，还决定噪声频率。从电容器整体声功率级看，其与所加载直流电压的对数呈正比。电容器壳体内部的心子元件作为电容器辐射噪声的主要来源，他是由两层铝箔片以及铝箔片中间的聚丙烯薄膜卷绕而成的。现有关于滤波电容器的研究均是将其看作双极板电容器模型进行的，而忽略了极板内部的具体结构。心子元件在卷绕过程中，由于静电的作用，聚丙烯薄膜的表面会存在一部分静电荷，此部分静电荷不随时间变化，对于直流滤波电容器来说，由于激励存在直流分量，聚丙烯薄膜作为电介质，其表面会产生极化电荷和弛豫电荷。上述3 种电荷在双极板模型中并没有显示，因此有必要对上述3 种电荷对心子元件振动的物理机理和影响进行分析。

基于上述背景，本文针对直流滤波电容器运行时交直流复合激励的特点，建立了电容器心子的场路耦合模型，综合考虑了电容器心子内部介质薄膜表面的极化电荷、静电电荷和弛豫电荷以及金属极板上的自由电荷，对电容器内部心子的振动特性进行了理论分析、仿真计算及实验验证。

1 交直流复合激励下滤波电容器元件的振动机理

通常的滤波电容器结构主要包括箱壳、双套管、箱底和箱盖以及吊攀组成。箱壳内部为若干个电容器元件通过并联、串联的方式并采用压装、焊接的手段连接在一起组成一个心子，然后进行压装、包封，再通过与铜片焊接作为引出线与套管内部连接线相连接，之后通过抽真空、注油、浸渍的方式注入绝缘油，以提高绝缘性能，最终再通过高压试验形成成品电容器，其结构见图1。

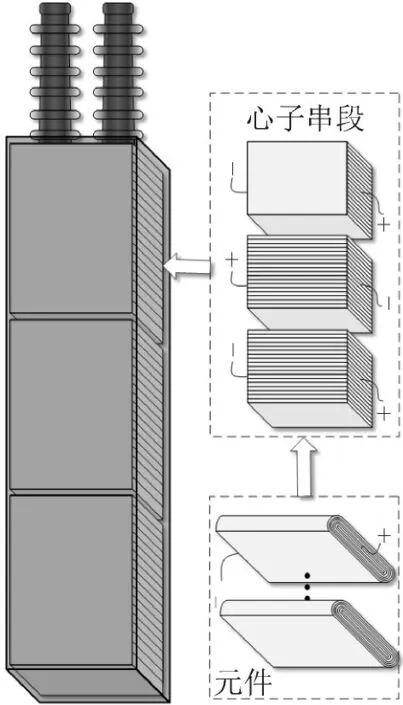
图1 滤波电容器结构Fig.1 Structure of power capacitor

1.1 考虑心子内部电介质表面静电电荷的心子受力分析

电容器心子在生产过程中，聚丙烯薄膜与铝箔通过卷绕机卷绕成圆筒状，随后通过金属板对其进行挤压，形成扁平状结构，最后对其施加直流电压使其内部收缩变紧。在此过程中，由于静电的作用，会导致在心子内部聚丙烯薄膜的表面残余一定数量级的电荷，且此部分静电电荷分布是不均匀和不规则的[29]。这部分电荷不随外部电压变化，且在电场中受力为

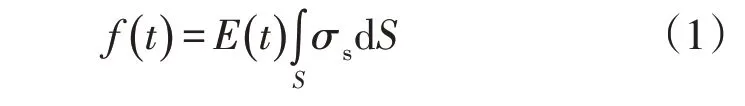
式中，σs为聚丙烯薄膜表面静电电荷密度。与此同时，电场强度与电压间存在关系为

结合式（1）和式（2）可以得出公式为

由此可以看出，由于聚丙烯薄膜表面静电电荷的存在，会使薄膜所受电场力与金属极板上施加的交流电压同频，进而导致产生一部分与交流电压同频的振动分量。

1.2 交直流复合激励时考虑电介质表面弛豫电荷的心子受力分析

图2 为包含两层不同介质的电容器示意图。未接通电源前，两层介质的分界面存在面电荷密度为σ0的静电荷，在t≥0 时，极板两端接通直流电压us，由基尔霍夫电压定律和电荷守恒定律[30]，则公式为

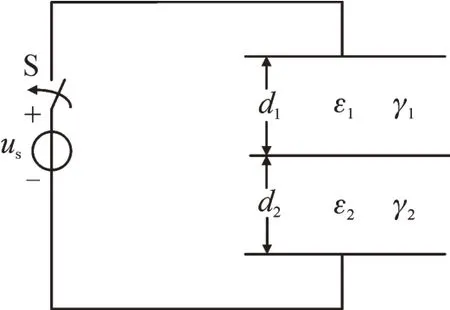
图2 双层介质电容器示意图Fig.2 Schematic diagram of double layer dielectric capacitor

式中，τe为弛豫时间。

为得到E1的初始条件，对式（6）进行积分，有

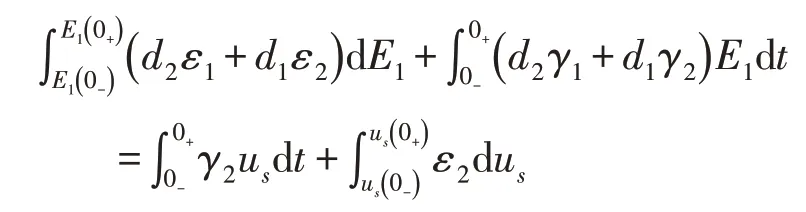
由于接通电源前，介质的分界面上存在面电荷密度为σ0的静电荷，所以E（10-）=（fσ0），us（0-）=0，us（0+）=us，（d2γ1+d1γ2）E1和γ2us为有限值，所以有

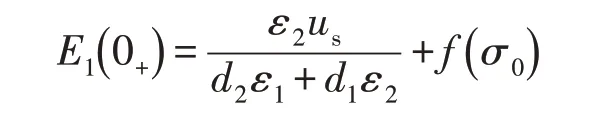
因此接通电源后，E1的过渡过程为

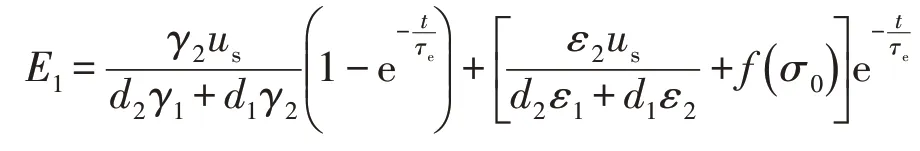
将上式代入式（9）可得

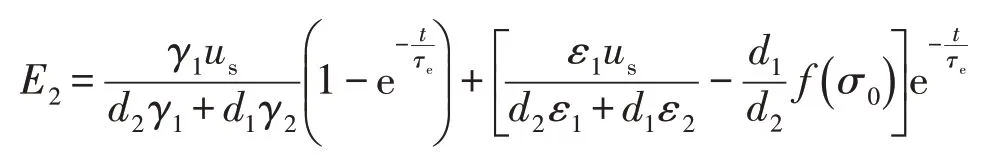
所以分界面上的电荷密度为

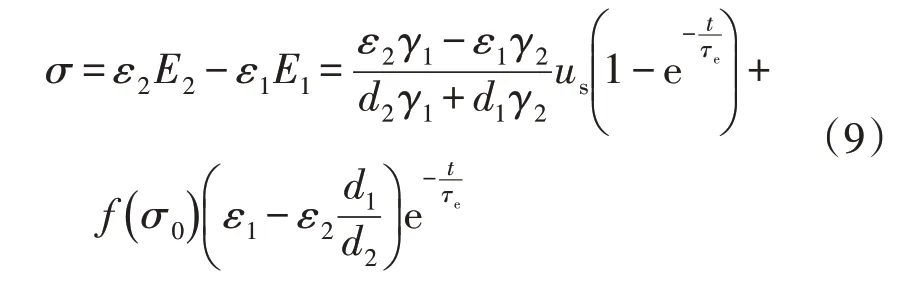
由初始条件可得

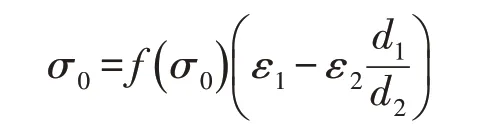
所以分界面电荷密度可以改写为

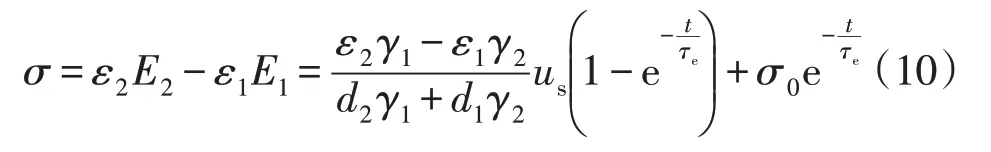
文献[24]中给出了初始时刻分界面不存在静电荷的介质分界面电荷公式为

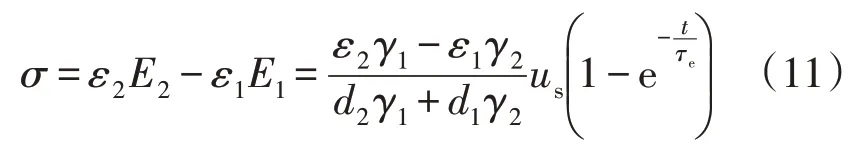
对比式（10）-（11）可得：当不同介质分界面上存在初始静电荷时，影响的是过渡过程中分界面的电荷密度，而达到稳态时，分界面有无初始静电荷对界面电荷结果没有影响。

图3 所示为滤波电容器心子内部的结构示意图，心子内部包括铝箔和聚丙烯薄膜，铝箔和聚丙烯薄膜之间并未完全接触，其间存在一层极薄的绝缘油层。

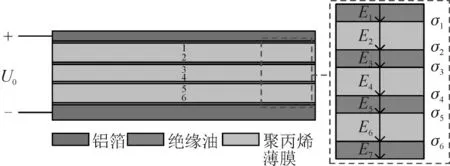
图3 电容器心子内部结构示意图Fig.3 Schematic diagram of internal structure of capacitor core

由于初始时刻聚丙烯薄膜表面存在静电荷σ1-σ6，且每层介质表面初始分布的静电荷各不相同，当电路达到稳态时，为求介质分界面上的电荷密度，由式（10）-（11）可得，初始时刻各分界面不含静电荷时，在达到稳态时的界面电荷即为所求。此时心子的等效电路见图4[31]。其中R1，R2，…，R7为绝缘油层与聚丙烯介质层的电阻，C1，C2，…，C7为绝缘油层与聚丙烯介质层的电容，Rs为电源内阻，us为电源电压。

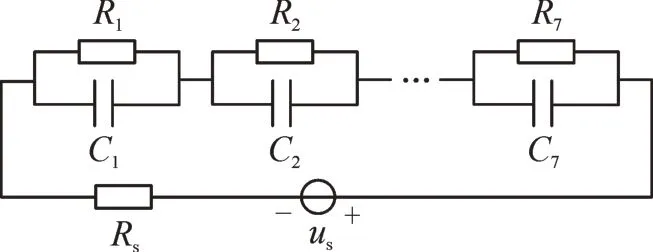
图4 电容器心子等效电路图Fig.4 Equivalent circuit diagram of capacitor core

电容器的等效电路中，电阻参数为

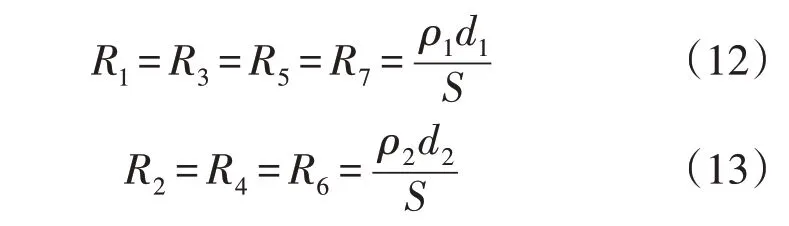
式中：ρ1、ρ2分别为绝缘油和聚丙烯的电阻率；d1和d2分别为绝缘油层和聚丙烯薄膜的厚度；S为心子的面积。

由于R1=R3=R5=R7，R2=R4=R6，所以达到稳态时公式为

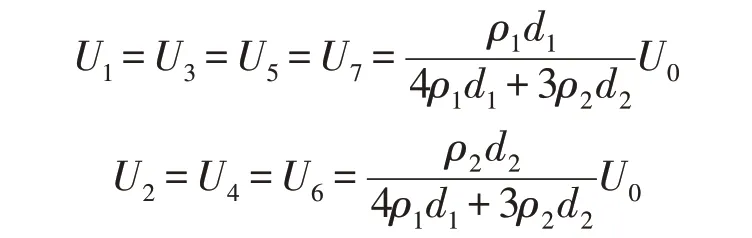
由式（14）可知当电路达到稳态时，公式为

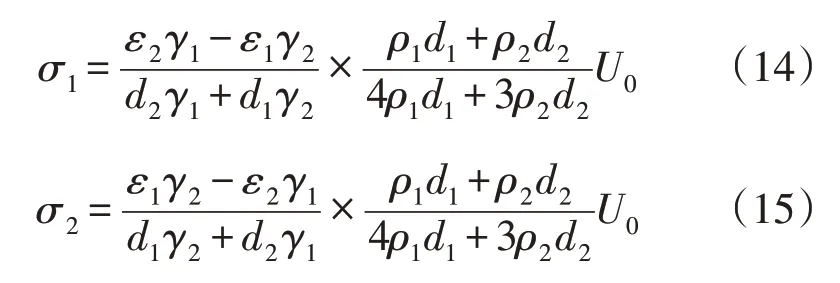
由上可得：σ1=-σ2。同理：σ3=-σ4，σ5=-σ6。

综上所述：在交直流复合激励的情况下，由于直流分量的存在，电路达到稳态时电容器心子内部每层聚丙烯上下表面的电荷极性相反，面密度相等，因此两部分电荷在交流电场中所受的力大小相等，方向相反，导致薄膜受力为0，对心子的振动没有影响。

1.3 交直流复合激励时考虑电介质表面极化电荷的心子受力分析

在交直流复合激励下，由上述等效电路可以求出，电路达到稳态时电容器心子内部各层的电场强度。由于直流激励分量，电容器心子内部聚丙烯薄膜表面会产生大量的极化电荷，且极化电荷的面密度为[30]

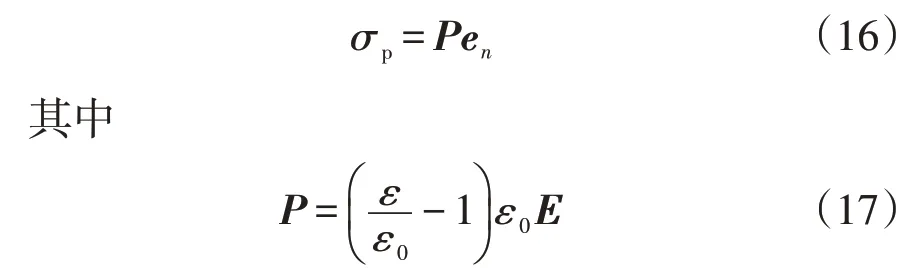
式中，P为电极化强度矢量。

由上述可知，对于电容器心子单元来说，当存在直流时，其内部会产生一匀强电场且聚丙烯薄膜表面会出现极化电荷，极化电荷电荷密度与匀强电场强度成正比，又匀强电场强度与直流电压成线性关系，所以当直流电压越大时，电场强度越大，对应的极化电荷密度越大。但由于极化电荷在产生的过程中是以电偶极子的形式存在，因此将导致薄膜上存在等量的正极性的极化电荷以及负极性的极化电荷，导致薄膜受力为0，因此极化电荷对薄膜振动的影响将不会显现。

1.4 交直流复合激励时电容器心子金属极板受力分析

对于金属极板来说，在交直流复合激励下，由于激励直流分量的存在，极板上会存储两部分电荷：1）激励直流分量引起的稳恒电荷Qd；2）激励交流分量引起的随时间变化的电荷Qa。假设电压激励由直流分量、基波分量、11 次谐波分量和13 次谐波分量组成，则电压激励可以表示为

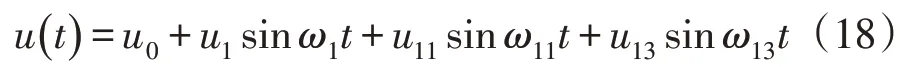
根据Q=CU可知，金属极板上存储的电荷为

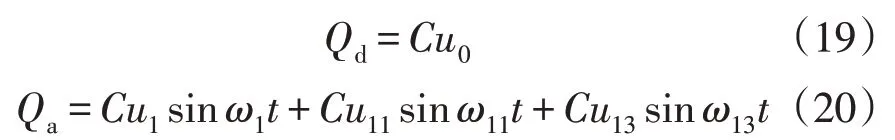
上述两部分电荷在电场中受力为

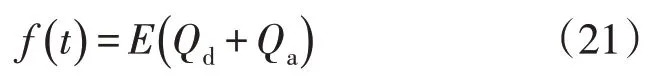
又电容器间电场强度与极板上的电压成正比，E∝u（t），因此电压可以表示为

式中，k为常数。

联立式（18）-（22）可得极板上电荷在电场中的受力为

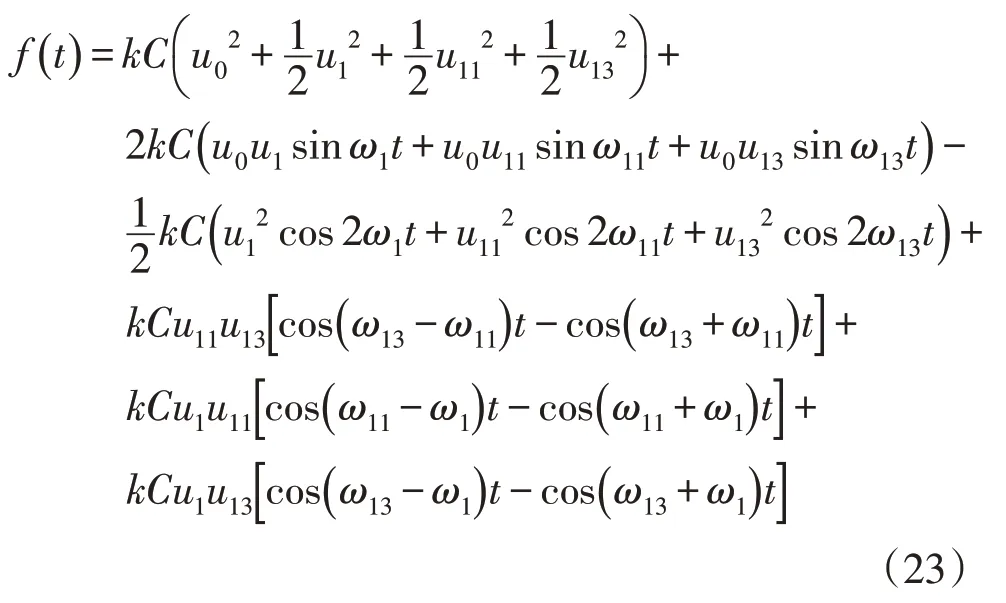
极板的振动主要是由极板上存储的电荷在电场中受力引起的，由式（23）可以看出，极板上电荷受力随时间的变化而变化，且其除去包含激励交流分量基波和谐波频率的两倍频、和频以及差频外，还包含一部分与基波和谐波同频的分量。且激励直流分量主要影响与激励交流分量基波和谐波同频的振动分量，这是导致心子振动的根本原因。

2 仿真计算

使用Comsol 有限元仿真软件对电容器心子中电介质薄膜的受力进行了有限元仿真分析，所选电容器心子由2 层铝箔和6 层聚丙烯薄膜通过卷绕61 圈而制成。但是由于电容器心子内部铝箔和聚丙烯薄膜的层数过多，建立其实际模型比较困难，且很难计算。因此为简化分析并同时对电容器心子内部细节进行考虑，本文取电容器心子最基本的结构作为仿真模型，包括2 层铝箔以及其中间所夹的3 层聚丙烯薄膜。实际电容器心子内部各层薄膜之间以及薄膜与铝箔之间都不是完全接触的，其中会存在一微小的绝缘油层。但是由于本文后续实验所使用心子没有经过抽真空、注油、浸渍处理，因此其内部各层之间存在微小的空气层。在电场计算中，绝缘油和空气的区别表现在相对介电常数的差异[32-35]。为了研究油层和空气层对心子振动影响的区别，分别对心子内部各层之间存在绝缘油层和空气层两种情况进行仿真。具体电容器二维有限元仿真模型见图5。图中A、B、C 为受力采样点。

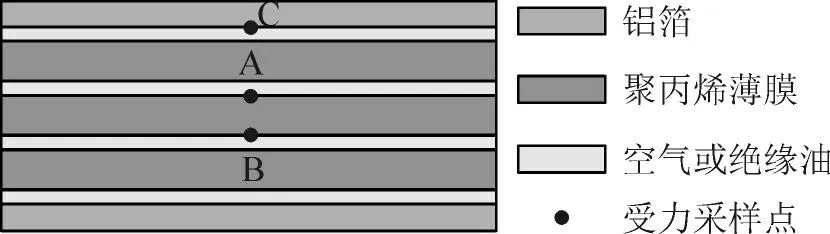
图5 电容器心子二维仿真模型Fig.5 Two dimensional simulation model of capacitor core

在电容器心子金属极板上施加的交流电压分量包含基波、11 次谐波和13 次谐波分量，其中基波电压幅值为71.4 V、11 次谐波分量幅值为42.6 V、13 次谐波分量幅值为14.2 V，直流分量为90 V。采样点A 和B 位于心子内部聚丙烯薄膜的上下表面，采样点C 位于金属极板表面上。

当心子内部各层之间存在绝缘油层且电路达到稳态时，将ε1=2.5，ε2=2.18，d1=1 μm，d2=11.2μm，γ1=0.338×10-13S/m，γ2=0.337×10-15S/m，ρ1=3×1013Ω·m，ρ2=2.97×1015Ω·m，U0=90 V 代入式（13）、式（19）-（20）得：τe=705 s。由于实际电容器模型中极板间有6 个分界面，因此弛豫时间t=4 230 s，σ1=5.09×10-5C/m2，σ2=-5.09×10-5C/m2。

当心子内部各层之间存在空气层且电路达到稳态时，将ε1=1，ε2=2.18，d1=1μm，d2=11.2 μm，γ1=0.33×10-13S/m，γ2=0.337×10-15S/m，ρ1=3×1013Ω·m，ρ2=2.97×1015Ω·m，U0=90 V 代入式（13）、（19）-（20）得τe=317 s。由于实际电容器模型中极板间有6 个分界面，因此弛豫时间t=1 902 s，σ1=5.14×10-5C/m2，σ2=-5.14×10-5C/m2。

由式（10）-（11）可得，聚丙烯薄膜初始时刻是否存在静电荷对薄膜稳态时所含电荷量以及弛豫时间没有影响，因此在仿真研究薄膜稳态状态时，可以考虑薄膜起始时刻不含静电荷对其仿真。图6为采样点A 和采样点B 电荷密度示意图，图7 为电路达到稳态时采样点A 和B 所受电场力示意图，采样点C 所受电场力的频谱图见图8。

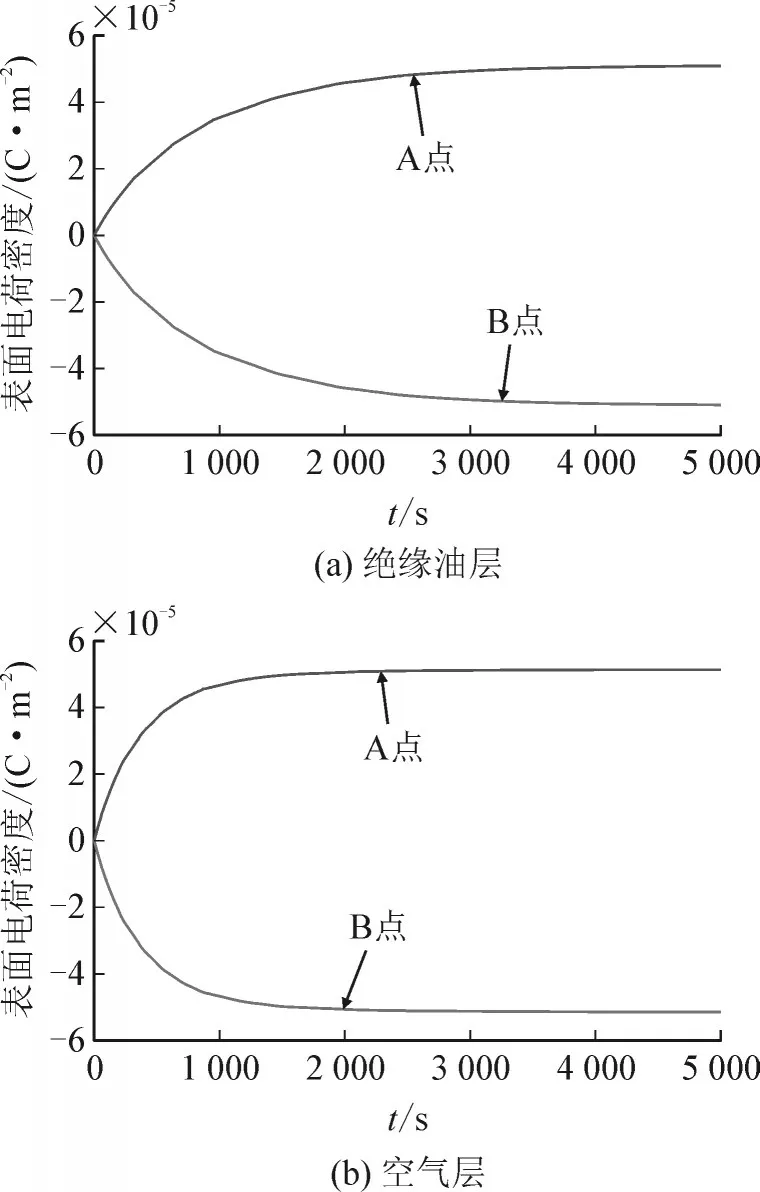
图6 交直流激励下点A、B表面电荷示意图Fig.6 Schematic diagram of surface charge of points A and B under AC and DC excitation

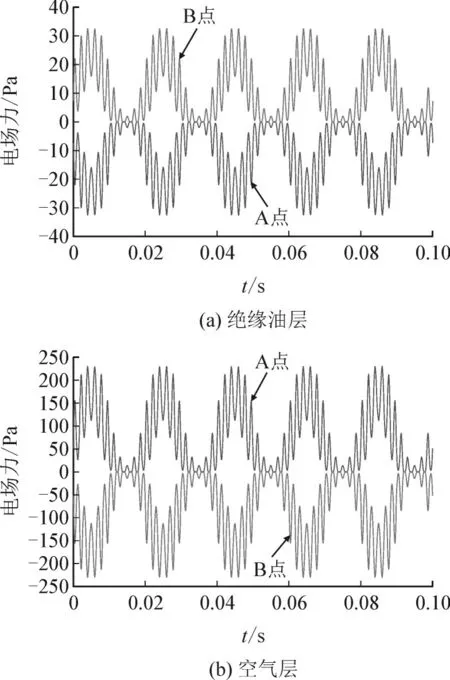
图7 交直流激励下稳态时点A、B所受电场力时域图Fig.7 Time domain diagram of electric field force of point A and B at steady-state under AC and DC excitation

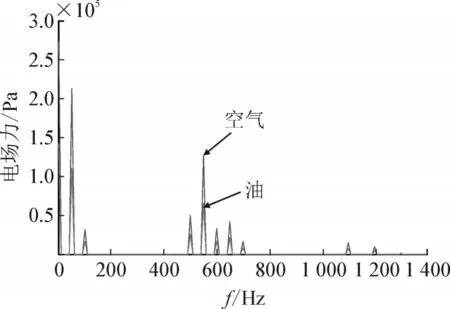
图8 C点所受电场力频谱图Fig.8 Spectrum diagram of electric field force of point C

由图6（a）可以看出，当心子内部各层之间为绝缘油并达到稳态时，聚丙烯薄膜上下表面存在等量的异种电荷，而图6（b）中，虽然心子内部各层之间变成空气，但是达到稳态时，聚丙烯薄膜上下表面仍然存在等量异种电荷，仅仅是弛豫时间以及电荷密度发生了变化，这与理论计算一致。

由图7（a）可知，当心子内部各层之间为绝缘油并达到稳态时，聚丙烯薄膜上下表面所受电场力等大反向。从图7（b）中可以得出，当心子内部各层之间由绝缘油换为空气时，虽然聚丙烯薄膜上下表面的受力方向和大小均发生了改变，但是仍然表现出上下表面受力等大反向的规律，这将导致薄膜最终所受合力为零，不对外表现出振动。

由图8 可以看出，电容器心子内部各层之间存在绝缘油层时，金属极板所受电场力的频谱图中，除去100、500、600、700、1 100、1 200、1 300 Hz 分量外，还存在大量的50、550、650 Hz 分量。当绝缘油层换作空气层时，金属极板所受电场力同样为除去包含100、500、600、700、1 100、1 200、1 300 Hz 分量外，还存在大量的50、550、650 Hz 分量，仅各分量的幅值变大。

3 实验验证

测量电容器心子振动的实验平台见图9。通过对电容器心子单元底部进行竖直固定，通过CSW5550 交直流可编程电源对电容器心子施加激励，采用激光测振仪对电容器心子单元进行振动测试，再将示波器接入激光测振仪采集电容器心子表面振动速度数据。

图9 电容器心子振动测量平台Fig.9 Vibration measuring platform of capacitor core

实验所用的电容器心子单元型号为AAM6.3-470-1W 的电容器心子单元。该电容器由2 层铝箔和6 层聚丙烯薄膜通过卷绕而制成，其尺寸为：长360 mm，宽160 mm，高12 mm，由于激光测振仪的灵敏度非常高，因此实验在一固定桌面上进行，以避免由于实验环境不稳定对振动实验结果造成误差。

实验中电容器心子单元样品见图10，共在表面布置8 个采样点，用激光测振仪测量其振动速度的实时数据。

图10 电容器心子振动测试布点图Fig.10 Vibration measuring points distribution diagram of capacitor core

3.1 电容器心子内部静电电荷对心子振动的影响

在电容器心子振动测试实验中，为研究心子内部聚丙烯薄膜表面生产过程中产生的静电电荷对心子振动的影响，实验所加的激励电压包括基波分量，11次谐波分量和13 次谐波分量，具体加载条件见表1。

表1 交流谐波分量的加载条件Table 1 Loading condition of AC harmonic components

在上述的谐波电压激励下，对电容器心子表面各个采样点的振动进行频谱分析，发现各个采样点具有相同的频率范围，以2 号点为例，其振动频谱图见图11。

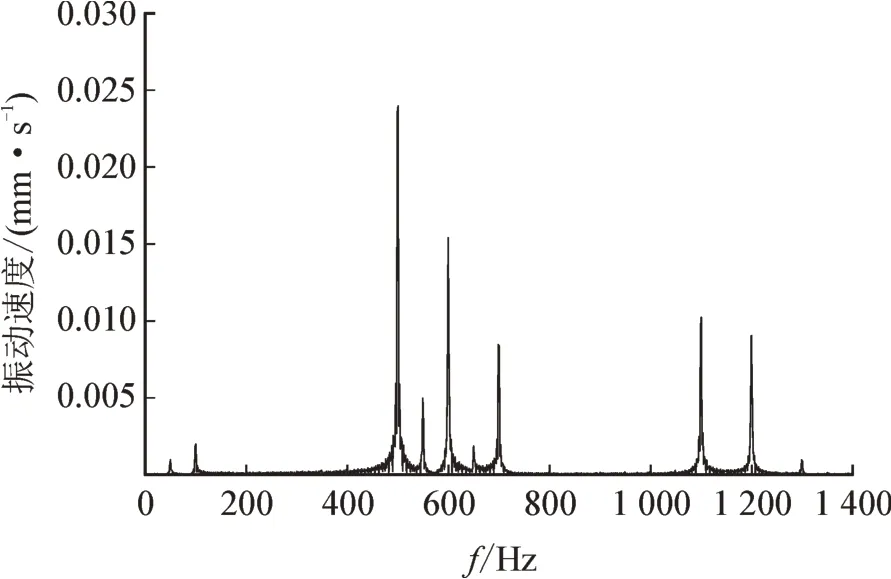
图11 测点2振动频谱图Fig.11 Vibration spectrum diagram of point 2

可以看出，测点2 的振动主要包含除了包含基波和谐波频率的两倍频、和频和差频100、500、600、700、1 100、1 200、1 300 Hz 分量以外，还存在基波和谐波本身频率50、550、650 Hz 分量，且其值与基波和谐波频率的两倍频、和频和差频分量比起来相对较小。这是由于电容器心子生产过程中在其内部聚丙烯薄膜表面产生了静电电荷，导致电容器心子在工作过程中的振动除了包含基波和谐波电压的两倍频、和频和差频的振动以外，还会包含基波和谐波本身频率的振动。但是由于此部分自由电荷量较小，导致基波和谐波本身频率的振动分量较小，实验与理论分析一致。

3.2 直流电压对电容器心子振动的影响

为了研究直流电压对电容器心子振动的影响，试验中保持加载条件交流分量不变，调整直流分量，从30～150 V，以30 V 为步长，具体见表2。

表2 交直流复合激励的加载条件Table 2 Loading conditions of AC and DC compound excitation

对电容器心子表面振动进行频谱分析，发现其具有相同的频谱特性，以在加载组号为3 时点2 的振动为例，其振动的频谱图见图12。

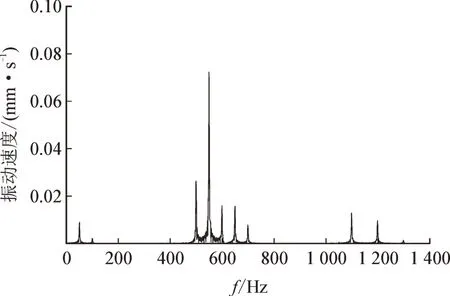
图12 90 V直流+100% 交流谐波激励下点2振动频谱图Fig.12 Spectrum diagram of vibration of point 2 under 90 V DC+100%AC harmonic excitation

可以发现，在交直流复合激励下，电容器心子的振动主要包含50、100、500、550、600、650、700、1 100、1 200、1 300 Hz 分量，且50、550、650 Hz 分量明显比只加交流电压时大。为了研究激励电压的直流分量对振动的影响，取点2 在直流60 V 和直流120 V 2 种激励下的频谱进行对比，见图13。

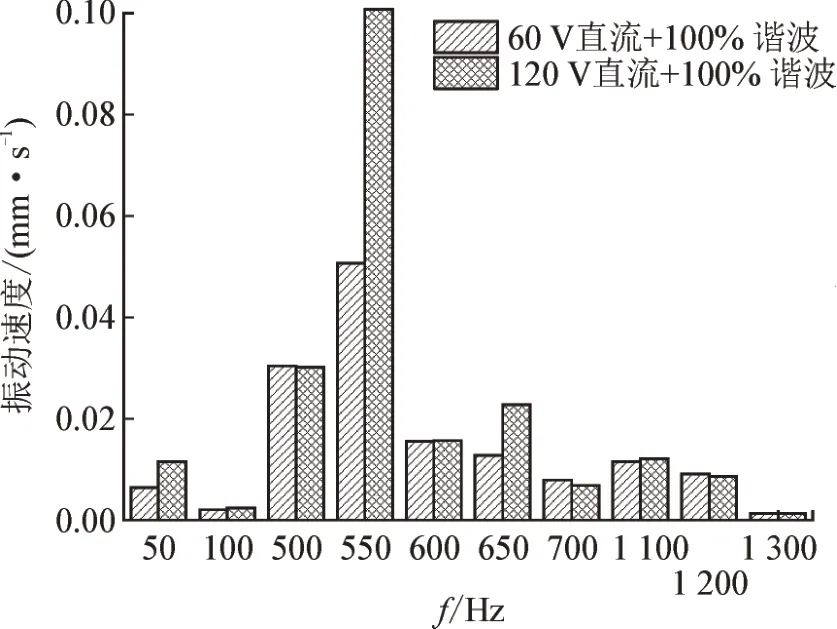
图13 点2在含不同直流激励下振动频谱图Fig.13 Vibration spectrum diagram of point 2 under different DC excitation

可以发现，激励的直流分量主要影响频率为50、550、650 Hz 的振动分量，即激励交流分量基波和谐波本身频率的振动分量，而对基波和谐波频率的两倍频、和频和差频的分量影响很小。且由于激励的交流分量始终为100% 谐波加载，导致基波和谐波频率的两倍频、和频和差频振动速度分量没有明显变化。这与理论分析相一致。

3.3 直流与电容器心子振动的关系

为了研究激励直流分量与激励交流分量基波和谐波本身频率振动之间的关系，取电容器心子表面各测点振动速度的50 Hz 分量，并作出其随直流电压变化的关系，见图14。

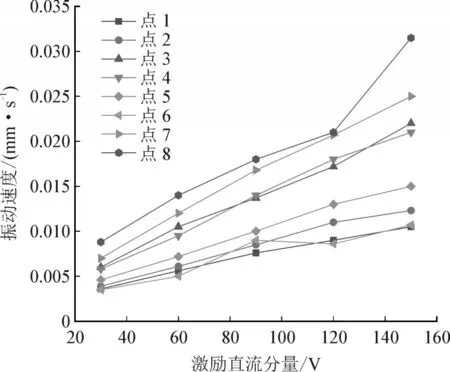
图14 心子表面测点振动速度50 Hz分量随激励电压直流分量的变化图Fig.14 Variation diagram of 50 Hz component of vibration speed of measuring point on the surface of the core with DC component of excitation voltage

可以看出，心子表面振动速度50 Hz 分量与激励直流分量在误差允许的范围内呈线性关系。这是因为直流电压对于电容器心子表面振动有着重要的影响，由式（23）可以看出，激励直流分量主要影响与交流分量基波和谐波本身频率同频的振动速度分量，随着直流电压的增大，与激励交流分量基波和谐波同频的振动分量线性增加。又由于生产过程中产生的残余电荷实际含量较小，因此在激励含有直流分量时，电容器心子表面振动所包含的与激励交流分量基波和谐波本身同频的振动分量将随着直流电压的增大呈线性增大。

4 结语

本文从直流电容器心子的振动机理出发，针对直流滤波电容器交直流复合激励的特点，建立了电容器心子的场路耦合模型。在综合考虑心子内部介质薄膜表面的极化电荷、静电电荷和弛豫电荷以及电容器金属极板上的自由电荷的基础上，研究了心子的振动特性。通过仿真计算以及实验验证了理论的准确性，得到的主要结论如下：

1）电容器心子在生产过程中由于静电原因会在其表面产生少量的静电电荷，此部分电荷在电场中会产生一个与激励同频的电场力，致使心子在交流激励时产生少量与激励同频的振动。

2）直流电容器在交直流复合激励下稳定工作时，心子内部聚丙烯薄膜上会产生极化电荷和弛豫电荷，其中极化电荷由于以电偶极子的形式存在，因此对外显电中性，将不产生交变的电场力，不对外产生振动。驰豫电荷与静电荷分布在电介质薄膜上下表面，且薄膜上下表面带有的电荷量相同，极性相反，导致聚丙烯薄膜受力为零，对外不显示振动。

3）金属极板在交直流激励下会存储一定量的稳恒电荷和随时间变化的电荷，这两部分电荷在电场中受力，使金属极板产生振动。对外表现为心子的振动，致使心子的振动除去包含与激励交流分量基波和谐波频率的两倍频、和频和差频分量以外，还包含有与激励交流分量同频的振动分量。

4）激励的直流分量只影响电容器心子振动中与激励交流分量同频的部分，对激励交流分量基波和谐波频率的两倍频、和频和差频分量没有影响，且与激励交流分量同频的振动分量大小与激励的直流分量呈线性关系。