基于改进包围盒法的碎石土细观结构模型构建及应用

党润萌 雷进生 吴建兵 刘婉纯 石智强 袁宇坤

(1.防灾减灾湖北省重点实验室(三峡大学),湖北 宜昌 443002;2.三峡大学 土木与建筑学院,湖北 宜昌 443002;3.浙江华东工程咨询有限公司,杭州 311122)

注浆技术可用来加固松散碎石土层,以提高其防渗与承载能力[1].张志沛、袁敬强等[2-3]研究了注浆方式和注浆压力对浆液在软土地基中扩散的影响,土体中不含块石,注浆扩散符合马格理论.王东亮等[4]建立了流固耦合下的单一裂隙注浆模型,结果表明裂隙开度和注浆压力对浆液扩散半径影响较大.王立彬等[5]考虑浆液的时变特性研究了浆液的球形和柱面扩散.雷进生等[6]基于非均质地层模型开展注浆数值模拟计算,指导和评价了桩周注浆加固过程.这些研究是以均质土层或非均质土质为注浆介质,在此基础上,研究以碎石土为注浆介质的地层加固效果,为碎石土土层注浆加固技术提供理论依据.

碎石土是由残坡积、风化卸荷及冲洪积等形成的第四纪土与石块的二重介质非均质土石混合体,是一种特殊的地质体[7].目前,在碎石土的物理力学性质[8-10]、碎石土边坡稳定性及防治措施等[11-12]方面开展了较深入的研究,并取得了大量成果.在利用模拟技术生成碎石土细观结构模型方面,宋来忠和张宏明等[13-14]通过随机模拟方法建立土石混合体的随机结构模型,模拟了土石混合体中块石的几何形态、空间分布.针对块石随机投放中边界不相交的判断准则主要基于几何体中心间距大于最大半径之和.

本文为探究碎石土地层的注浆扩散特性,构建碎石土细观结构模型,利用蒙特卡罗法构建土石颗粒库,在矩形包围盒法对生成的块石进行初步判断的基础上,针对块石相交或包含的特殊情况改进其算法,快速排除空间位置不合理的块石,构建更为随机分布的几何模型.基于Weibull分布函数赋值土、石参数构建二维碎石土注浆扩散模型,研究在不同含石率下注浆压力和初始地层参数对浆液扩散的影响,同时为碎石土层的注浆加固工程提供理论依据.

1 块石形态的随机生成方法

蒙特卡罗法是一种由统计抽样理论所确定的随机变量在计算机上模拟的数值计算方法.蒙特卡罗法与有限元等数值方法相结合而发展起来的随机有限元法、随机边界元法等方法逐步发展,相比于其他方法,生成的块石更加自然化.

利用蒙特卡罗法来生成土石混合体中块石的随机形状,可以建立一批随机生成的土石颗粒库.单个多边形块石的生成方法是在预先生成的随机圆的基础上,按逆时针方向随机生成若干顶点,再依次连接各顶点就能生成随机的多边形.自然生成的块石颗粒一般为形状各异的不规则多边形,一般取碎石颗粒多边形的边数n为3～8.

1)在极坐标中,多边形的形状可由边数n、极角θi和极半径ri来定义.通常碎石颗粒形状各异,仅含某一种较规则的几何图形是很少见的,抽象出的不规则多边形边数也在某一范围内变动.生成碎石的多边形具体边数n由随机数控制,通过以下方法给定正整数n.

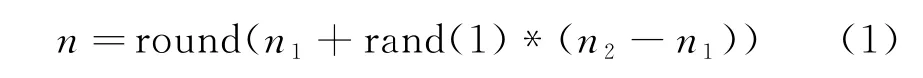
式中,round()为取整函数;rand()为随机数生成函数,rand(1)表示生成的随机数在0～1间;n1,n2是块石颗粒的最小和最大边数,分别为3,8.生成一组随机的角度增量{θ1,θ2,θ3,…,θn},其中,

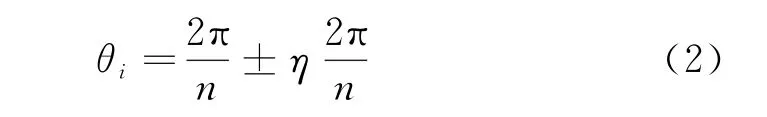
式中:η为角度增量系数,取值越小,角度增量更小,几何形状越规则.

在角度增量过程中还要满足式(3)所示的两个条件.

2)以预先生成的角度增量从圆心向外引出射线,与圆的交点即为多边形的端点{θ1,θ2,θ3,…,θn},这时圆心到端点的距离均为半径r,在此基础上生成一组新的长度增量{L1,L2,L3,…,Ln}.

式中:ξ为长度增量系数(-1≤ξ≤1),人为地定义极半径的变化幅度.

根据上述过程得到的{θ1,θ2,θ3,…,θn}和{L1,L2,L3,…,Ln}可以生成随机形状的块石,基于Monte-Carlo方法的随机采样法过程如图1所示.

图1 块石颗粒转化示意图

2 块石的空间随机分布方法

2.1 AABB矩形包围盒相交判断法

解决模拟细观结构中块石空间随机分布的问题,可采用包围盒法.包围盒法是一种求解离散点集最优包围空间的算法,基本思想是用体积稍大且特性简单的几何体(称为包围盒)来近似地代替复杂的几何对象.常用的包围盒有AABB(Axis Aligned Bounding Box)包围盒[15]、OBB(Oriented Boun-ding Box)包围盒[16]和球包围盒[17].AABB 矩形包围盒是能够包围原物体的最小轴向包围盒;OBB 包围盒则在 AABB包围盒的基础上考虑了物体的朝向;球包围盒则是能够包围原物体的最小圆形.球包围盒是最简单的检测方法,虽然精度较低,但效率较高;OBB 具有较高的精度,但是效率低;相比于其他包围盒法AABB 包围盒在精度和效率方面都是最优的.

SHEN 等[18]提出了AABB矩形包围盒相交判断法.AABB矩形包围盒相交判断法是基于点、线段和矩形矢量关系的判断相交的检验算法.

首先构造3个矩形盒,其中公共矩形盒的边长为[xmax-xmin,ymax-ymin];两个个体矩形盒边长分别为[x1max-x1min,y1max-y1min],[x2max-x2min,y2maxy2min].然后通过以下条件对两个个体矩形盒的相互关系进行判断:

①矩形盒相离

②矩形盒接触

2.2 土石颗粒生成与投放

用矩形包围盒间相交关系来判断石块是否相互干涉,将投放目标区域划分为一定面积的矩形网格域,在此区域进行块石随机投放.确定与该块石矩形包围盒交叉的所有网格域,找到所有相交网络后,进行全局相交判定,如图2所示.

图2 矩形盒包围示意图

在块石投放时,关键的一点是“新块石”与“老块石”之间的干涉判断,块石间的相对关系主要有相离、接触、相交、包含4种.对于生成的二维土石混合体模型,相交和包含均须剔除.具体判断如下:

1)块石与边界干涉判断.

块石与边界的干涉判断只需要满足个体矩形盒属于投放范围即可.

2)块石之间的干涉判断.

矩形盒间的关系并不能代表块石间的相互关系,其中矩形盒相离对应块石的关系为相离;矩形盒接触时若新老块石中有一个点的坐标重合,则块石关系为接触,否则相离;如图3所示,矩形盒相交时还需要对其中几个特殊的情况按顺序进行下一步的判断:①若一块石存在某一点位于另一块石中,则两块石相交;②若不相交但某一块石存在一点在另一块石边上,则两块石接触;③其余情况两块石相离.

图3 矩形盒相交时的关系判断

如图4所示,矩形盒包含时也需要对其中几个特殊的情况进一步地判断:①若新块石或老块石所有点在另一块石中、边上且另一块石无点在原块石中,则两块石包含;②若不属于①的情况,但一块石存在某一点存在另一块石中,则两块石相交;③若不属于以上情况,但一块石存在某一点在另一块石边,则两块石接触;④其余情况两块石相离.

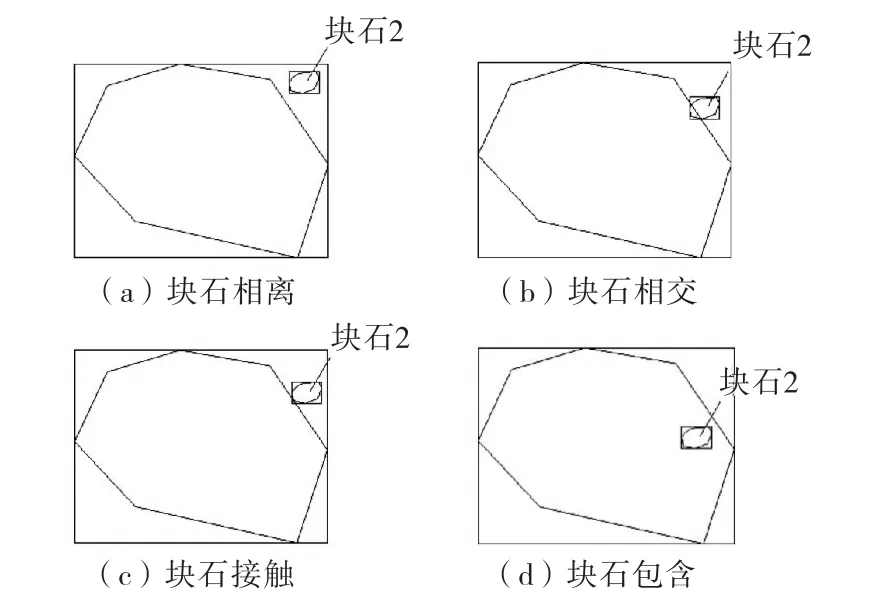
图4 矩形盒包含时的关系判断

2.3 改进的边界干涉算法

遇到矩形盒相交或包含的特殊情况时,需要进行块石位置关系的精准判断,通常的做法是遍历多边形所有边来进行相交判断[19],若相交、包含矩形盒中的2个块石所有线段均不相交,则两块石相离或接触;若存在线段相交情况,两块石相交.当研究区域内的块石数量过多时,后期投放需要遍历所有已生成块石各边,应用该算法时计算效率较慢,不利于多次高精度的数值模拟.

为了提高运算时的速度,通过判断块石端点是否包含于另一块石中来判断块石的相交情况,若存在一端点在已有块石内,则判定两块石相交或包含;否则两块石相对位置满足投放要求.

首先提取生成多边形的各角点,并按顺时针排序的方式生成该多边形.假设待判断点为点Q,从点Q水平向左或向右引一条无限长度的水平射线,在射线延伸过程中与多边形相交得到了一系列点[L1,L2,L3,…,Ln];若系列点的个数为偶数,则代表点在多边形外部;若数量为奇数,则代表点在多边形内部;若遇见射线与多边形有无穷个交点,则判断射线是否与多边形重合,点在多边形外部.如图5所示.

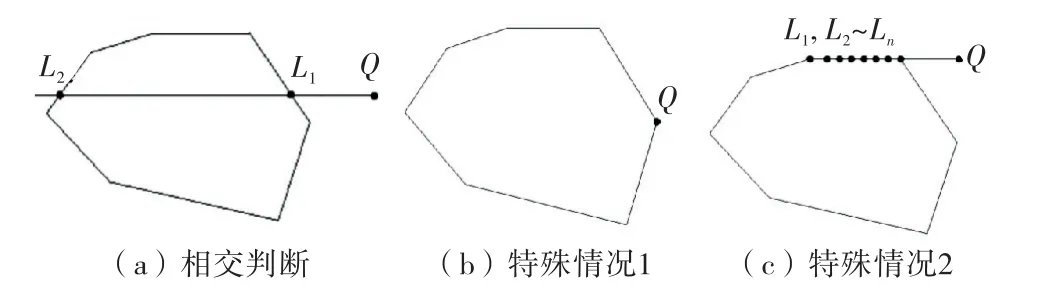
图5 点与多边形的位置判断

同时需要注意以下几种特殊情况:

1)点Q在多边形端点上,可直接判断为内部;

2)点Q恰好在多边形某一水平边或其延长线上.

在块石颗粒进行随机投放时,如果不对粒径加以控制,在几次投放后小型块石占据了区域各个位置,则会出现大块石投放困难、小块石偏多的情况,于是在算法中需要考虑控制粒径的大小,分析同样含石率下不同级配分布的块石形态.采用的方法是,在投放时按照大→小的顺序进行投放.让判断困难、占地面积大的部分优先投放,达到相应的级配后则开始下一范围的颗粒继续投放.不同含石率的块石几何模型如图6所示.

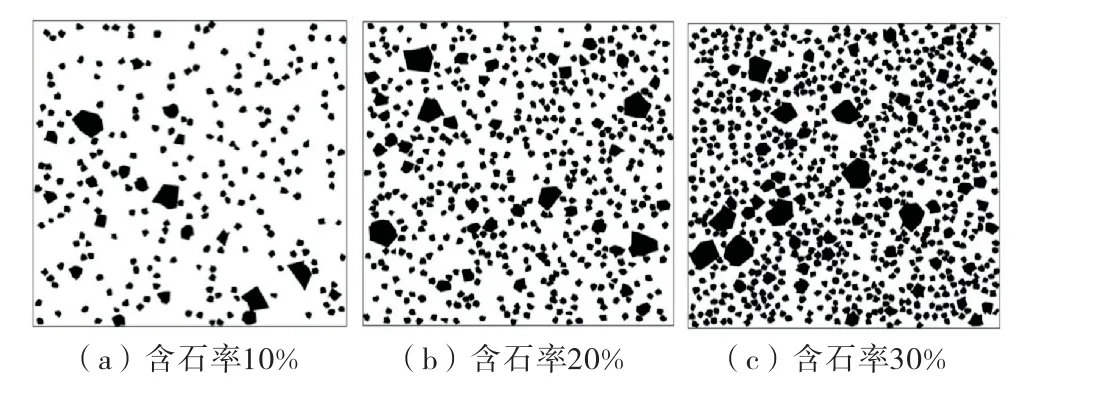
图6 碎石土地层几何模型

3 细观模型在实际中的应用

基于蒙特卡罗法构建碎石土中块石形态,基于改进包围盒法生成块石的空间随机分布,利用Weibull分布函数和改进算法结合,描述土、石参数分布规律,可构建出碎石土力学模型[20].以初始孔隙率为基础利用概率方法建立考虑土体参数相关关系的随机地层模型[21],结合流固耦合理论,构建二维注浆加固模型[22].

3.1 注浆扩散模型计算

1)模型建立:采用平面单孔注浆模型,地层纵向剖面范围为4m×10m,注浆孔直径为0.08m,深度为8m.注浆计算采用三角形网格,单元数88757个,自由度355772个.

2)边界条件:对于应力场,底部为固定约束,两侧为滚轴约束.对于渗流场,注浆孔的注浆范围为-8～-1m.

3)计算参数:以某地质灾害治理现场碎石土为例,含石率为7%～15%[23],取土/石阈值为15mm,将小于这一粒径的块石视为等效土体颗粒.对土体和块石的物性参数分别取值.注浆过程涉及土体参数、块石参数、注浆工艺及浆液参数3个方面.模型参数见表1～3.

表1 土体参数表达式

表2 块石参数表达式

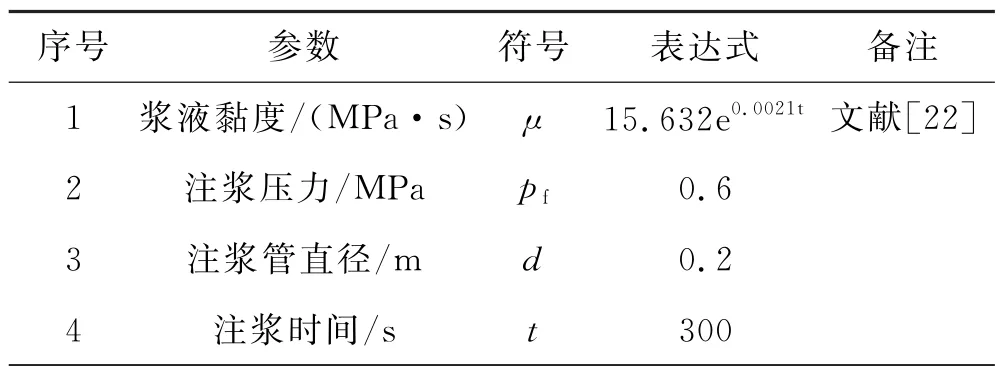
表3 注浆工艺及浆液参数表达式

研究碎石土地基的注浆加固行为,注浆压力、注浆时间以及地层的物性特征都是影响浆液扩散的关键因素.含石率7%的地层初始孔隙率分布和网格划分如图7～8所示.

图7 孔隙率随机分布

图8 有限元网格划分

3.2 浆液扩散形态分析

理论上的流体扩散边界应为pf=0的位置,但浆液不是理想流体,渗透需要一定的启动压力[22].注浆扩散范围采用渗透压力指标评定,以大气压力为基准,注浆压力为0.6MPa,不同时刻浆液的扩散范围如图9所示.考虑浆液黏性时变时的扩散半径为[21]

式中:A为黏性时变系数;k为砂粒渗透系数(cm/s);β为浆液与水的黏度比;r0为注浆管半径(cm);r1为浆液的扩散半径(cm);h1为注浆压力头(cm);t为注浆时间(s);μg0为浆液的初始黏度(Pa·s).

由图9可知,与经典柱形注浆锋面不同,浆液扩散锋面呈不规则分布,与杨溢等[1]对砂砾石层的现场注浆试验中注浆扩散形态及预测模型一致.前期随着注浆时间的变化,扩散半径增大非常明显,在100s左右浆液扩散趋于稳定,浆液扩散呈现出“绕石性”,块石在作为非多孔介质时对浆液的扩散有阻碍作用.

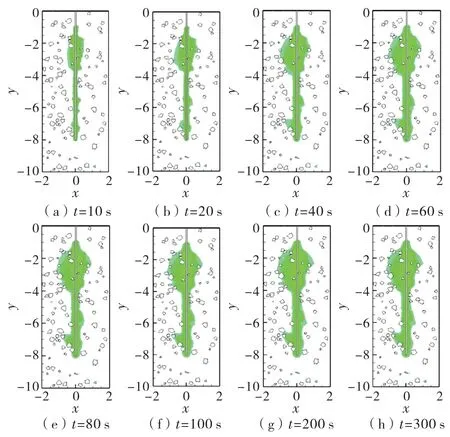
图9 浆液随注浆时间扩散形态

浆液在碎石土中的渗透扩散实质上是浆液在注浆压力的作用下克服土体阻力做功、占据土体孔隙、排出“水”、“气”的过程,在渗透系数更大的位置浆液扩散明显更加容易,随着浆液压力的衰减及浆液黏度变化,浆液运动速度逐渐下降,注浆过程逐渐趋于稳定.由于石的渗透率很小,浆液在土体中几乎是沿着石头表面绕行进行渗透,可以看出块石对浆液的渗流扩散有一定的阻碍作用.

3.3 注浆压力对浆液扩散的影响

由于块石在地层空间分布中的随机性,需要进行大量的数值模拟试验来统计得到较为准确的变化趋势,浆液最大扩散半径随压力的变化情况如图10所示.在不含块石的情况下,注浆压力为0.7MPa时,浆液已经扩散到了模型边界.注浆压力越大,克服孔隙压力以及浆液黏滞阻力的能力越强,浆液扩散范围越远.从总体趋势来看,最大扩散半径随着注浆压力逐渐增大,变化趋势与块石含量无关.

图10 最大扩散半径随注浆压力变化

3.4 含石率对扩散范围影响

在不同注浆压力下,最大扩散半径均随着含石率的增加而减小,说明块石颗粒对浆液在土体中的渗流扩散有明显的阻碍作用.不同注浆压力pf、不同含石率R下的最大扩散半径情况如图11所示.

图11 最大扩散半径与含石率关系

4 结论

1)提出一种改进的碎石土体数值模型构建方法.利用Monte-Carlo模拟法构建考虑棱角性的块石模型库,结合改进包围盒法进行块石随机空间分布,将Weibull分布函数和改进算法结合,描述土、石参数分布规律,实现碎石土细观模型的构建.

2)AABB矩形包围盒相交判断法是基于点、线段和矩形矢量关系的判断相交的检验算法.在利用AABB矩形包围盒判断块石位置的基础上,遇到矩形盒相交或包含的特殊情况时,需要进行块石位置关系的精准判断,通过判断块石端点是否包含于另一块石中来判断块石的相交情况,若存在一端点在已有块石内,则判定两块石相交或包含,在此基础上改进算法,加快块石干涉算法,加快生成土石混合体几何模型.

3)基于改进的AABB 矩形包围盒法构建土石混合体几何模型,可充分考虑块石的位置和分布,进行碎石土介质注浆扩散范围模拟,分析浆液在孔隙率等地层物性特征空间随机分布下的扩散过程.模拟结果表明,注浆前期随着注浆时间的变化,扩散半径增大非常明显,在100s左右浆液扩散趋于稳定,浆液扩散呈现出“绕石性”,块石在作为非多孔介质时对浆液的扩散有阻碍作用.在渗透系数更大的位置浆液扩散明显更加容易,随着浆液压力的衰减及浆液黏度变化,浆液运动速度逐渐下降,注浆过程逐渐趋于稳定.最大扩散半径随着注浆压力逐渐增大,变化趋势与块石含量无关.根据施工现场土层含石率调整注浆参数,为碎石土层注浆加固工程提供理论依据.