基于模糊逻辑的三电平T型逆变器故障诊断研究
李 文 帕孜来·马合木提 李高原
(新疆大学 电气工程学院,乌鲁木齐 830017)
随着逆变器技术的发展,产生了许多新型逆变器.其中,三电平T 型逆变器凭借交流输出谐波小、开关损耗低和效率高等诸多优势被广泛应用,现已得到国内外学者的高度关注[1].逆变器功率管的故障类型有开路故障和短路故障.短路故障发生时间较短,通常为几微秒,不易检测,系统中通常会串联快速熔断器等硬件保护电路,可将短路故障转化为开路故障进行处理[2].本文研究三电平T 型逆变器的开路故障,所提及的故障均为IGBT 的开路故障.常见的逆变器开路故障诊断方法有基于解析模型、知识和数据驱动的方法[3-4].文献[5]使用Park矢量法对三相两电平逆变器进行故障识别,这种方法需要识别归一化电流平均值的正负属性,根据故障定位变量是否超过阈值从而确定故障标志,由故障标志确定故障管.但是,该方法在确定阈值的时候需要通过大量实验得出.文献[6]使用逆变器输出功率对IGBT 进行开路故障诊断,由于依靠功率作为故障特征,故用该方法在设备空载的情况下进行诊断很容易出现误诊断.文献[7]对三电平逆变器进行逻辑建模,对实际模型和故障模型进行特征提取,通过对比实际模型与故障模型的残差从而识别出故障类型.但是,该方法需要复杂的逻辑建模,而且模型与实际系统往往存在一定的误差.文献[8]将逆变器输出三相电压信号转化为两相信号作为特征量,利用神经网络对其进行辨识从而识别故障管,但是该方法需要大量的训练数据,诊断速度慢.
本文使用模糊逻辑对三电平T 型逆变器进行故障诊断,对逆变器的输出电流求均方根值和平均值,以均方根电流值和电流平均值作为特征量,使用模糊逻辑对该特征量进行辨识.实验表明,通过建立的模糊规则,可以准确识别出故障类型.该方法不需要复杂的数据计算,诊断时间短,能准确识别出故障类型.
1 模糊逻辑
模糊逻辑在模糊控制和系统辨识领域发挥着重要作用.在处理辨识问题时通常分为以下步骤:模糊化,模糊推理,去模糊化.对于经典的布尔逻辑,只能辨识“0”或者“1”,其基本运算是“与”、“或”、“非”.但对于模仿人脑的计算方式,布尔逻辑已不能满足需要,模糊逻辑便用来解决一些模糊分类和决策问题.
1.1 模糊化
模糊化是模糊逻辑的前提,是将模糊器输入的精确量转化为模糊量.模糊集合基于数学的思维方法,定量处理事务和概念的不确定性或模糊性[9].模糊化的过程主要是建立故障征兆集X和故障原因集Y;再构造模糊隶属度函数,建立模糊矩阵R;最后通过模糊算子合成算法,求解模糊方程,确定故障原因[10].式(1)为故障征兆向量.式(2)为故障原因向量,表示故障征兆出现的原因.对于集合A,x属于X,μA(x)为隶属度,其值介于0和1之间,如式(3)所示.μA(x)的值越大,表示事件x发生的可能性越大.

1.2 模糊规则
建立模糊规则旨在建立模糊关系矩阵,模糊关系矩阵是根据故障征兆和故障原因之间的模糊关系建立的,如式(4)所示.R为模糊关系矩阵,该矩阵中的元素值介于0和1之间,表征故障征兆X与故障原因Y关联性的量化值[11].矩阵中的元素值越大,表示从故障征兆推理出故障原因的可能性越大.模糊推理如式(5)所示,其中Y表示故障原因向量,“·”表示模糊算子.

1.3 去模糊化
当数据模糊化完毕之后,需要去模糊化以便形成精确量.常用的去模糊化方法有最大隶属度法、重心法和加权平均法[12].其中重心法去模糊化由于其计算方便,适合用于分类问题.本文使用的是重心法去模糊化,如式(6)所示.
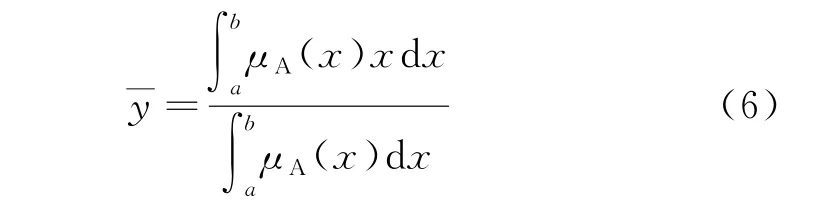
式中:μA(x)为隶属度.
2 特征提取
2.1 三电平T型逆变器拓扑
图1为三电平T 型逆变器拓扑结构.该拓扑结构中IGBT 发生开路故障概率大,相应的故障诊断研究尤为重要[13].开关管的短路故障一般需要在微秒级的时间内检测到并给予排除,目前主要采用成熟的硬件检测和保护方案[14],在此不进行诊断.本文主要研究三电平T 型逆变器IGBT 开路故障,其中包括单管开路故障和双管开路故障.由于三电平T 型逆变器三相对称的缘故,本文的故障分析选取其中两相.

图1 三电平T 型逆变器拓扑结构
2.2 故障特征提取
首先需要测量每相均方根电流值,判断每相均方根电流值是否相等.如果相等,则无故障发生,如式(7)所示.正常无故障情况下,每相均方根值相等.如果均方根值不相等,则判断有故障发生,此时需要测量电流平均值,如式(8)所示.式中,N表示一个周期内的电流采样次数,i(n)表示三相电流值.

2.3 诊断策略
判断有故障发生后,需要进一步判别是哪一种故障类型.此时运用模糊逻辑,将三相电流平均值模糊化,运用模糊规则,反模糊化后可以准确识别故障管.诊断策略的示意图如图2所示.

图2 诊断策略
其中,故障征兆向量为逆变器输出的三相电流平均值的相对大小,每一相有13种故障征兆向量,分别为NVB(负极大),NB(负大),NM(负中),NS(负小),NVS(负极小),NVVS(负最小),ZO(零),PVVS(正最小),PVS(正极小),PS(正小),PM(正中),PB(正大),PVB(正极大).其中NVB 表示电流平均值模糊化后达到负极大值的范围,NB 表示电流平均值模糊化后达到负大值的范围,以此类推.由于Sa1和Sa3管故障时,B 和C 两相的电流平均值太小,介于0~0.2A,如图3所示.所以设置了NVVS和PVVS这两种故障征兆向量对其进行辨识.

图3 Sa1 和Sa3 管0.06s开路故障平均电流
由于T 型逆变器三相对称缘故,所以诊断选择的单管故障为A 相的4个功率管Sa1、Sa2、Sa3、Sa4.双管同相故障选择A 相的两管故障.双管异相故障选择A、B 两相的不同相两管故障,总计20种故障.其中Ia为A 相电流的平均值,Ib为B 相电流的平均值,Ic为C 相电流的平均值.当Ia的故障征兆为NB,Ib为PVS,Ic为PVS时,应用模糊规则后即可识别为Sa1故障.同理,当Ia模糊化后为NVB,Ib为PS,Ic为PS时,应用模糊规则后即可识别为Sa1和Sa2故障,模糊规则见表1.
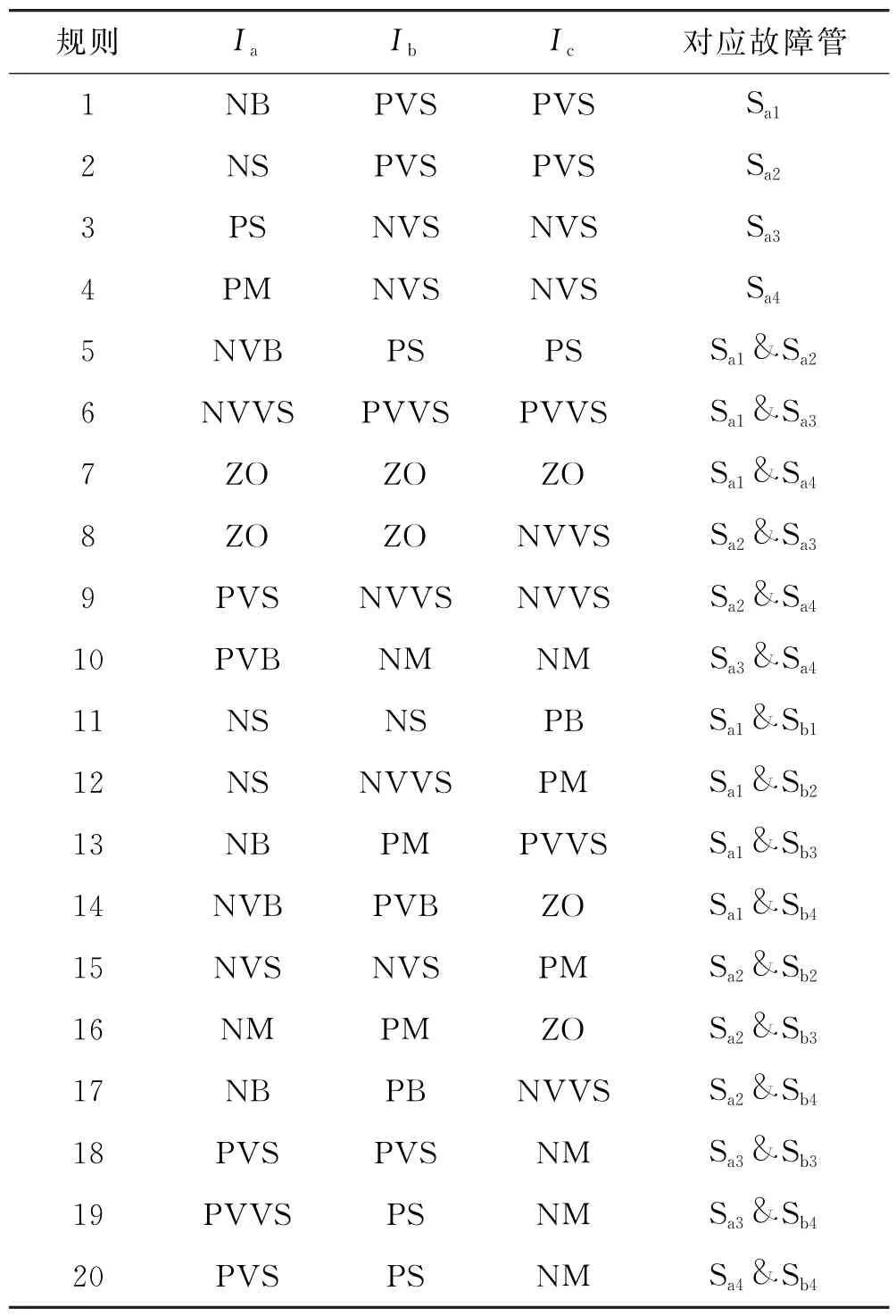
表1 模糊规则表
3 实验结果
本文仿真实验模型在Matlab/Simulink 环境中搭建.如图4所示.整个模型由脉冲电路、滤波电路、测量电路和模糊分类构成.其中LCL滤波电路如图5所示,主要由滤波电感和滤波电容构成.由于三相对称,因此A,B,C三相的滤波电感和电容参数相同.仿真参数见表2.

图4 仿真模型

图5 LCL滤波电路结构
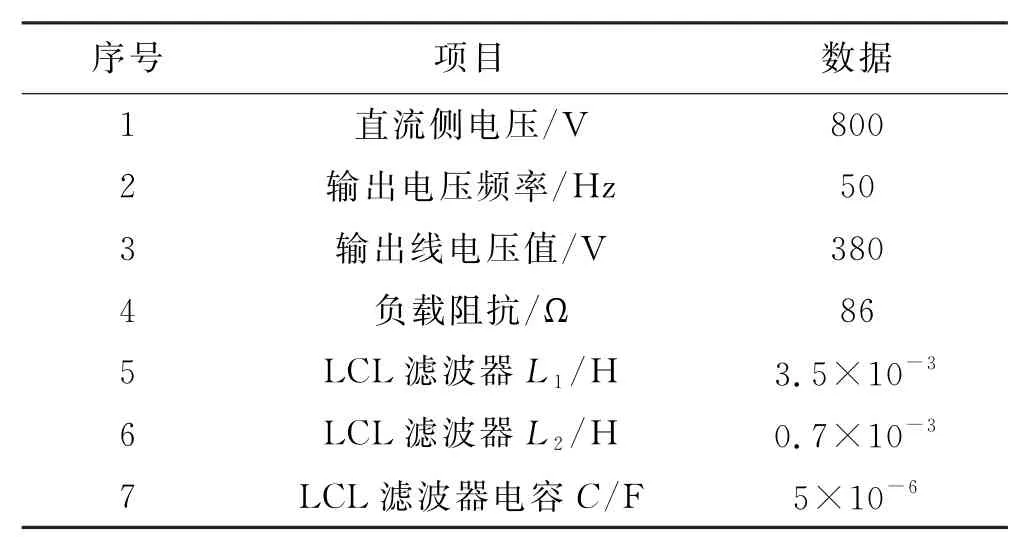
表2 仿真模型具体参数
3.1 单管故障
在0.06s时Sa1管开路故障,此时均方根电流值不相等,判断有故障发生,如图6(a)所示.与此同时A 相和B、C相电流平均值不为零,如图6(b)所示.


图6 Sa1 管0.06s开路故障
应用模糊规则,对故障特征进行辨识.如图7所示,辨识结果为1,对应模糊规则表为Sa1管故障.其诊断时间仅为0.008s,如图8所示.

图7 Sa1 管故障时模糊输出

图8 Sa1 管0.06s故障时模糊诊断输出结果
3.2 双管故障
双管故障分为同相双管故障和不同相双管故障[15].由于三相对称,本文的双管故障同相侧选择A相,不同相的双管故障选择A、B相.0.06s时,Sa2管故障和Sb3管故障,图9(a)所示为故障后的均方根电流值.从图中可以看出A、B、C 三相的均方根电流值不相等,判断发生了故障.图9(b)为故障后的电流平均值,从图中可以看出,故障发生后A,B两相电流平均值不为0,C相电流平均值接近于0.

图9 Sa2 管和Sb3 管0.06s故障
此时应用模糊规则,将三相电流平均值输入至建立好的模糊规则,辨识结果为16,如图10所示,根据模糊规则表即可识别出为Sa2管和Sb3管故障.双管故障从发生故障到诊断出故障用时仅为0.013s,如图11所示,为双管故障时的模糊诊断输出结果.

图10 Sa2 管和Sb3 管故障时模糊输出
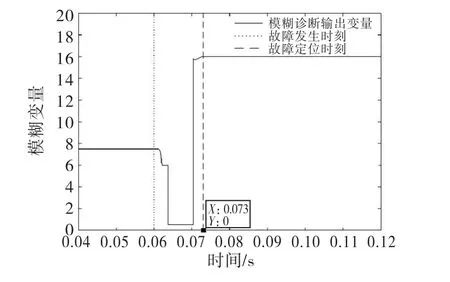
图11 Sa1 管和Sb3 管0.06s故障时模糊诊断输出结果
3.3 结果分析
以上实验表明,本文提出的基于模糊逻辑的三电平T 型逆变器故障诊断具有诸多优势.首先,在特征提取的时候,只需提取出逆变器输出侧的三相电流信号,无需增设额外的传感器.其次,本文的故障诊断将单管故障诊断时间缩短至0.008s,双管故障诊断时间缩短至0.013s.本文方法与相关方法的对比见表3.

表3 本文方法与相关方法的对比
4 结语
本文应用模糊规则,用均方根电流判别系统是否发生故障,用平均化后的电流值作为故障特征.实验结果表明:
1)将电流平均值模糊化后,通过建立的模糊规则,可使三电平T 型逆变器功率管的单管开路故障诊断时间降低至1/2基波周期内,双管开路故障诊断时间降低至3/4基波周期内.
2)该方法无需增设额外的传感器,无需设定诊断阈值,无需复杂的数据处理,仿真验证了所提诊断策略的准确性.

