基于数学学科核心素养的语言转译能力调查研究*
朱永厂
(江苏省无锡市辅仁高级中学 214123)
钱 铭
(江苏省无锡市第一中学 214031)
数学教育家斯托利亚尔曾指出:“数学教学也就是数学语言的教学.”[1]数学语言既是数学知识的重要组成部分,又是数学知识的载体,学习数学的目的就在于帮助学生运用数学的语言与自然进行更精确的对话.数学语言可分为文字语言、符号语言、图形语言三类.在高中数学教学过程中不难发现,学生对文字语言、符号语言和图形语言的理解和转译能力存在着较大差异和诸多不足,而这种差异恰恰体现了部分学生对数学本质理解的肤浅和数学核心素养水平的薄弱,这种不足更是反映了学生在情境与问题、知识与技能、思维与表达以及交流与反思等方面的欠缺,同时也反映了学生从数学的角度发现和提出问题、分析和解决问题能力[2]较弱.基于此,笔者认为在数学教学过程中注重数学语言转译能力的培养和均衡发展显得尤为重要.
1 测试问题的选择与编制
1.1 问题编制
为了调查高中生数学语言转译能力的现有水平和了解各种语言转译能力的差异,笔者经过精心设计编制出6道从不同方向测试语言转译能力的问题,并对江苏某重点高中高二和高三年级6个班(高二和高三各1个理科实验班、一个理科平行班和一个文科平行班,每班均为45人)270名学生做了关于数学语言转译能力水平及其差异的测试,旨在比较差异、寻找原因和研究策略.
问题1某饭店为了回馈顾客,推出如下活动:3个空汽水瓶可以换一瓶汽水.现有16个空汽水瓶,若不再交钱,最多可以喝瓶汽水,并谈谈你对问题的理解.
问题2某高校组织学生对所在区域的居民中拥有电视机、汽车、电脑等情况进行一次抽样调查.调查结果显示:有电视机的1 180户,有汽车的767户,有电脑的850户;电视机、电脑都有的598户,电脑、汽车都有的452户,电视机、汽车都有的520户;“三件”都有的285户.问:被调查的居民总户数为多少?
问题3请将图1用文字语言准确地告知你的同学,并写在后面的横线上:.

图1 图2

问题5在△ABC中,AB=AC,D为AC的中点,且BD=2,求△ABC面积的最大值.

1.2 设计意图
问题1和2是文字语言信息给予题,主要测试学生能否将文字语言的本质挖掘出来并将其转译为符号语言和图形语言,能有效地考查学生的数学抽象和逻辑推理等核心素养.问题3和4是图形语言信息给予题,主要测试学生能否将图形语言的本质表述出来并将其转译为文字语言和符号语言,问题具有一定的开放性,能够考查学生的思维与表达、交流与反思能力.问题5和6是符号语言信息给予题,主要测试学生能否将符号语言的本质概括出来,并将其转译为文字语言和图形语言,能够很好地考查学生的数学建模和直观想象等核心素养.
2 测试结果的现状分析
调查试卷采取独立闭卷答题,测试时间相对充裕,为35分钟,学生答题认真,信度较高,270份试卷全部有效.通过对试卷的认真批阅、分析和统计,制作出几份测试结果统计表.
2.1 具体问题的答题情况统计与现状分析

表1 具体问题测试结果分布表
由表1可知,问题1的正确率仅为29.26%,在这79人中得到正确结果8的大多数是用枚举法做出来的,只有33人能将关键信息“3个空瓶”换“1瓶汽水”的本质含义“2个空瓶换1个瓶中的‘汽水’”挖掘出来,如果题中的数字较大,枚举的难度就会加大,正确率会更低.
问题2的正确率为68.52%,有176人能够给出准确的过程,将文字语言转译为图形语言(Venn图)容易求解,记A={拥有电视机的居民},B={拥有汽车的居民},C={拥有电脑的居民},则A,B,C三个集合的元素个数分别为 1 180,767,850,两两交集的元素个数分别为598,452,520,三个集合的交集元素个数为285,因此居民总户数为1 180+767+850-(598+452+520)+285=1 512,正确率相对
较高.
问题3的正确率仅为18.52%,能够清楚表述的仅29人,能大概得其要领的有21人,其余的基本上是洋洋百言却越说越模糊,倘若你未曾见过该图形的话,根本不知其所言;而表达最巧妙的12位学生用的是坐标法,仅用一句话就表述得非常清晰:“在长宽为6×5的长方形网格内,顺次联结点(1,1),(5,1),(5,3),(4,4),(3,2),(1,4),(1,1)所得的封闭的图形.”



图3

由表1可知,问题1,3,5的正确率较低,即学生对文字语言向符号语言、图形语言向文字语言以及符号语言向文字语言的转译能力较低;而问题2,4,6的正确率相对较高,即学生对文字语言向图形语言、图形语言向符号语言和符号语言向图形语言的转译能力较高.
2.2 不同班级的答题现状与差异分析

表2 各班级测试结果分布表
由表2可知,高二、高三各层次班级正确率差异较大,高三理科实验班正确率最高,为61.11%,高二文科平行班最低,为30.37%,且理科生的正确率超过文科生,基本符合学生的认知特点和成长规律,随着高二学生认知水平的提高和训练的深入,各种能力会赶上或超过高三年级.
2.3 不同性别的答题现状与差异分析
由表4可知,男生、女生的正确率分别为49.28%,

表3 各班男女生人数分布表

表4 男女生测试结果统计表
35.86%,男生的数学语言转译能力优于女生,仅有问题3将图形语言向文字语言转译能力上男女生水平比较接近,说明女生的文字语言表达能力更有优势,这和男生的理性思维总体较强、女生的形象思维总体较强的认知规律是相符合的[3].
2.4 三种语言转译能力的现状与差异分析
测试结果中令我们感到惊讶的是,问题1是一道小学生都可以做的文字信息给予题,竟然难倒了这么多重点高中的优秀学生,表现出学生不善于捕捉问题的关键信息并将其本质合理转化;问题3的测试结果与我们的期望值相差很大,说明学生将图形语言转译为文字语言的能力很差,不知从何下手,说明语言表达能力还急待提高;问题5的测试结果也出乎我们的预料,说明学生将符号语言转译为文字语言的抽象概括能力较弱,而其他三种语言转译能力相对较好些,主要是当前的考试命题中多以这几种题型为主,教学中教师加强这方面的训练较多的缘故.这些都说明了当前数学教育中存在着诸多认识不足、功利思想比较严重等问题,这些问题都影响了数学学科核心素养的培养.
3 问题解决的对策研究
数学语言与生活语言不同的是数学语言具有较强的精确性、抽象性、严谨性和概括性.数学中的定义、定理、法则和公式等是通过文字、符号或图形语言的方式呈现出来的,换句话说,数学语言的表现形式便是数学知识的呈现方式.数学问题的解决、思维的培养和核心素养的形成都是建立在对数学语言的理解、转译和表达上的.三种语言特点的差异、不同学生个体的差异以及学生对不同数学语言理解的差异,使得学生之间数学语言转译能力存在着差异性和不均衡性[4].基于此,在数学教学中应做好如下几个方面.
(1)逐渐渗透“说数学”训练,培养思维与表达和交流与反思能力
著名心理学家维果茨基认为:数学语言和思维有着紧密的联系.在语言表达的同时,说背景,说内涵,说解法,说过程,通过大脑及时收集、整理相关信息,进而用语言表达出来,整个过程就是思维的理解到语言的过渡过程,通过“说数学”能够充分暴露学生对问题的理解过程,如此的学习方式加强了思维与语言之间的动态转译,有利于数学语言转译能力的培养[5].例如,在立体几何教学中,要让学生有更多说的机会,不仅要从图形语言到文字语言去说定理,还要从文字语言到符号语言去表述定理.
(2)加强文字语言抽象化和形象化训练,培养信息收集能力和数据分析素养

文字语言转译能力的培养关键是加强文字语言抽象化和形象化训练.这是一个长期的、潜移默化的过程,应从高一就开始培养,不能等到高三再进行突击和集训,也不能认为多做几道应用题就行了,必须在平常教学过程中坚持不懈地进行培养,要抓细水长流,要抓潜移默化,通过文字语言转译能力的训练培养学生信息收集能力和数据分析的素养.
(3)加强符号语言文字化和图形化训练,培养数学建模和直观想象素养
根据心理学的理论,人脑对信息的储存主要有语言和形象两种,但形象的容量应是语言的上百倍.所以,在某些方面,图形语言有符号语言所不能及的优越性.在数学教学中,在抓好形译数的同时,更要抓好数化形,使学生能将大量的符号语言迅速正确地转译成图形语言,借助图形直观形象的特点,进行观察、记忆、联想和分析来解决问题[7].比如,若对于不等式0≤x2+px+5≤1只有一个解,那么p的取值应该是多少?就这一问题,学生如果仅是抓住数学符号语言,就会觉得无从下手,思维就会受到限制,如果将其转译为图形语言:抛物线y=x2+px+5与图形0≤y≤1之间的位置关系,就可以使看似无法求解的问题轻松获解.
对于将符号语言转译为图形语言,在平时的教学中我们在意得很多,训练得也相对到位,几乎所有的数形结合思想的训练都集中在它身上.所以,这种能力的训练应讲究方法,不应靠题海来取胜.在教学过程中,如果图形不能准确地作出就会误导学生.为克服这一难点,可用计算机辅助教学,通过人机对话,使学生真正游刃于数形之间,提高其数化形的积极性.
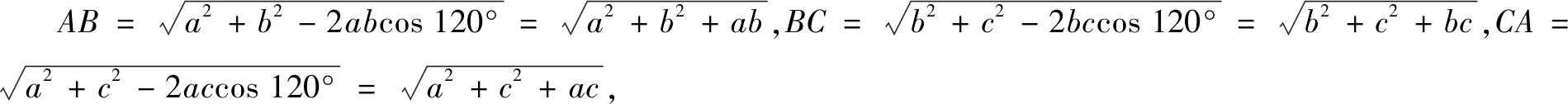

图4
当前,高中数学教学过程中对图形语言向文字语言转译重视不够,训练较少,学生处理此种问题的方法和能力还很欠缺,问题3的测试结果就是一个例证.
当然,文字语言、图形语言和符号语言是一个不可分割的、统一的整体,它们能够互相渗透、互相印证、互相转化和互相补充,从文字语言到符号(图形)语言的转译可使具体、复杂的问题形象化、简单化;从符号语言到图形(文字)语言的转译能使简洁、抽象的问题具体化、直观化;从图形语言到文字(符号)语言的转译能使直观的、模糊的问题符号化、精确化[8].数学教学过程中,要多让学生对同一个数学问题用多种数学语言进行表达,使他们能够从多角度、多方位去发现和提出问题、分析和解决问题.这样经常性的数学语言“互译”,一定能使学生的数学语言转译能力得到提高,从而实现培养学生数学核心素养的目标.

