变接触长度限制接触刀具车削不锈钢时的切削力及切削性能研究

庞学勤 邓文君 李松青

（华南理工大学机械与汽车工程学院，广东 广州 510640）

奥氏体不锈钢因其优异的耐腐蚀性能和无（弱）磁性而被广泛应用于石化工业、食品机械、航空航天、海洋工程和民用核电等领域。作为典型的难加工材料，其明显的加工硬化行为、低导热率以及相对较差的可加工性严重制约着它的加工效率［1］。尤其是在切削过程中会伴随大的热-力载荷，从而愈发恶化刀-屑界面的摩擦环境，导致严重的刀具磨损［2］。现已发现关于改善不锈钢加工性能的若干方法，如采用润滑措施［3］和设计刀具表面结构［4］等。然而，大量使用切削液会对环境和人身健康造成诸多伤害；对于新型润滑和冷却方法，大多数设备价格昂贵、难以操作且故障率高［5］。在表面纹理或微织构刀具的使用方面，若表面微结构设计不合理，反而会加剧刀具磨损［6］，增大切削力［7］并引起衍生切削现象［8］。有鉴于此，基于限制接触的刀具设计成为了实现高效加工的潜在有效方法。

与普通刀具相比，使用限制接触刀具在加工时可以减小切削力和摩擦系数［9］。Jiang等［10］发现，在限制接触模式的使用条件下，刀-屑接触面的摩擦力明显降低。Zou等［11］设计了一种新型限制接触槽刀，发现此种刀具在干加工Inconel 718合金时可以减小切削力，相比于普通刀具呈现出了更优异的抗磨损性能。一些学者也从理论分析的角度揭示了限制接触切削过程的合理性和可行性［12-13］。例如：Fang等［12］提出了限制接触切削滑移线模型以解释限制接触切削机理；Wang等［13］对通用滑移线模型进行修正，详细研究了限制接触的有关变量，考虑了应变、应变率和切削温度在滑移线场中的变化，证实了控制刀-屑接触长度能改善切削性能。

然而，目前已有的报道仅涉及接触长度恒定的限制接触刀具的研究，与变限制接触长度的刀具有关的研究鲜见报道。同时，有关限制接触刀具对奥氏体不锈钢的加工至今未见深入研究。基于变接触长度刀具更有利于车削加工这一事实，关于其切削力的分析、讨论以及相关切削性能的研究亟待开展。

文中从切削原理角度出发，通过理论分析及实验探讨了干环境下变接触长度限制接触刀具对AISI 316L奥氏体不锈钢切削性能的影响，提出基于非等分剪切区理论的半解析模型，以预测变限制接触条件下刀具产生的切削力。然后，对所提出的半解析模型进行深入讨论，并通过相关实验来验证模型的有效性，为证实变接触长度限制接触刀具对切削性能的改善提供理论依据。通过比较普通刀具、传统限制接触刀具和变接触长度的限制接触刀具对切削温度和刀具磨损的影响，从实验角度验证所设计刀具在实现不锈钢材料高效加工方面的可行性，以期为在切削难加工材料中新型刀具的设计提供参考依据。

1 变接触长度限制接触刀具的切削力建模

1.1 剪切变形区的分析模型

首先采用非等分剪切区模型（如图1所示）计算主剪切带厚度h，h可划分为不相等的两部分kh和(1-k)h［13］（其中k为剪切带不等分比）：

式中，hD为切削厚度，φ为剪切角。

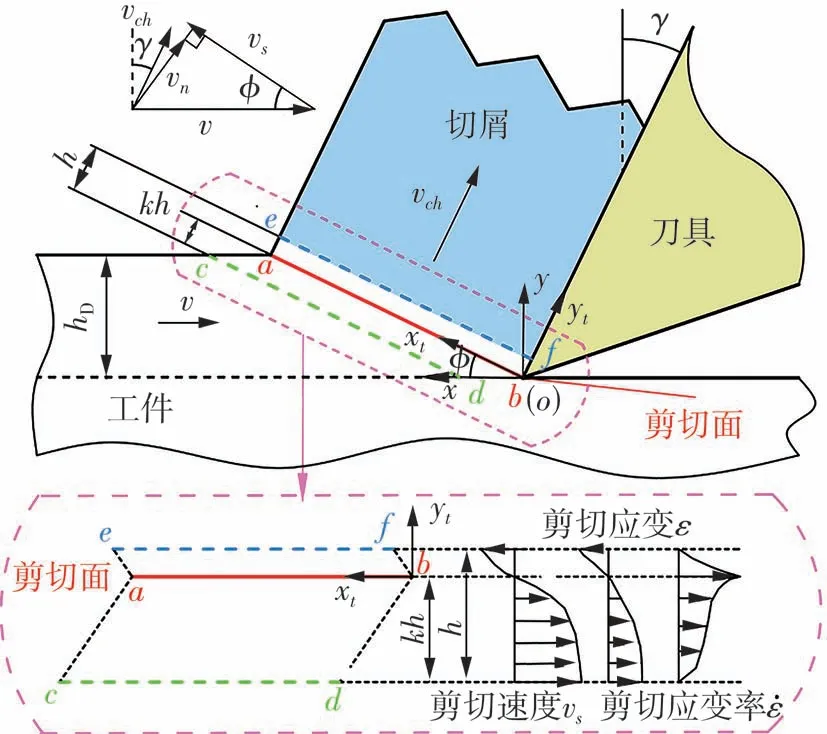
图1 非等分剪切区模型示意图Fig.1 Schematic diagram of the model of non-equidistant division shear zone

如图1所示，剪切区的入口边界和出口边界被认为是平行的。根据剪切速度vs与切削速度v的关系，剪切平面内法向速度vn可表示为

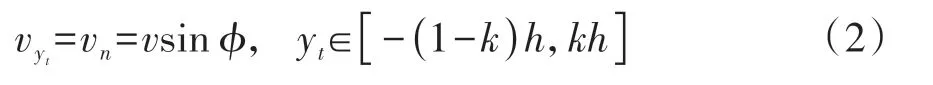
在非等距剪切区模型中，沿主剪切带的剪切应变ε和剪切应变率ε˙的分布如图1所示，其分别由式（3）和（4）表示：

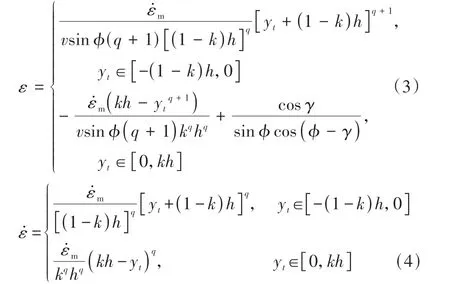
式中：γ为前角；为最大剪切应变率；q为主变形区切向速度的非均匀系数，其值等于3［15］。

由于切屑形成主要发生在第一变形区，因此ε˙m和k可由式（5）和（6）表示：

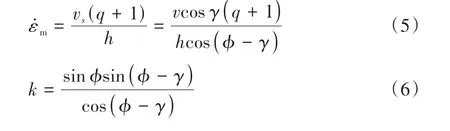
为了计算剪切流动应力，需要先确定主剪切面的瞬时温度。假设剪切变形区为主要热源，其瞬时温度T可由传递方程计算。由于主变形区的空间尺度有限，故扩散项可省略［13］。因此，传热方程可简化为只包括对流项和热源项：

式中，ρm为材料密度，cm为比热容，ϑ为泰勒-奎尼系数，τ为剪切流动应力。

将式（2）-（4）代入式（7）并积分，则非等分剪切区的瞬时温度可由式（8）计算：

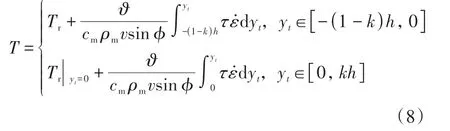
式中，Tr为室温，其值为25℃。

在非等距剪切区模型的基础上，采用Johnson-Cook本构模型确定主变形区中的剪切应力，该模型如式（9）所示：

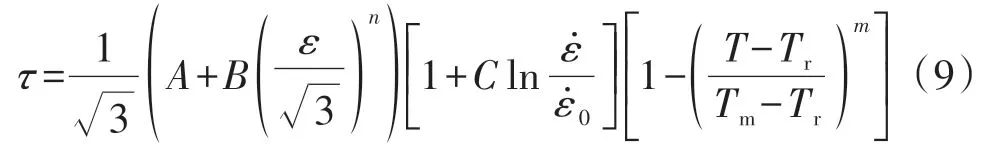
式中，A、B、C、n和m为J-C模型的参数，Tm为熔化温度。

综上所述，非等分剪切区内材料的热力演化可由式（3）、（4）、（8）和（9）确定，其中材料的应变、应变率和剪切应力的准静态分布可以通过求解上述公式获得。

1.2 变接触长度限制接触刀具在外圆车削中的切削力模型

根据金属切削最小能量原理［16］，剪切角φ和有效角ω之间的关系可由式（10）表示：

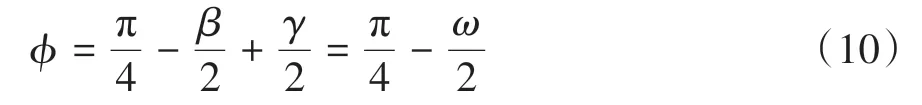
式中，β为摩擦角。

在使用限制接触刀具切削时，ω的值将取决于“受控”的刀-屑接触长度lc。相应地，ω可表示为lc的函数：

图2为非对称刀-屑接触区示意图，其中可变的刀-屑接触长度lc可由式（12）表达：

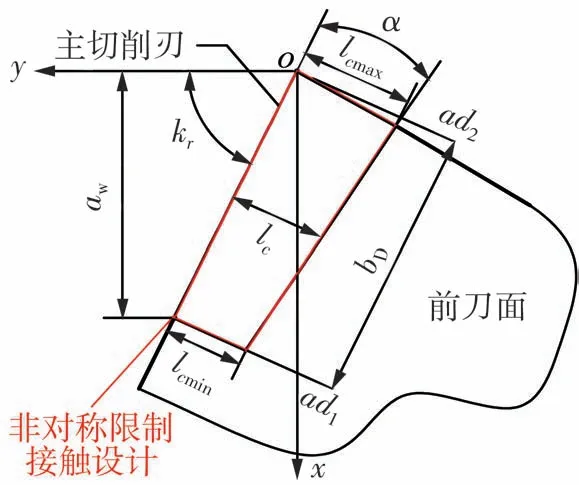
图2 变接触长度限制接触刀具的非对称刀-屑接触区示意图Fig.2 Schematic diagram of variable-length restricted contact tool with asymmetrical tool-chip contact area

式中，lcmax为最大刀-屑限制接触长度，α为限制接触角，kr为主偏角。

将式（11）代入式（12），则ω可表示为在笛卡尔坐标系中关于x的函数：

基于斜角自由切削模型和离散化原理，限制接触刀具的切屑形成力分量Fx可通过式（14）由fx沿x方向积分计算。类似地，Fy和Fz可由式（15）和（16）计算：

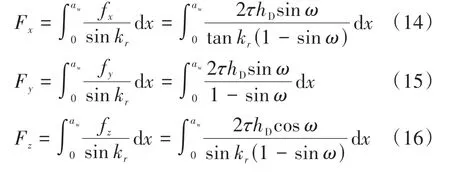
式中，fx、fy和fz分别为切削刃上沿x、y和z方向的单位切削力。

图3 为变长度限制接触刀具外圆车削的切削力模型。由于刀尖钝圆半径的存在，副后刀面会产生额外的切削力分量，记为Fta。因此，限制接触刀具上的切削力分量可由式（17）-（19）表示：

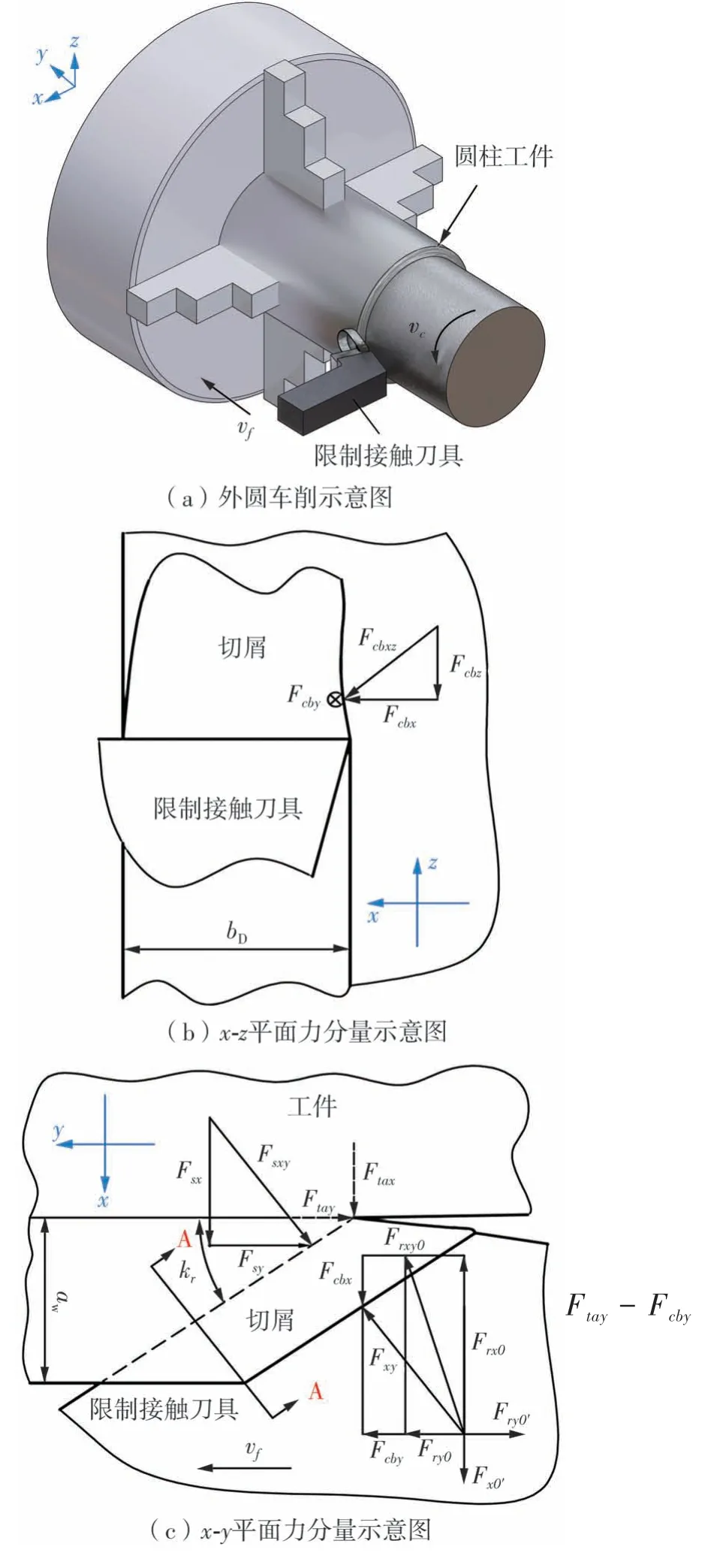
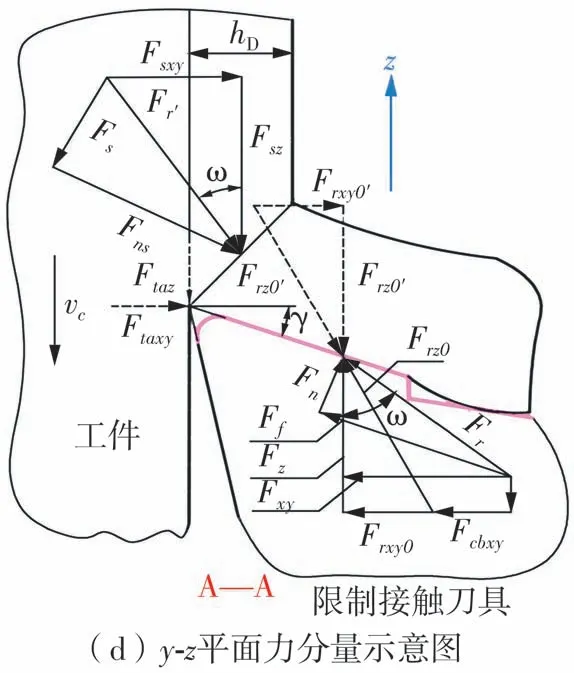
图3 变接触长度限制接触刀具外圆车削的切削力模型Fig.3 Cutting force model of variable-length restricted contact tool in cylindrical turning process

式中，Frx′、Fry′和Frz′分别为前刀面上沿x、y和z方向的力分量，Ftax、Ftay和Ftaz分别为副后刀面上沿x、y和z轴方向的力分量。

作用在副后刀面的反向额外力可记为Fcb，其在切屑上产生的力分量可由式（20）-（22）表示：

式中，Fcbx、Fcby和Fcbz分别为Fcb沿x、y和z方向的力分量。

根据单位切削力分量和剪切平面切削力分量之间的关系，剪切平面沿x、y和z方向的力分量Fsx、Fsy和Fsz可分别由式（23）-（25）计算：

式中，aw为切削深度。

由于Frx′和Frx是等大反向的作用力，故式（17）-（19）可转换为式（26）-（28）：

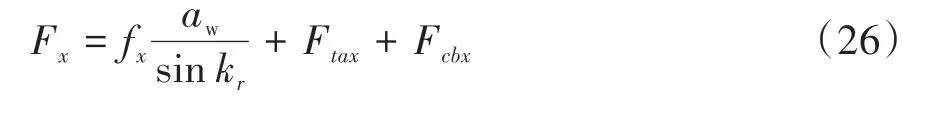
理想条件下，刀具被认为是绝对锋利的，但实际情况下会存在刀刃钝圆半径，因此，切削过程中的总切削力应视为由两种力分量的矢量叠加构成，即切屑形成力和犁耕力［17］。将Pl、Pt和Pc分别定义为沿x、y和z方向的犁耕力（详细计算见附录A），将Ftax+Fcbx、Ftay-Fcby和Ftaz+Fcbz分别定义为∑Ftcx、∑Ftcy和∑Ftcz，则单位切削力fx、fy、fz和力分量∑Ftcx、∑Ftcy、∑Ftcz可通过总切削力FX、FY和FZ表示：

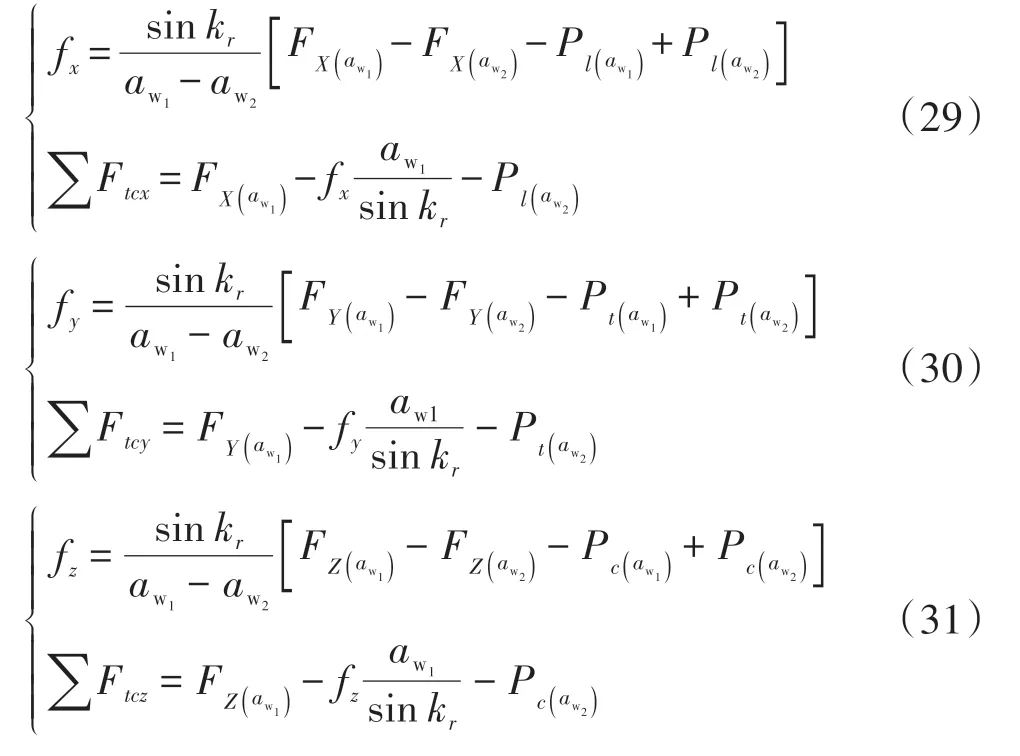
式中，下标aw1和aw2表示不同的切削深度，其中aw1＞aw2。

因此，在变长度限制接触刀具的外圆车削过程中，FX、FY和FZ可由式（32）-（34）计算：

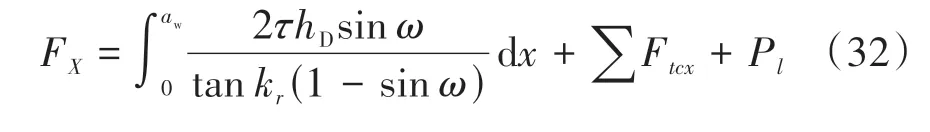
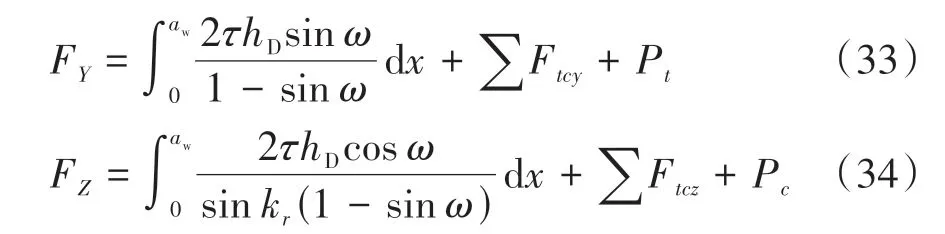
变接触长度限制接触刀具所产生的切削力分量的表达式已在式（32）-（34）中示出，但是由于其中的微分单元力无法直接计算，所以∑Ftcx、∑Ftcy和∑Ftcz无法以解析计算的方式确定；同时，ω是关于刀-屑接触长度的函数，由于实际刀-屑接触长度与切削参数、材料属性密切相关，故ω无法用定性的方法精确计算。因此，式（32）-（34）只是限制接触条件下切削力预测模型的一般表达式，要确定切削力与刀-屑接触长度之间的关系，还需进一步的实验验证。鉴于上述问题，下文将通过大量的车削实验，对变接触长度的限制切削过程的切削力模型进行讨论和验证。

2 实验方案

2.1 限制接触刀具的制备以及工件材料

限制接触刀具以无涂层硬质合金刀片YG 6为基体，材料的物理性能如表1所示。限制接触形状采用线切割和微电火花相结合的加工方法制成，限制接触图形的误差范围为±20μm。图4展示了常规限制接触刀具和文中设计的变接触长度的限制接触刀具，即矩形限制接触刀具（Rectangular-Pattern Restricted Contact Tool，RRCT）和梯形限制接触刀具（Trapezoidal-Pattern Restricted Contact Tool，TRCT）。其中，对于梯形限制接触刀具，最大限制接触长度lcmax和限制接触角α为其参数。

表1 硬质合金（WC-6%Co）刀具的物理和机械性能Table 1 Physical and mechanical properties of cemented carbide（WC-6%Co）tool

工件材料采用AISI 316L奥氏体不锈钢，其化学成分、Johnson-Cook本构参数、热-物理性能如表2-4所示。该材料属于面心立方结构，同时微观组织里面存在再结晶孪晶和等轴奥氏体晶，其结构如图5所示。

图4 常规矩形限制接触刀具和变接触长度的梯形限制接触刀具Fig.4 Conventional rectangular-pattern restricted contact tool and variable-length trapezoidal-pattern restricted contact tool

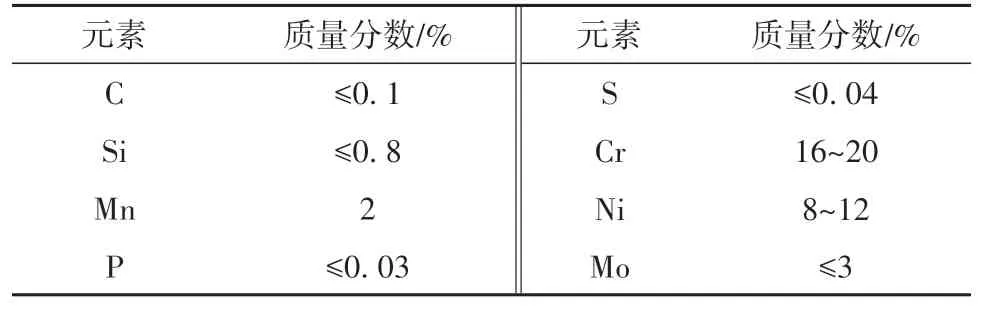
表2 AISI 316L奥氏体不锈钢的化学成分Table 2 Chemical composition of AISI 316L austenite stainless steel

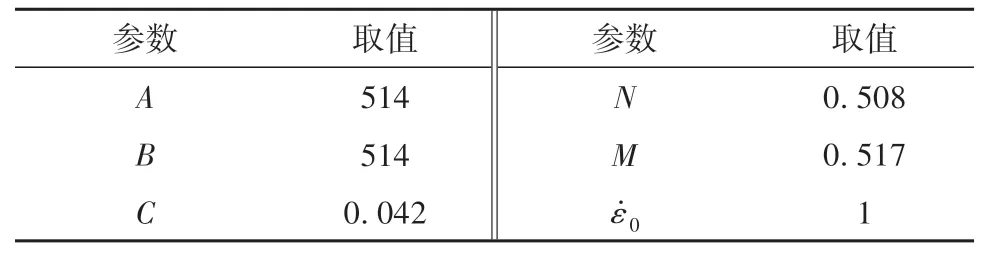
表3 AISI 316L奥氏体不锈钢的Johnson-Cook本构参数Table 3 Johnson-Cook constitutive parameters of AISI 316L austenite stainless steel

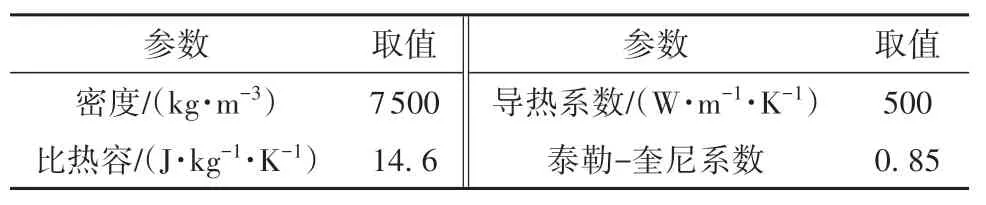
表4 AISI 316L奥氏体不锈钢的热-物理性能参数Table 4 Thermophysical property parameters of AISI 316L austenite stainless steel

图5 AISI 316L奥氏体不锈钢的显微组织Fig.5 Microstructure of AISI 316L austenitic stainless steel

2.2 实验设计

普通平面刀具（Conventional Tool，CT）、RRCT和TRCT的几何参数如下：限制接触宽度W=2mm，前角γ=0°，后角α0=8°，主偏角kr=90°，副偏角k′r=2.5°，刃倾角λs=0°。所有实验均在干切削条件下进行，具体实验步骤分为3个阶段。

第1阶段切削速度v=79.2 m/min，进给率f取0.12 mm/r和0.20 mm/r，切 削深度aw取1 mm和2 mm。使用RRCT，lc为0.2～1.5mm，每组实验重复3次。本阶段实验的目的是观察和讨论切削力与限制接触长度的关系，同时确定参数∑Ftc和ω=G(lc)。

第2阶 段v=79.2 m/min，f取0.12 mm/r和0.20 mm/r，aw=2 mm。使用TRCT，lcmax取0.3 mm和0.4mm，α取4.8°和7.2°。本阶段实验的目的是验证所提出的半解析模型。

第3阶段使用CT、RRCT（lcmax=0.4 mm）和TRCT（lcmax=0.4 mm，α=7.2°），在固定的材料去除量下进行试验（v=79.2m/min，aw=2mm，f=0.20mm/r，切削时间为3min）。此阶段实验的目的是分析和比较不同刀具对切削温度和刀具磨损的影响。

需要指出的是，文中加工参数的选择是根据相关加工手册、参考文献以及前期大量实验所确定的［19-20］。

2.3 实验设备与测量仪器

实验在C6140A1车床上进行，图6展示了相关的实验设备与测力测温仪器。其中，切削力由Kistler 9257A型压电测力计测量，切削温度由Fluke Ti-200型红外热成像仪测量（切削实验进行到120 s时进行温度测量）。此外还借助Quanta200型扫描电子显微镜（Scanning Electron Microscope，SEM）和能谱仪（Energy Dispersive Spectrometer，EDS）观察、分析刀具的磨损状态。

图6 实验装置Fig.6 Experimental setup

3 结果与讨论

3.1 切削力分析

3.1.1 变接触长度限制接触刀具切削力公式的讨论

图7为RRCT在不同进给率和不同限制接触长度下的切削力变化趋势。由图可知：在不同的进给率下，当限制接触长度大于某一值后所测得的主切削力FZ和进给力FY几乎不变；当lc分别小于0.6mm和0.8 mm时，FY和FZ均随着lc的减小而减小，且FY的减小速率比FZ的快。此结果表明，随着lc的减小，ω是动态变化的，而非固定值。

根据式（29）-（31）和图7数据对∑Ftcx、∑Ftcy和∑Ftcz进行计算，得：当f=0.12mm/r时，∑Ftcx、∑Ftcy和∑Ftcz的平均值分别为97.3N、153.4N和248.9N；当f=0.2 mm/r时，平均值分别为145.7 N、208.2 N和292.4 N。由式（11）-（13）可知，ω是关于lc的函数，其变化呈两种分布模式，如图8所示。当lc小于某一临界值时，ω与lc呈线性关系；当lc大于某一临界值后，ω基本保持不变，表明此时lc对ω的影响很小，在这方面限制接触刀具与普通刀具基本没有差别。为了便于讨论，将ω的角度单位转换为弧度（rad），并进行函数拟合，拟合后可表示如下：

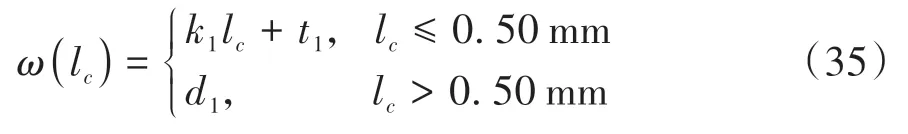
式中，k1=0.1833，t1=0.5253，d1=0.622。

当f=0.20 mm/r时，拟合后的ω(单位：rad)和lc之间的关系可由式（36）表示：

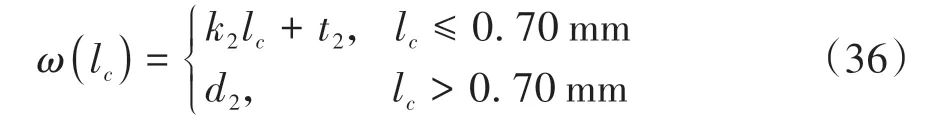
式中，k2=0.1367，t2=0.498，d2=0.596。

如图8所示，当f为0.12 mm/r和0.20 mm/r时，函数拐点值分别为0.5和0.7左右。相应地，切削力公式（32）-（34）修正为式（37）-（42），如下所示，当lc小于拐点时，FX可由式（37）表示（其详细推导过程见附录B）：

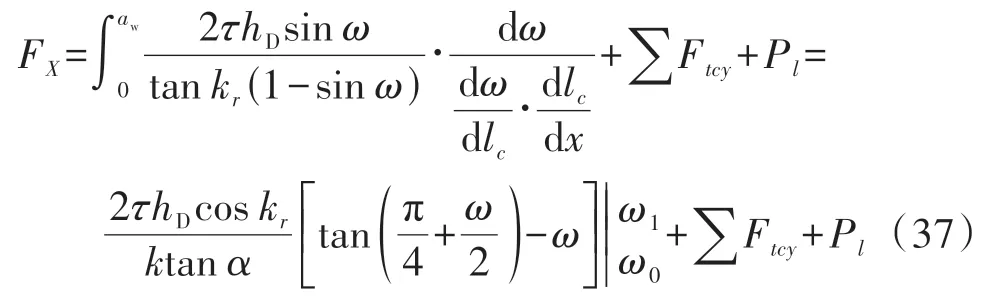
进给力FY和主切削力FZ则由式（38）和（39）表示（其推导方法可参考附录B）：

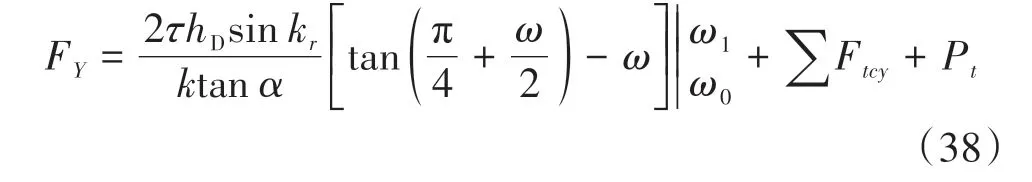
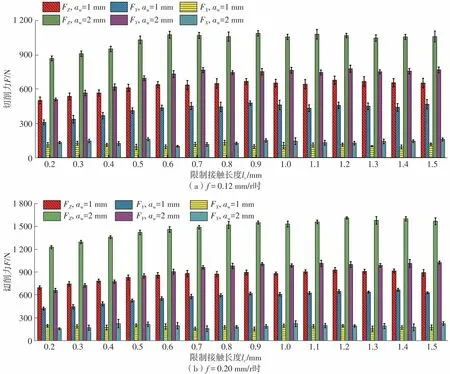
图7 不同进给率下切削力随lc和aw的变化Fig.7 Variation of cutting force with lc and aw under different feeds

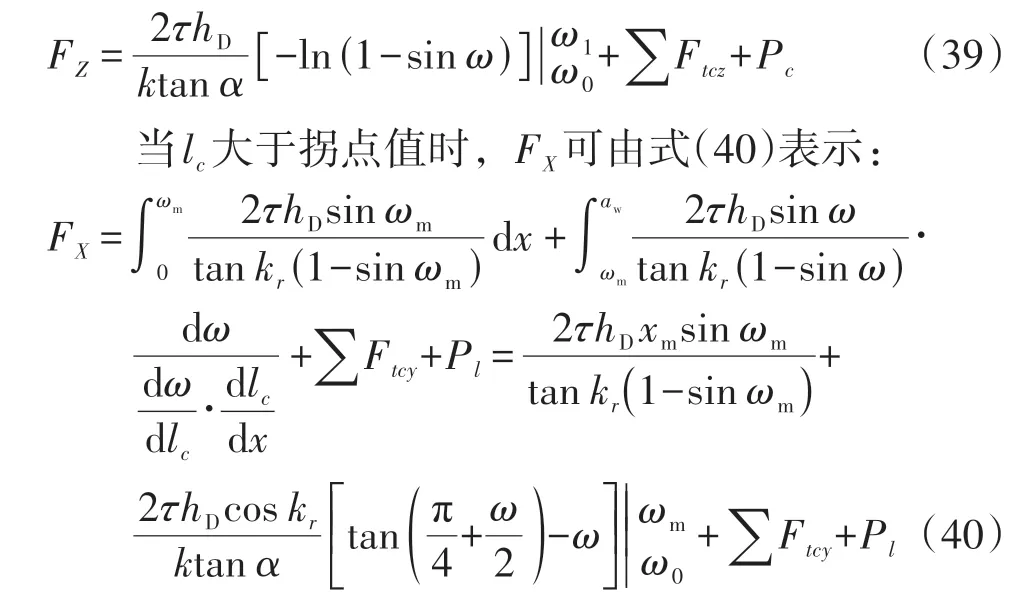
进给力FY和主切削力FZ则由式（41）和（42）表示：

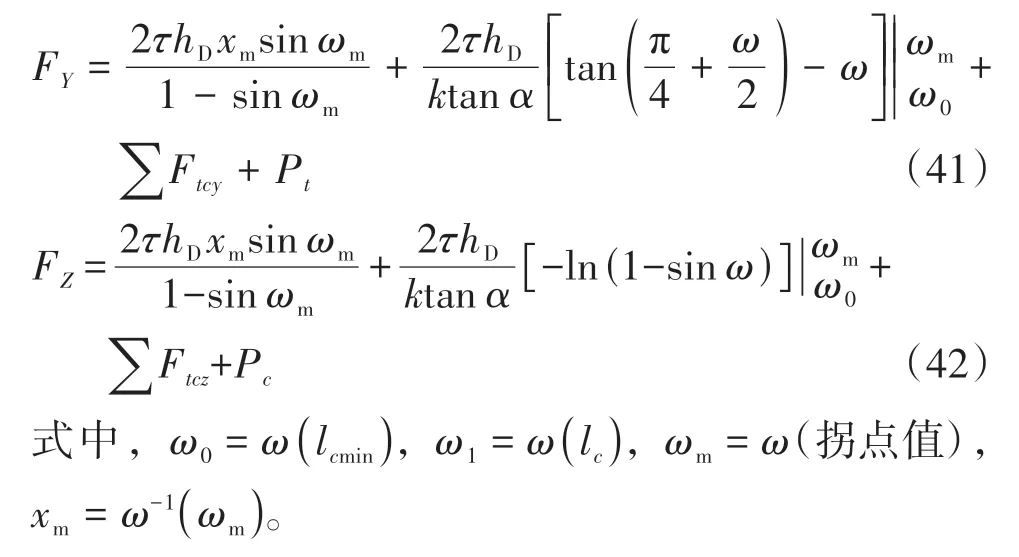
由式（37）-（42）可知，由于在该半解析模型中须考虑限制接触长度与拐点之间的关系，因此切削力预测公式应分为两部分讨论。由于第二变形区以及工件材料的本构属性在不同的加工参数下均是动态变化的，通过实验确定的拐点位置将比理论分析值更精确，这一点已得到相关文献［21］的证实。1.1节所提出的非等距剪切区模型正是基于这一观点考虑了工件材料的属性，因为工件在其任何强度特征在没有相对应的应变时，其应力特征不能被单独考虑［22］。通过大量实验获得的函数关系式ω=G(lc)也正是考虑了实际的加工参数对刀-屑接触长度的影响。此外，所提出的预测切削力方法还有一个优势，就是可以解决实际刀-屑接触长度变化过程中因前刀面上应力变化而导致的滑移线场改变。这种通过大量实验来确定ω的方法可以回避前刀面上应力改变的问题［12］，且巧妙解决了粘结摩擦和滑移摩擦之间的转换或变化对切削过程的影响［23］。此半解析切削力模型也正是基于上述观点而提出的。

图9为所提出的半解析模型的计算流程图，该模型可用于预测非恒定刀-屑限制接触长度下的切削力。首先根据所给定的切削参数和材料性能，通过不等分剪切区模型求解出剪切流动应力τ；其次建立有效角ω与非恒定限制接触长度lc之间的关系式；然后对切屑形成力进行建模，推导出外圆车削时所产生的力分量；最后通过大量实验求解出ω与lc的函数关系，并讨论切削力开始改变的拐点位置，求解出变限制接触长度刀具所产生的切削力的预测公式。

3.1.2 变接触长度限制接触刀具切削力公式的验证

文中提出的变接触长度的限制接触刀具能有效减小切削力，相比于RRCT，其刀-屑接触界面会进一步缩小，进给力和主切削力也将更大程度地减小。当切削深度为2 mm、进给率为0.12 mm/r和0.20 mm/r时，对应的剪切流动应力分别为569.7 MPa和510.3 MPa。表5所示为新设计的限制接触刀具所产生的切削力的实验和预测结果，由表可知，所提出的半解析模型能够很好地预测进给力FY和主切削力FZ，实验值与预测结果的最大误差不超过13.97%，证明了将刀-屑接触长度与切削力分量相关联的合理性和准确性。另一方面，观察到预测值与实验测量所获得的FX之间存在较大误差，这可能是由于在切削过程中，此方向上产生了轻微的刀具颤振现象，致使FX的实际测量结果偏大，导致预测的百分比误差偏大。

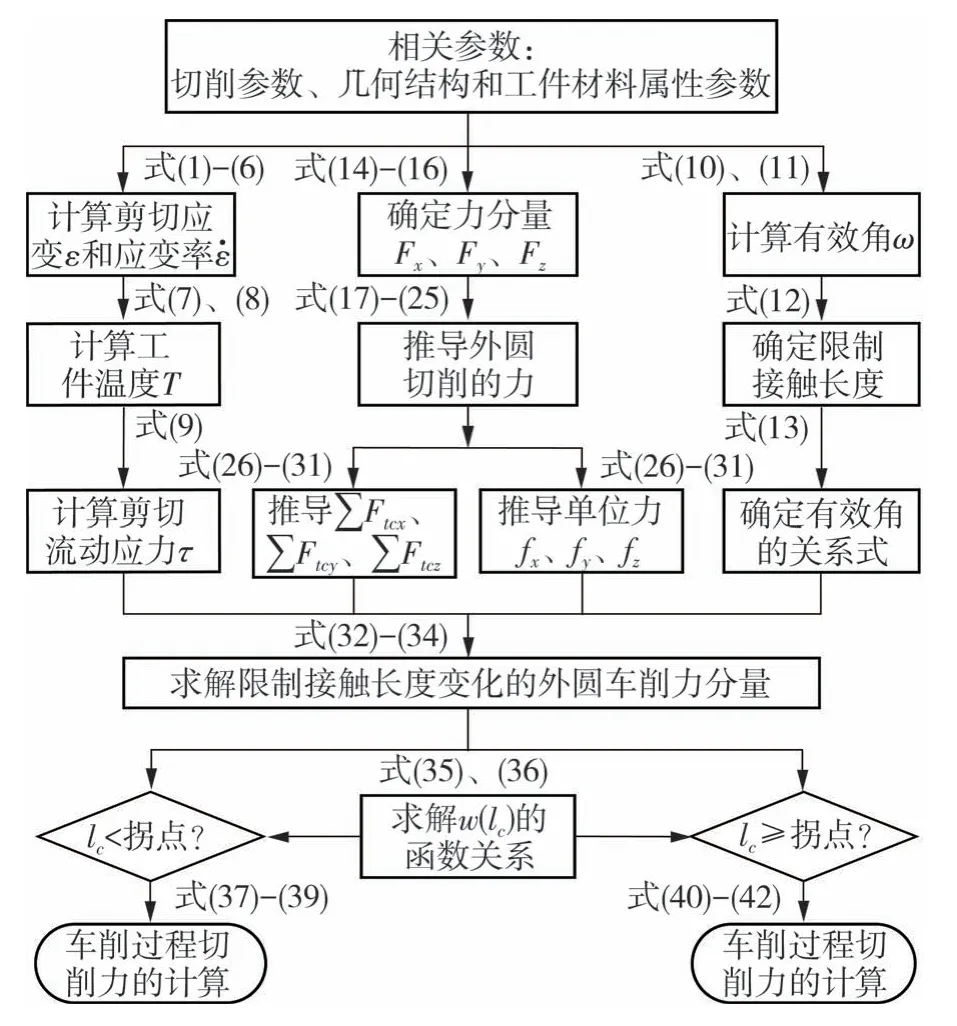
图9 变接触长度限制接触刀具的切削力预测流程Fig.9 Flow chart for evaluating the cutting forces of variablelength restricted contact tool

表5 TRCT实验和预测的切削力的比较Table 5 Comparison of experimental and predicted cutting forces of TRCT

3.2 切削温度分析

图10展示了CT、RRCT和TRCT在切削过程中加工区域的温度分布结果。由图可知，在CT刀尖附近存在较大的高温区域。相比之下，限制接触刀具所产生的高温区域明显减小。其中，CT、RRCT和TRCT的最高切削温度依次为271.7、229.3和194.8℃。相比于CT和RRCT，TRCT的最高温度分别下降了28.3%和15.05%。这得益于变接触长度的限制接触结构能进一步减小刀-屑接触区域，降低切削力及缓解刀屑-界面间的摩擦，从而降低切削温度。此外，由于在流动切屑和限制接触结构之间存在非封闭的传热空间，此空间内的空气间隙也能促进空气流动，进而降低切削温度。这是因为当开放式空腔形状不一致时，产生的压差有利于促进空气动力润滑和散热［24］。根据文献［25］关于空腔结构对湍流影响的研究结果，非封闭非均匀型腔会引起不完全涡流和明显涡旋。当象征湍流开始形成的不完全涡流和象征湍流发展的涡旋出现时，空腔的冷却性能和对流传热性能均会显著增强，这将有助于刀具在加工环境下的自冷。因此，TRCT能比RRCT更高效地降低切削温度。

图10 不同刀具切削过程中的红外热成像结果Fig.10 Infrared thermography results of different cutting tools

图11 CT前刀面磨损情况的扫描电镜图和相应的EDS分析结果（切削时间3min）Fig.11 SEM images and corresponding EDS analysis results of worn rake face of CT with a cutting time of 3min

3.3 刀具磨损分析

图11 展示了CT前刀面磨损的SEM图像以及对应的EDS分析结果。从图11（a）和11（b）中可以观察到，前刀面上出现了严重的月牙洼、刀刃崩碎和工件材料粘附现象。从图11（d）可以发现，已磨损的前刀面上出现了磨屑和磨粒磨损痕迹，这表明磨粒磨损是刀具的磨损形式之一。此外，严重的材料粘结行为还导致了积屑瘤的形成（见图11（c）），当积屑瘤达到某一尺寸极限时，它会随着切削过程的进行而破裂。如图11（e）所示，积屑瘤的形成与破裂严重影响了刀具的完整程度，会使切削刃随材料粘附层的散裂而剥落，最终导致刀刃损坏。

图12显示了RRCT前刀面磨损的SEM图像。相比于CT，在图12（a）中RRCT前刀面的磨损程度明显降低。尽管仍存在材料粘结和刀刃崩碎现象，但与CT相比已有明显改善。由图12（b）-12（d）可知，刀具材料的剥落行为仅发生在局部限制接触区域，且并没有持续扩大发展为月牙洼。这一现象说明限制接触结构的存在能缓解刃崩碎和月牙洼的形成。相比于CT，限制接触模式能减少积屑瘤的形成，并增强刀具的抗磨损性能。

图13展示了TRCT前刀面磨损的SEM图像。在图13（a）和13（b）中，没有观察到月牙洼和崩刃现象，而在图13（c）中仅观察到少许刀具材料剥落行为，表明变限制接触长度设计能有效抑制刀具材料剥落的发生。与传统限制接触结构相比，新设计的结构能有效缓解由材料粘结诱发的刀刃破损和刀具材料剥落现象，意味着TRCT通过进一步减小刀-屑接触界面的方式更有效地抑制了切削过程中热-力载荷对刀具的影响。

图12 RRCT前刀面磨损情况的扫描电镜图（切削时间3min）Fig.12 SEM images of worn rake face of RRCT with a cutting time of 3min

图13 TRCT前刀面磨损情况的扫描电镜图（切削时间3min）Fig.13 SEM images of worn rake face of TRCT with a cutting time 3min

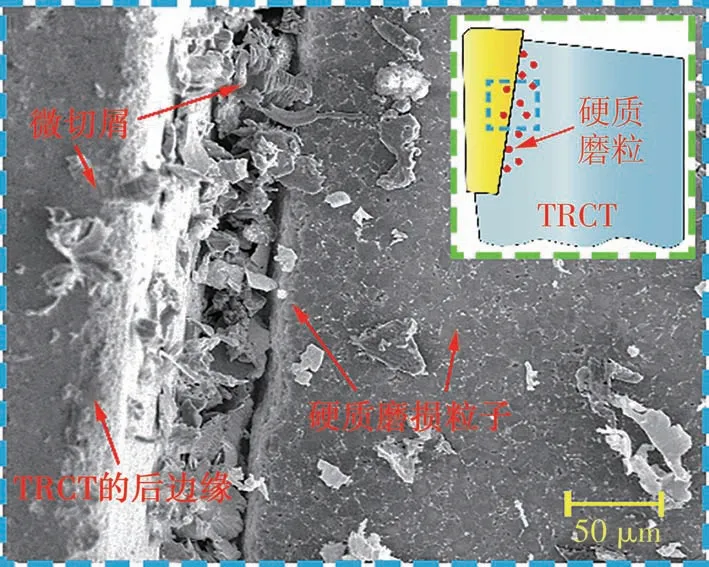
图14 限制接触结构处对磨粒和磨屑的收集作用Fig.14 Collection of abrasive particles and microchips by restricted contact structure

通过对AISI 316L不锈钢干切削过程中刀具磨损形貌和元素成分的分析发现，CT的磨损形式主要为粘结磨损和磨粒磨损，这与Szczotkarz等［26］的研究结果一致。而对于限制接触刀具来说，粘结磨损则为其最主要的磨损形式，虽然在已磨损的前刀面上观察到了硬质磨粒的存在（见图13（b）），但无明显可见的磨粒磨损痕迹。当使用不同刀具进行了相同时间的切削后，可以发现CT切削表面出现严重的刀刃崩碎、月牙洼以及明显的切削刃崩碎破损行为，同时伴随着清晰的磨粒磨损痕迹。在RRCT上则只出现局部崩刃区以及月牙洼形成前兆的刀具材料剥落现象。相比之下，在TRCT上没有出现任何崩刃现象以及刀具材料剥落区。在这种情况下，前刀面抗磨损性能的提高将减少后刀面的磨损，从而延长刀具使用寿命［26］。

基于前述分析及刀具磨损结果对比，可以发现，当引入变接触长度的限制接触设计后，TRCT的切削性能较CT和RRCT有所提高，且切削表面的磨损程度显著降低。根据文献［27］的分析，实际刀-屑接触区域的减小将抑制热-力载荷对刀具的不利影响，有助于减缓材料的粘附趋势，并提高刀具的抗粘结性能。此外，变限制接触长度的结构能进一步减小潜在的磨粒磨损区域，且该结构还能提供类似微沟槽一样的储存硬质磨粒的功能［7］（如图14所示），这将显著减小硬质磨粒对前刀面的耕犁破坏作用，抑制磨粒磨损行为。相应地，在引入变限制接触长度的设计后，所研制刀具的抗磨损性能将得到显著提升。

4 结论

文中设计和制造了一种变接触长度的限制接触刀具，提出了非恒定接触长度的切削力预测模型，并对切削温度和刀具磨损进行了研究，以揭示普通平面刀具、常规限制接触刀具和所开发刀具在干加工AISI 316L奥氏体不锈钢时的性能差异，主要工作及相关结论如下：

1）文中利用非等分剪切区模型和统一切削力学理论，建立了变限制接触长度刀具的半解析切削力预测模型，该模型考虑了材料热力学行为、刀具几何结构以及加工条件，预测结果和实验数据具有较好的一致性，可用于限制接触结构刀具的切削力分析，为评估刀具参数在实际切削中的可行性提供了有效途径；

2）对比普通刀具与限制接触刀具后发现，变接触长度的限制接触刀具在干切削时能改善切削性能，所设计的限制接触刀具能进一步减小切削力与切削温度，相比于CT和RRCT，TRCT的最高温度分别下降了28.3%和15.05%；除了进一步减小刀-屑接触区域将有助于减少切削热外，变限制接触结构还能增加散热并促进刀具自冷，进而降低切削温度；

3）变限制接触结构能提高刀具的抗磨损性能——限制接触结构不仅可以减小潜在的磨粒耕犁区域，而且能收集和储存硬质磨粒，从而减少刀具的磨粒磨损；另外，变限制接触长度的刀具可通过进一步减小刀-屑接触区域，更大程度地减少热-力载荷和冷焊过程，进而更有效地缓解切削刃破损和刀具材料的剥落行为。

附录A：

根据WALDORF提出的车削犁耕力模型来描述犁耕力分量，其中犁耕力分量由下式确定：

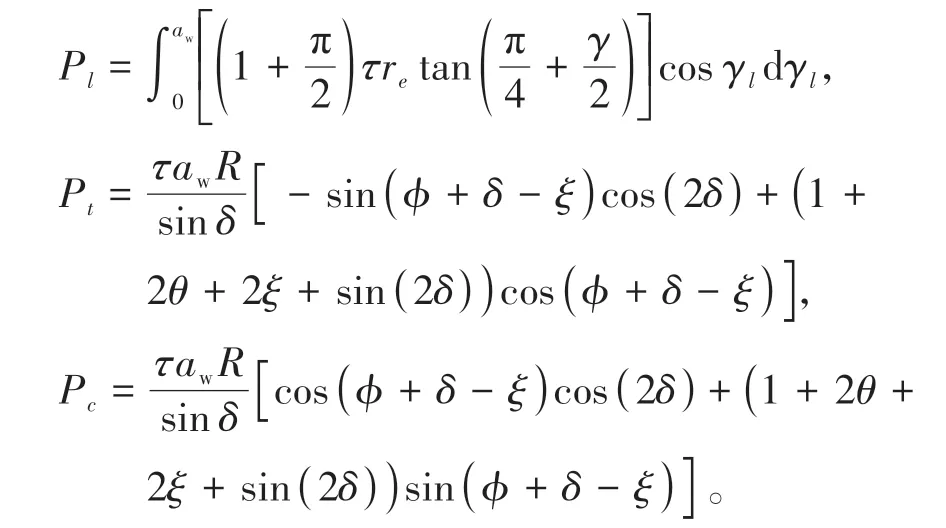
式中，R，δ和ξ和是半圆形和滑移线场的相关参数，可从文献［17］获取。

附录B：

关于预测变接触长度限制接触刀具产生的切削力分量FX，当lc小于拐点时（见式（37）），其详细推导过程如下：

关于进给力FY和主切削力FZ的推导过程参见上述FX的推导步骤，此处不再赘述。