大展弦比等剖面多段折叠翼颤振特性
田素梅, 张应鹏, 张贺铭, 祁武超
(1.沈阳航空航天大学 航空发动机学院, 辽宁 沈阳 110136;2.沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室, 辽宁 沈阳 110136)
0 引言
为降低能源需求,高空长航时无人机通常采用大展弦比方案以追求高的升阻比。然而,随着翼展的增大,机翼结构固有频率会发生相应地降低,呈现出“长且柔”的特点,导致大展弦比无人机通常具有较低的颤振速度,且翼尖容易发生扭转颤振。当飞行任务改变导致飞行速度增加,例如被追击时,机翼较低的颤振速度将成为其成功逃脱的限制因素。另一方面,由于无人机结构形式的特殊性,常采用空中投放的方式进行起飞作业,较长的翼展会对装载空间提出很高的要求,尤其是无人机在需要完成集群作业时,单次投放的无人机数量会受到空间限制。一种解决方案是通过结合适当的铰链几何结构,在飞行过程中将大展弦比机翼进行折叠和展开一定的角度以期获得更好的飞行和操纵性能。
2009年,Sebastian等[1]建立了一种气动弹性模型用于求解两段均匀折叠机翼的颤振解析解,可通过调整该模型所设置的参数以观察颤振解的变化,结果显示,内侧机翼和外侧机翼之间的折叠角对于两段折叠翼的气动弹性行为具有重要影响。2010年,Attar等[2]研究了由机身、内侧机翼和外侧机翼组成的折叠机翼结构非线性气动弹性效应,结构部分采用冯卡门几何非线性动力学理论建模,而气动模型则使用三维涡格法进行描述;将计算模型结果与风洞试验结果进行了对比发现,极限环振荡幅度和理论的主响应频率结果相吻合;并且,具有最大外侧折叠角的折叠机翼在极限环振荡时翼尖位移要高于其他两种配置。2011年,Wang等[3]基于梁理论提出一种预测多段折叠翼固有频率的计算方法,结构模型通过在各段机翼之间添加约束条件得到,并基于Lagrange方程得到系统动力学方程,其将理论分析结果与试验进行了对比,在分别考虑2段、3段、4段模型的情况下误差不超过10%。Zhao等[4]研究了在不同参数配置下的折叠翼颤振特性并提出一种参数化气动弹性模型,结构部分是在子结构综合的基础上建立,而气动力模型采用偶极子格点法得到,算例结果显示折叠翼的颤振特性对折叠角度是敏感的,随着折叠角的增加会发生模态迁移的现象。Zhao等[5]还采用一种浮动框架法建立了一组控制折叠翼变形过程中随时间演化的微分代数方程组,并计算了机翼变形过程中的瞬态响应,其所建立的方程组可以与计算流体力学(CFD)程序集成以对折叠机翼进行瞬态气动弹性分析。
2016年,Hu等[6]考虑了折叠翼在变形过程中的气动弹性现象,折叠翼结构使用柔性多体模型化,并通过偶极子格网法得到气动影响系数矩阵;结果显示折叠过程和展开过程对气弹稳定性有着相反的影响。同年,Castrichini等[7-8]研究了在飞行中利用折叠翼梢作为减少动态阵风载荷效应的装置,其引入了被动非线性铰链弹簧,仅在较大载荷情况下允许翼梢发生偏转,结果表明,这种铰链弹簧装置对减少阵风载荷具有显著效果。Yuan等[9]研究了飞行器折叠椅在低空高速展开的过程,这一过程伴随有非定常流动,为了准确模拟非定常流动中的移动边界问题,采用具有重叠非结构多面体网格的非定常CFD方法计算气动力,得到的结构展开角度和角速度可用于机翼展开机构的设计过程。Hu等[10]研究了具有立方刚度非线性折叠机翼的气动弹性特性,折叠翼的结构模型由拉格朗日方程描述,同时使用偶极子网格法计算不同折叠状态下的气动影响系数矩阵,并引入Kriging代理模型技术将系数矩阵插值为有理函数。具有立方刚度的折叠翼气动弹性响应表明,折叠翼的变形过程对初始条件和折叠角是敏感的。范国芳等[11]针对飞行器翼面的高速展开过程,采用和非定常两种方法对折叠翼面展开过程气动载荷进行分析研究;研究发现,当翼面展开速度与来流速度相近时,展开过程的非定常效应不可忽略而必须采用非定常模拟方法。单继祥等[12-13]对对称折叠、顺向折叠方式下折叠翼的气动特性及展开运动过程进行数值模拟和动力学仿真,比较了折叠方式对折叠翼气动特性、展开运动特性的影响,并分析了影响机制。
2019年,Hui等[14]研究了受鸽子翅膀结构启发的仿生变形离散机翼,受变形骨架结构控制,机翼可主动变形为与鸽翼姿态相似的后掠翼构型,同时保持与鸽翼相似的离散翼面,结果表明,仿生机翼可在不同雷诺数下通过折叠变形保持最佳升阻比,并且可通过有效降低翼尖涡强度来实现无人机的诱导减阻,并提高无人机的横向稳定性。Cheung等[15-16]指出,通过允许在飞行过程中折叠翼尖,可以在一定程度上实现阵风载荷减缓,其基于折叠翼梢的概念设计了具有大幅降低弯曲刚度的大展弦比机翼,并将其置于带有垂直阵风发生器的低速风洞中,发现机翼根部的弯矩峰值减少了11%;此外,其在折叠翼梢上安装了一个可移动的二次空气动力表面,该装置能够在稳定的空气动力条件下有效地控制折叠翼梢的方向,并通过主动控制进一步降低阵风过程中的机翼根部峰值弯矩。宋慧心等[17]基于多刚体动力学对折叠翼飞行器建模,并对其变形进行稳定控制,通过气动计算拟合出气动参数与折叠角之间的函数关系,由此分析不同折叠角速度下飞行器的纵向动态特性,结果表明,折叠翼飞行器变形过程中速度、高度和扭转角均会发生变化。徐伟等[18]对处于极端工况和强气流环境下的折叠翼飞机进行模态和流固耦合分析,结果表明其所设计的折叠翼飞机能够满足极限工况环境下的强度和刚度要求。
2021年,Healy等[19]通过数值仿真和试验手段研究了外展折叠翼尖对飞机机翼滚转性能的影响,其设计、制造和测试了相应的滚动装置,并对不同长度翼展和折叠翼尖的机翼进行了测试,结果表明在飞机机翼上使用外展折叠翼尖可以提高空气动力性能,同时可显著减低由于滚转引起的空气动力阻尼。Favel等[20]提出一种具有几何非线性的飞机气动弹性建模方法,其构建了用于三维非线性结构动力学的模态模型,将机翼的线性段与非线性耦合项联系起来,模型的非线性是通过将机翼结构沿展向分成几个部分引入,在分段的界面处使用虚拟质量以有效减少分段数量并获得足够的计算精度。詹玖榆等[21]提出一种基于流形切空间插值的可折叠式变体机翼参数化气动弹性建模方法,并以一小展弦比折叠翼为研究对象,从折叠翼自由振动时的参变模态特性、颤振边界预测两方面进行了算例验证。初雨田等[22]基于离散化的思想对折叠翼进行建模,并利用Fluent软件对其进行数值计算,从升力系数和阻力系数变化及压力分布分析舰载机折叠翼的气动特性。Huang等[23]提出一种对具有双线性铰链刚度折叠翼的参数化建模方法,可在不同折叠角度下对机翼结构进行非线性参数化描述。Rafic[24]研究了外展铰链式的折叠翼尖对窄体运输机气动导数和飞行动力学的影响,并评估了折叠角和翼尖尺寸对机翼载荷的影响。
本文将基于弯扭组合梁元构建大展弦比等剖面多段折叠翼的结构动力学模型,并根据修正的片条理论得到有限翼展升力面的气动力,最后引入V-g法(V为机翼与未扰空气之间的相对速度,g为人工结构阻尼)得到多段折叠翼的颤振速度和颤振频率。
1 大展弦比等剖面多段折叠翼几何模型
考虑如图1所示的等剖面多段折叠翼,共分为n段,其中第k段的长度记为Lk,折叠角记为ηk,k=1,2,…,n。

图1 等剖面多段折叠翼Fig.1 A multi-segment folding wing with equal section

与舒展状态相比,机翼进行折叠后其整体刚性会发生较大改变,并且,结构几何形状的改变带来了气动力的重新分布,可以预料机翼的颤振特性将发生较大的改变。所以,有必要对等剖面多段折叠翼的颤振特性进行研究,以保证飞机结构的安全性。
2 基于弯扭组合梁元的结构动力学模型
2.1 局部坐标系中的弯扭组合梁元
基于有限元法对折叠翼的分段梁式结构模型进行离散,作用在梁单元上的载荷既包括面内横向气动升力,还包括气动力对弹性轴产生的气动力矩。这实际上是一个空间梁元问题,然而,在平面一般梁元的基础上再叠加扭转自由度也可模拟弯扭载荷共同作用下的梁式模型。在局部坐标系中,叠加了轴向位移和扭转角的平面直梁单元每个节点的自由度有4个,包括轴向位移v、横向挠度w和面内转角θ和扭转角α,如图2所示。

图2 局部坐标系中的弯扭直梁单元Fig.2 A beam element considering bending and torsion deformations in a local coordinate system

(1)
在局部坐标系中,弯扭组合梁元的势能为
(2)
对于梁元的弯曲变形,选取2节点Hermite单元,其弯曲位移模式为
w=Nw·we=[Nw1,Nw2,Nw3,Nw4]·[wi,θi,wj,θj]T
(3)
式中:Nw1=1-3ξ2+2ξ3,Nw2=(ξ-2ξ2+ξ3)l,Nw3=3ξ2-2ξ3,Nw4=(ξ3-ξ2)l,ξ=yi/l为单元内的自然坐标,且有0≤ξ≤1。而对于梁元的轴向变形和扭转变形,选取基于1维Lagrange插值多项式表示的位移模式,分别为
v=Nvve,α=Nααe
(4)
式中:Nv=Nα=[N1,N2]=[1-ξ,ξ];ve=[vi,vj]T;αe=[αi,αj]T。
将(3)式和(4)式代入(2)式,弯扭梁元的势能可重写为
(5)
(6)
另外,图1(b)所示机翼截面中任意一点的速度为
(7)
忽略弯扭梁元轴线方向的变形速度,其动能为
(8)
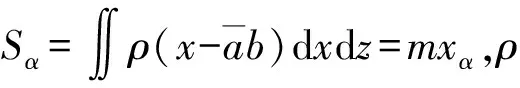
(9)
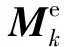
(10)
第k段机翼上非定常气动力所做的虚功为

(11)
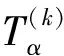

(12)

(13)
(14)
(15)
由(6)式、(10)式和(12)式,忽略结构阻尼,可得第k段机翼上局部坐标系中弯扭梁元的有限元方程
(16)
2.2 模态坐标系下的多段折叠翼动力学方程

(17)
式中:
(18)
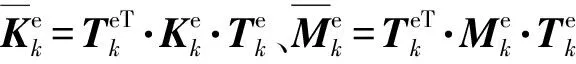

(19)

对机翼根部施加约束,并进行模态分析得到振型矩阵Φ。采用模态截断法,仅引入较低的前r阶固有频率和振型参与气动弹性计算,记截断后的振型矩阵为
Φ*=[φ(1)φ(2)…φ(r)]
(20)
主坐标列阵为
(21)
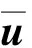
(22)
在(19)式两端同时乘以Φ*T,可得到模态坐标系下的多段折叠翼整体结构动力学方程:
(23)
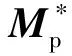
3 颤振计算
对于等剖面大展弦比机翼,在空气动力学方面近似采用片条理论或修正的片条理论可得到有限翼展升力面的气动力。所以,可将机翼沿展向划分为若干气动片条,将作用在每一个片条上的气动力视为二维气动力。在进行气动弹性分析时,需要在结构和空气动力之间提供相互连接的途径,通常是将结构响应数据和空气动力数据通过样条插值实现相互传递。为方便起见,不失一般性地,可将空气动力片条划分规则与机翼结构弯扭梁元划分规则取为一致。如此,作用在每一个弯扭梁元上的气动载荷可视为是均匀分布的,可通过(12)式将气动升力和气动扭矩分配到弯扭梁元上的节点上。假设机翼和空气的相对速度为V,空气密度为ρa,根据Theodorsen非定常气动力理论,单位展长机翼所受的气动力为
(24)
(25)
式中:h为机翼的沉浮位移,向下为正;α为机翼攻角,抬头为正;C(kR)为Theodorsen函数(以下简记为C);变元kR=ωb/V为折合频率,ω为机翼作简谐运动的角频率。
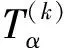
(26)
(27)
根据(3)式和(4)式,(26)式和(27)式中的wk和αk分别为
wk=Nw(1/2)·we,αk=Nα(1/2)·αe
(28)
从而(15)式可重写为矩阵形式:
(29)
式中:
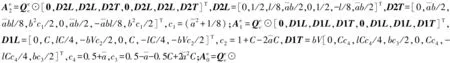
将(29)式代入(16)式,可得第k段机翼在局部坐标系中的有限元方程为
(30)

(31)
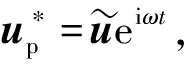
(32)
式中:
(33)
由颤振方程得到特征值为
(34)
进一步得到
(35)
4 数值算例
考察一个等剖面三段式折叠机翼,完全舒展状态时为一大展弦比机翼[25],如图3所示,其物理参数如表1所示,进行颤振计算时取空气密度为1.225 kg/m3。取前2阶弯曲模态(固有频率分别为3.069 28 Hz、19.236 2 Hz)和前2阶扭转模态(固有频率分别为45.782 7 Hz、137.348 Hz)参与计算,将该等剖面大展弦比机翼的颤振计算结果如图4所示。
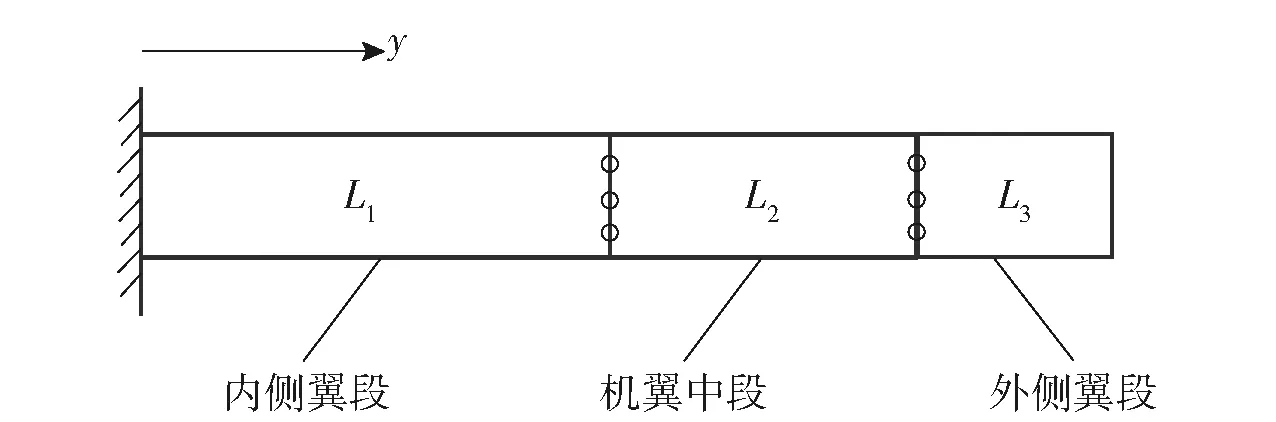
图3 等剖面三段式折叠机翼Fig.3 A three-segment folding wing with equal section
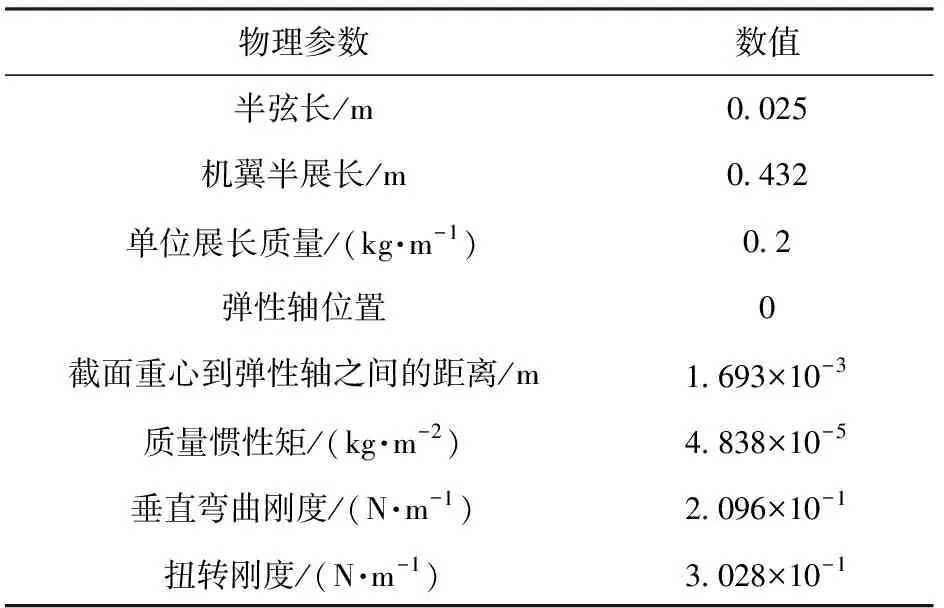
表1 大展弦比机翼的物理参数
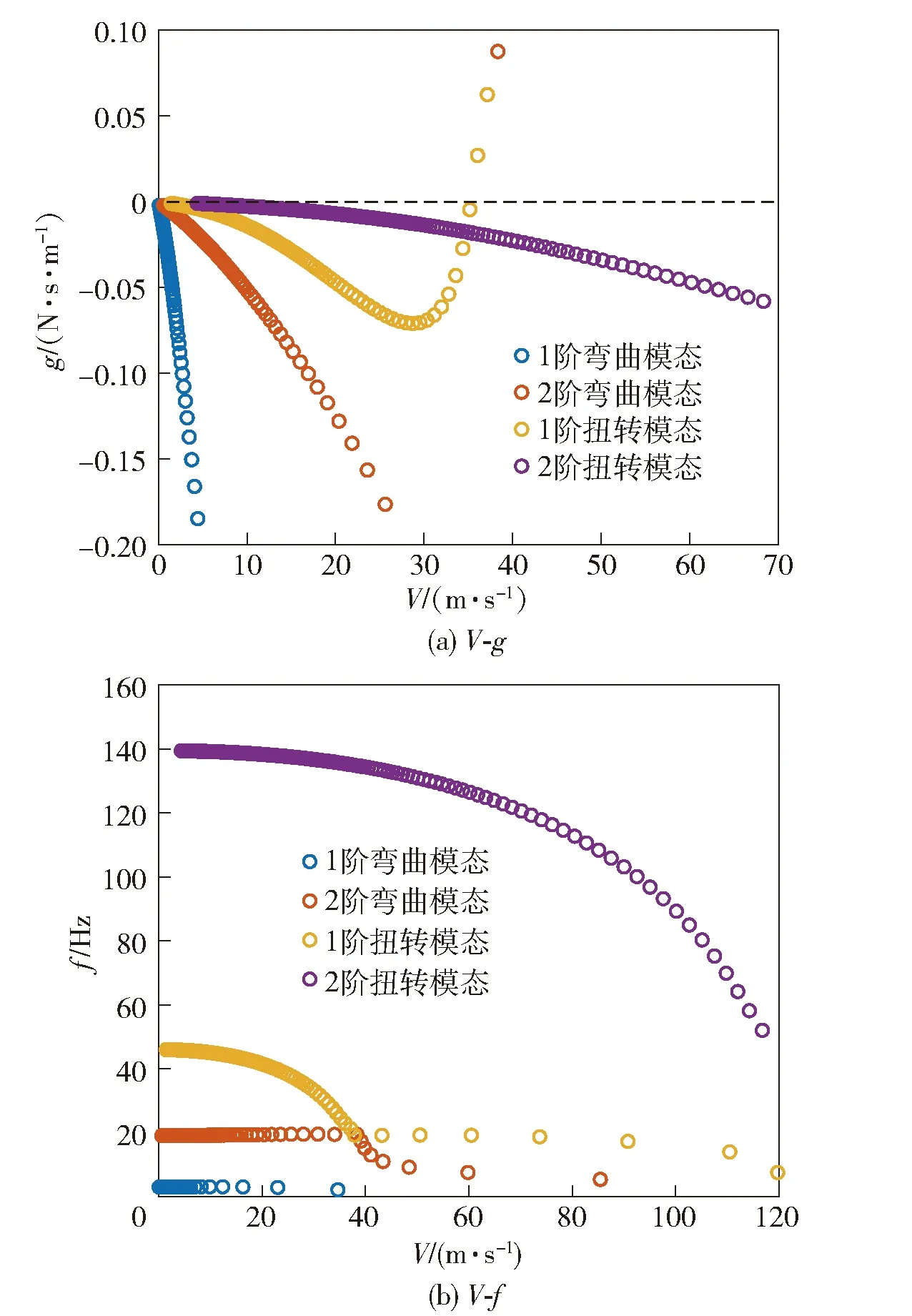
图4 颤振计算结果Fig.4 Results of flutter analysis
由图4可知,该机翼颤振现象出现在第1阶扭转模态上,颤振速度VF0=35.22 m/s,颤振频率fF0=24.29 Hz。赵永辉等[25]使用与本文同样的物理参数,并取前两阶弯曲模态和前两阶扭转模态参与计算,得到的颤振速度为35.3 m/s,颤振频率为24 Hz。与其相比,使用本文方法计算得到的颤振速度误差为0.23%,颤振频率误差为1.21%。
4.1 多段折叠翼固有频率特征
机翼折叠后,结构固有频率可能发生大的变化,在原有的颤振速度下机翼从气流中获取的能量将不能维持其简谐振动的要求,所以折叠后机翼的固有频率会对颤振速度有重要影响。另一方面,机翼在折叠后,折叠部分机翼的升力将随着折叠角的增大而减小,当折叠角增至90°时,折叠部分机翼不再产生升力。而当折叠角进一步增大时,其气动特性将是复杂的,并可能会引起升力面的反效。所以,为保证翼面的可操纵性,在本文的工作中,对各段机翼折叠角的范围进行限制,即令ηk∈[0°,90°),这意味着各段机翼只能向上折叠且折叠角要小于90°。
约束机翼根部,由模态坐标系下的多段折叠翼整体结构动力学方程(23)式可知,机翼的固有频率为
(36)
以三段式折叠翼为例,约束机翼折叠角向量为η=[0,η2,η3],翼段长度向量为L=L/3×[1,1,1]T时,三段式折叠翼的前3阶固有频率随折叠角的变化如图5所示。
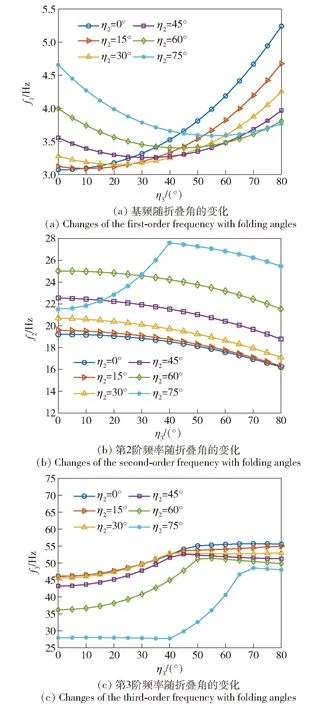
图5 机翼结构前3阶频率随折叠角的变化Fig.5 Changes of the first three order frequencies of the wing structure with folding angles
图5中,折叠角η2由0°角开始,每隔15°均匀变化至75°,而折叠角η3则由0°角间隔10°均匀变化至80°。由图5(a)可知,机翼的1阶固有频率f1随着折叠角η2和η3的变化呈现出非线性变化的趋势。当η2较小时(小于30°),f1随着η3的增大而单调递增,且η2值越小,f1的增长速度越快,至η3为80°时,f1达到5.240 5 Hz,相比舒展状态机翼增长了70.74%。而当η2较大时(大于45°),η2越大则f1也越大,且f1随着折叠角η3的增大会呈现先减小而后再增大的趋势。有意思的是,机翼1阶固有频率曲线簇在η3为45°附近表现为“谷”。具体地,当两段机翼的折叠角均为45°时,f1的值为3.301 8 Hz,仅比舒展状态机翼增长7.58%,即单段机翼大的折叠角对其1阶固有频率的影响更为显著。由图5(b)可知,当η2不大于60°时,机翼2阶固有频率f2随η3的增长呈递减趋势,且η2越大f2也越大。然而,这一现象在η2达到75°时发生了根本性的变化,在η3为0°时,f2的值低于η2为45°时的值,之后随着η3的增长而快速变化,至40°时达到27.608 7 Hz。而随着η3的进一步增大,f2开始减小,其规律与其他折叠角情形相同。由图5(c)可知,当η3为0°时,f3随着η2的增大而减小,这一现象在η2小于30°时并不明显,但当η2超过45°时,f3开始急剧降低。随着η3的增大,f3曲线簇开始聚集并集中在50 Hz附近。
由图5可知,机翼结构的前3阶固有频率均在一定程度上呈现出非线性的增长规律,这是由于弯扭组合梁元在发生折叠时,单元刚度矩阵和单元质量矩阵需要经过坐标变换才能组装进整体刚度矩阵和整体质量矩阵。而坐标变换矩阵里面包含了折叠角的正弦或余弦值,若将坐标变换矩阵看作关于折叠角的函数矩阵,则该函数矩阵为一簇随折叠角非线性变化的曲线。另一方面,图5中折叠后机翼的固有频率相比未折叠状态具有一定程度地提高,这是由于大展弦比机翼总是呈现出较“柔”的特征,将机翼折叠后,大展弦比机翼在长度方向变短,提高了机翼结构的整体刚性。
4.2 折叠翼颤振计算
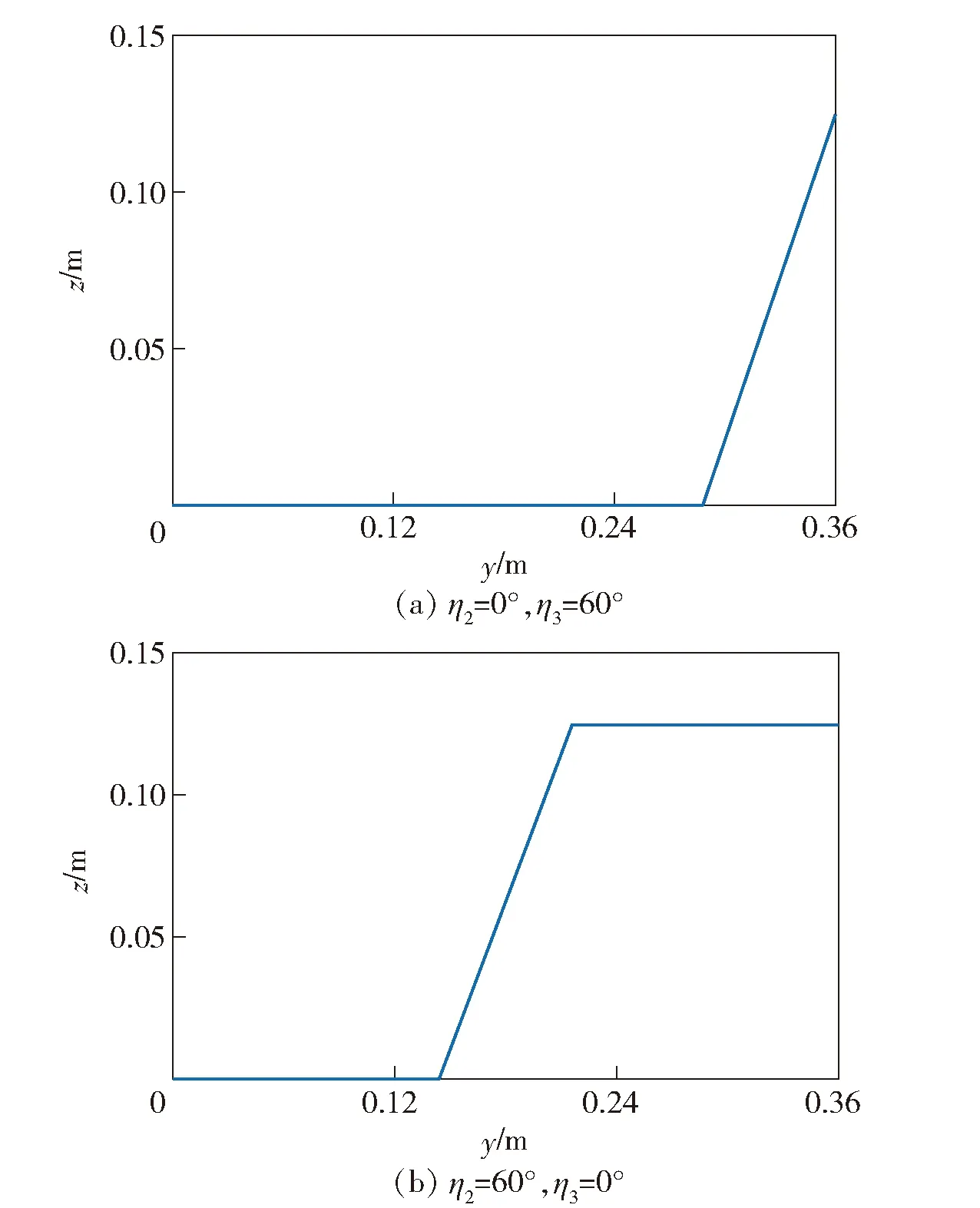
图6 两种不同折叠方式的机翼Fig.6 Wings with two different folding modes
考虑两种不同折叠方式的机翼,如图6所示。两种情况下机翼的折叠角向量分别为[0°,0°,60°]和[0°,60°,0°],第1种情况主要反映了翼尖折叠对机翼颤振带来的影响,而第2种情况则主要考察折叠角沿y轴向后移给机翼颤振速度和颤振频率带来的影响。为此,将第1种折叠方式下的V-g图和V-f图如图7所示,而将第2种折叠方式下的V-g图和V-f图如图8所示。

图7 第1种折叠方式下的V-g和V-f图Fig.7 Diagrams of V-g and V-f under the first folding mode
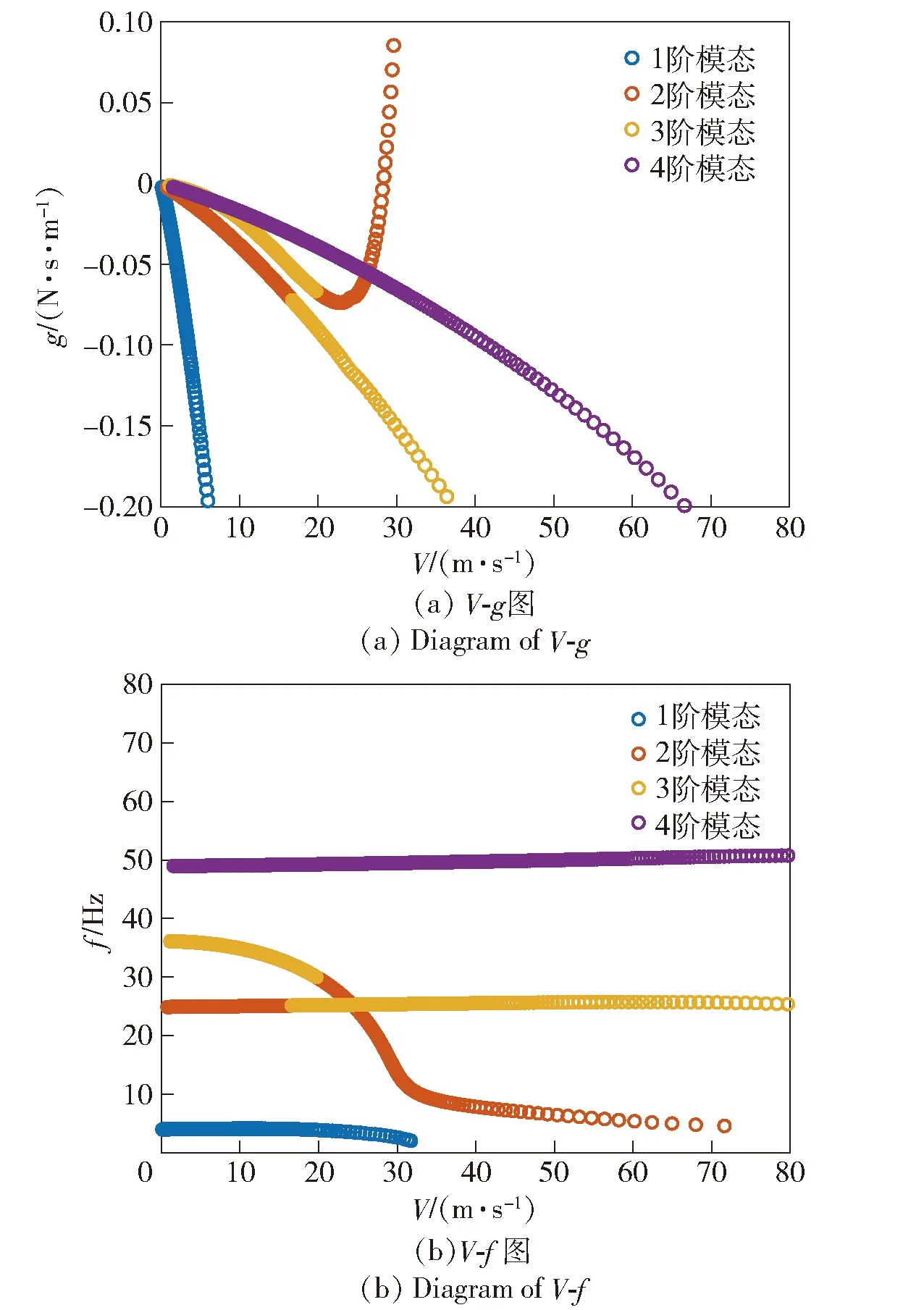
图8 第2种折叠方式下的V-g和V-f图Fig.8 Diagrams of V-g and V-f under the second folding mode
由图7(a)可知,折叠角向量为[0°,0°,60°]的机翼颤振速度为46.43 m/s,较未折叠前机翼的颤振速度35.22 m/s 提高了11.21 m/s,提高比例达到了31.83%。同时,由图7(b)可知,在该颤振速度下,机翼对应的颤振频率为30.95 Hz,同样较未折叠前机翼的颤振频率24.29 Hz提高了6.66 Hz,提高比例为27.42%。由此可见,折叠翼尖对机翼颤振速度和颤振频率的提高具有积极意义。
然而,当机翼折叠角向量为[0°,60°,0°]时,机翼的颤振模态从第3阶的扭转模态迁移至第2阶弯曲模态,致使颤振速度和颤振频率都发生了相应地下降,分别为28.28 m/s和17.92 Hz。即当将机翼中部进行折叠而保持翼尖平直时,机翼易发生颤振模态跳转而使得颤振速度和颤振频率下降。
为更深入地考察折叠角η2和η3对机翼颤振速度VF和颤振频率fF的影响性规律,令机翼翼尖折叠角η3从0°均匀变化至80°,而η2从0°间隔15°绘制颤振速度和颤振频率的变化曲线,如图9所示。
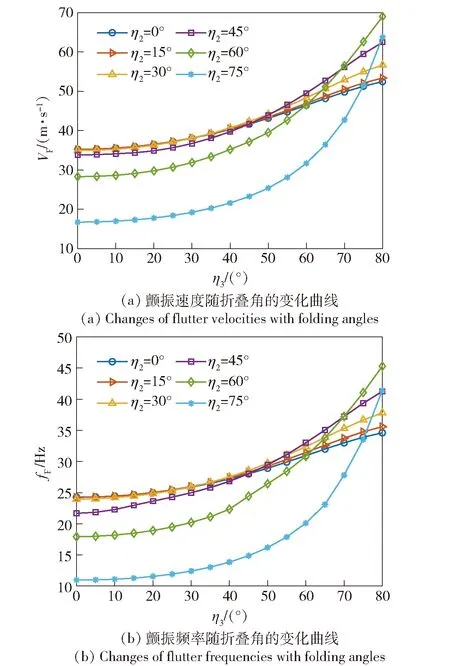
图9 颤振速度和颤振频率随折叠角的变化曲线Fig.9 Changes of flutter velocities and frequencies with folding angles
由图9可知,颤振速度和颤振频率随折叠角η2和η3的变化规律基本相同。当折叠角η3较小时,折叠角η2越大,机翼颤振速度和颤振频率越小,并且这种递减的趋势是非均匀的。当η2不大于30°时,颤振速度和颤振频率对η2的变化不敏感,而当η2大于45°时,颤振速度和颤振频率随η2的下降速度不断增大。
另一方面,随着翼尖折叠角η3的增大,机翼颤阵速度和颤振频率均呈现递增趋势。而η2越大,机翼颤阵速度和颤振频率的增速越大。当η2和η3均较大时,机翼颤振速度和颤振频率也具有较大的数值。这相当于是将折叠翼尖带来的增益效果向机翼中段进行了扩展。
4.3 折叠段数对颤振速度的影响
本节在各段机翼均匀折叠的情况下考察折叠段数对颤振速度的影响性规律。记第n段机翼的折叠角为ηn,则第k段机翼的折叠角为
(37)
当ηn分别为80°、60°和40°时,将机翼的颤振速度和颤振频率随机翼段数n的变化如图10所示。
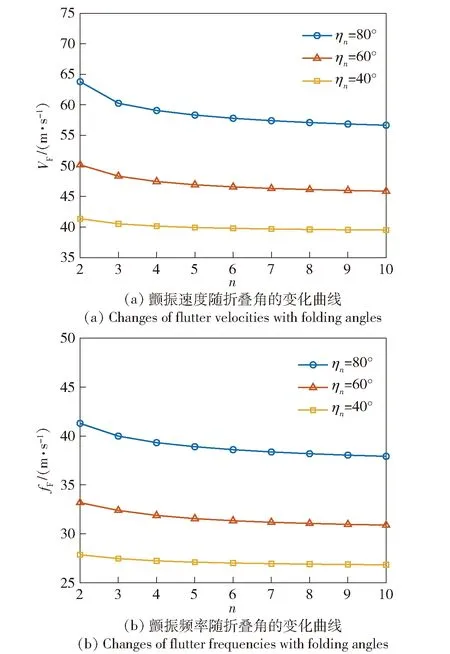
图10 颤振速度和颤振频率随折叠段数的变化曲线Fig.10 Changes of flutter velocities and frequencies with the number of folding segments
由图10(a)可以看出,机翼颤振速度随着机翼段数n的增大而减小。当翼梢处折叠角为80°时,颤振速度从n=2时的63.8 m/s减小至n=10的56.7 m/s。并且,曲线斜率在n为2或3时较大,在大于3后曲线斜率变化较小。也就是说,在机翼段数大于3时,机翼段数对颤振速度的影响并不明显。另一方面,随着最大折叠角ηn的减小,机翼颤振速度明显下降。在ηn为60°时,2段机翼的颤振速度下降为50.17 m/s,而在ηn为40°时,则下降为41.36 m/s。由图10(b)可知,机翼颤振频率随折叠段数的变化规律与颤振速度的变化规律基本相同。
由此可见,当翼尖最大折叠角固定时,机翼的颤振速度随折叠段数的增加而减小,但减小的幅度并不明显。当仅有两段机翼时,虽然可获得较高的颤振速度,但两段之间过大的折叠角可能会引起气动方面的问题,同时在结构设计方面也会面临更大的困难(例如折叠开缝问题)。而多段折叠机翼的颤振速度下降并不明显,但可降低对折叠翼气动和结构设计方面的要求。
5 结论
1)基于弯扭组合梁元构建的大展弦比等剖面多段折叠翼结构动力学模型能够合理描述机翼弯曲和扭转两种变形形态,而根据修正片条理论得到的各梁段机翼上的频域非定常气动力被离散为气动影响系数矩阵添加至颤振方程。
2)多段折叠翼的固有频率随折叠角的变化而发生改变,这种改变呈现出非线性形态。机翼的1阶固有频率曲线簇在外侧机翼折叠角为45°附近表现为“谷”,且单段机翼较大的折叠角对其1阶固有频率的影响更为显著。另外,第3阶固有频率的曲线簇聚集在50 Hz附近。
3)折叠翼尖对机翼颤振速度和颤振频率的提高具有积极意义。当机翼折叠角变化时,颤振模态可能会发生跳转和迁移,致使颤振速度和颤振频率都发生相应地下降。另外,颤振速度和颤振频率随折叠角变化规律基本相同。
4)当翼尖最大折叠角固定时,机翼的颤振速度随折叠段数的增加而减小,但减小的幅度并不明显,这一现象可明显降低对折叠翼在气动和结构设计上的要求。

