矢量喷水推进两栖车航行姿态的数值及试验分析
王野, 陈慧岩, 汪泰霖, 张富毅, 王典, 司璐璐
(1.北京理工大学 机械与车辆学院, 北京 100081; 2.上海船用柴油机研究所, 上海 200090)
0 引言
水陆两栖车是一种既可以在水上航行也可以在陆上行驶的交通运输工具[1]。两栖车的陆上行驶特性与陆地车辆较为相似,水上动态性能主要体现在三个方面:快速性、耐波形和操纵性[2]。其中快速性主要为最高航速、水上加速性等水上航行特性;耐波性体现了两栖车辆的抗风浪能力;操纵性是指两栖车辆根据驾驶员的意图改变或保持其运动状态即航速、航向和位置的性能。随着各国争相发展高速两栖车技术,两栖车已经广泛应用于交通运输、抢险救灾、测绘勘探、海洋地质学和气象学等领域[3-4],提高两栖车快速性的同时也因作业场景需求对两栖车的耐波性和操纵性提出了较高的要求[5]。
对于两栖车而言,由动力结构决定的欠驱动性、航行环境导致的强非线性和扰动不确定性,因而两栖车在受到风浪洋流等环境扰动时会不可避免地出现偏航和摇摆现象[6],尤其在高速航行时,对两栖车的航行稳定性产生了较大影响。为解决欠驱动和易受扰动这一问题,可控推进力矢量化就成了研究的重点。
矢量推进技术最早应用于航空发动机,通过控制发动机尾喷气流的方向获得矢量驱动力,主要有摆动喷管式、超声速分离线喷管、二次喷射(辅助流体喷射)等方式[7-8]。类比于空天领域中的矢量发动机技术,在水域航行领域已经有相当一部分研究考虑矢量推进技术在水面船舶、潜航器及水下机器人上的应用。
目前应用于水域航行器的推力矢量化技术一般通过两种工作方式实现:一种是布置多对具有不同推进朝向的推进器,通过不同朝向的推进器组合,获得不同主方向的推力效果;另一种是直接采用单个推进器,推进器的朝向可以通过控制附加机构来进行调整[9]。
考虑多推进器策略的研究有:Lin等[10-11]使用的三喷水推进器推进系统,分别用于应对球形航行器纵荡、垂荡、横摇等运动。张帅等[12]提出的船体两侧布置螺旋推进舵的主动式船舶减摇装置。郑昆山[13]设计的水下矢量推进装置,通过设置在潜行器末端的二元可控矢量喷头实现潜行器的运动控制,但也导致潜行器无法直接实现侧向移动。
上述这类多推进器构型设计的不足主要是结构设计冗余,多推进器质量较大,外流场形状阻力更大,同时副推进器的间歇工作导致多推进器结构综合利用效率并不高,因此一些学者提出通过使用单推进器附加二次调节结构的方法实现推力矢量的调整。
早在2004年,Cavallo等[14]研制了一种3自由度旋转螺旋桨矢量推进器,稳定尾翼的同时定向推进航行器。王聘[15]提出一种采用机械导流板来偏转推进器尾流推力的矢量控制技术。武建国等[16]在2018年设计了十字形矢量舵,通过推进器的差动控制实现航向改变。魏东杰[17]提出一种采用3-RPS与球形万向节的组合传动机构并联式矢量推进器。Ba等[18]利用矢量喷口定向控制容积泵产生的水射流,从而实现航行器在水下空间的大角度偏转。基于这些附加机构的推力矢量技术虽然没有在数目上增加推进器的数量,但是整体航行器的传动设计需要考虑附加机构的驱动,使得系统的复杂性增加,且这部分的机械传动会消耗一部分能量,同样导致形状阻力的增加,航行器整体推进效率降低。
虽然矢量推进技术广泛应用于水面舰艇和水下航行器上,但是在两栖车辆上的应用较少。多推进器的矢量驱动因空间布置限制和能耗效率等问题难以在两栖车上实现,而加装外附件的方式也因为易剐蹭、影响出入水等原因不适宜安装在两栖车上。相较于采用多推进器构型和附加机构的矢量推进器,本文在单推进器的结构基础上引入可控的矢量喷口,采用车体、水泵、推进器一体化设计,避免了冗余的附加结构。通过与内流道嵌合的2自由度矢量喷口,获得方向可控的矢量推进力,实现航向保持和纵摇姿态调整的功能。该矢量喷水推进器具有重量轻、体积小、成本低等优点。针对两栖车的欠驱动和强非线性的特点,在保证一定快速性的前提下,使两栖车获得更好的耐波性和操纵性。
本文首先介绍了矢量喷水推进器设计,并给出了矢量喷水推进器和两栖车的数值计算方法,然后分别用自航减摇试验和航向保持试验研究矢量喷水推进装置的实车效果,最后对仿真结果和试验结果进行了分析对比。
1 矢量喷水推进器及两栖车设计
1.1 矢量喷口
针对两栖车减摇和转向的功能需求,矢量喷水推进器需要产生可以抑制两栖车纵摇幅度的俯仰力矩以及供两栖车转向的横摆力矩。矢量喷水推进器由矢量喷口和喷水推进泵两部分组成。喷水推进泵提供矢量喷水推进器的输出推力,矢量喷口根据功能需求改变输出推力的方向。针对设计功能需求,喷口装置具有俯仰与旋转2个自由度,可以改变尾喷水射流角度以获得不同方向的矢量推进,输出三维矢量推力[19]。

图1 矢量喷口Fig.1 Vectoring nozzle
矢量喷水推进器基于喷口的动作,使用小齿轮副架设于旋转齿轮上达到俯仰和旋转动作两个圆弧运动的复合,从而获得机械限制内的全空间矢量方向。设计喷口如图1所示。喷口通过设计焊接固连的俯仰轴和轴套保证跟随强度;两对啮合的齿轮由伺服电机(内置霍尔传感器反馈角度值)驱动,实现精确位置控制;旋转电机跟随齿轮座圈通过套装在流道外侧的电旋转连接器实现无限制的连续旋转,电接触滑动连接利用环道和电刷的相对滑动解决了旋转电机的动力供应和信号传输问题;设于推进器电旋转连接器上方的旋转电机控制推进器矢量喷口绕矢量喷口中心轴旋转(0°≤β≤360°),设于推进器连接盘上方的俯仰电机控制矢量喷口在竖直方向上做俯仰运动(-30°≤α≤30°),α与β分别为喷口动作的俯仰角度与旋转角度。2个旋转自由度的运动组合成全矢量的喷口运动,完成各个方向的水射流,获得所需要的矢量推进力,实现方式示意图[19]如图2所示。

图2 矢量喷口动作示意图 Fig.2 Movements of the vectoring nozzle
矢量喷水推进器结构复杂,实际工作时因安装在车内,外部机械结构对推进器内部流动的影响较小,本文取矢量喷水推进器内部流道对矢量喷水推进器进行数值计算,相关参数如表1所示。

表1 矢量喷水推进器外形参数Table 1 Profile parameters of the vector water jet thruster
1.2 喷水推进泵
喷水推进泵是矢量喷水推进系统主要的动力输出部件,推进泵将主电机产生的轴功率通过叶轮转化为推进系统的推力输出。由于矢量喷水推进系统要求输出流量大,但扬程要求不高,故喷水推进泵采用设计结构简单,质量轻的轴流泵。表2给出了喷水推进泵主要水力参数。

表2 喷水推进泵主要水力参数Table 2 Main hydraulic parameters of the pump
1.3 两栖车
为了验证矢量喷水推进器的功能,本文采用了ITTC[20]推荐的满足傅汝德数相似换算的缩比模型试验方法[21],也是目前公认的测试方法和标准,主要参数如表3所示。定义随体坐标系Oxyz,沿车长方向向前为x轴正方向,沿车宽方向向右为y轴正方向,沿车高方向向下为z轴正方向,车辆随体坐标系如图3所示。

表3 两栖车主要参数Table 3 Main parameters of the amphibious vehicle
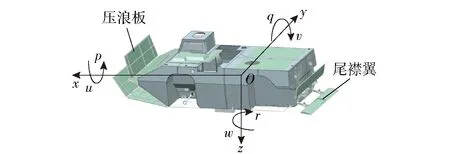
图3 随体坐标系Oxyz定义Fig.3 Definition of the body-fixed coordinate Oxyz
2 CFD数值计算
2.1 两栖车运动模型
两栖车可近似视为高弗汝德数的平底船,采用经典6自由度模型[22]:

(1)
η=[x,y,z,φ,θ,ψ]T
(2)
v=[u,v,w,p,q,r]T
(3)
式中:M是惯性矩阵;C是科里奥利力和向心力矩阵;v是速度和角速度,v的方向定义由图3给出;D是阻尼矩阵;η为位移和角位移;g(η)表示广义重力和浮力及其产生的力矩;g0是由压载水系统和水箱产生的恢复力和恢复力矩;τwave是由波浪引起的压力变化而产生波浪激励力;τwind是风荷激励力;τ是广义外力和外力矩。
在考虑两栖车的纵倾稳定性控制时,假定两栖车的航向不变,且不发生横荡横摇,仅考虑纵荡,垂荡,纵摇运动, 简化为3自由度纵向模型,如(4)式所示。考虑两栖车的转向控制时,假定两栖车仅在水平面内运动,即两栖车不发生垂荡、纵摇、横摇,仅考虑纵荡、横荡、艏摇运动,简化为3自由度水平面模型,如(5)式所示。
(4)
(5)
式中:m表示车体质量;xg、yg、zg表示车辆重心在随体坐标系中的坐标;X、Y、Z、K和N表示外力和力矩,包括风浪洋流对车体的作用,矢量喷水推进器产生的推进力、力矩以及水动力和水静力;In(n=yb,zb)表示车体对随体坐标系Oxyz的y轴和z轴惯性矩。
矢量喷水推进器的输出总推力T可按旋转角和俯仰角作如下分解[19]:
(6)
式中:Tx、Ty、Tz分别为总推力T在x轴、y轴、z轴的分力。
输出推力作用点到车体重心的位置矢量定义为
(7)
式中:xT、yT、zT为车体重心在随体坐标系中的坐标。则喷口输出推力矩为
(8)
式中:KT、MT、NT为喷口输出推力对车体在随体坐标系三个轴向上的力矩。
两栖车处于平衡状态时,外力和外力矩均为0,当两栖车遭遇纵波时,τwave发生变化,为了消除τwave变化产生的影响,喷口转至俯仰角α处。因喷口流量不变,忽略喷口总推力的变化。假设两栖车遭遇波浪产生的纵倾角为θ,Of设为两栖车漂心也即其重心,正浮状态下的浮心位置为c0,纵倾θ角后浮心位置为c1,则
(9)
式中:V是排水体积;Iθ是两栖车设计水线面面积对纵倾轴(过漂心O的横轴线)的惯性积。
设车体浮力为FB,则由浮心位移产生的恢复力矩Mθ为
(10)
则关于两栖车纵摇和艏摇状态的平衡方程可以分别表示为
(11)
(12)

2.2 CFD模型
采用不可压缩流体的运动方程求解流场信息,表达式[23]为
(13)
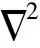
考虑到矢量喷水推进器的复杂管内流动,使用SSTk-ω模型进行计算,湍动能k和湍流频率ω方程[24]分别为
(14)
(15)
式中:t为时间;xi、xj和xk为位置坐标;ui、uj和uk为速度分量;μt为湍流黏性系数;F1为第一混合函数;Pk为湍动能生成项,
(16)
其中模型常数取值:β′=0.09,α=5/9,β=0.075,σk=1.00,σω1=0.5,σω2=0.856。
两栖车辆在水面航行时,会对自由液面产生扰动。目前主流的模拟方法为使用体积流量(VOF)法[25]实现自由液面的捕捉。本文研究的流体介质为水和空气,目标流体相为空气。假设空气相所在的域为V1,水相所在的域设为V2,流体所在项为x,可得
(17)
对于两种不相容的流体组成的流场,α(x,t)满足:
(18)
式中:V=(u,v,w)为流体的速度场。定义VOF函数Cijk为α(x,t)在网格单元上的积分除以单元体积ΔVijk:
(19)
并且Cijk满足:
(20)
当Cijk=1时,网格充满空气相;当Cijk=0时,网格不含空气相;当0 由于矢量喷水推进器的性能与车体结构和两栖车航况密切相关,因此在对矢量喷水推进器进行数值模拟时应考虑喷口尾部和两栖车周围的流场区域。根据文献[26],计算域被确定为30D×10D×8D的正交区域内,计算域及边界条件设置如图4所示。 将整个计算域分为喷口段、叶轮区域、导叶区域和进水流道段4个部分进行单独划分。各个部分近壁区域按表4计算布置边界层网格, 采用基于多参考系的动参考系(MRF)方法处理旋转区域。进水流道段与叶轮区域、叶轮区域与导叶区域之间通过动静交接面连通,导叶区域与矢量喷口段通过静- 静交接面连通。 图4 计算域及边界条件Fig.4 Calculation domain and boundary conditions 表4 边界层参数 结合使用TurboGrid软件和ICEM软件对叶轮区域和导叶区域进行网格划分,在TurboGrid中进行单流道网格划分,再利用ICEM对单流道网格周期阵列并删除重复节点,从而得到全流道网格[27]。喷口段旋转流域的流动较为复杂,分为两个小区域,喷口运动区域网格为旋转网格,其他区域为静止网格,如图5所示。进水流道以及车底水域均采用自适应加密的非结构化网格,在进水流道以及进水口附近的车底区域进行局部网格加密,在流道和泵轴近壁区采用边界层网格[28]。 图5 喷口段网格Fig.5 Nozzle segment meshes 本文采用ANSYS CFX软件进行数值模拟。湍流模型使用SSTk-ω模型,控制方程和湍流模型采用二阶迎风格式离散。监测计算中各物理量的残差收敛情况,收敛标准为小于10-4。 为了获得实时反馈的喷口控制对两栖车姿态调整的动态模拟效果,本文基于CFX计算形成的推力数据库,联合Vortex建立矢量推进两栖车的水上航行模拟仿真平台。 根据图3所示的两栖车几何模型,通过Vortex仿真系统的part单元建立与车体形状相同的物理计算实体,对矢量喷口部分进行单独建模,增加运动约束到两栖车上,并与CFD计算得到的喷口输出推力进行关联。分别设置各个实体单元的阻力、浮力、动升力以及碰撞检测,如图6[29]所示。 图6 两栖车实体分化示意图Fig.6 Structure of the amphibious vehicle 各单元浮力FB、阻力FR与动升力FL分别为 FB=-ρbVg (21) (22) (23) 式中:b是根据排水量计算的浮力系数;d是阻力系数;l是升力系数;vu是计算单元相对于流体的速度;A计算单元是垂直于相对速度的横截面积;n是表面法线。 两栖车仿真实验环境设定为一片开阔水域,本文采用二维海面法对海面进行描述,通过点阵将空间分割为海洋与大气两部分。对仿真实体单元中z轴坐标低于水面二维点阵的部分进行浮力、动升力等作用力的求解。 为了模拟两栖车航行时矢量喷水推进器动作对两栖车航行状态的实时影响,本文使用前述CFD计算方法计算在不同航速,各个俯仰角、旋转角工况下的矢量喷水推进器的输出矢量推力,在对转角进行拟合后,再根据傅汝德数缩比关系对推进泵转速(对应推阻力平衡航速)拟合,得到喷水推进器推力随行驶速度和俯仰角度变化函数曲线插入Vortex仿真系统中,形成的推力数据库作为喷口不同状态下即时反馈的输出推力。 仿真过程中可以通过矢量喷水推进器对车辆行驶状态进行控制,推力输出模块按照矢量喷水推进器即时状态参数进行推力数据调用,实时反馈航行状态的数据以及控制响应情况。 矢量两栖车试验包括矢量喷水推进器的台架试验、强制自航减摇试验、自由自航航向保持试验三个部分,分别验证推进器的输出能力、矢量喷水推进器对两栖车的减摇效果、矢量喷水推进两栖车的转向性能。 试验在大连理工大学船舶工程学院船模拖曳水池上进行,水池尺度为160 m×7 m×3.7 m(长×宽×水深),水池拖车速度范围为:0.01~8 m/s,速度精度为0.1%。水池造波机为机电摇板式,所造波浪为规则波。波长范围λ为2~12 m。波浪参数由KGY- 1型可控硅浪高仪测得。浪高仪置于水池右侧距池壁1.5 m,距造波板50 m处。本次试验数据的记录与处理由DHDAS动态信号采集分析系统完成。 矢量喷口台架试验时将矢量喷水推进器及各设备装车后,测得整车质量为222.1 kg。将矢量两栖车固定于试验台架上,连接扭矩仪及三轴测力仪。 试验中,针对不同航速下推阻力平衡的喷水推进泵转速(944 r/min、1 190 r/min、1 904 r/min)分别改变矢量喷口旋转角度β(0°、45°、90°)及俯仰角度α(30°、20°、10°、0°、-10°、-20°、-30°)共57组工况,工况设置如图7所示。其中,两栖车左右关于中心线轴对称,故旋转角度只需考虑二分之一圆周试验。在每个工况下,利用三轴测力仪记录的电压值,由DHDAS系统给出矢量喷水推进器的三轴输出推力。 图7 台架试验57个工况Fig.7 57 conditions of the bench test 两栖车通过导向杆与拖车相连,因为纵摇试验只验证两栖车的纵摇响应,导向杆限制了两栖车的侧向位移(横荡)。拖车在滑轨上行驶,与自航的两栖车保持纵向的相对静止,强制力由导向杆补足。通过安装在两栖车头部的姿态传感器反馈的电压值,测算得到两栖车的姿态变化,如图8所示。 图8 强制自航减摇试验Fig.8 Forced-running experiment for stabilization verification 试验时,由造波机制造波长12 m,浪高50 cm的规则波,在矢量喷口直喷的工况下,由拖车牵引两栖车在恒定航速即喷泵转速固定的条件下航行,记录两栖车遭遇波浪时车体纵倾角的变化;待水面状态平静后,重复造波,牵引两栖车迎浪航行,针对惯导反馈的两栖车纵倾角变化,手动通过遥控驾驶仪界面控制喷口的俯仰动作,记录两栖车遭遇波浪时车体纵倾角的变化。两组试验结果进行对照,验证矢量喷水推进器功能。 自由自航试验用以验证装配有矢量喷水推进器的两栖车的航向保持能力。自由自航试验中,对两栖车不施加约束,使其可以自由航行,模拟实际航行的工况。 试验时,初始状态保持矢量喷口俯仰角α与旋转角β为0°,开动两栖车,当外界水流波浪影响致使两栖车的姿态发生变化时,试验员根据惯导反馈的车体航向角信息,通过上位机驾驶仪控制喷口的旋转动作,从而使两栖车恢复原始航向,控制两栖车的横向位移在一个较小的范围内,两栖车航行实拍图如图9所示。记录惯导反馈的两栖车位置和航向角信息。 图9 自由自航航向保持试验Fig.9 Free-running experiment for heading-keeping verification 5.1.1 CFD网格可信度分析 在对矢量喷水推进器输出推力的CFD计算中,需要对仿真结果进行可信度评估。根据关于安全系数的Richardson 外推法,本文建立了4套粗细程度不同的网格用于计算离散化误差。本仿真实际为得到对应工况下推进器的输出推力,故以无量纲数输出总推力系数CT作为评价网格可信度的指标量。本仿真喷口输出总推力的定义为 Tj=ρQ(vj-v0) (24) 式中:Tj是喷口输出总推力;Q是推进泵流量;vj是矢量喷口出口速度;v0是来流速度。输出总推力系数 (25) 式中:Tnum是数值计算所得的输出总推力;Texp为额定工况下参考输出总推力。 网格细化率可以表示为 (26) 式中:Nf和Nc分别是细网格数量和粗网格数量。 表5列出了以网格细化率为1.2生成的4种网格数量不同(G1,G2,G3,G4)对应计算出额定工况(Texp=1 041.638 N)下的推力系数,分别记作S1、S2、S3、S4。 表5 不同网格计算结果Table 5 Results of different meshes 根据文献[30]的研究,网格收敛率〈RG〉的计算方法为 (27) 估计的精度阶数〈PG〉RE由(28)式得到: (28) 渐进范围的距离度量〈PG〉为 〈PG〉=〈PG〉RE/〈PG〉th (29) 式中:〈PG〉th是精度的理论阶数。 网格的不确定度〈UG〉为 (30) 不确定度验证和确认的结果总结在表6中。如表6所示,两组网格的RG都小于1,这表明两组网格单调收敛。此外,网格的不确定性分别为1.1%和2.4%,这表示〈G1,G2,G3〉和〈G2,G3,G4〉网格的精度可以接受。总之,这两组网格呈现出良好的收敛性,后续讨论是基于G2的网格参数进行的。 表6 网格不确定度结果Table 6 Results of mesh uncertainties 5.1.2 Vortex软件仿真可信度分析 因为本文以矢量喷口调整两栖车运动状态的功能为主要研究对象,所以这里选取车体纵倾角作为主要评价对象。 使用STAR-CCM+软件对两栖车辆水中航行姿态进行精细模拟,得到两栖车在水中全速和半速两种工况下的车体姿态数据。将半速行驶下车辆姿态精确计算结果与Vortex软件仿真结果进行对照,并对Vortex仿真系统中阻力、浮力、动升力参数进行微调。验证Vortex软件仿真中3组全速行驶时车辆姿态在同一参数条件下与STAR-CCM+软件仿真结果对应情况,如图10所示。 图10 车辆纵倾角仿真结果对比Fig.10 Comparison of pitch angle simulation results 其中由于不同软件设置方式不同,STAR-CCM+软件仿真纵倾角时,经过一段时间的大幅振荡调整,找到了受力平衡点,车辆状态达到设定工况[31];而Vortex软件在车辆静平衡状态突然施加推力,使车辆状态趋向设定工况。所以在开始阶段纵倾角稍有不同,但也可以看到,最终两种模拟方法的车体纵倾角幅度较为准确的稳定在同一区间内,可以认为Vortex软件仿真结果较为可信。 为预测矢量喷水推进器输出推力与喷口角度的关系,采用随体坐标系Oxyz定义作为仿真坐标系,将矢量喷口的输出总推力T正交分解为轴向推力Tx,偏航推力Ty,俯仰推力Tz,根据轴流泵推力计算公式[19]有 (31) 式中:vjx、vjy、vjz分别是矢量喷口出口速度在3个方向的分量。仿真计算水泵额定工况下,喷口各工况矢量喷水推进器三轴输出推力如图11所示。 图11 推进器仿真输出推力Fig.11 Output thrust in thruster simulation 台架试验结果由三轴测力计给出,图12展示了不同工况下矢量喷口三轴输出推力随喷口俯仰角度变化的曲线。图12(a)对应推进泵转速为944 r/min(两栖车航速1.0 m/s时推阻力平衡点水泵转速)时旋转角度为0°、45°、90°的推进器三轴输出推力;图12(b)对应推进泵转速为1 190 r/min(两栖车航速2.0 m/s时推阻力平衡点水泵转速)时旋转角度为0°/45°/90°的推进器三轴输出推力;图12(c)对应推进泵转速为1 904 r/min(对应两栖车航速2.88 m/s时推阻力平衡点水泵转速)时旋转角度为0°、45°、90°的推进器三轴输出推力。 图12 推进器三轴输出推力Fig.12 Triaxial thrust outputs of thrusters 对比仿真结果和试验结果,在旋转角度β固定、航速不同的条件下,矢量喷口在不同俯仰角度状态时,轴向推力变化规律基本一致,随着水泵转速即输出功率的增加而在数值上增加,这与实际情况相符合。随着水泵输出功率的增加,航速及喷口总推力增加,分解到三轴的推力也随之增加。 理想条件下,当旋转角为0°时,喷口俯仰状态下的总推力T只能分解为Ty和Tz,此时Tx=0 N;当旋转角为90°时,喷口俯仰状态下的总推力T只能分解为Tx和Tz,此时Ty=0 N,这与仿真结果相印证。但是喷口在出口处的流动存在扰动、二次流、回流等不稳定现象,无法按理想情况岀流,因此俯仰状态结果存在相对较小的Tx和Ty。 各工况下x轴推力Tx绝对值随着俯仰角度的增大而先增加后减小,呈抛物线关系,俯状态和仰状态的Tx关于俯仰角0°对称。 β=0°时,y轴推力Ty表现为较小的数值,且也有关于俯仰角0°对称的趋势;β=45°或90°时,y轴推力Ty随着俯仰角度的增大而减小,呈线性关系。 β=90°时,以俯仰角度0°时Tz为零值参考,则Tz随俯仰角度变化较小,且有关于俯仰角0°对称的趋势;β=0°或45°时,z轴推力Tz随着俯仰角度的增大而减小,呈线性关系。 图13给出了不同工况下喷口输出总推力|T|随喷口俯仰角度α变化的趋势。从图13中不同水泵转速的推力曲线可以看出,总推力随俯仰角度变化的趋势呈抛物线关系。随着转速的增加,总推力变化的趋势更加明显。受喷口动作影响,机构结构变动导致喷口推力有一定程度上的损失,各工况最大推力损失如表7所示。推力损失随着推进泵转速增加而减小,随着喷口俯仰角度的增加而增加,仅在(944 r/min-±30°)工况时达到25.5%和38.5%,其余工况损失均在21.7%以下。 图13 输出总推力随旋转角度β变化趋势Fig.13 Trends of total output thrusts with the rotation angle β 表7 各工况最大推力损失 5.3.1 两栖车减摇试验纵倾角验证 仿真实验中对比设置两组仿真计算,第1组喷口俯仰角度与车体俯仰角呈负相关,第2组矢量喷口保持直喷状态,仿真实验中两栖车以航速15 km/h行驶。图14展示了两组仿真实验车体纵倾角的振荡曲线,仿真结果如表8所示。 图14 仿真车体纵倾角变化曲线Fig.14 Simulation results of pitch angle variation 表8 减摇试验仿真结果 从表8中可以看出,第1组纵倾角平均值为-0.76°,第2组纵倾角平均值为2.28°。喷口有控制组比喷口直喷组的车体纵倾角标准差减小约14.4%。 实车试验中,两栖车在航速恒定为2.88 m/s,12 m波长的海浪条件下进行迎浪自航减摇控制试验。试验中保持喷水推进泵转速恒定(1 904 r/min),通过遥控驾驶仪控制喷口的动作。设置两组对照试验,对照组1采用相同条件,对照组2两栖车航速恒定为1.5 m/s(水泵转速恒定944 r/min),12 m波长海浪条件。 车体纵倾角通过DHDAS系统采集,喷口角度通过伺服电机的模拟霍尔传感器反馈到驱动器中的带时间戳的编码器位置获得,根据DHDAS系统记录车体姿态的绝对时间进行两组数据的对齐。第1次实验中,21.5 s前矢量喷口保持直喷,21.5 s后矢量喷口受控开始工作;对照组1中,25 s前矢量喷口保持直喷,25 s后矢量喷口受控开始工作。对照组2中,32.7 s前矢量喷口保持直喷,32.7 s后矢量喷口受控开始工作。减摇试验及其对照组的车体俯仰角变化如图15、图16、图17所示。从图15~图17中可以看到,喷口开始工作后,车体纵倾幅度均会明显降低。因试验结果受人为操作影响,但从试验结果可以看出,喷口受控后,车体纵摇幅度有明显的减小趋势。表9列出了不同工况下两栖车车体纵倾角的均值和标准差。从表9中可以看出,喷口受控后,标准差分别减少约38%、23%、31%。试验及仿真结果都有效说明了矢量喷水推进系统对降低行驶在波浪航况下的两栖车纵倾幅度有显著作用。 图15 两栖车减摇试验结果Fig.15 Amphibious vehicle pitch-reduction experiment results 图16 两栖车减摇试验对照组1Fig.16 Pitch-reduction experiment control group 1 图17 两栖车减摇试验对照组2Fig.17 Pitch-reduction experiment control group 2 表9 减摇试验结果对比 5.3.2 两栖车航向保持试验航向角验证 仿真测试环境为平静无浪海面,对两栖车进行人工方向控制的最大推力直航行驶,行驶距离200 m。观测车辆行驶航向角,对两栖车辆直航性能进行25次重复测试,并进行结果记录和整理,图18为25次试验结果叠图描点法给出的航向角记录。 图18 两栖车辆直航性能仿真实验结果Fig.18 Amphibious vehicle direct-navigation simulation results 在25次直航性能测试中,两栖车辆航向角在±6°的范围内,其中直航偏角最大值为向右偏转5.5°;左右最大偏转角之和为6°。可见两栖车辆在平静水面上的直行能力较为优秀,在航行中会出现少量右偏。 对比仿真结果,两栖车自由自航试验给出了以下结论。图19给出了惯导记录的两栖车在北东地参考系下喷口不受控的航行轨迹拟合曲线以及对应时间内航向角的变化。图20给出了喷口受控的航行轨迹拟合曲线以及对应时间内航向角的变化。在自由直航试验中,喷口不受控时,车体偏向某一侧,航向角不会回正;喷口受控时,车体在横向极限位移不超过0.6 m,两栖车在航向角变化在±50°内波动,因为手动调节喷口转角,在修正方向时容易出现人为的超调,从而导致航向角的来回波动。上述仿真计算和试验研究的结果,验证了安装在无人两栖车上的矢量喷水推进系统具有对两栖车进行航向调节、航向保持的功能。 图19 两栖车不受控直航轨迹及航向角曲线Fig.19 Uncontrolled direct-navigation experiment trajectory and heading angle profile of an amphibious vehicle 图20 两栖车受控直航试验轨迹及航向角曲线Fig.20 Controlled direct-navigation experiment trajectory and heading angle profile of an amphibious vehicle 本文针对我国国防领域水面高速稳定的水陆两栖车的研制需求,设计具备对水陆两栖车进行航向保持和姿态调整功能的矢量喷水推进器。利用CFD/Vortex联合仿真和水池试验研究了装配在两栖车上的矢量喷水推进器的减摇功能和航向保持功能。得出以下主要结论: 1)矢量喷水推进器三轴输出推力随着水泵转速的增加而增加。总推力大小随喷口旋俯仰角度变化呈抛物线趋势,在0°时取得最大值。喷口的推力损失随转速的增加而减小,除个别工况(944 r/min-±30°:25.5%/38.5%),推力损失均在21.7%以下。 2)仿真结果给出在15 km/h航速下矢量喷水推进器可以降低两栖车约14.4%的车体纵摇角标准差;通过对比两次施加喷口控制与否的试验数据,可以得到在12 m波长,2.88 m/s航速工况下,矢量喷水推进器在略微提高纵倾角均值的情况下(1.52%;2.76%),有效降低两栖车的车体纵摇幅度(标准差降低38%/23%)。在12 m波长、1.5 m/s航速工况下,矢量喷水推进器同时降低两栖车的纵倾角均值(40%)和纵摇幅度(标准差降低31%)。矢量喷水推进器对两栖车具有一定的减摇功能。 3)在验证矢量喷水推进器的航向保持功能时,25次直航仿真实验中最大偏航角小于6°,两栖车自由自航试验中两栖车车体横向最大位移不超过0.6 m,航向角受喷口控制人工超调影响在±50°内波动。因两栖车在试验中的横向位移保持在一定范围内,矢量喷水推进器对两栖车具有一定的航向调整保持能力。2.3 求解设置


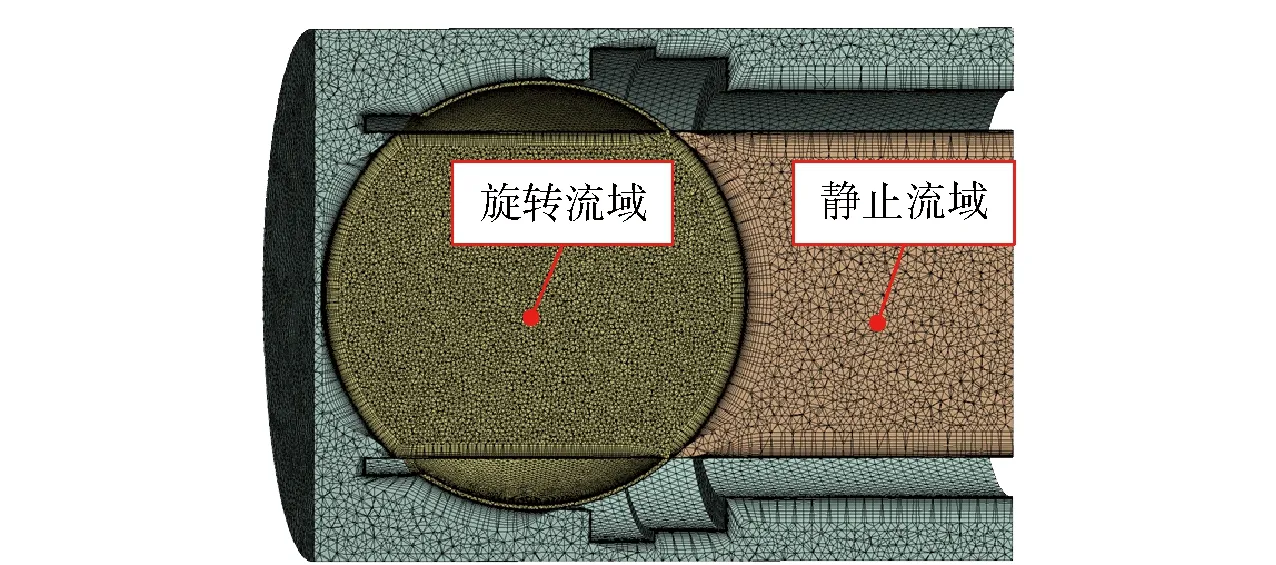
3 Vortex数值计算
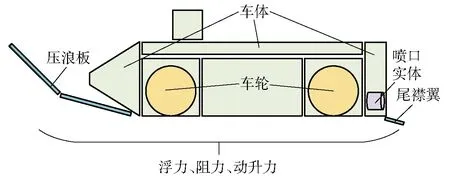
4 矢量两栖车试验
4.1 矢量喷口台架试验
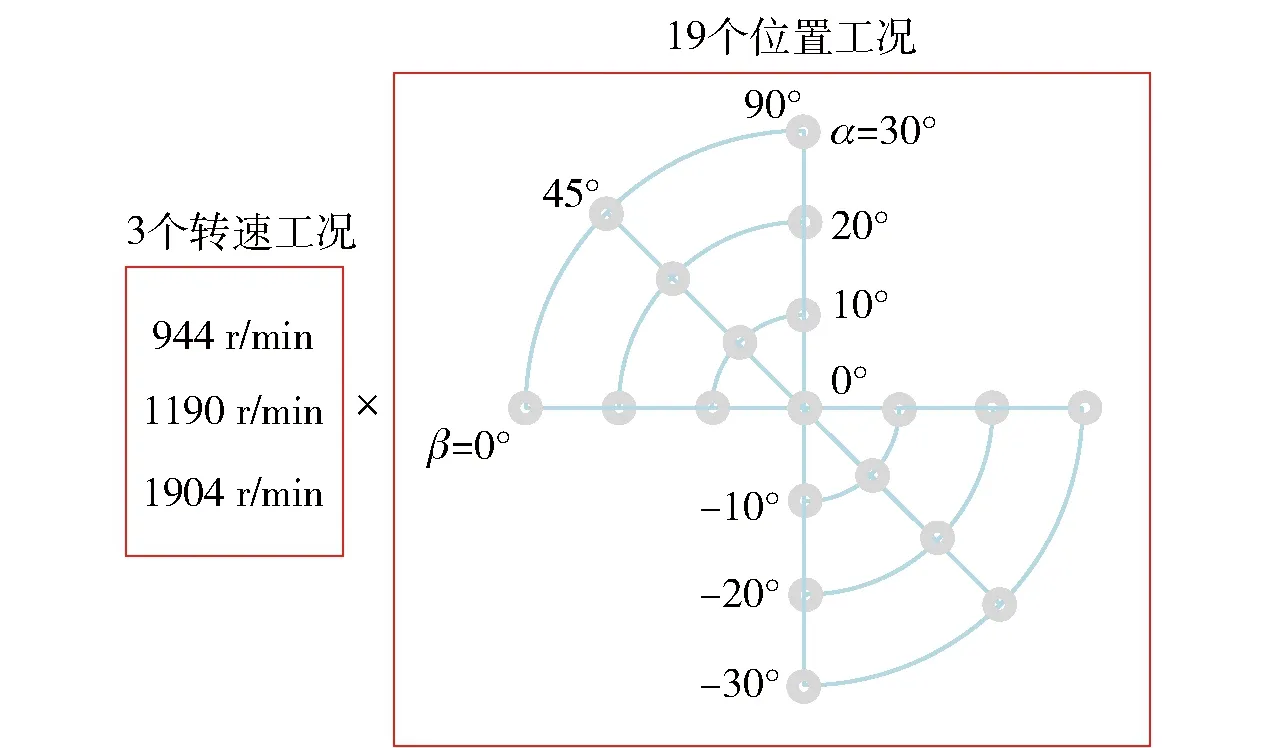
4.2 强制自航减摇试验

4.3 自由自航航向保持试验

5 仿真与试验结果分析
5.1 仿真可信度分析
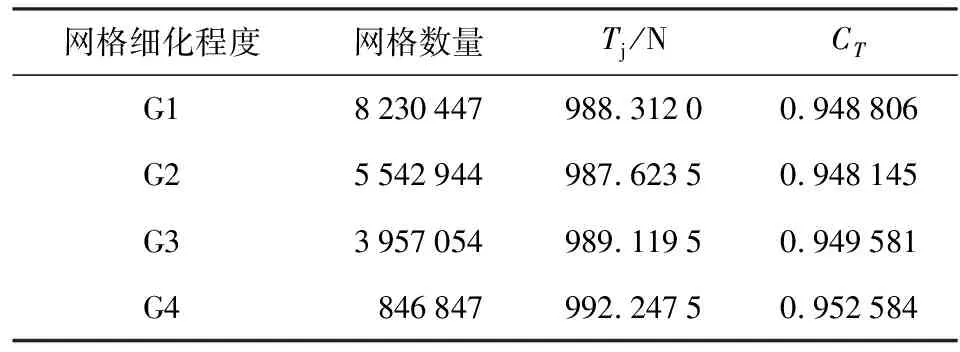

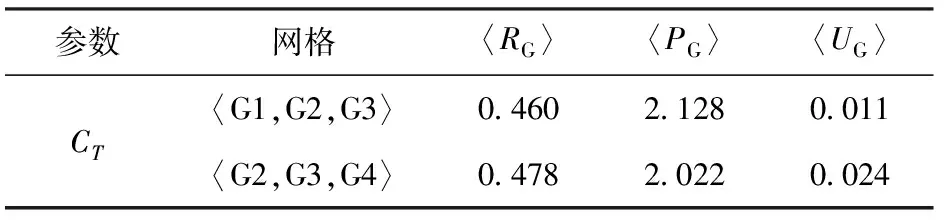
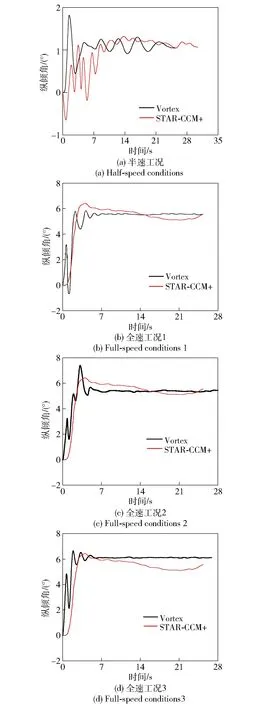
5.2 矢量喷水推进器输出推力分析

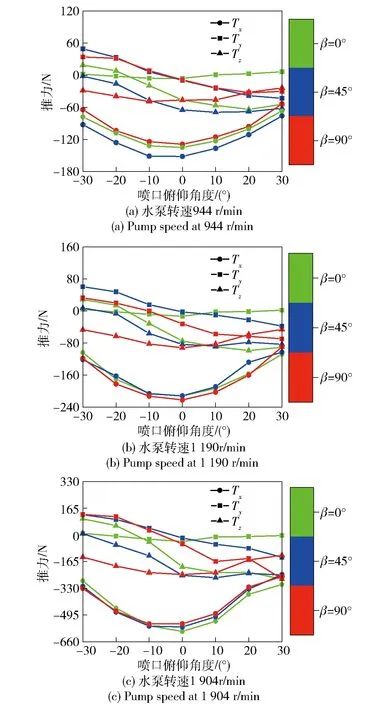


5.3 两栖车航向角和纵倾角验证


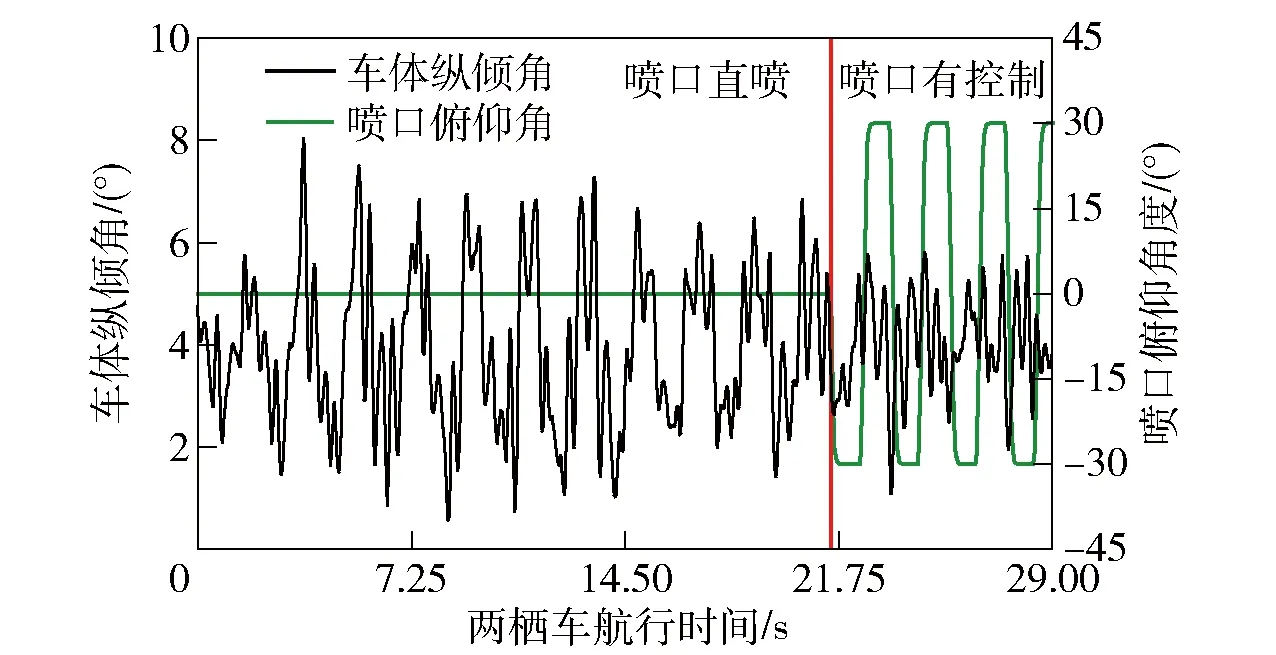
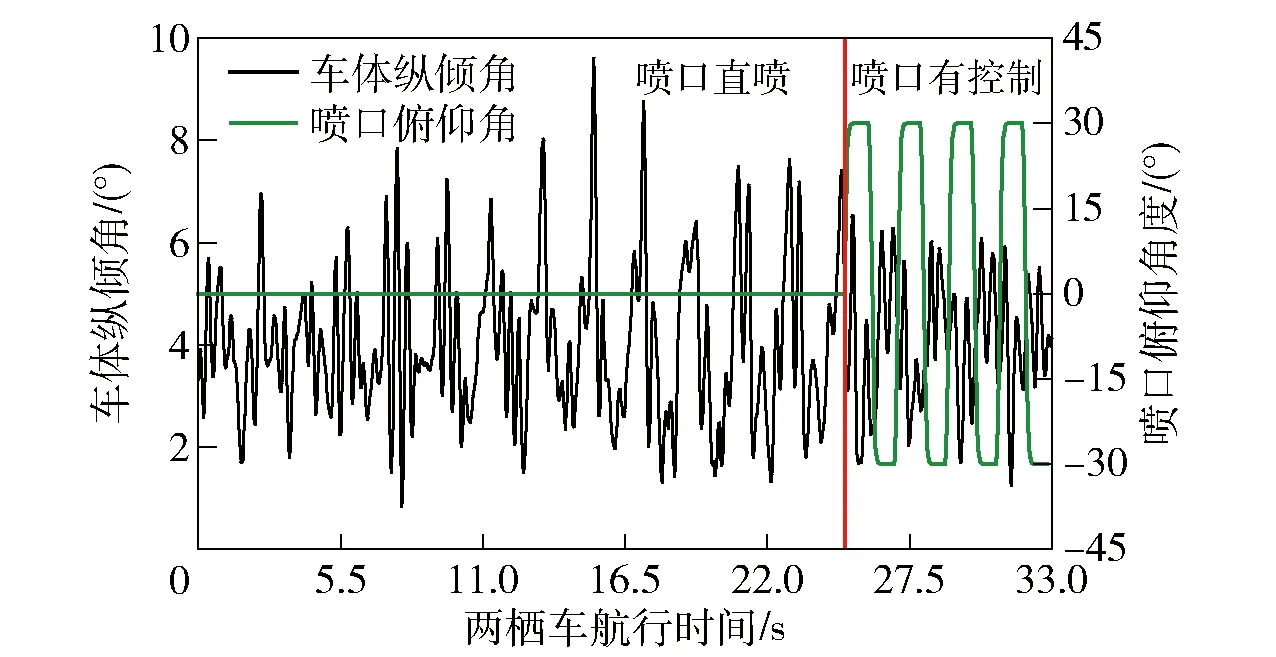

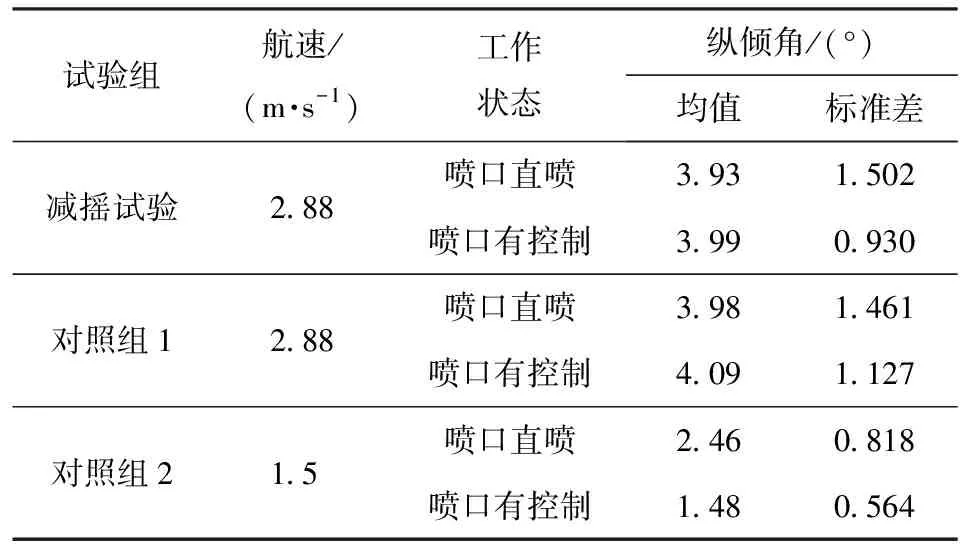
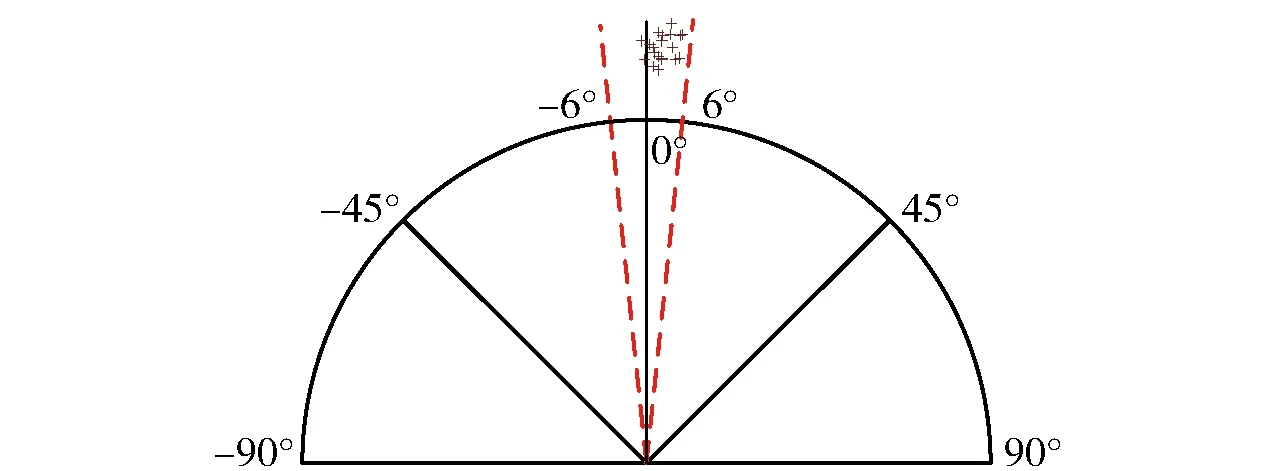
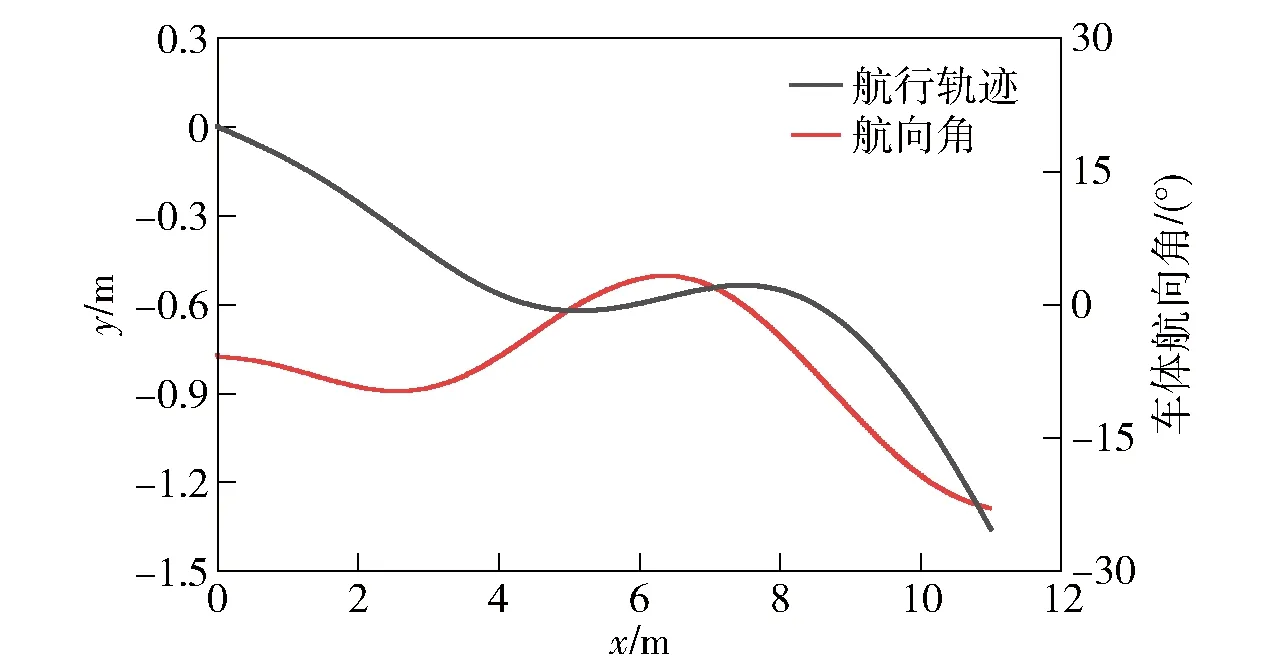

6 结论

