高速铁路典型无砟轨道的桥梁噪声特性分析

杜 淼，王开云，閤 鑫，张晓芸，杨 力

（1.兰州交通大学 机电工程学院，兰州730070；2.兰州交通大学 甘肃省轨道交通服役环境与智能运维重点实验室，兰州730070；3.西南交通大学 牵引动力国家重点实验室，成都610031）

近年来，随着高速铁路网的不断扩大及高速列车运行速度的不断提升，伴随而来的环境振动与噪声问题不断凸显，已对沿线居民的生活产生了困扰［1-2］.其中针对混凝土桥梁低频噪声源的探究及其降噪措施的研究已成为研究热点之一.

在对高速铁路高架线路不同轨道结构类型的噪声研究方面，在针对CRTSⅠ型无砟轨道的研究中，张小安［3-4］等对桥梁-声屏障系统内噪声分布特性进行研究，探寻其有无声屏障时的振动与噪声分布规律.在CRTSⅡ型无砟轨道方面，肖慧娟［5-6］等探讨轨道系统振动与噪声之间的相干性，对其减振降噪效果进行参数优化.雷晓燕［7］等通过建立1/10无砟轨道箱梁桥，将阻尼板至于箱梁翼缘板、腹板等位置进行降噪试验.王平［8］等在高架线路内的轨道下安装橡胶垫，长期跟踪分析其对车内、轨道系统、桥梁及地面的振动噪声影响.在对CRTSⅢ型无砟轨道的研究中，李佳静［9］等基于车辆-无砟轨道-下部基础振动噪声联合分析模型，根据轨道结构的刚度匹配对其减振降噪效果进行分析.宋瑞［10］等对减振与常规两种CRTSⅢ型无砟轨道下桥梁的振动与噪声特性进行对比分析，认为减振型轨道能有效降低桥梁结构噪声.张迅［11］等对铺设CRTSⅡ型和Ⅲ型无砟轨道-混凝土简支箱形梁桥和其他混凝土简支槽形梁桥、钢-混组合连续板梁桥的噪声实测与仿真数据进行对比，对车速、车型、桥型与其噪声之间的关系展开研究.

既有研究表明，轨道结构对高速铁路振动能量的传递有着很好的抑制作用［12-13］，且典型无砟轨道已广泛应用于高速铁路中.但目前鲜有系统研究高速铁路典型轨道结构对轨道—桥梁系统振动能量和桥梁噪声的影响研究，因此有必要针对三种典型轨道结构下的高架线路噪声展开研究.本文选取国内典型的三种板式无砟轨道，建立轨道—桥梁有限元模型，以时域轮轨力作为输入，求解列车载荷下系统的振动响应，并基于功率流分析方法研究其能量传递特性；进一步建立桥梁声学边界元模型，以桥梁振动响应作为边界条件，分析桥梁结构噪声特性.通过分析频域内轨道—桥梁系统的振动能量传递特性及桥梁声场声压级特性，揭示不同类型板式轨道的减振降噪效果差异，为高速铁路轨道选型设计提供参考.

1 典型板式无砟轨道介绍

我国高速铁路常见的板式无砟轨道主要包含CRTSI型、CRTSII和CRTSⅢ型三种类型（下文分别简称为I型、II型和Ⅲ型轨道），主要由钢轨、弹性扣件、轨道板、填充层、底座等部分组成，如图1所示，关键部件的尺寸和材料类型参见表1.

图1 典型板式无砟轨道结构示意图Fig.1 Structure schematic diagram of typical slab ballastless tracks

在轨道板与底座的定位方式方面，I型轨道采用定位凸台并充填树脂，Ⅱ型轨道在桥上铺设时采用侧向挡块和两布一膜滑动层，Ⅲ型轨道采用限位凸台和中间隔离层.在结构方面，I型和Ⅲ型轨道使用单元式轨道板，Ⅱ型轨道采用纵连式轨道板；I型和Ⅱ型轨道的填充层均为水泥乳化沥青砂浆（CA），但配比有所差异，Ⅲ型填充层为配筋的自密实混凝土（SCC）.

2 仿真模型

2.1 无砟轨道-桥梁有限元模型

依据典型无砟轨道及桥梁的结构特点，建立其有限元模型，结构关键尺寸参数见表1.三种轨道的底座与轨道板均采用Solid45实体单元进行模拟，钢轨采用Beam188梁单元模拟，而扣件系统简化为弹簧阻尼单元，采用Combin14单元模拟.Ⅰ型和Ⅲ型轨道在单跨桥上均铺设6块5.6 m长的单元板，板间间距为70 mm，而II型轨道采用30 m通长板.Ⅰ型和II型轨道中CA砂浆层考虑为弹簧阻尼单元，同样采用Combin14单元进行模拟；对于Ⅲ型轨道，其SCC填充层为C40混凝土，模型中采用Solid45实体单元进行模拟.桥梁选取常见的32 m跨度高速铁路双线混凝土简支箱梁桥，其桥梁截面如图2所示，采用Shell63壳单元对其进行模拟.三种板式无砟轨道和桥梁模型中关键参数见表2.

表2 不同板式无砟轨道模型关键参数Tab.2 Critical parameters of different slab ballastless track models

图2 32 m简支箱梁横截面图Fig.2 Cross section diagram of 32 m simply-supported box girder

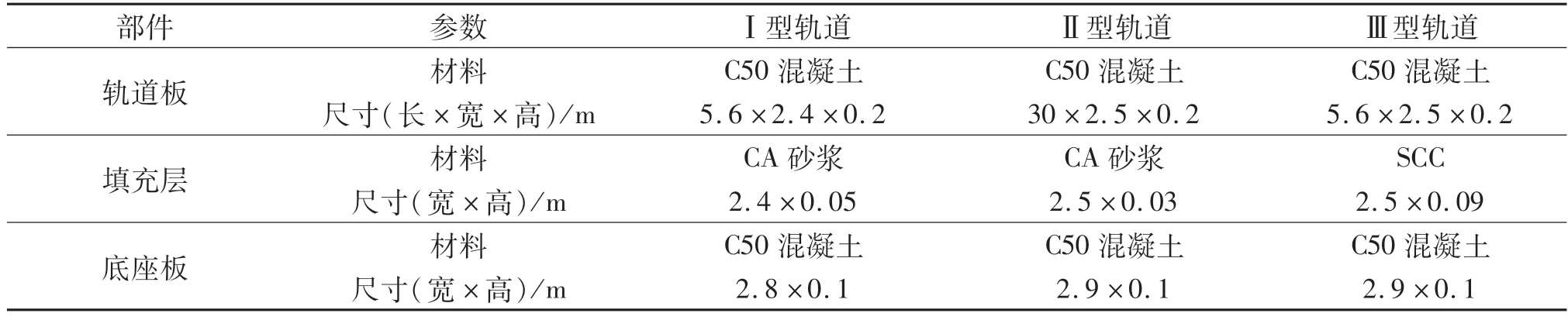
表1 不同类型板式无砟轨道关键部件尺寸和材料Tab.1 Critical sizes and materials of key components for different types of slab ballastless track

2.2 声学边界元模型

利用Virtual.Lab软件建立与有限元模型对应的桥梁声学边界元模型，设置距桥梁底板10 m高的刚性障板考虑地面的反射作用，并在桥梁跨中位置建立30 m×23 m的横向声场，如图4所示.以桥梁的振动响应作为声学边界条件分析不同轨道结构的桥梁声辐射特性.

图3 三种典型板式无砟轨道有限元模型Fig.3 Finite element models of three typical slab ballastless tracks

图4 桥梁声学边界元模型Fig.4 Acoustic boundary element model of the bridge

3 基于功率流方法的振动能量传递特性分析

本节以某型高速动车为例，基于车辆—轨道—桥梁耦合动力学模型，不平顺选取中国高速无砟谱，速度设置为250 km/h，仿真计算得到时域轮轨力；以时域轮轨力作为轨道-桥梁有限元模型输入，计算系统振动响应；进一步结合功率流理论，分析振动能量传递特性.车辆动力学参数参见文献［14］.

3.1 功率流理论

功率流是研究复杂系统内振动能量传递与分布规律的常用方法［15］，其在频域内的计算公式为

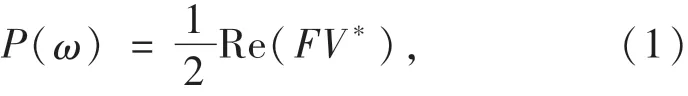
式中，F与V分别为力和速度在频域的复数值，F=F0ejω，V=V0ejω；Re表示取实部，上标*表示取共轭；P（ω）为功率流，N·m/s.

在频域内，频率k下区域内n个节点的总功率流P（k）可表示为

式中，i为节点序号；Vi（k）和Fi（k）分别为频率k下的节点i的节点速度和力.

为了表征由上层结构传递到下层结构的能量比例，采用功率流传递率来体现路径上的能量衰减性能，功率流传递率Rt为

式中，Pu（k）为系统连接中下层结构的功率流；Pd（k）为上层结构的功率流.

选取桥梁跨中位置的单块轨道板（纵连式II型轨道选取长度为5.6 m的区域），提取区域内钢轨、轨道板及桥梁顶板的所有节点处的力和速度，基于式（1）～（3）可计算系统内振动能量分布及传递特性.

3.2 典型轨道的功率流分析

图5展示了三种无砟轨道-桥梁模型中钢轨、轨道板和桥梁的功率流的分布规律.由于桥梁噪声研究重点关注低频区域，此处选取20～200 Hz范围内进行分析［16］.

以I型轨道-桥梁系统为例，图5（a）展示了钢轨、轨道板及桥梁的功率流，其中振动能量在传递过程中逐步衰减，表明轨下胶垫和填充层在低频范围内能更好的储存和耗散能量.三种结构的功率流在80～200 Hz内均随着频率增加而减小，且在全频段 内存在波动现象.

图5 无砟轨道-桥梁系统内各部件功率流Fig.5 Power flow of each component in the ballastless track-bridge system

由于钢轨功率流为系统输入功率流，受轨下各减振层影响较小，三种轨道模型中钢轨功率流整体差异较小，如图5（b）所示.由图5（c）可知，在20～75 Hz频率范围内，三种轨道板的功率流差异较小；在75～200 Hz频率范围内，I型轨道板功率流值显著大于其余两种轨道板，表明该型轨道板累积更多的振动能量，而II型板和Ⅲ型板功率流值整体较为接近.从图5（d）中可以看出，采用Ⅲ型轨道的桥梁，其最大功率流出现在32 Hz处，而采用I型和II型轨道的桥梁，其最大功率流均出现在80 Hz附近.此外，采用Ⅲ型轨道的桥梁，其功率流在50 Hz以上频率范围内显著更小.

为了更直观的展示不同类型轨道-桥梁系统中的振动能量衰减特性，基于式（3）计算钢轨-轨道-桥梁间的功率流传递率，如图6所示.从图6（a）可以看出，三种无砟轨道中从钢轨到轨道板的功率流传递率在20～110 Hz频率范围内较为接近；在110～200 Hz频率范围内，I型轨道中从钢轨到轨道板的功率流传递率整体较其余两种更大，而II型和Ⅲ型轨道传递率接近.由图6（b）可知，三种轨道模型中从轨道板到桥梁的功率流传递率均在0.75附近，但II型和Ⅲ型轨道模型中传递率的波动范围更大.

图6 无砟轨道-桥梁功率流传递率Fig.6 Power flow transfer rate in the ballastless track-bridge

4 不同轨道型式桥梁噪声特性

本节进一步基于声学边界元模型，研究不同轨道型式桥梁结构噪声在不同场点辐射噪声的变化规律.在图4声场中选取桥下（SF1）、桥下远点（SF2）、桥侧（SF3）及桥上（SF4）四处典型场点，对其1/3倍频程线性计权声压级（SPL）进行分析.图7（a）～（d）展示了三种轨道模型声场典型场点处声压级.

由图7（a）可知，采用I型、II型和Ⅲ型轨道的桥梁在SF1处SPL的最大值均出现在80 Hz处，分别为67.2 dB、66.2 dB和63.3 dB，结合图5（d）可知，噪声峰值优势频率与桥梁功率流峰值频率一致.在31.5～125 Hz范围内，采用I型和II型轨道的桥梁在该场点处SPL差异极小，而采用Ⅲ型轨道的桥梁对应的SPL在31.5 Hz和40 Hz处较其余两种更大.与SF1场点处相同，SF2处SPL的优势频率为80 Hz，对应的峰值分别为65.6 dB、65.6 dB和71.8 dB，如图7（b）所示.其中，采用I型轨道的桥梁在该场点的SPL与II型轨道接近，仅在100 Hz处相差约12.7 dB，而采用Ⅲ型轨道的桥梁SPL在31.5 Hz、80 Hz及100 Hz处较其余两种的相应值更大.

从图7（c）可以看出，在SF3处，采用I型和II型轨道的桥梁下SPL较为接近，仅在100 Hz和200 Hz处相差约5～6 dB，其优势频率均为50 Hz，SPL值分别为74.7 dB和73.5 dB；采用Ⅲ型轨道的桥梁下SPL整体较采用I型和II型轨道的桥梁场点SPL更小，其优势频率在40～63 Hz范围内，最大SPL约为68 dB.在SF4处，采用I型和II型轨道的桥梁下SPL优势频率与SF3处相同，但SPL值增大约8 dB，而采用Ⅲ型轨道的桥梁其优势频率为40 Hz，SPL约为78.8 dB，见图7（d）.与采用I型和II型轨道的桥梁相比，采用Ⅲ型轨道的桥梁在31.5 Hz和40 Hz处的SPL较大，而在50～80 Hz频率范围内更小.

图7 三种无砟轨道模型声场典型场点声压级对比Fig.7 Comparisons of SPLs at typical points in the sound field for three ballastless track models

综上可知，采用I型、II型和Ⅲ型轨道的桥梁在桥下区域的辐射噪声整体差异较小，而采用Ⅲ型轨道的桥梁在桥下远点区域的辐射噪声较采用其余两种轨道的桥梁略大；采用I型和II型轨道的桥梁在桥上和桥旁区域的辐射噪声相近，而采用Ⅲ型轨道的桥梁在该区域降噪效果更优.

5 研究结论

本文建立了I型、II型和Ⅲ型轨道—桥梁有限元模型和声学边界元模型，研究了轮轨载荷作用下系统内振动能量传递及桥梁声场声压级特性，并对比分析了采用不同板式轨道桥梁的声振特性，结论如下：

1）II型和Ⅲ型轨道板功率流整体一致，而I型轨道板功率流在75～200 Hz频率范围内较之更大；对于采用I型和II型轨道的桥梁，其功率流在50～200 Hz频率范围内较采用Ⅲ型轨道的桥梁略大，相应频率范围内的桥梁辐射噪声也越大.

2）采用I型和II型轨道的桥梁整体辐射噪声相近，而采用Ⅲ型轨道的桥梁在桥上与桥旁区域降噪性能更优，但在桥下远点区域略差.