阀控半主动减振器模糊控制策略研究

董世昌，孟建军，宋彩云，郑 堃，毛 元

（1.兰州交通大学机电技术研究所，兰州 730070；2.南京工程学院汽车与轨道交通学院，南京 211167；3.正德职业技术学院汽车与机电工程系，南京 211106；4.江苏省先进数控技术重点实验室，南京 211167；5.国网南京市江北新区供电公司，南京 211800）

车辆的悬架，除了要实现机械支撑和连接的作用，当适当地设计来减少车辆的振动.根据应用的减振方法，可以区分三种类型的悬架：被动、半主动和主动.被动悬架不使用任何额外的力，具有不变的刚度和阻尼，其应用效果显著而且十分广泛.然而，被动悬架参数必须在安全性和驾驶舒适性之间提供一个固定的取舍.在半主动悬架中，悬架的刚度可以在行驶过程中发生变化.与被动悬架不同，半主动悬架可以在线适应不同的工况.它可以提高安全性和驾驶舒适性.与主动悬架控制相比，它所涉及的能量要小得多，而主动悬架控制需要作动器产生额外的力，从而最大限度地减少振动.所以半主动悬架也有较多的应用［1-3］.相对电磁阀控减振器和磁流变减振器，虽然转阀控制减振器的响应时间较慢，但是由于转阀控制的减振器阻尼变化较为线性，所以产生的抖动也较少，所以转阀控制的半主动减振器仍然有其适用的场景.国内外学者对半主动悬架以及半主动减振器的控制进行了大量研究［4-6］.

模糊逻辑控制近些年发展迅猛［7-9］.它的主要优点在于当数学模型不完全已知时，它对系统的适用性强.有些学者针对四分之一车模型提出模糊逻辑控制器，其输入信号为悬架挠度及其变化，输出为控制信号的变化［10-12］.有学者通过模糊方法来解决半主动悬架的乘坐空间和悬架空间的取舍，他们研究的目标是将车身垂直加速度降至最低，避免撞到悬挂限制［13］.Zheng等人提出了一种基于时域变化的模糊控制策略［14］，其中主动控制为两种控制的结合，前者以车身加速度为主要部件获得，后者以模糊逻辑为补充控制获得.陈龙等人根据减振器处于拉伸或者压缩以及各自的趋势状态，设计了新的模糊半主动悬架控制方法［15］.李子璇等人建立了高精度非线性空气弹簧气室模型，运用模糊PID算法对悬架系统进行控制，达到了良好效果［16］.葛宇超等人验证了馈能磁流变半主动悬架模糊滑模控制的有效性［17］.徐绍勇等人采用模糊最优控制算法结合机器学习，有效地控制了汽车半主动悬架［18］.模糊控制方法在机械领域的应用还有很多，比如机器人等自动化领域［19-20］.

本研究的目的是利用转阀控制半主动悬架改善乘客的乘坐舒适性.阀控式半主动减振器由步进电机驱动阀芯转动，从而改变活塞腔节流口的面积，节流口一般分为可调部分和固定部分，如图1所示，这种结构的可调部分就比较适合模糊控制.本文提出了一种模糊控制方案，通过一个模糊逻辑单元，根据被控系统的状态，找到转阀控制半主动减振器阻尼比能够快速响应的区间.最后通过仿真分析发现该控制器在控制车身振动、鲁棒性、功耗、保持悬架工作空间等方面有较好的效果.

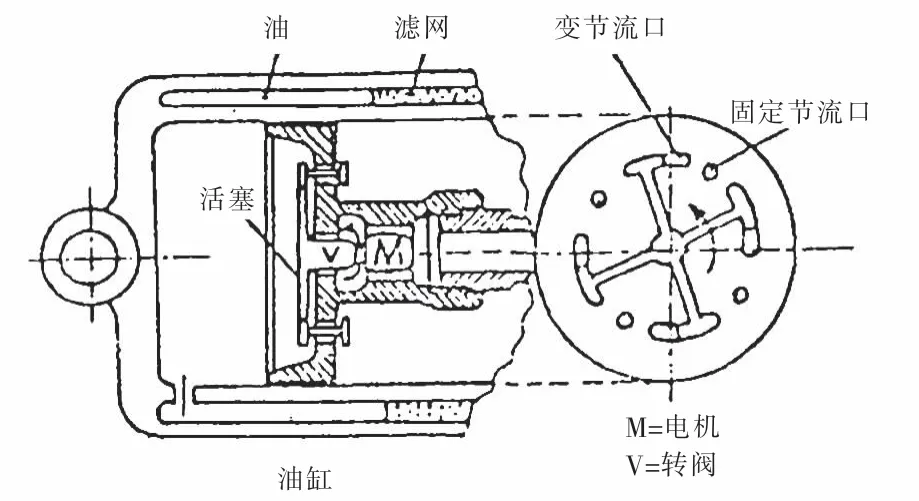
图1 阀控式半主动减振器结构Fig.1 The structure of valve controlled semi-active shock absorber

1 系统框图

在电控的范围内讨论阀控半主动悬架的控制，是指对半主动减振器阻尼比的控制，实质上是对半主动减振器变节流口开度的控制，通过调节转阀的开度来控制目标所需的阻尼比［21-23］.当汽车运行时，传感器检测到活塞杆位置和阻尼力，计算出悬架系统的阻尼比，根据车速由ECU分析处理确定转阀步进电机的调节步数来控制阻尼比.如图2所示是模糊控制系统结构图.

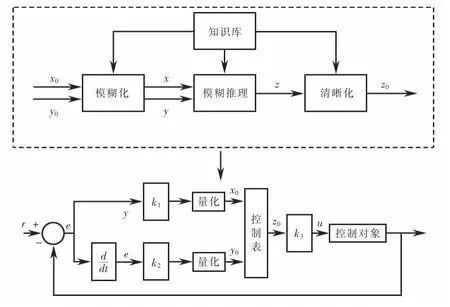
图2 模糊控制系统结构框图Fig.2 Structure block diagram of fuzzy control system

设e，de和u的变化范围为［-e*，e*］，［-de*，de*］和［-u*，u*］，同时设e，de和u的论域为｛-ni，…，-1，0，1，…，ni｝（i=1，2，3）

则

因为x0，y0的个数有限，所以可以将他们的所有可能的情况先计算出来，把计算的结果作为控制表.控制过程中只要查询控制表就可以由x0，y0求得z0，然后在进行比例变换，变成我们所需的控制量.

设ζ0为减振器的目标阻尼比，阻尼比ζ（k），ζ（k-1）为本次和上次的采样值，其时间间隔为Δt，则本次和上次的阻尼比误差值为：

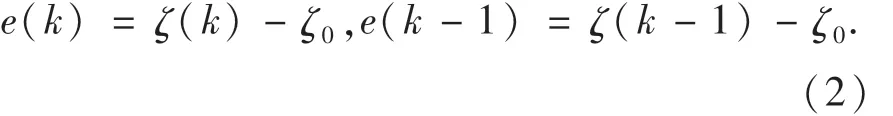
本次的阻尼比误差率为：

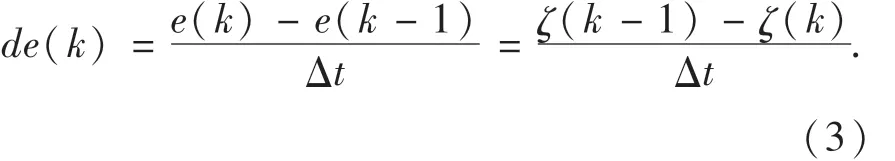
量化因子k1和k2是输入变量误差及其误差变化率的加权程度，其大小对系统的动态特性响应有很大的影响，应慎重选择.

2 控制系统的数学模型

半主动减振器的建模与仿真是减振器设计特别是半主动减振器控制系统设计的必要途径.在计算机的仿真实验研究中，为了实现半主动减振器的阻尼比控制，必须先获得减振器控制系统的数学模型，然后在此数学模型的基础上，采用模糊控制实现阻尼比的控制.尽管设计的模糊控制器不需要阻尼比变化的数学模型，但是模仿减振器的阻尼比控制系统还是需要其近似的数学模型［24］.

减振器工作在我们所需的阻尼比附近时，阻尼比的大小会受到转阀的开度，减振器的伸缩速度等因素的影响，从控制理论上来说，阻尼比控制具有明显的非线性、时变性和不确定性.因此，很难建立一个精确的阻尼比控制系统的数学模型.如图3所示是近似过的阻尼比控制系统的动态数学模型.然后根据实验台架采集的输入和输出数据，由Matlab进行系统辨识推导出该系统的模型.

图3 阻尼比控制的动态模型Fig.3 Dynamic model of damping ratio control

已知转阀的开度（0%～100%）与执行机构的步进电动机输出（0～128步）的关系近似为一条直线，所以可以用比例环节来近似表示其数学模型：

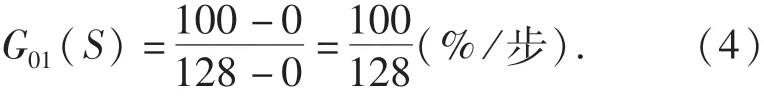
阻尼比随着活塞杆的速度变化呈非线性变化，只有在活塞速度较大时呈现较好的线性，以此来近似表示减振器的阻尼比，可以利用实验测得阻尼比变化与转阀开度的关系，不妨设其关系如表1所示.

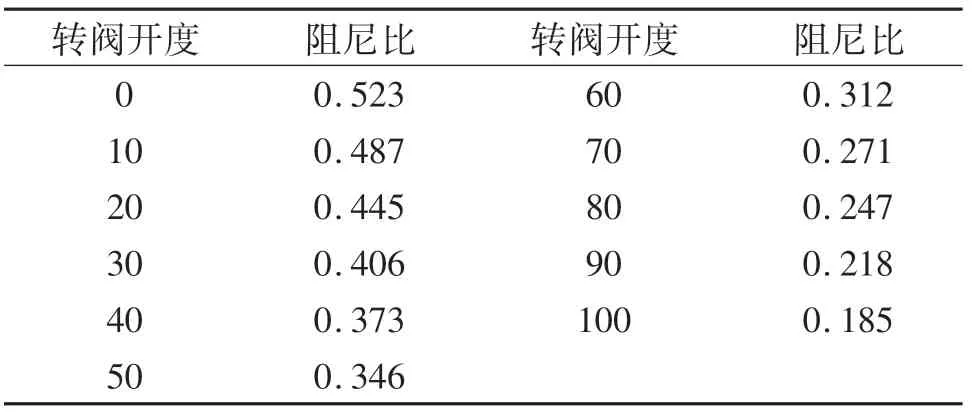
表1 减振器转阀开度与阻尼比的关系Tab.1 The relation between the opening degree and damping ratio of shock absorber rotary valve

根据实际系统需要的阻尼比为0.346时，其转阀开度为50%［15］，在工作点附近，转阀开度与阻尼比的关系近似为二阶系统模型，最后计算出系统对应的脉冲传递函数.

3 模糊控制器的设计

阻尼比控制是指对车辆运行时的减振器阻尼比ζ的控制，实际上是通过调节转阀的开度来改变油缸中液体通过的难易程度来实现目标所需的阻尼比ζ0.控制时，把ζ当作系统的反馈值，将实际值偏离目标阻尼比ζ0的大小e（e=ζ0-ζ）当作调节方向的依据之一，同时为了让系统更稳定，同时减小超调量和抖振现象，把误差变化率de也作为控制调节量和方向的依据.所以，模糊控制器是以阻尼比误差e和误差率de作为输入量，以转阀步进电机的工作步数u作为输出量.误差变化率de的变化范围定为［-0.1，+0.1］.步进电机的工作步数范围［0，+128］步.

将误差、误差变化率和输出变量的模糊集按如下进行划分

因为阻尼比的变化范围为：e*∈［-0.25，+0.25］，其模糊论域为：e∈［-6，6］，

因此，阻尼比误差的量化因子为：

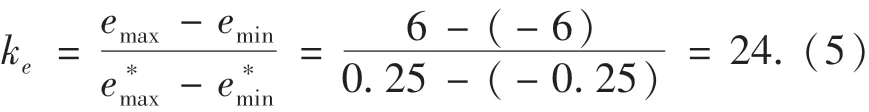
可得误差率量化因子为：

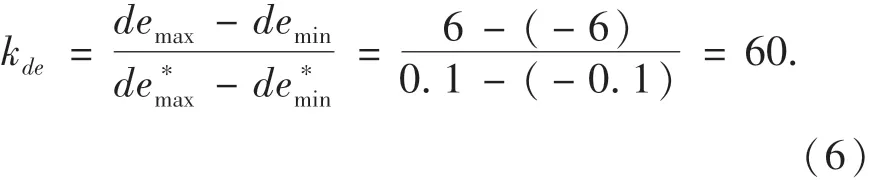
输出的量化因子为：

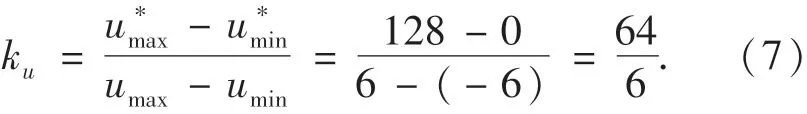
对于实际的阻尼比误差量进行线性变换，线性变换公式：

同理可得误差变化率de的线性变换公式为：

阻尼比误差、阻尼比误差变化率和步进电机工作步数的模糊变量分别用e、de、u来表示，通常把模糊语言变量值阻尼比误差e和步进电机的工作步数u取成7个模糊子集，即：

输入模糊语言变量e和输出模糊变量u隶属度函数如图4所示.

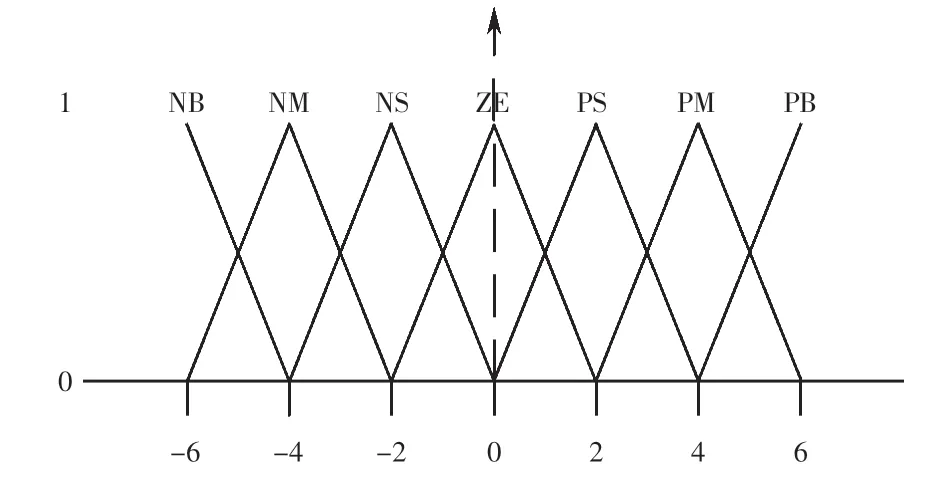
图4 语言变量e和u隶属度函数Fig.4 Membership functions of language variables e and u

模糊变量误差变化de的隶属度函数如图5所示.

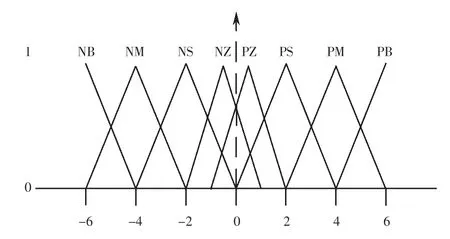
图5 模糊变量de隶属度函数Fig.5 Membership function of fuzzy variable de

当阻尼比误差为负大NB时，控制量的变化应取负大NB，以快速减小阻尼比.当阻尼比误差为负大NB时，选择的控制量为不变ZE，以平稳减小阻尼比.最后可以得出56条控制规则.

六组学生观看聋哑演员排列整齐、动作一致地将《千手观音》表演得美轮美奂的视频，思考聋哑演员是怎样实现自我发展的？

系统的模糊控制规则一共有56条规则，因为e的模糊分割数为7，de的模糊分割数是8个，所以规则囊括了最大可能的规则数.通常情况下规则数可以少于56个.其控制规则依次为

R1：如果e是NB and de是NB则u是NB

R2：如果e是NB and de是NM则u是NB

…

R56：如果e是PB and de是PB则u是PB

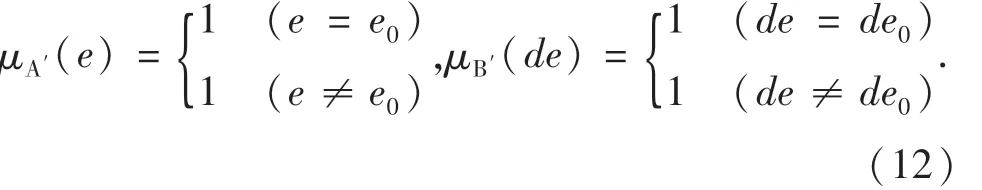
式中：e0和de0为已知输入.

根据模糊推理的方法和性质，可以很容易求得输出量的模糊集合C′为：

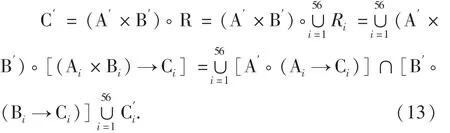
可以用Matlab计算出当e，de不同组合的时候其对应的输出量u.采用线性变换就可得到步进电机的实际控制量u*为：

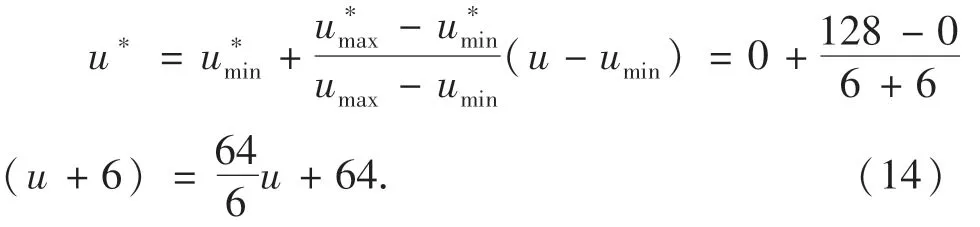
4 系统的仿真实验

将建立好的阻尼比控制数学模型导入Matlab进行仿真，当系统设定阻尼比的给定值在0.35到0.45之间变化时，系统的阻尼比可以快速地跟踪其变化，如图6所示.

从图6可以看出阻尼比控制在0.35时的稳态误差较大，实际工程中一般也很少只采用模糊控制一种方法，加入传统的PID控制的效果如图7所示，可以有效地减小稳态误差，控制效果进一步提升.

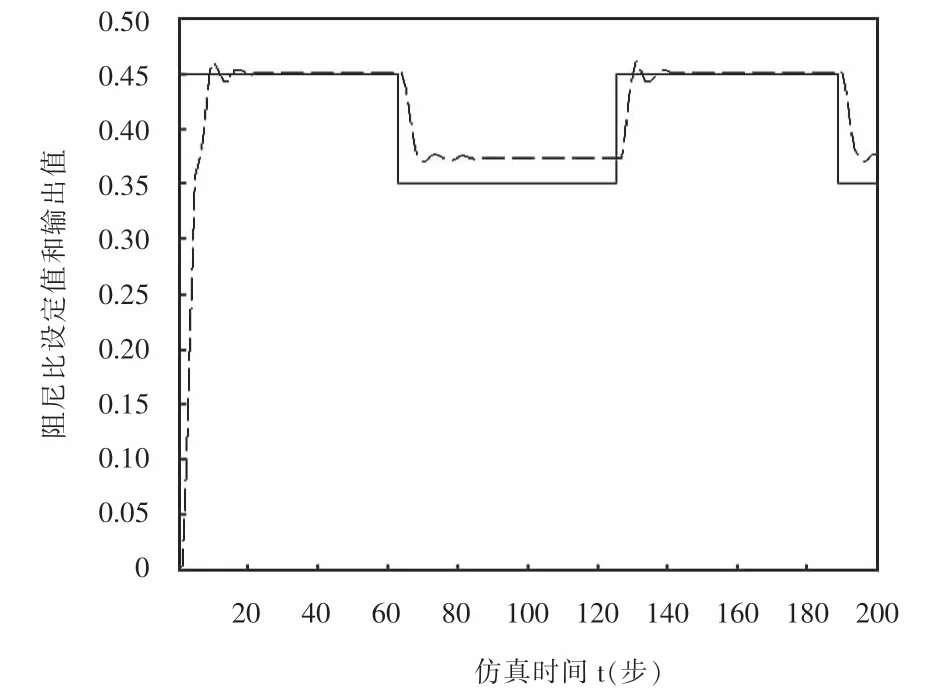
图6 模糊控制阻尼比跟踪曲线Fig.6 Damping ratio tracking curve of fuzzy control

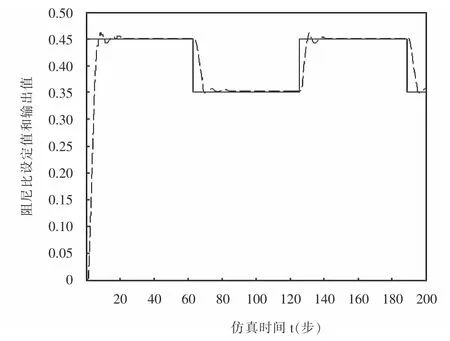
图7 模糊PID控制阻尼比跟踪曲线Fig.7 Damping ratio tracking curve of fuzzy-PID control

根据经典的汽车1/4半主动悬架动力学模型，若悬架处于拉伸状态，且具有进一步拉伸的趋势，或者悬架处于压缩状态，且有进一步拉伸趋势，选取减振器阻尼比为0.45.若悬架处于拉伸状态，但存在压缩趋势，或者悬架处于压缩状态，但存在拉伸趋势，选取减振器阻尼比为0.35.若悬架动行程和垂向速度都比较小，选用半主动减振器阻尼比为0.2.那么随机路面激励下的悬架响应如图8所示.

从图8可以看出阀控式模糊半主动控制有效改善了悬架的性能.

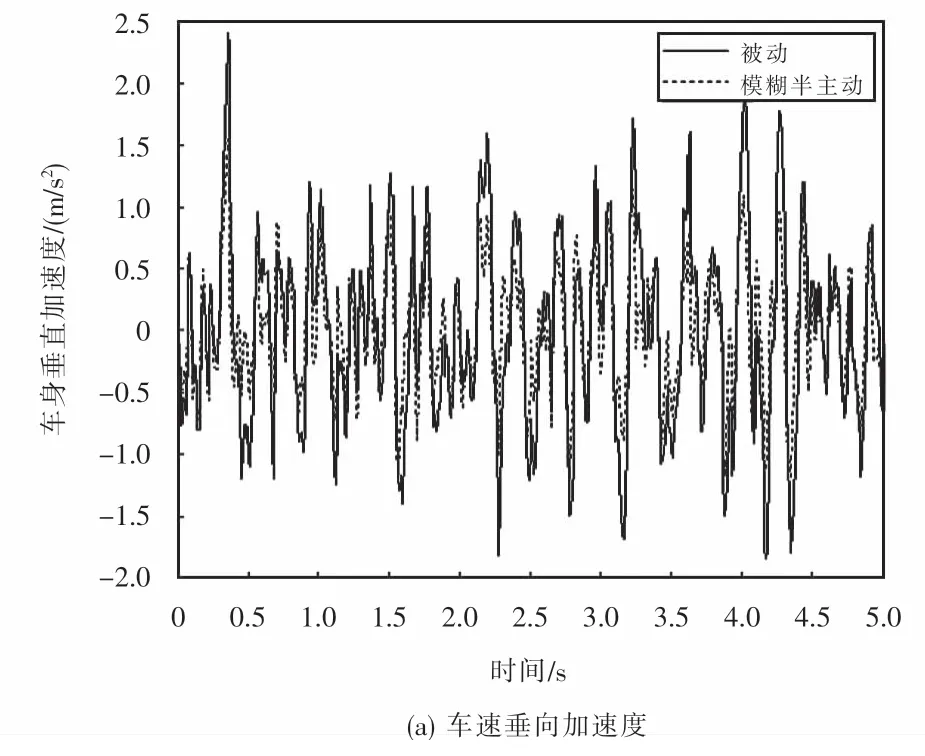
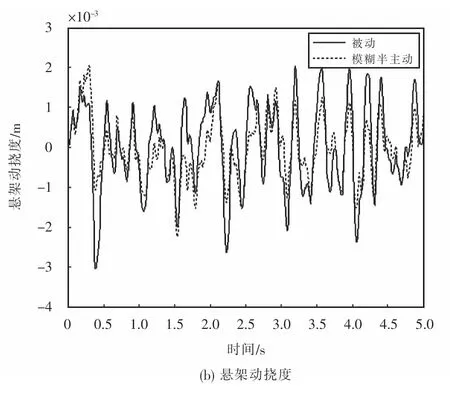
图8 随机路面激励下的车辆响应Fig.8 Vehicle response under random road excitation

5 结论

文章研究了阀控半主动减振器在模糊控制下的阻尼比跟踪特性.通过步进电机控制转阀的开度，可以实现很多种状态的阻尼，一方面可以实现阻尼比的大范围改变，另一方面降低了控制难度.通过建立控制系统的数学模型，经过模糊化运算，模糊推理和清晰化运算得出系统的脉冲传递函数.仿真分析的结果表明：阻尼比在0.35到0.45之间变化时，系统的控制效果快速稳定，加入传统的PID控制还可以有效地减小稳态误差.最后通过1/4车体模型进行验证，阀控半主动悬架的减振效果明显好于被动悬架.阀控半主动减振器模糊控制策略研究为车辆或者机械系统的减振设计提供了理论依据，特别是对机械系统的颤振衰减具有现实指导意义.