Ground-based/UAV-LiDAR data fusion for quantitative structure modeling and tree parameter retrieval in subtropical planted forest

Red Fekry,Wei Yo,b,＊,Lin Co,Xin Shen

a Department of Land Surveying and Geo-informatics,The Hong Kong Polytechnic University,Hung Hom,Hong Kong,China

b The Hong Kong Polytechnic University Shenzhen Research Institute,Shenzhen,China

c Co-Innovation Center for Sustainable Forestry,Nanjing Forestry University,Nanjing,210037,China

Keywords:Ground/aerial view mobile LiDAR Point cloud Co-registration Fusion QSM Tree parameter retrieval

A B S T R A C T Light detection and ranging(LiDAR)has contributed immensely to forest mapping and 3D tree modelling.From the perspective of data acquisition,the integration of LiDAR data from different platforms would enrich forest information at the tree and plot levels.This research develops a general framework to integrate ground-based and UAV-LiDAR(ULS)data to better estimate tree parameters based on quantitative structure modelling(QSM).This is accomplished in three sequential steps.First,the ground-based/ULS LiDAR data were co-registered based on the local density peaks of the clustered canopy.Next,redundancy and noise were removed for the ground-based/ULS LiDAR data fusion.Finally,tree modeling and biophysical parameter retrieval were based on QSM.Experiments were performed for Backpack/Handheld/UAV-based multi-platform mobile LiDAR data of a subtropical forest,including poplar and dawn redwood species.Generally,ground-based/ULS LiDAR data fusion outperforms ground-based LiDAR with respect to tree parameter estimation compared to field data.The fusion-derived tree height,tree volume,and crown volume significantly improved by up to 9.01%,5.28%,and 18.61%,respectively,in terms of rRMSE.By contrast,the diameter at breast height(DBH)is the parameter that has the least benefits from fusion,and rRMSE remains approximately the same,because stems are already well sampled from ground data.Additionally,particularly for dense forests,the fusion-derived tree parameters were improved compared to those derived from ground-based LiDAR.Ground-based LiDAR can potentially be used to estimate tree parameters in low-stand-density forests,whereby the improvement owing to fusion is not significant.

1.Introduction

Forest management is essential because of forest’s multiple roles,including water supply,mitigation of climate change,food production,and extraction of timber and fuelwood(FAO and UNEP,2020).Trees are one of the most important features of forests,and they change over time as they grow or degrade.Up-to-date information on trees and other forest elements is essential for a comprehensive interpretation of their ecological functions and processes.Light detection and ranging(LiDAR)systems obtain three-dimensional(3D)information with multi-functional details,showing their importance and popularity in forest mapping and management.Depending on the perspective of data acquisition,LiDAR systems can be divided into airborne and ground-based systems.The most widely used LiDAR system is the airborne laser scanning(ALS)system,which mainly features georeferenced data(Polewski and Yao,2019)to cover inaccessible forest areas with rough terrains or dangerous wildlife.The new generation of ALS utilizes unmanned aerial vehicles(UAVs)as a carrier platform for a laser scanner or simply an unmanned laser scanner(ULS).The ULS is a lightweight system that integrates a laser scanner with a global navigation satellite system/inertial measurement unit(GNSS/IMU)for positioning and orientation.By contrast,a common ground-based platform refers to a terrestrial laser scanner(TLS),which is normally able to provide a point cloud of higher density and more details compared to other LiDAR platforms.The main challenge with the TLS is occlusion effect,in which some distant areas are scanned with a low density or occluded by other objects within the field of view.The main solution to the occlusion problem is the TLS of the multi-scan mode,which functions by integrating two or more scans to reduce the occlusion effect in the resulting point cloud.These scans can be performed in either the static or kinematic mode,or both.

Recently,new advances in lightweight device development have facilitated the emergence of mobile LiDAR platforms such as backpack laser scanners(BLS)and handheld laser scanners(HLS),where the scanner is carried by a walking operator to acquire high-fidelity on-site point clouds in a kinematic manner.These advances enable the efficient and flexible scanning of impassable areas that cannot be reached by a vehicle(Oveland et al.,2018).In general,each LiDAR system group exhibits advantages and disadvantages with respect to the scanning results.Airborne systems scan to generate overhead observations,providing a high-density point cloud for the(high-level)tree canopy,whereas the lower level has a low-density point cloud.Conversely,ground-based platforms scan the forest while standing or moving on the ground,which in turn provides a higher level of detail for the under-canopy forest.Consequently,the viewing perspective significantly influences the quantity and quality of data obtained during point cloud acquisition.This implies that the integration of LiDAR point clouds from multiple platforms could contribute to a complementary interpretation of complex forest scenes by reducing occlusion effects and facilitating a more reliable estimation of tree parameters(Calders et al.,2015,2020).

The use of LiDAR in forests has largely automated the estimation of tree parameters,such as single stem diameter(Oveland et al.,2018;Pitk¨anen et al.,2019),tree height(Li et al.,2012;Corte et al.,2020;Hyypp¨a et al.,2020),leaf area index(LAI)and gap fraction(GF)(Stovall et al.,2017).These studies focused on retrieving specific tree parameters using individual LiDAR datasets,which were selected based on the target parameter.However,a complete tree model is more comprehensive and informative;thus,it is desirable.Quantitative structure modelling(QSM)of trees aims to build a comprehensive tree model in which all associated tree parameters can be accurately estimated.The basic idea of QSM is to model different tree segments with geometric primitives,with cylinders being the most commonly used.Geometric primitives are combined to form a complete tree model,involving the basic elements of tree structures,such as stems,branches,and foliage(Raumonen et al.,2013).The aboveground biomass(AGB)of a tree depends mainly on its stems and branches,and tree trunks can be measured directly in the field,although this is difficult for branches(Stovall et al.,2017).Nevertheless,branches can be modeled using the QSM of individual trees with their derived attributes,which include the order,diameter,and length/area/volume of each branch element.

Tree parameters can be further enriched by applying the QSM approach to ground/aerial view-fused LiDAR point clouds.This is because of the complementarity of point clouds acquired from different perspectives,particularly the combination of ground-based and airborne platforms.Challenges in using fusion results from ground-based and airborne LiDAR point clouds for QSM-based tree reconstruction include data redundancy,noisy/outlier points,and misregistration effects because most tree parameters must be determined with centimeter-level accuracy.Therefore,it is desirable to deploy a comprehensive tree model derived from the fusion of ground-based and airborne LiDAR data to overcome such challenges.

In this paper,we present a general framework for QSM-based tree reconstruction from the fusion of ground-based and ULS LiDAR data and assess the retrieved tree parameters that particularly benefit from this fusion.This framework is accomplished in three stages:co-registration of ground-based and ULS LiDAR data,fusion of ground-based and ULS LiDAR data,and investigation of tree parameter retrieval from fused data using QSM.

The main contributions of this study are as follows.

⋅Identification of co-registration virtual keypoints based on the detection of local density peaks of the clustered canopy.

⋅Fusion of ground-based and ULS LiDAR point clouds based on the removal of redundancy and noise.

⋅Investigation of the impact of fused ground/aerial-view LiDAR point clouds on the estimation of tree parameters based on QSM.

The rest of this article is organized as follows:Section 2 describes the literature review on the co-registration of point clouds in forests and the reconstruction of trees from point clouds.Section 3 presents the materials used in this research,including the study area,forest plot descriptions,and data collection.The detailed research methodology of this study is presented in Section 4,and Section 5 describes the experimental design and evaluation scheme.Section 6 presents the results and their interpretations for both point cloud co-registration and tree parameter estimation.Finally,Section 7 presents the conclusions,limitations,and outlook of this research.

2.Related works

The co-registration of point clouds in forested areas is widely reported in the literature.Kelbe et al.(2016)performed marker-free TLS point cloud co-registration by generating view-invariant feature descriptors and applying a voting method to determine the optimal transformation parameter.Paris et al.(2017)completed ALS-TLS point cloud fusion for tree canopy structure assessment by maximizing normalized cross-correlation between a canopy height model from ALS and a corresponding model from TLS using a planar Euclidean transformation.Similarly,Polewski et al.(2016)deployed planimetric and vertical distances between tree locations within the same forest plot to build a similarity function for finding the corresponding trees.Subsequently,two-dimensional(2D)rigid transformation parameters were obtained after a heuristic search over the correspondences.Moreover,Polewski et al.(2019)updated the similarity function and used a simulated annealing algorithm to find a 3D rigid transformation between tree locations from BLS/UAV point clouds.In addition,a triangulated irregular network of tree locations was created to find the corresponding triangles for the fusion of BLS,UAV,and multi-scan TLS point clouds in dawn redwood forest plots(Guan et al.,2019).These methods rely on tree locations to perform co-registration,which is challenging in windy forests and(sub-)tropical forests with high stand density and canopy closureness.Dai et al.(2019)performed co-registration of ALS/TLS point clouds by analyzing common crowns to detect the local maximum of the probability density function.This method utilized coherent point drift to perform a rigid 3D transformation between point clouds.In our study,co-registration was performed using virtual keypoints defined for clusters of forest canopies,without requiring tree segmentation and localization.Furthermore,none of these studies used their co-registration/fusion results for further forest analyses,such as tree parameter estimation,although both ground-based and airborne LiDAR systems have been used for 3D forest mapping(Ye et al.,2019;Calders et al.,2020;Navarro et al.,2020).

In addition,quantitative structural modelling of trees using imagebased/LiDAR point clouds has attracted much interest in recent years.Based on the information obtained from point clouds using available LiDAR platforms,several studies for different purposes have been conducted.From a dataset point of view,static TLS is a common platform,because it guarantees high density and low occlusion by integrating multiple scans of the same scene.However,its limitations include multiscan misregistration,occlusion in single-scan mode,and canopy with sparse point sampling.A wide range of TLS applications in tree reconstruction includes stem curve determination(Wan et al.,2019),branch architecture quantification(Lau et al.,2018),forest inventory parameter derivation(Kalwar et al.,2021),and quantitative structure modeling and biomass estimation(Calders et al.,2015).These studies found that deriving tree heights from TLS data is relatively unreliable.Although TLS can quantify both diameter at breast height(DBH)and tree height,its performance in dense forests still needs to be improved.Hence,the main challenges in applying TLS to forest parameter estimation are associated with occlusion effects and local forest conditions.TLS point clouds have also been used to evaluate the extraction of apple tree branch information from BLS point clouds(Zhang et al.,2020),where only low trees with heights of 3–5 m have been reported to be well modeled by BLS.Ko et al.(2021)reported that BLS estimated the subtropical tree height with lower accuracy than DBH because of the local forest conditions such as stand density and stem width.Furthermore,the use of point clouds from airborne platforms such as ALS and UAVs has been investigated to determine their suitability for creating tree QSMs.For instance,Hu et al.(2017)has reported tree modelling from ALS data to complement the incomplete point cloud by simulating trunk points based on bounding boxes of tree and ground points.Yao et al.(2012)also reported that only up to 30%of tree stem points in a temperate forest could be captured by airborne waveform LiDAR.Additionally,Liang et al.(2019)found that the stem attributes,including DBH and stem curve,have not yet reached the accuracy level of ground-based LiDAR systems,despite the tree heights with high accuracy provided by ULS.Wang et al.(2019)concluded that ULS-derived AGB is unreliable because of limited access to DBH for ULS and smaller trees in dense boreal forest.

Another study(Navarro et al.,2020)used a UAV point cloud for AGB estimation of mangrove trees;however,the understory and young trees could not be detected by UAV.Moreover,a comparison of the ULS and TLS point clouds was conducted as inputs toTreeQSM(Brede et al.,2019).It was concluded that the tree volume was underestimated for dense forest stands from the ULS data due to sparse trunk points.In addition,Shimizu et al.(2022)estimated tree parameters from TLS/UAV-photogrammetry data fusion and reported a remarkable improvement in tree height.Furthermore,Terryn et al.(2022)evaluated the tree parameters derived from the TLS and ULS data against their fusion results which are deemed as a benchmark.They reported that both TLS and ULS-derived parameters were comparable to those of their counterparts from fusion.

Therefore,a combination of point clouds from multiple platforms has not yet been investigated and applied to tree reconstruction based on QSM,although such data integration is expected to enhance forest interpretation and tree parameter estimation.According to the reviewed studies and to the best of our knowledge,the fusion of ground-and aerialview LiDAR point clouds has not yet been deployed and investigated for QSM based tree parameter retrieval.

3.Materials

3.1.Study site

The study area included seven sample plots in the subtropical forest of Dongtai(120.8263°E,32.8735°N)in southeastern China.The sample plots contained two tree species:poplar(deciduous)and dawn redwood(coniferous).The sample plots were selected according to GIS-based forest inventory data to cover different forest parameters including tree species,growing stage,and forest structure(e.g.stand density,DBH,and tree height).The ULS sample plots were circles with a 50-m diameter.The sample plots of backpack laser scanner(BLS)and handheld laser scanner(HLS)were squares(30 m×30 m)to reduce the effect of the alignment errors of the measurements and accuracy degradation during the mobile LiDAR data collection in the final point cloud.The location and distribution of the sample plots within the study area are shown in Fig.1,and the forest parameters of the sample plots are listed in Table 1.The study area is a planted forest;therefore,the terrain was near-flat without sharp slopes.In addition,the undergrowth structure of the poplar plots(1,2,4,and 5)was simple with few and low shrubs.In contrast,there were a large amount of irrigated grass and shrubs in dawn redwood plots(3,6,and 7).

Table 1Forest parameters of the sample plots.

3.2.Data collection

3.2.1.Field data

Field measurements of DBH,tree height,crown base height(CBH),and crown widths(CWs)in the east-west and north-south directions were taken for 98 individual trees in the seven plots.Fig.2 shows the distribution of DBH and tree height measurements of the poplar dawn redwood species.

3.2.2.ULS data

Fig.1.Study area and location of sample plots.Inset shows the location of Dongtai forest in China.(a)Location of the study site in the forest(red rectangle).(b)Distribution of the sample plots(green circles)in the study area.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

The point cloud of the ULS was acquired using the GreenValley UAV LiDAR platform.The system consisted of a Velodyne Puck VLP-16 laser sensor,Novatel GNSS receiver,Novatel SPAN-MEMS-IMU,and microcomputer,as shown in Fig.3a.The flight altitude was 86 m,at a speed of 3.6 m⋅sec-1.The sensor parameters are listed in Table 2.An example of a ULS point cloud is shown in Fig.4d.

3.2.3.Ground-based LiDAR data

Ground-based LiDAR point clouds were acquired using three platforms:a single-head backpack laser scanner(SBLS),dual-head backpack laser scanner(DBLS),and HLS.The GreenValley BLS system consists of three main parts:a Velodyne Puck VLP-16 scanner,a position and orientation system(POS),and a touch pad for data collection control.The point cloud was generated using the simultaneous localization and mapping(SLAM)technique,which integrates the scanning data and POS information.SBLS data were collected when the single scanner head was mounted horizontally,whereas dual-head mode data were acquired with two scanning heads co-aligned in both horizontal and vertical directions.The ZEB-REVO HLS system was used for point cloud data collection,which consisted of a 2D laser scanner rigidly coupled to an IMU installed on a motor drive.The 3D information was generated by the third dimension provided by the scanning head motion of the motor drive.The 2D scanning data were combined with IMU information for 3D point cloud generation based on SLAM.The typical scan range was 15–20 m outdoors with 270°×360°fields of view in the vertical and horizontal directions.The system operation in forest mapping is shown in Fig.3c.

The configuration of the different platforms,as listed in Table 2,influenced the data collection in terms of point density and information details.Fig.4 shows a poplar-plot example of point clouds collected from the four systems.In Fig.4a and b,only trunks are acquired in the case of HLS and SBLS.By contrast,the DBLS point cloud provided more information about tree structure at low and relatively high forest levels.It is worth noting that the ground-based dataset is preliminarily aligned to the UAV-LiDAR georeferenced coordinate frame using artificial markers.Coarse alignment resulted in an inaccuracy of greater than 2 m.

Table 2LiDAR sensor parameters for multiple systems.

4.Methodology

The proposed workflow aimed at performing quantitative structural modelling of trees using ground-based/ULS LiDAR data fusion.This goal was achieved in three leading phases,as illustrated in Fig.5.Phase I:Markerless co-registration of point clouds;Phase II:point cloud fusion;Phase III:QSM of trees.The detailed steps of these three phases are explained in the following subsections.

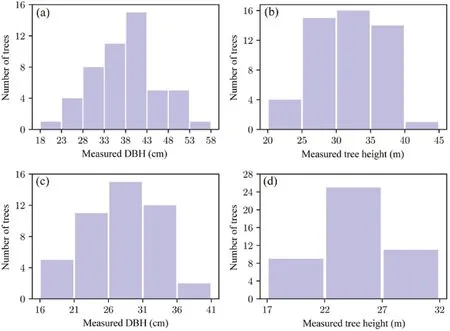
Fig.2.Histograms of DBH and tree height from field measurements.Top row:poplar species.Bottom row:dawn redwood trees.

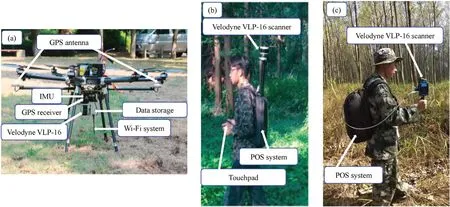
Fig.3.Different LiDAR systems used for data collection in this study.(a)UAV-LiDAR with its main components;(b)BLS with its system components;(c)main components of HLS.

4.1.Markerless point cloud co-registration

The developed co-registration pipeline,an adaptation of the work of Fekry et al.(2021),was proposed to perform ground/ULS point cloud co-registration.This method developed and implemented an approach to ULS strip alignment in plantation forests by analyzing the topological persistence of point clusters from the forest canopy so as to determine the most stable local maximum.

Depending on the viewing perspective of the LiDAR platform,the local height maxima of the corresponding clusters from the ULS point cloud were nearly identical.Different results were obtained when using data from different perspectives,such as airborne and ground-based LiDAR platforms.The definition of keypoints in Fekry et al.(2021)was replaced by searching for the local density peak of each cluster,rather than topological persistence.The definition of keypoints in the co-registration pipeline allowed the co-registration of ground/ULS point clouds without the need for additional information about the parameters of the tree stand.The definition of the keypoints is described in the following subsection.

4.1.1.Keypoints extraction

Point cloud registration aims to integrate datasets from two or more data-collection platforms,most of which have different perspectives or individual data characteristics.Therefore,defining the appropriate keypoints for co-registration is challenging,particularly when working with forest point clouds with few objects.Moreover,the problem becomes even more complicated in plantation forests,where trees cannot be characterized by species,age,height,stem diameter,etc.,because the tree-related parameters are nearly the same at the plot level.Therefore,the scanned canopy was used as a common feature in both the datasets.The canopy was partitioned into point clusters using a hierarchical density-based algorithm(HDBSCAN)(Campello et al.,2013),which requires only one input parameter(MinClusterSize).This algorithm has some special advantages:it learns clusters of arbitrary shapes,marks low-density points as noise,and operates with data of different densities.In this study,clustering was an intermediate step and was not aimed at segmenting individual trees,which meant that a single cluster was not a single crown.The number of clusters from both datasets was not identical,and the ULS point clouds yielded larger ones because the ground-based datasets were subsets of the ULS plots.

A point cloud PC∊R3was partitioned into a set of clusters,Ck={C1,C2,C3,…,Cn},k∊1:n.We assumed that each single clusterCkcontaining any number of points provides a single keypoint.For each pointPi∊Ck,two components were computed:the local density ρi,which is the number of points within a distancedcfrom pointi,and its distance δifrom higher-density points,which is the minimum distance between the point and other higher-density points.Therefore,ρiand δidepend on the distancesdijbetween the cluster data points.The two components were compared at high-density points,and the 2D position of the keypoint ofCkwas defined as theXYcoordinates of the density peak that received the largest δ and highest ρ.A complete 3D keypoint was identified by projecting the extracted local density peak onto the digital elevation model(DEM)of each dataset.This step was required to align the point clouds in the horizontal and vertical directions simultaneously.

wheredijis the Euclidean distance of a pointifrom the higher-density points in neighborhood,dcis the cutoff distance.

A set of keypoints forCkclusters was generated.Thus,two sets of keypoints were formed:one referred to the point cloud from the groundbased LiDAR(source),whereas the other represented the ULS point cloud(target).The main advantage of this criterion for the extraction of keypoints is that it can mitigate the limitations of tree localization,particularly when integrating point clouds influenced by environmental factors,such as wind,or subject to scene incompleteness acquired from different perspectives.For example,Fig.6 shows two examples of extracted keypoints that are independent of the stem or its center.The full keypoints(red dots)are defined by projecting the extracted peak density points onto a DEM of the point cloud to obtain their heights.Case I in Fig.6 shows that the stem center and projection of the treetop do not coincide even though the tree is vertical.Case II shows the effect of the tree being skewed owing to its growth or environmental factors,resulting in the same situation as in Case I.

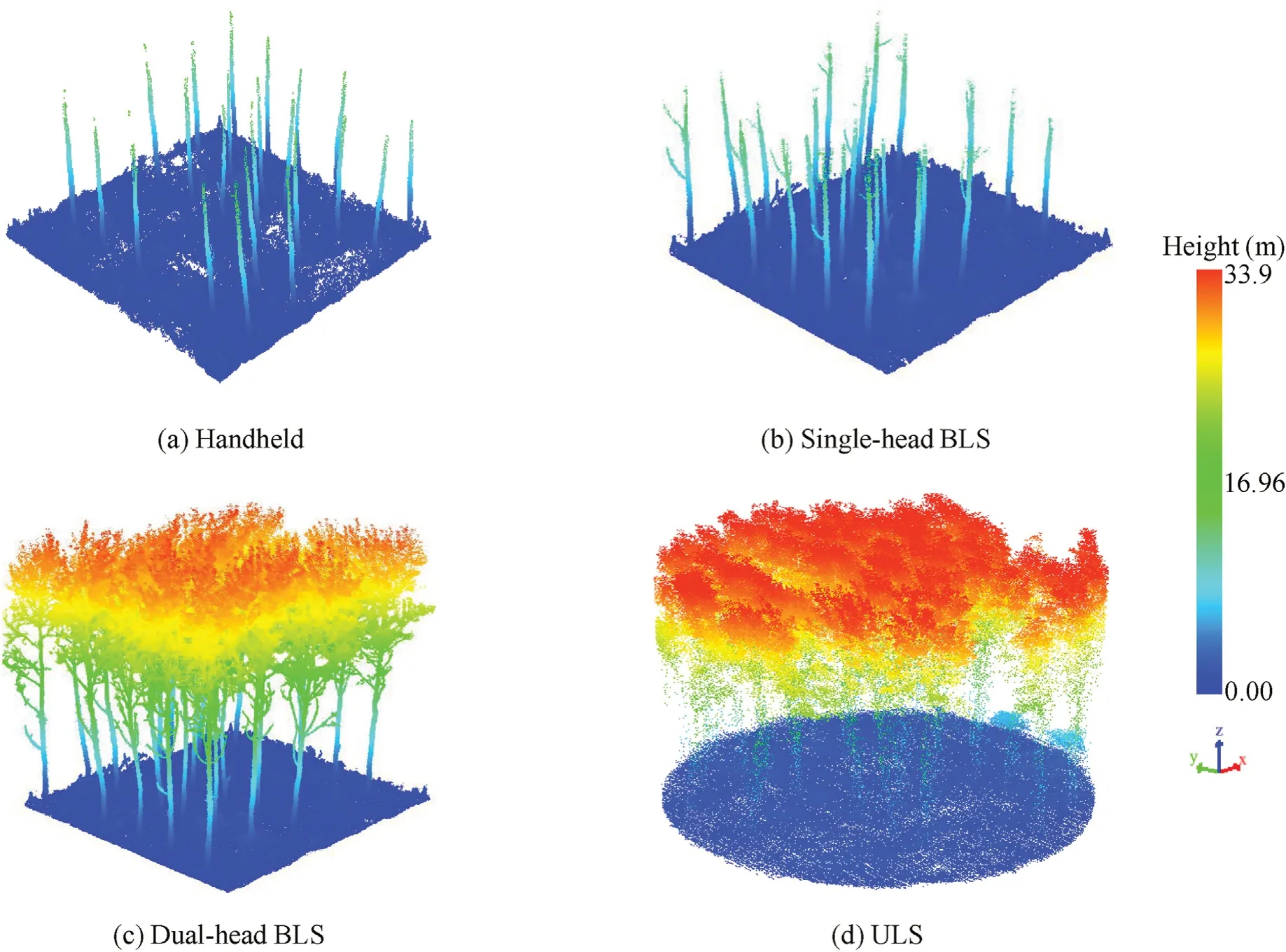
Fig.4.Point clouds from the four LiDAR platforms for a poplar plot.The influence of the scanning perspective is reflected in the information obtained.(a)HLS data;(b)single-head BLS data;(c)dual-head BLS data;and(d)ULS data.

Fig.5.Research workflow.

Fig.6.Extraction of keypoints from the ground-based and ULS datasets.Blue points:extracted points based on density peaks.Red points:full keypoints after projection of the point cloud onto DEM.Dashed lines indicate the non-coincidence between the treetop and stem center.Case I:the stem center and projection of the treetop are not identical even though the tree is vertical.Case II:effect of the tree being skewed owing to its growth or environmental factors.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

4.1.2.Feature matching and transformation

Following the extraction of keypoints,the feature matching and transformation procedure of Fekry et al.(2021)was applied to co-register the ground-based and ULS point clouds.Feature descriptors were formed based on the distance and bearing angle of each point to the centroid of the point set.Subsequently,one-to-one correspondence was determined by graph matching.Finally,three-dimensional rigid-body transformation parameters with six DoF(three rotationsRZ,RY,RX,and three translationsTX,TY,TZ)between the source XSand target XTkeypoints sets were calculated,as shown in Equation(3).Fig.7 shows the keypoints from the ground-based point cloud and the ULS before and after co-registration.

where R is the rotation matrix,and TXYZis the translation vector inX,Y,andZ,respectively.

There were still some discrepancies between the co-registered point clouds,which posed a challenge for tree parameter estimation because they should be computed at the centimeter level.Therefore,the distance between point cloud pairs should to be further minimized.The most common fine-registration algorithm is the iterative closest point(ICP),which finds a rigid transformation to align the source point cloud with the target cloud.Fig.8 shows an example of the effect of the ICP refinement on the final co-registration results.The focus is on overlapping crowns,where the green points belong to the ULS cloud,and the ground-based dataset is shown in red.It can be observed that the toplevel benefits strongly from ICP,whereas the lower-levels contain fewer points from the ULS.

4.2.Point cloud fusion

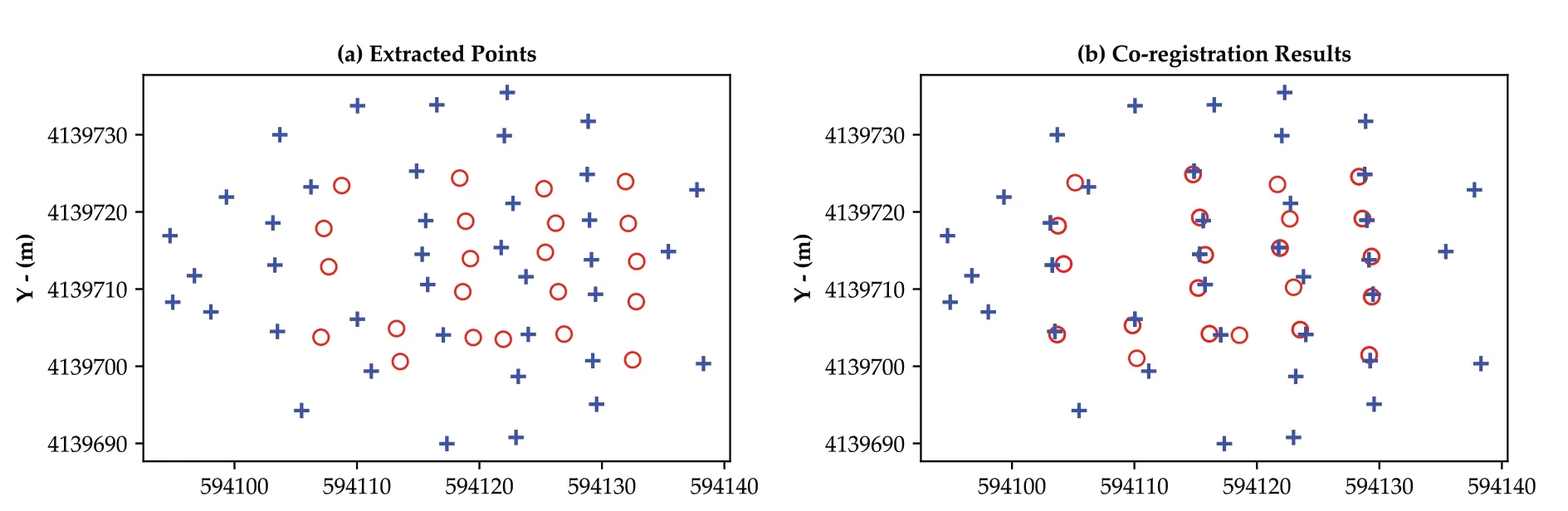
Fig.7.Transformation of keypoints by permutations.Red circles:source keypoints(ground-based LiDAR).Blue crosses:target keypoints(ULS dataset).(a)Before coregistration,and(b)Co-registered keypoints.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

Fig.8.Profile along a poplar plot showing the refinement of co-registration results according to ICP.An example result shows the minimization of discrepancies between ground-based(red)and ULS point clouds(green).(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

The main goal of fusion is to integrate two or more registered point clouds to create a new dataset that leverages each one.The level of detail(LoD)of ground based and ULS LiDAR point clouds is different.For example,the ULS point density varied spatially and was relatively lower than the point cloud density of the ground-based LiDAR platforms.However,the ULS point cloud enabled terrain reconstruction and surface modelling despite the lack of points under the canopy and near the ground.By contrast,the ground-based dataset was derived from two mobile LiDAR devices that provided a high point density at lower levels.This resulted in a detailed representation of the tree trunks and branches,whereas the point density was limited to higher levels of the tree canopy.Fusion targets common objects that are mostly exclusively present in the upper forest layers in the case of ground-based and ULS LiDAR data fusion.This feature difference in the point cloud may lead to conflicts as some points are redundant,whereas others are considered as noise or outliers.Fig.9 shows an example of co-registered point clouds of a poplar tree,where scattered points surrounding its stem are noise,and its top contains complementary points.The redundant points increase the computational cost by posing potential conflicts in the structure,whereas noisy points can severely affect tree modelling,particularly cylinder fitting.Therefore,noisy points were prioritized during the removal process.The detailed steps for removing noise and redundancy are as follows:

4.2.1.Elimination of redundancy

The co-registered point clouds included data from two perspectives.Therefore,there were a large number of undesirable points in the overlapping areas,which were classified as noise and redundant.The noisy points are mainly represented by the scattered points around the stems,as shown in Fig.11a,most of which emanate from the ULS point cloud.However,the redundant points were captured by both datasets and eliminating them did not affect the quality of the point cloud.Redundant points were first detected and removed to reduce the computational cost and alleviate potential conflicts in the structure.

The scattered point cloudPCcontained a set of points in R3.It was partitioned into small cubes of side lengthl.For each pointpi,the distances to all points within the cube were computed.All points whose distances topiwere smaller than a threshold ε were considered redundant and were therefore eliminated.In the case of ground-based and airborne LiDAR data fusion,the crowns have the most overlap,and redundant points are nearly always present.Thus,the redundancy elimination was performed on the fused point cloud to preserve only the most important information.Fig.10 shows the results of redundancy removal from the fused point cloud,with the higher tree levels magnified to show how they appear after redundancy removal.Redundant points come from ULS dataset with sparse points on tree trunks and branches.Under-canopy levels still contain scattered points around the trunks and branches,which are problematic for the modelling algorithm.Therefore,these points were considered noise and removed based on statistical filtering of the point cloud.

4.2.2.Removal of noise

A statistical method(Ning et al.,2018)was used to remove noisy points by computing the distribution of distances between points and their neighbors in the dataset.Considering a Gaussian distribution with its mean and standard deviation,the neighbor points with mean distances outside the interval defined by the mean and standard deviation of the global distances were considered as noise and were therefore removed from the dataset.

The scattered point cloudPCcontains a set of points in R3.For each pointpi∊PC,the local neighborhoodpnbrwithin a fixed radius ν is determined for each pointpi∊PC.The mean distanceDifrompito its neighborskinpnbris computed as follows:

whereEDis the Euclidean distance betweenpiand its neighborj∊pnbr.The Gaussian distribution GD(pi)forpnbrinpiis represented as follows:

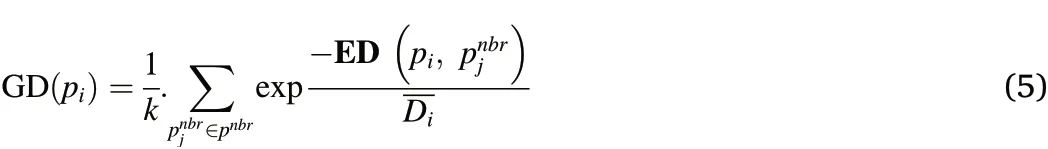
The probability of consideringpias a noisy point is computed using GD(pi),as expressed in Equation(6),where σ is the probability threshold.

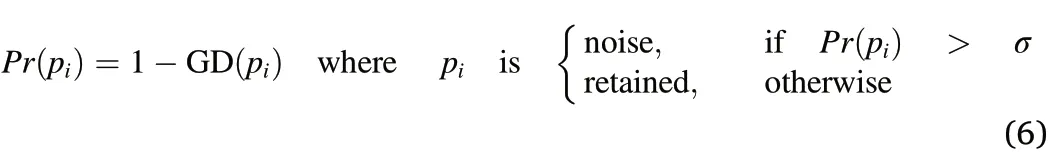
Fig.9.Co-registered point clouds with the different types of conflict points.(a)Co-registered point cloud of a tree,and(b)different types of points within overlapping regions.Redundant points from ULS(green color)existed particularly at the high-tree levels on the trunk and canopy.Noisy points were scattered around the stem and branches at the low-tree levels.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

Noisy points are shown in the vicinity of the stems from the ULS point cloud,as highlighted by the red rectangles in Fig.11.Moreover,redundant points are mainly found in the crown region,which has the largest overlap between the two datasets.

4.3.Tree modelling

4.3.1.Individual tree segmentation

Tree segmentation is essential for reconstruction.If it is performed accurately,the structural attributes of the tree can be estimated,including the DBH,height,basal area,and wood volume.Various tree segmentation approaches have been developed.In this study,individual trees were accurately segmented in three steps(Tao et al.,2015):normalization of the point cloud,stem detection and estimation of DBH,and segmentation of the crown.A DEM was generated from the point cloud using ordinary kriging(Guo et al.,2010),and the point cloud was normalized by subtracting the heights of the DEM from the heights of the point cloud.

4.3.2.Leaf-wood separation

Reconstruction of trees from the point cloud mainly focused on the woody part because the leaves and foliage did not have a uniform distribution,which might affect the final modeling results.The classification of forest point clouds into woody and foliage clouds has been studied from different perspectives.Based on the classification features,the developed methods can be categorized as geometric(Wang et al.,2018;Moorthy et al.,2020),radiometric(B′eland et al.,2013)or both(Xu et al.,2021).In this study,the method of Moorthy et al.(2020)was adopted for classification purpose.The main advantage of this classification method is that it can function with point clouds of varying densities by exploiting multi-scale features.

The algorithm was employed to classify forest point clouds by combining the geometric features of the normalized eigenvalues and the zenith angle of the eigenvectors of each point at multiple spatial scales.The eigenvalues λ0,λ1,and λ2represent the distribution of points within the neighborhood,where the local neighborhood of each point is defined by setting a sphere of radius μ={μ1,μ2,μ3,…,μn}.The eigenvectors and eigenvalues were obtained by first computing the covariance matrix of the local neighborhood of each point following the procedure in Belton et al.(2013)according to Equation(7).

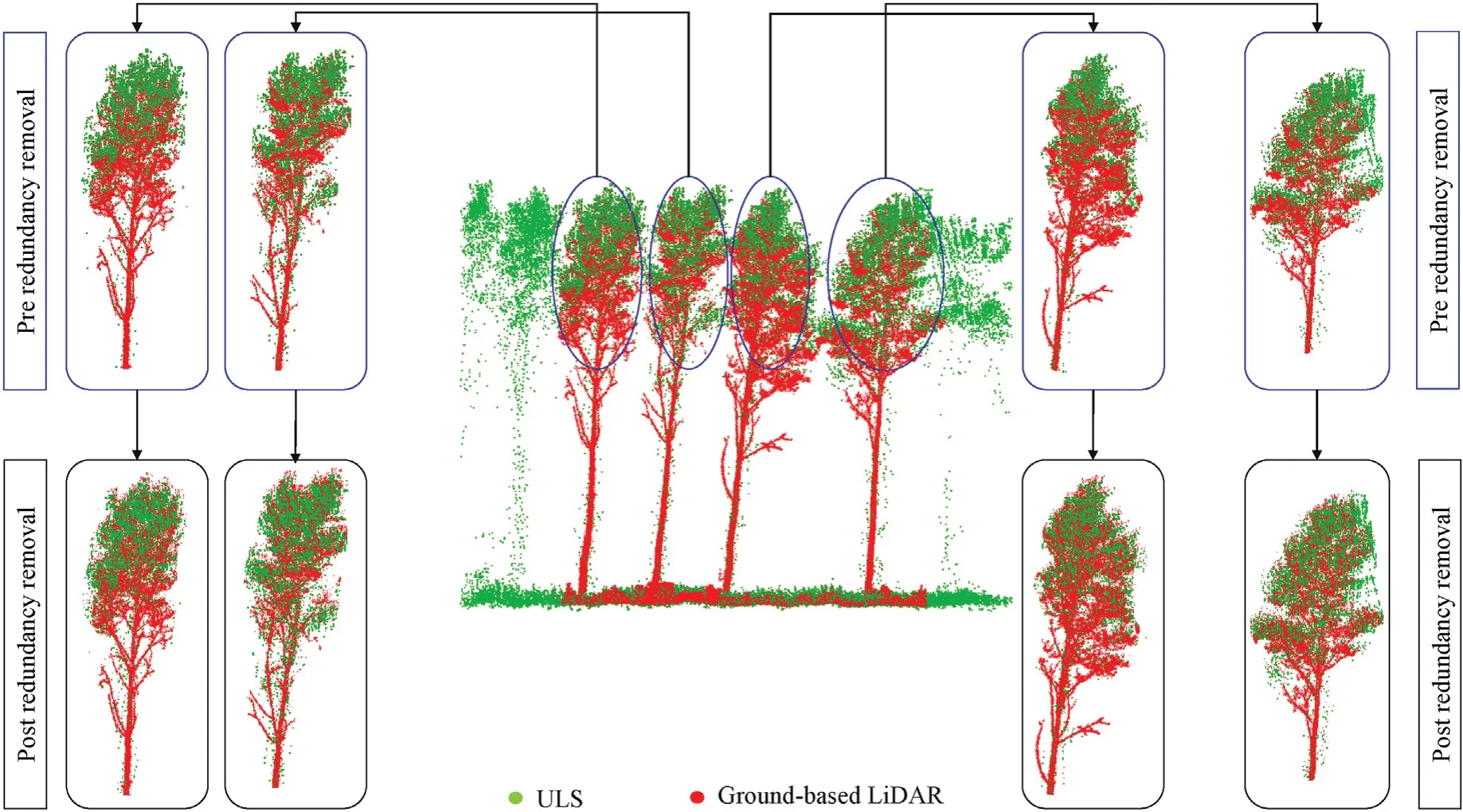
Fig.10.Profile along a poplar plot showing the removal of redundant points.An example result shows the removal of duplicate points in the co-registered point clouds.The ground based and ULS datasets are shown in red and green,respectively.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

wherepiis theithpoint ofnpoints in the neighborhood,andpis the mean of the neighborhood coordinates.Then,the eigenvalues were obtained by decomposing Σ3×3using Equation(8).The eigenvalues were normalized to the range[0,1]by dividing each eigenvalue by the sum of λ0,λ1and λ2.where λiis the eigenvalue in a directioniwithin the neighborhood,andeiis the unit vector in directioni.On a spatial scale μ∊{μ1,μ2,μ3,…,μn},let the normalized eigenvalues at μ be λ1,λ2,λ3such that λ1>λ2>λ3and their corresponding zenith angles of the eigenvectors are θ1,θ2,and θ3.The computation of such features at each point was used to capture the distributions of different tree segments such as the trunk,branches,and leaves on a local spatial scale.The first eigenvalue λ1of the trunk and branches was greater than λ2and λ3,and the zenith angle of the trunk was always near 0°or 180°,whereas this was not the case for leaves and branches.Therefore,woody and leafy points can be distinguished based on the differences in their distributions.An example of this result is shown in Fig.12,where the poplar species are shown in the top row and the dawn redwood species in the bottom row.The left column shows the raw point cloud,and the right column shows only the woody parts of the point clouds of the two example plots.

4.3.3.Tree parameter estimation

A variety of algorithms have been used to perform tree modeling based on QSM,includingTreeQSM(Raumonen et al.,2013),SimpleTree(Hackenberg et al.,2015),andPypeTree(Delagrange et al.,2014).TreeQSMis mostly used for tree reconstruction and the experiments involving destructive methods show that it can achieve high accuracy in parameter estimation.Although the model should be continuously improved in terms of parameter optimization and visualization,the geometric topology of the tree branches is an impediment.TheSimpleTreealgorithm is relatively complicated because it requires the branch diameter as the input and does not construct a branch cylinder to recover its geometry.By contrast,PypeTreeonly provides a general description of the topological structure of a tree without reconstructing the branches.

In this study,the algorithmTreeQSMwas used to reconstruct the trees based on QSM.The algorithm covered the tree point cloud with small contiguous patches and used a building-brick approach to create a tree surface from these patches.Cylinders of different sizes were used to approximate the trunks and branches.Small cylindrical patches were used to reconstruct the tree segments in the two main phases.In the first phase,the coarse structure of the tree was identified using large patches of constant size with a radius(Patch Diameter1)that crossed the tree.In the second phase,a fine cover set ranging from Patch Diameter2(min)to Patch Diameter2(max)was used to obtain branches.The individual branches were then reconstructed using the least squares of the connected cylinders.

One of the important considerations inTreeQSMis the Patch Diameter2(min)setting,as it determines the extent to which the smallest branch element can be reconstructed,and thus the level of detail recovered from the data.Finally,the tree segments were geometrically reconstructed:the trunk was reconstructed from the base of the tree to its top using the neighborhood of the cover sets that had been enlarged to form the trunks.For more information onTreeQSM,see Calders et al.(2015),Gonzalez de Tanago et al.(2018),and Raumonen et al.(2013).An example of tree modeling based onTreeQSMis shown in Fig.13.

5.Experimental design

5.1.Parameter setup

The main parameters utilized for point cloud co-registration were the minimum number of points required to form a cluster in HDBSCAN,which was derived from the point cloud density,and the distance threshold,Dthr=1 m.The inputs of the algorithmTreeQSMwere PatchDim1=[0.06,0.09],PatchDim2Min=[0.0364,0.0674],and PatchDim2Max=[0.0485,0.09].The DEM was created at a resolution of 0.5 m.

5.2.Evaluation scheme

5.2.1.Co-registration

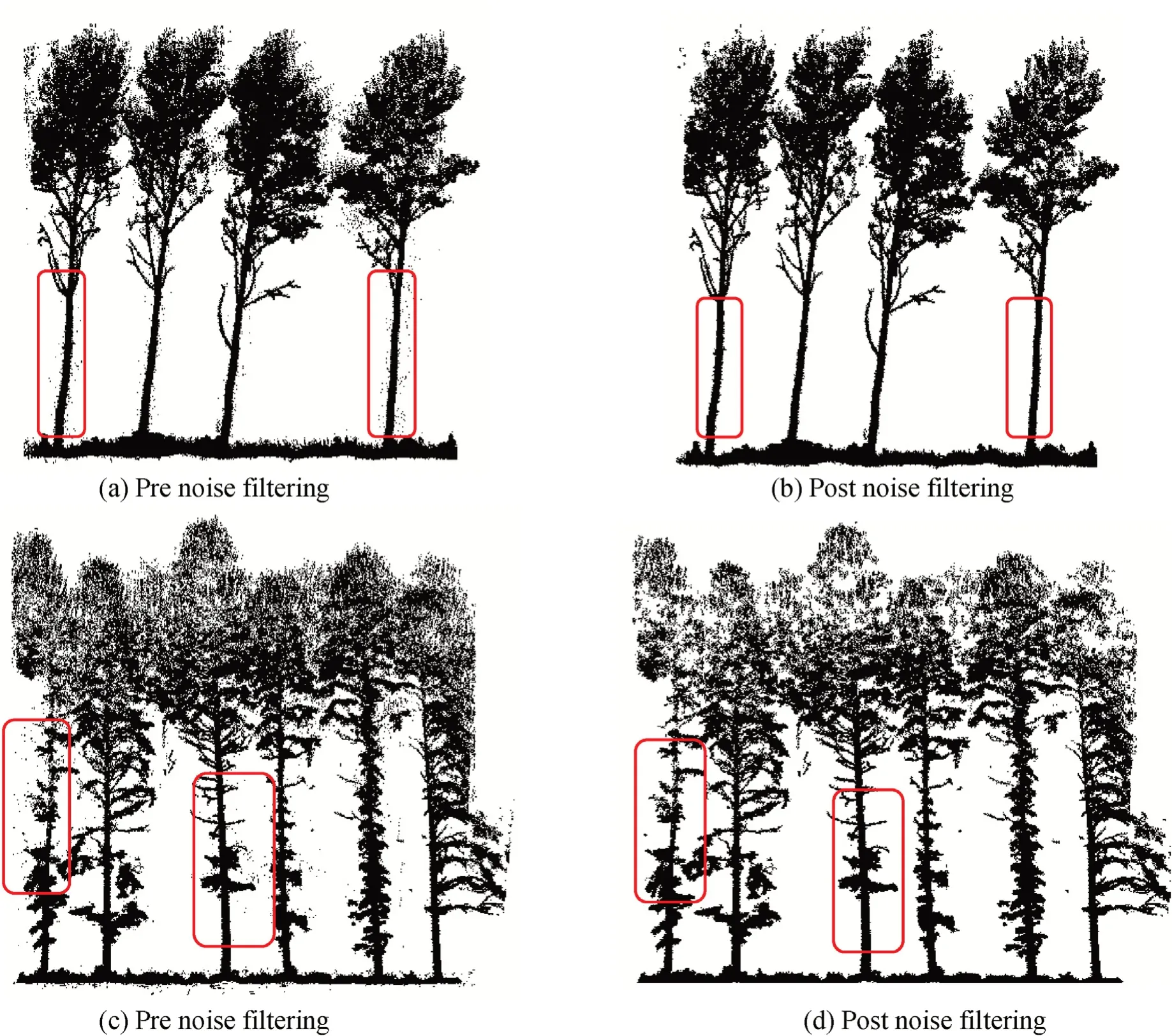
Fig.11.Profiles along the point clouds showing the effects of removal of noise and redundant points from the ground-based/ULS fusion results.(a)and(b)one case of poplar plot,(c)and(d)one case from a dawn redwood plot.

The co-registration results were evaluated by calculating the distance residuals between the matched keypoints from the ground-based and the ULS point clouds.Accordingly,the Euclidean distances between the matched keypoints were calculated after the co-registration.Let xiand xjbe the 3D coordinates of the matched keypoint pair,i∊XSsource keypoints andj∊XTtarget keypoints,respectively.Let the Euclidean distance between the two points EDij=‖xi-xj‖.The smaller the EDij,the higher the accuracy of co-registration.Additionally,the matching per-

centage was calculated for all plots as

5.2.2.Tree parameter estimation

The tree parameters obtained by modeling the corresponding individual trees(poplar and dawn redwood species)based on the groundbased dataset and ground-based/ULS LiDAR data fusion were compared to their corresponding field measurements.DBH,tree height,tree volume,crown area,and crown volume were evaluated based on the reference field measurements.The evaluation was performed in terms of the coefficient of determination,R2,root-mean-square error,RMSE,and relative root-mean-square error,rRMSE.

Because field measurements were not performed directly for tree volume(V),crown area(CA),and crown volume(CV),they were calculated based on the field measurements of DBH,tree height,CBH,and CWs.In this study,theVof poplar and dawn redwood tree species was calculated using models from Gao et al.(2021)because they were developed for similar forest types and tree species.The standard volume was computed based on the correlation between tree height and DBH as stated in Equation(9).

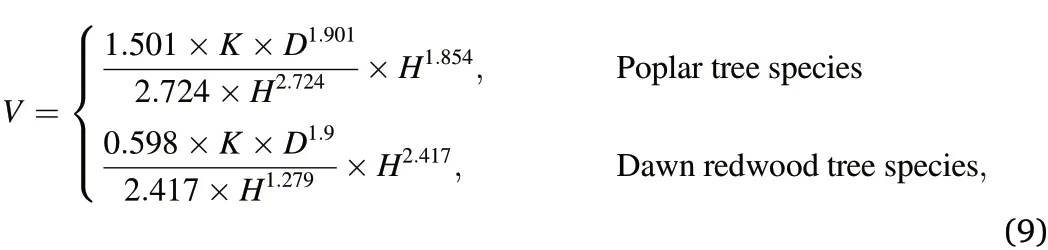
whereHandDrepresent the tree height and DBH,respectively,whileKis a constantMoreover,the field measurements of CBH and CWs were used to generate the ground truth for the CA and CV based on the geometric simulation.The CA was calculated as the oval area of the

6.Results and discussion

6.1.Markerless co-registration of point clouds

Fig.12.Classification of point cloud into wood and leaves.(a)and(b)one case of poplar plot,(c)and(d)one case of dawn redwood plot.Point clouds are colored with respect to height and the woody parts are represented in brown.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

Ground-based LiDAR point clouds were successfully co-registered with ULS point clouds in all sample plots.The distance residuals at the matched keypoints from ground-based and ULS data of each plot are calculated according to the criteria in Section 5.2.1.Fig.14 shows the distribution of these distance residuals of each plot,where the red lines represent the medians of the distance residuals in each plot.The residuals in each plot were divided into four parts,such that each part contained 25% of the residuals,and the rectangular part represented the interquartile range and contained 50%of the data.The interquartile ranges of the poplar plots(1,4,and 7)varied from 30 to 60 cm,except for plot 6,which ranged from 30 to 50 cm.However,the dawn redwood plots(2 and 3)had larger interquartile ranges of 40–70 cm,with the exception of plot 5,which ranged from 40 to 55 cm.

In general,the lower mean distance residuals of poplar plots 1,4,6,and 7 were lower than those of dawn redwood plots 2,3,and 5.According to the plot-level forest parameters listed in Table 1,poplar plots 1 and 4 have relatively high stand densities and average tree heights,thus,their mean distance residuals are comparable(the difference is 2.1 cm).By contrast,the stand density of dawn redwood plot 3 was approximately half that of plot 2,whereas the difference between their mean distance residuals was 1.9 cm.Although the stand densities of poplar plots 1 and 4 were relatively comparable to those of dawn redwood plot 3,the differences in the mean distance residuals between them were 7.6 and 9.7 cm,respectively.Moreover,the stand density of dawn redwood plot 2 and poplar plot 7 was 489 and 444 ha-1,respectively,and the mean tree height of plot 7 was greater than that of plot 2.The difference in mean residuals between the two plots was 10.9 cm.Thus,the method performed well on different stand properties with comparable coregistration accuracy.

Fig.15 shows an example of point cloud co-registration for two cases:deciduous(top row)and dawn redwood plots(bottom row).It can be observed that the horizontal and vertical discrepancies between the point cloud pairs are very low.Moreover,the trunks are fairly visible in the ground-based dataset(red),whereas the treetops are considerably distinct and dense in the ULS dataset(green).It is expected that the fusion results will benefit from the complementarity of datasets acquired from platforms with different perspectives.

In order to investigate the effect of the differences of the point density between ground-based data and ULS point cloud,the matching rate was compared in the case of original and downsampled ground-based data.It was found that the matching rate was improved by a range of 8%–15%at all plots after downsampling the ground-based LiDAR data.Thus,proper downsampling is required as a pre-processing step for the higher density point cloud.In addition,the co-registration results were compared to those of two previous studies(Guan et al.,2019;Polewski et al.,2019)which relied on tree locations as the keypoints.Guan et al.(2019)retrieved the correspondence from the matching of TIN formed by tree locations to co-register BLS,UAV-LiDAR,and multi-scan TLS for two sites of dawn redwood tree species.The reported distance residuals after coarse registration were 84 and 93 cm for sites I and II,respectively.Our study achieved a maximum of 75 cm for all distance residuals in the dawn redwood plots,as shown in Fig.14.Polewski et al.(2019)co-registered BLS and UAV-LiDAR data of seven sample plots(i.e.four deciduous plots and three dawn redwood plots)from a subtropical forest based on the distances between the tree locations and obtained the rigid 3D transformation by simulated annealing optimization.The recorded matching percentages of deciduous plots ranged from 36%to 48%,and the average residuals between the matched points varied from 62 to 67 cm.In our study,the range of matching percentages achieved at the deciduous plots was 37%–73% and the range of mean distance residuals was 41.3–46.5 cm.It is shown that the co-registration of deciduous plots is improved in terms of both matching rate and accuracy,implying that virtual keypoints could outperform tree locations.Both quantities are also compared for the dawn redwood plots and the matching rate of dawn redwood plots of the results obtained in our study ranged from 39% to 56% and the distance residuals ranged from 51.1 to 54.1 cm which did not improve the co-registration compared to the baseline method that yielded matching rates ranging from 46%to 72%and average distance residuals ranging from 27 to 36 cm.This can be attributed to the existence of distinct treetop shapes in dawn redwood species.

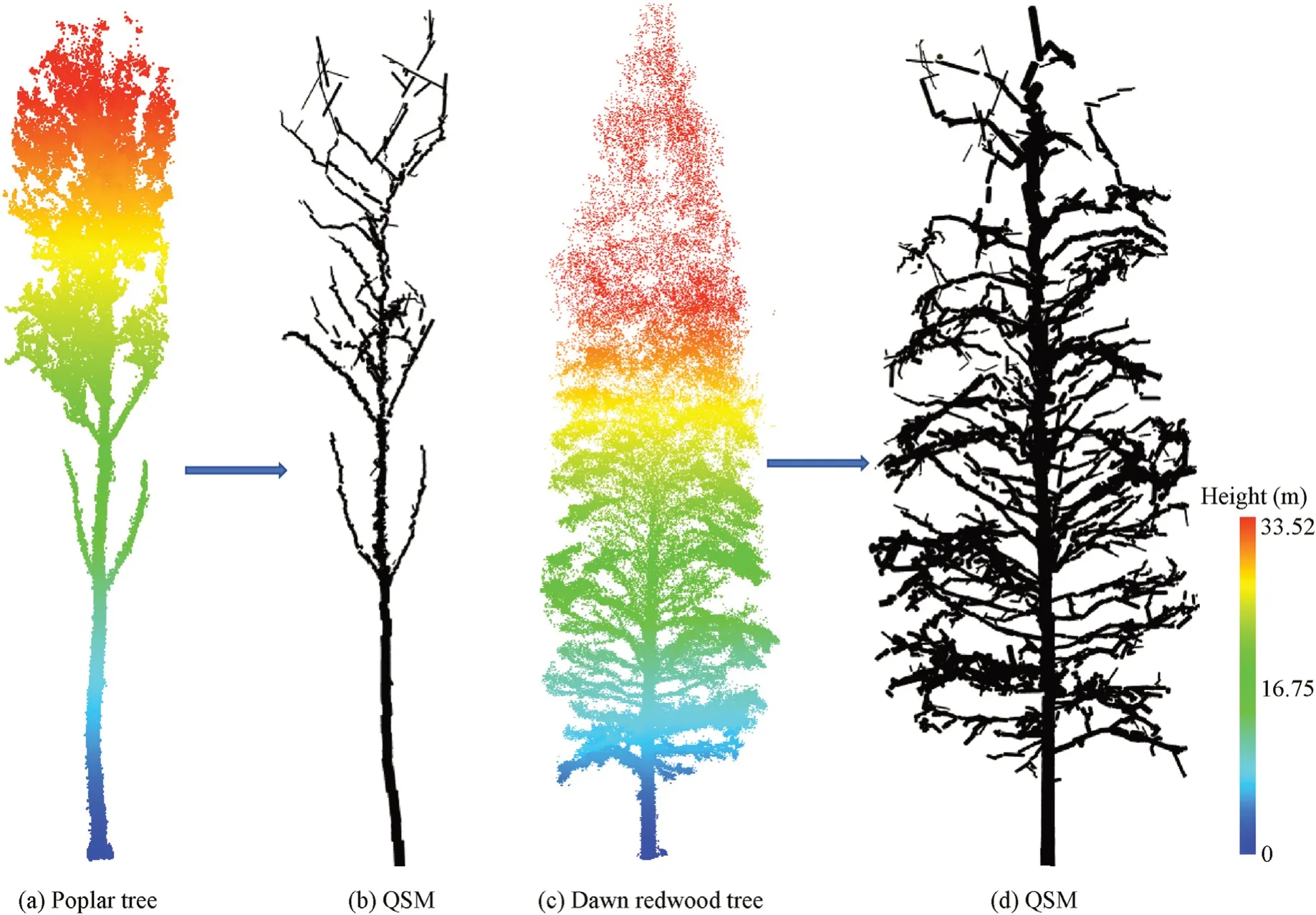
Fig.13.Tree modeling based on the TreeQSM algorithm.(a)and(b)poplar tree.(c)and(d)dawn redwood tree.

Fig.14.Distribution of distance residuals at the matched keypoints of each plot.Red lines:median of residuals.Filled circles:mean of residuals.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

6.2.Tree parameter estimation

Fig.15.Profiles along poplar(top row)and dawn redwood(bottom row)plots,with the right column showing the results of point cloud co-registration.Source point cloud:ground-based dataset(red color).Target point cloud:ULS dataset(green color).(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

The tree parameters were estimated by modeling the corresponding trees from the ground-based LiDAR and fused point clouds based onTreeQSM.The main advantages of using theTreeQSMalgorithm in tree modeling are that it made no assumptions about the different tree species or architectures,and the fast retrieval of all tree parameters including the tree volume based on trunk and branches,trunk length and its taper function,the bifurcation frequency,topology,and branching angles.Other tree parameter estimation methods focused on single parameters such as DBH,tree height or crown attributes while no information about the branches or bifurcation frequency.The computed evaluation metrics are summarized in Table 3.Fig.16 and Fig.17 show the correlation between the estimated tree parameters from ground-based and fused LiDAR point clouds with respect to field data for poplar and dawn redwood trees,respectively.Generally,it was found that fusion-derivedH,V,and CV were strongly correlated with field data based onR2compared to ground-based LiDAR only.Additionally,therRMSE for the aforementioned parameters were enhanced(H=9.01%,V=5.28%,CV=18.61%).Such improvements can interpret the more precise parameter estimation from fusion compared with the ground-based dataset.By contrast,fusion-derived DBH and CA were not significantly improved in terms ofrRMSE(DBH:-0.5%,CA:2.01%)compared with ground-based data.It is worth mentioning that fusion-derived DBH was not improved compared to ground-based DBH because the stems could not be sampled from the ULS data.The fusion-derived CA did not report a strong improvement because the crown base was independent of the clumped canopy.

Table 3Evaluation metrics of estimated parameters based on field measurements.

Based on the plot parameters,it is worth noting that the stand density of dawn redwood plots was relatively higher than that of the poplar plots.Therefore,the clumped canopy of dawn redwood plots would weaken ground-based LiDAR penetration to higher tree levels and vice versa for ULS.In view of this,the tree parameter estimation of poplar plots gained less benefit than that of dawn redwood plots.For instance,therRMSE ofHand CV was improved by up to 4.87% and 1.63%,respectively,compared to 9.01%and 18.61%for dawn redwood species.By contrast,therRMSE improvement inVfrom poplar trees was slightly better than that of dawn redwood trees(by 0.41%),which could be attributed to the thicker poplar trees than dawn redwood.Higher tree levels were mainly sensed by the ULS.Accordingly,thinner trunks/branches would not be well sampled,and thus could not be modeled by cylinder fitting throughTreeQSM.TherRMSE of fusion-derived CA was not significantly improved for either tree species(dawn redwood:0.75%,poplar:2.01%)because the crown base is accessible from the bottom levels by groundbased LiDAR independent of canopy clump.In addition,the CV of poplar trees benefited less from fusion(1.61%)than dawn redwood(18.61%)based onrRMSE because of the clumped canopy.It can be concluded that ground-based/ULS LiDAR data fusion has strong potential for tree parameter estimation,particularly in dense canopies.It is worth noting that all of these benefits were based on single-flight ULS data.Thus,multiple-fight ULS data would be more beneficial to tree parameter estimation from ground-based/ULS LiDAR data fusion because higher tree levels(thinner trucks and branches)would be better reconstructed from higher-density point clouds.

Fig.16.Scatterplots of estimated tree parameters and field measurements of poplar species.Top row:ground-based LiDAR data.Bottom row:fused point cloud.

Fig.17.Scatterplots of estimated tree parameters and field measurements of dawn redwood species.Top row:ground-based LiDAR data.Bottom row:fused point cloud.

Moreover,the performance of fusion-derived tree heights and ULSderived tree heights were compared to the field measurements.For poplar trees,therRMSE of ULS-derivedHcompared to reference field measurements was 3.96% while its counterpart from fusion was 3.76%which means that ULS-derived tree height did not significantly benefit from fusion.Similarly,the ULS-derivedHof dawn redwood trees was not remarkably changed compared to fusion-derivedHbecause theirrRMSEs were 4.73%and 4.58%,respectively.This could be attributed to the ULS data collection perspective where the treetops and higher-canopy levels are effectively scanned from above however,theR2andrRMSE of fusionderivedHslightly outperformed those from ULS only by a maximum 0.04 and 0.2%,respectively as shown in Fig.18.

According to Table 2,there was a large difference in point density between the ground-based dataset and ULS data.The tree structural modeling was greatly affected by the point density because the TreeQSM algorithm constructs the different tree segments based on the PatchDiameter 1 and 2.PatchDiameter2 determines the smallest tree element which can be modeled.Considering that trunks and branches account for the majority of tree volume,its improvement depends on how much trunk and branch volumes can be derived from ULS.Despite the groundbased/ULS data fusion,the tree volume has been improved by 5.28%.This could be attributed to the relatively low point density of ULS data which was not adequate to model the thin branches at high-tree levels.The crown volume has been calculated for the outer perimeter of the crown therefore,the ULS point density has been sufficient to model the surface shape of the crown.Consequently,the crown volume has significantly improved(18.61%)due to the ground-based/ULS data fusion.

Moreover,the LiDAR DEM accuracy is influenced by different factors including the sampling density of LiDAR,the morphological complexity of the terrain,the interpolation algorithm,and the land cover(Cǎeanu and Ciubotaru,2021).The existence of dense shrubs downgrades the DEM accuracy because it prevents the well sampling of the ground-level due to the sensor penetration capability and the LiDAR samping density.It was proved that the DEM generation in case of near-flat terrain was not significantly affected by the existence of shrubs.In addition,in case of rough terrain topography,the shrubs effect on DEM generation can be reduced by lowering the flight altitude and narrowing the scan angle(Chen et al.,2022).Thus,the proposed registration method can be utilized in such situation using repeated-flight ULS at different scan angles at relatively low flight altitudes.In this study,the experiments included forest plots from a planted forest that had a near-flat terrain,so the effect of terrain and topography was not significant.Moreover,the ULS flight altitude was relatively low(86 m)thus enabled a sufficient representation of the ground level.

Fig.18.Scatterplots of the ULS-derived heights versus field measurements.(a)Tree heights of poplar species.(b)Tree heights of dawn redwood species.

From a dataset point of view,structural tree parameter estimation based on point clouds was performed using either photogrammetric point clouds from a UAV(Ye et al.,2019;Shimizu et al.,2022)or LiDAR point clouds(Brede et al.,2019;Terryn et al.,2022).For instance,Terryn et al.(2022)compared the DBH,H,CA,and CV of a tropical forest from TLS and ULS to TLS/ULS data fusion as a benchmark,with the exception of DBH(RMSE=5.04 cm),which was compared to census data.This study also investigated the effect of single-and multiple-return ULS on parameter estimation.DBH and tree height were estimated based on least-squares circle fitting and height difference between the highest and lowest points of the tree point cloud,respectively.Their results were obtained for only the largest trees in all plots,and they did not report any improvements inH,CA,or CV owing to fusion.For instance,both TLSand ULS-derivedHreported a difference of≤1% compared with the benchmark.Similarly,CA and CV did not record improvements for both TLS(RMSE:3.06 m2,29.63 m3)and ULS(RMSE:<5.5 m2,30.33 m3).This can be attributed to the fact that they considered fusion-derived parameters as benchmark.By contrast,our fusion-derivedHand CV showed remarkable improvements in terms ofrRMSE of up to 9.01%and 18.61%,respectively,compared to real field data.Additionally,DBH was only estimated from the TLS data because stems were not sampled from the ULS dataset.

In addition,Shimizu et al.(2022)estimated the tree parameters from TLS and TLS/UAV-photogrammetric data fusion in a Japanese managed forest of coniferous species.DBH was estimated based on circle fitting,whereasHwas estimated based on matching CHM-derived treetops with TLS tree locations.They reported that fusion-derivedHwas remarkably improved by 6.2%,whereas DBH was not estimated from fusion(TLS:rRMSE=5.6%).Our findings are in line with these results because fusion-derivedHwas improved by 9.01%,and therRMSE of DBH from ground-based LiDAR was 5.77% for dawn redwood(coniferous)trees.Our fusion-derivedHoutperformed because matching CHM-detected treetops and TLS tree locations might involve false matches,which affects the fusion and parameter estimation results.In addition,Ye et al.(2019)investigated the potential of UAV photogrammetric point clouds for the QSM of single trees to assess woody biomass in both leaf-on and leaf-off seasons.They collected data using an oblique camera to increase point density.Despite their promising results,which showed that the UAV point cloud could precisely estimate tree parameters,the biomass was underestimated by approximately 49%.Even with low-cost and large-scale data collection,the change in sunlight intensity and poor radiometric quality because of cloudy weather still pose major challenges.By contrast,owing to its penetration capability,the UAV-LiDAR can sense under-canopy levels;however,with a lower point density compared to higher canopy levels.Therefore,fusion with ground-based LiDAR systems is expected to not only improve data completeness but also increase the point density at the lower canopy level,which was achieved in our study.The fusion-derivedVimproved by up to 5.28%.Such improvement can be justified by the ground-based/ULS LiDAR data fusion,as the ULS enhanced the sampling of the high canopy level.

Moreover,Brede et al.(2019)compared the capability of ULS data in tree parameter estimation usingTreeQSMto TLS.It was found that the trunks and branches of diameter≥30 cm were modeled well using UAV-LiDAR with a RMSE of 1.12 m3,whereas smaller branches led to volume overestimation by an average of 41.3%.The study showed the strong impact of clumped canopy on ULS-derivedVbecause the tree trunk was characterized by sparse points with an increased RMSE by 6.6 m3.Based on these findings,it is worth noting that structural modelling of single trees from ULS data of dense canopies was extremely challenging.Therefore,we used the fusion of UAV and ground-based LiDAR systems in our study for the precise representation of trees.Our results showed that the fusion-derivedVimproved(5.28%)in terms ofrRMSE.Thus,ground-based/ULS LiDAR data fusion is required to complete and enhance point cloud representation,particularly in dense forest stands.

Tree height is a key contributor to the AGB estimation of single trees.A comparative study(Laurin et al.,2019)investigated the performance of ALS,TLS,and UAV photogrammetry point clouds for tree height estimation.They reported that tree height underestimation was expected from the three datasets owing to instrumental limitations and/or local forest conditions.They proposed that the integration of different systems would lead to a more rigorous estimation of the tree height.A similar finding was also corroborated in Liang et al.(2019)and Brede et al.(2017).In our study,the dawn redwood plots had a clumped canopy,and the fusion-derivedHwas improved by 9.01% in terms ofrRMSE.Consequently,ground-based/ULS LiDAR data fusion is an effective solution for volume and/or tree height estimation in complex forest environments.

It is also worth noting that the experimental results were obtained in plantation forests with homogeneous forest structures,such as monotype tree species and principally equivalent tree attributes.By contrast,a natural forest preserves complex sample plots with mixed species and a wide variety of tree patterns and attributes.Such discrepancies would pose a critical challenge to the QSM of trees dependent on a single LiDAR platform.For instance,understory trees cannot be sampled from the ULS point cloud,whereas treetops of large trees cannot be captured using ground-based LiDAR.Hence,tree parameter derivation based on groundbased/ULS LiDAR data fusion is of great importance,particularly for natural forests,where the fusion will reveal the entire 3D extent of the tree by compensating for the deficiency of individual platforms.

In addition,multi-layer forest is one type of high complexity to existing LiDAR data registration approaches particularly in case of ground-based/airborne LiDAR data integration.On the one hand,there will be many understory trees that are not expected to be extracted from airborne LiDAR date due to the sensor penetration capability and dense understory.Thus,the tree location matching between ground-based and airborne LiDAR data will be challenging because there are a lot of tree locations that have no counterparts in those from airborne LiDAR data.On the other hand,the extraction of virtual keypoints would be challenging in such forest type however the removal of under-canopy will decrease the number of understory trees before the keypoints extraction.Accordingly,only relatively high trees will be used for keypoints extraction based on canopy analysis to co-register the point cloud pair.However,the proposed method requires further investigations against such forest types.

7.Conclusions

In this study,a holistic framework for 3D tree modelling using ground-based/ULS LiDAR data fusion based on QSM was developed.In general,the use of virtual keypoints for co-registration significantly alleviated the limitations in tree localization,particularly in the case of ground-based/ULS LiDAR co-registration,where the stems were only identified appropriately from the ground-based LiDAR dataset.The experimental results of a subtropical plantation forest,including poplar and dawn redwood trees,showed that the fusion-derivedH,V,and CV were remarkably improved,whereas DBH and CA were the least profited.Moreover,fusion-derived tree parameters of dawn redwood plots were significantly improved compared to those of poplar trees because of the relatively higher stem density of dawn redwood plots.Such improvements in the fusion-derived tree parameters,particularly tree height,would improve AGB estimation because tree height is a key contributor to AGB estimation.Such a fusion scheme can be further investigated in a more complex natural forest where there is a high variety of tree parameters at the plot level,which may include mixed tree species.This diversity provides an opportunity to further examine the performance of point-cloud fusion and biophysical parameter estimation.

Acknowledgment

This work was supported by the National Natural Science Foundation of China(Project No.42171361),the Research Grants Council of the Hong Kong Special Administrative Region,China,under Project PolyU 25211819,and in part by the Hong Kong Polytechnic University under Projects 1-ZE8E and 1-ZVN6.