基于DFT和DTFT插值的正弦信号频率估计
吴 会 豪, 樊 磊, 宋 焕 焕, 兰 振 平, 李 萍
( 大连工业大学 信息科学与工程学院, 辽宁 大连 116034 )
0 引 言
加性白噪声背景中的正弦信号频率估计,是数字信号处理领域的一个基本且重要的研究课题,在通信、雷达、声呐、电子测量、仪器仪表、电力系统、线性系统识别等领域都有着极为广泛的研究与应用[1-16]。在这些领域的典型应用系统中,接收信号的模型多为正弦信号,对正弦信号频率进行估计的算法性能是这些研究与应用的关键和重要的基础,甚至决定了整个系统的可用性。
现有的正弦信号频率估计算法可以分为两大类:时域估计算法[1-4]和频域估计算法[5-16]。时域估计算法中,Rife等[1]提出的最大似然估计算法,估计误差可以达到理论下限值,即克拉美罗下限,但算法十分复杂,运算量大。Kay[2]提出了使用采样序列的相位差估计频率的方法,虽然解决了相位模糊问题,但是信噪比阈值比较高。Tu等[3]提出了一种基于相位校正自相关的频率估计方法,通过计算所构造的误差函数的最小值得到频率估计值。整体上看,时域估计算法的共同问题在于运算复杂度高,对硬件要求高,无法在一些需要进行实时处理的场景中得到很好的应用。
频域估计算法通常利用离散傅立叶变换进行正弦信号频率估计,是一种极为有效的方法。离散傅立叶变换处理可以带来信噪比增益,在信噪比较低的情况下,估计的精度依然较好。而且基于离散傅立叶变换的频率估计算法可以利用快速傅立叶变换(fast Fourier transform,FFT)来实现更高效的运算,更加适用于需要实时处理的场景之中。基于离散傅立叶变换的频率估计方法一般分两步进行。首先,对接收到的正弦信号采样序列进行离散傅立叶变换,搜索离散傅立叶变换的幅度最大谱线实现粗估计。然后,采用离散傅立叶变换幅度最大谱线附近的若干谱线对信号频率进行插值,即进行进一步的精估计。现有的基于离散傅立叶变换的频域估计算法,一般只是在精估计阶段采用的插值策略有所不同。Quinn[5]通过对三个连续的离散傅立叶变换系数进行复插值,获得了频率的估计值,但是在相对频率偏差接近0时估计误差较大。Candan[6]利用离散傅立叶变换幅度最大谱线及其左右两侧相邻的两根谱线来实现精估计,算法在采样点数较少时也可保持较稳定的性能,但是精度并不是很高。Yang等[7]提出了一种三谱线合理组合的非迭代频率估计方法,先对采样序列进行N点时域补零,再进行2N点FFT,然后按照最小二乘法思想,采用幅度最大的三根谱线进行频率插值,由于在估计表达式推导过程中使用了泰勒级数展开,并忽略了高阶项,导致了估计偏差的产生。Fang等[8]提出对信号采样序列补零填充后进行2N点FFT,并采用第二大和第三大谱线来对信号频率进行精估计,该算法估计精度高于Candan算法,但对信号进行时域补零填充,带来了运算量的增加。Aboutanios等[9]采用位于幅度最大谱线和次大谱线中点位置,以及幅度最大谱线和第三大谱线中点位置的两点DTFT采样值进行精估计,并且通过迭代,使得估计精度得到很大的提高,但是,随着迭代次数的增加,计算量会逐渐增大。Serbes对文献[9]中的AM算法进行了改进,先采用文献[10]中无偏的AM算法进行第一次迭代,然后采用对称地位于最大谱线两侧的两点DTFT采样值进行频率插值,即HAQSE算法[11],使得估计精度进一步提高。
现有的基于离散傅立叶变换的频域插值估计算法,所使用的谱线不论具体位置如何,也不论谱线数量的多少,采用的都是对称地位于离散傅立叶变换最大谱线两侧的若干谱线。这样一来,所采用的谱线中,必然会有幅度小于最大谱线的,这样的谱线在低信噪比时,比较容易受到噪声的影响,从而导致算法估计性能的下降。因此,本研究提出了一种基于离散傅立叶变换和DTFT插值的正弦信号频率估计算法,采用离散傅立叶变换最大谱线及其同侧的两根DTFT谱线来对频率进行插值。并采用迭代算法,以提高算法的估计精度。迭代后,所采用的谱线幅度均不小于离散傅立叶变换最大谱线幅度。
1 三谱线插值的正弦信号频率估计算法
加性白噪声背景中,单一频率的复正弦信号[10]可以表示为
x(n)=s(n)+w(n),n=0,1,…,N-1
(1)
s(n)=Aej(2πf0n/fs+θ0),n=0,1,…,N-1
(2)
式中:s(n)为待估计的正弦信号;w(n)为均值为0、方差为σ2的加性白噪声;N为信号长度,即采样点数;A、f0和θ0分别为信号的幅度、频率和初始相位;fs为采样频率。
对待估计的正弦信号s(n)进行N点离散傅立叶变换[14]可以得到:
(3)
式中:k=0,1,…,N-1;m是离散傅立叶变换频谱中幅度最大谱线的离散频率索引值。
经过离散傅立叶变换的正弦信号频率可以表示为
f0=(m+δ)Δf
(4)
式中:δ为离散傅立叶变换幅度最大谱线与信号频率之间相对频率偏差,δ∈(-0.5,0.5)。Δf=fs/N,为离散傅立叶变换的频率分辨率,即离散傅立叶变换频谱中相邻谱线的频率间隔。
基于离散傅立叶变换插值的正弦信号频率估计方法是通过搜索信号离散傅立叶变换频谱中幅度最大谱线S[m]的位置,得到信号频率的粗估计值为m·Δf。对f0进行精估计,即对相对频率偏差(δ)的估计。
为了表达简便,统一将S[m+k]记为Sk。这样离散傅立叶变换频谱中的幅度最大谱线的表达式为
(5)
现有的频域估计算法,采用的都是离散傅立叶变换幅度最大谱线S0和对称地位于S0两侧的若干谱线来对相对频率偏差(δ)进行估计。谱线在低信噪比时,比较容易受到噪声的影响,从而会导致算法估计性能的下降。为了获得性能更好的频率估计算法,利用离散傅立叶变换幅度最大谱线S0的幅度|S0|以及信号频谱在离散频率轴m+0.1和m+0.2(或者m-0.1和m-0.2)处的两根DTFT谱线幅度|S0.1|和|S0.2|(或者|S-0.1|和|S-0.2|)来对相对频率偏差δ进行估计。由于信号s(n)的N点离散傅立叶变换离散频谱只出现在离散频率k取整数值的位置,所以S0.1和S0.2不能直接利用离散傅立叶变换计算。为了得到这两根谱线,可以利用s(n)的DTFT来计算。
序列s(n)的DTFT[15]表示为
(6)
式中:ω为数字角频率。
考虑到信号观测为一个周期,即0~T,采样后序列s(n)范围0~(N-1),利用ω=2πfT/N将角频率替换为频率f,于是序列s(n)的DTFT可表示为
(7)
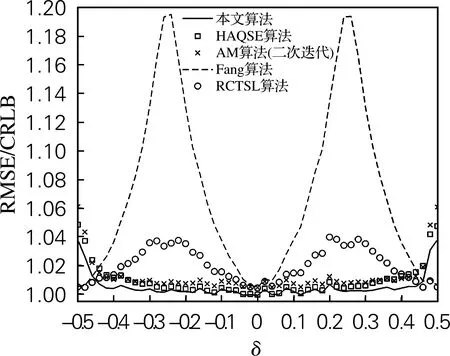
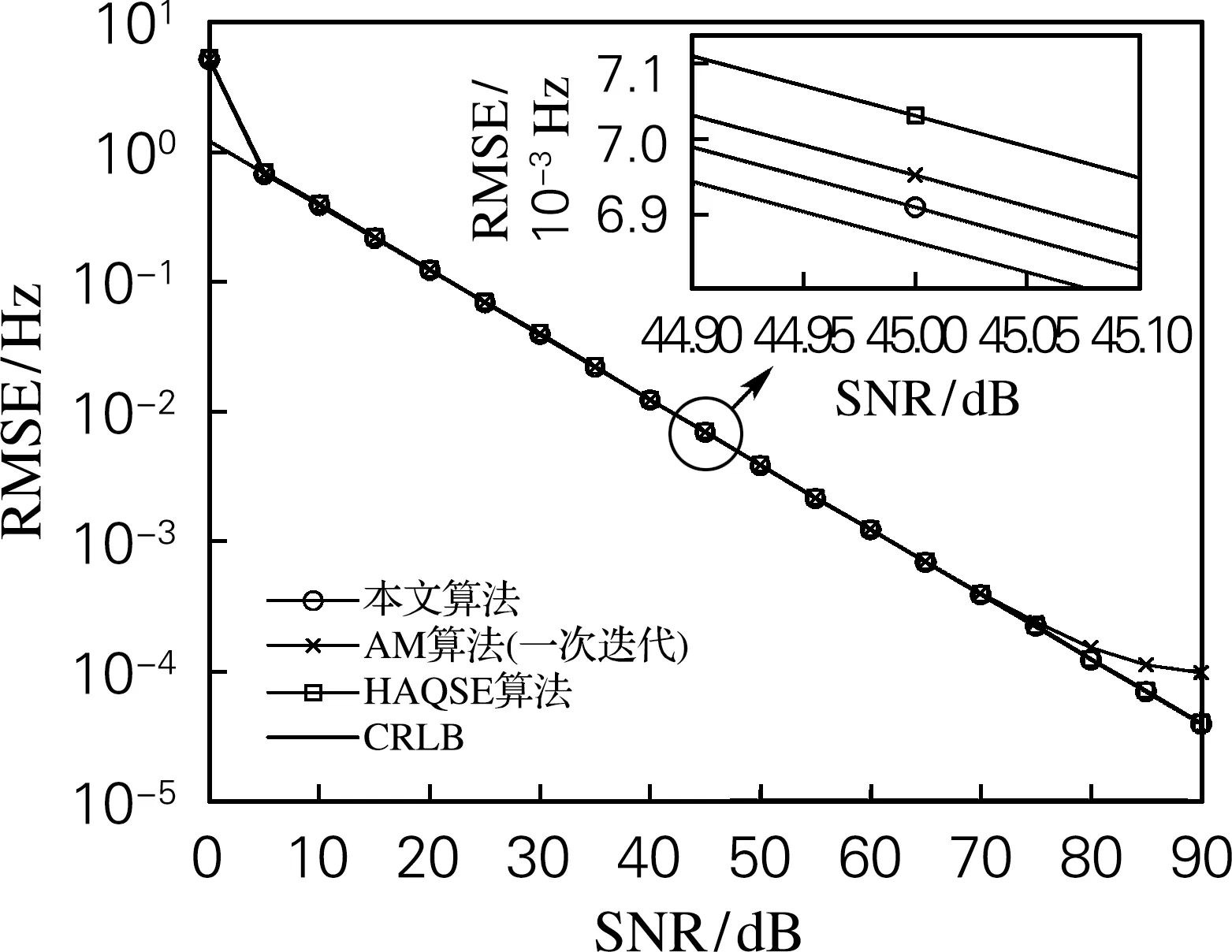
式中:0≤f 利用式(7)可以计算序列s(n)在任意频率f(f (8) 分别把f=(m+0.1)Δf和f=(m+0.2)Δf代入上式,可以求得两根DTFT谱线S0.1和S0.2的表达式如式(9)、(10)所示。 S0.1=S(f)|f=(m+0.1)Δf= (9) S0.2=S(f)|f=(m+0.2)Δf= (10) 于是,三条谱线的幅度|S0|,|S0.1|和|S0.2|的表达式如式(11)~(13)。 (11) (12) (13) 由式(11)~(13)可以得到 (14) (15) 整理可得: |S0|sin 0.1πcot πδsin 0.2π- |S0|cos 0.1πsin 0.2π (16) |S0|sin 0.2πcot πδsin 0.1π- |S0|cos 0.2πsin 0.1π (17) 式(16)减式(17)并整理可得: (18) 得到δ的估计表达式为 (19) 当使用最大谱线左侧的两条DTFT谱线S-0.1和S-0.2时,可得: (20) 将两种情况的表达式写作一个估计表达式如式(21)所示。 (21) 步骤1对x(n)进行N点FFT得到X[k],找到最大谱线X0; (22) U=-d,-d-0.1,-d-0.2 (23) 经该迭代算法迭代,d和最大谱线位置更新后,所采用的另外两根谱线的幅度均不小于最大谱线的幅度。因此所采用的三根谱线幅度均比较大,都不易受到噪声的影响,算法的频率估计性能得到了提升。 为了验证本研究所提出算法的性能,通过仿真实验,将提出算法的性能与现有同类算法以及CRLB进行比较。用于进行对比的各种算法包括Candan算法[6]、RCTSL算法[7]、Fang算法[8]、AM算法[9]和HAQSE算法[11]。其中Candan算法是现有不补零且不迭代算法中性能最好的,RCTSL算法和Fang算法是两种典型的时域补零算法,AM算法和HAQSE算法是现有的基于离散傅立叶变换插值算法中精度很高的算法。各种算法对相对频率偏差δ的估计表达式见表1。 表1 各种算法的估计表达式 当复正弦信号的幅值、频率和初始相位未知时,克拉美罗下限可以表示为[1] (24) 当f0=(N/4+δ)fS/N,N=8时,在无噪声的条件下,本算法与现有几种算法的频率估计偏差与相对频率偏差δ∈(-0.5,0.5)之间的关系如图1所示。从图中可以看出,本算法与HAQSE算法的估计偏差在δ∈(-0.5,0.5)始终为0,表现优于其他算法。AM算法、Fang算法以及RCTSL算法在δ=0时相对频率偏差接近0,但都在δ的整个取值范围内不稳定。AM算法大约在|δ|=0.3时估计偏差达到最大。Fang算法大约在|δ|=0.25附近估计偏差达到最大值。RCTSL算法大约在|δ|=0.12和0.38时,估计偏差达到最大。 图1 各种算法估计偏差随δ的变化 当f0=(N/4+δ)fS/N,SNR=10 dB,N=32时,本算法与现有几种算法频率估计的均方根误差RMSE随相对频率偏差δ变化的关系如图2所示。从图中可以看出,当δ在(-0.5,0.5)整个区间范围内变化时,本算法频率估计的RMSE与理论下限值CRLB的比值始终接近于1,并且相较于现有算法而言更小。虽然在|δ|>0.45时,本算法的RMSE高于Fang算法和RCTSL算法,但本算法整体的RMSE表现要远远优于这两种算法。因此,本算法频率估计的精度高于现有算法。 图2 各种算法RMSE随δ的变化情况 当f0=(N/4+δ)fS/N,N=16,δ=0.2时,本算法与现有算法的均方根误差随信噪比(signal-noise ratio,SNR)的变化情况如图3所示。可以看出,当信噪比在0~90 dB时,本算法的RMSE始终接近CRLB,并小于其他算法的RMSE。一次迭代的AM算法在信噪比高于40 dB 的时候,开始逐渐偏离CRLB。RCTSL算法在信噪比高于50 dB时逐渐偏离CRLB。同样的,Fang算法和Candan算法在信噪比高于55 dB 时也开始偏离CRLB。在中低信噪比时Candan算法的估计精度要明显低于其他算法。因此,本算法的估计精度高于其他算法,并且在0~90 dB范围内保持稳定。 图3 各种算法的RMSE随信噪比的变化情况(δ=0.2) 当f0=(N/4+δ)fS/N,N=16,δ=0.2时,本算法、二次迭代的AM算法和HAQSE算法的均方根误差随信噪比的变化情况如图4所示。可以看出,当信噪比在0~90 dB范围变化时,本算法的RMSE小于其他两种算法的RMSE,并且始终接近CRLB。同时,当信噪比高于75 dB时,二次迭代的AM算法的RMSE逐步偏离CRLB。AM与HAQSE算法是现有算法中估计精度很高的算法。本算法的估计精度高于这两种算法。 图4 本算法、AM算法和HAQSE算法的RMSE随信噪比的变化情况(δ=0.2) 当f0=(N/4+δ)fS/N,N=16,δ=0.4时,本算法与其他算法的RMSE随信噪比的变化情况如图5所示。从图中可以观察到,当SNR从0变化到90 dB时,本算法的误差小于其他算法,并且始终接近CRLB。一次迭代的AM算法和Candan算法的RMSE曲线在SNR高于45 dB时,开始逐渐远离CRLB曲线。还可以观察出,Fang算法和RCTSL算法的RMSE曲线分别在信噪比高于75和85 dB时开始远离CRLB曲线。除此之外,在中低信噪比时,Candan算法的RMSE曲线要高于所有其他算法。 图5 各种算法的RMSE随信噪比的变化情况(δ=0.4) 当f0=(N/4+δ)fS/N,N=16,δ=0.4时,本算法、二次迭代的AM算法和HAQSE算法的RMSE随信噪比的变化情况如图6所示。可见,当SNR从0变化到90 dB时,本算法的RMSE低于其他两种算法的RMSE,并始终接近CRLB。还可以观察到,当信噪比高于80 dB时,二次迭代的AM算法的RMSE曲线会逐渐远离CRLB。本算法的估计精度高于另两种算法。 图6 本算法、AM算法和HAQSE算法的RMSE随信噪比的变化情况(δ=0.4) 各种算法的运算量如表2所示,其中AM算法按照2次迭代统计。从表中可以看出,本算法的运算量要小于RCTSL算法、Fang算法、AM算法以及HAQSE算法。其中RCTSL算法和Fang算法均是基于时域补零和2N点离散傅立叶变换的算法,运算量要高于不进行时域补零的其他算法。Candan算法的运算复杂度低于其他算法。但是从图3~6仿真结果可知,Candan算法的估计精度是所有方法中最低的,并且在高信噪比时表现不佳。 表2 各种算法的运算量 本研究提出的基于离散傅立叶变换和DTFT三谱线插值的复正弦信号频率估计方法在精估计阶段,使用离散傅立叶变换最大谱线及其同侧的两根DTFT谱线来对频率进行插值。并采用了迭代算法,以提高算法的估计精度。仿真结果表明,当信噪比从0变化到90 dB时,算法的估计误差小于现有同类的离散傅立叶变换插值算法,并始终保持接近CRLB。在高信噪比的条件下,算法的估计精度优势更为明显。此外运算量分析表明,算法的运算量低于RCTSL算法、Fang算法、AM算法和HAQSE算法。因此,本算法比现有的方法更加适用于实时处理的应用场景之中。

2 迭代算法

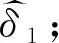
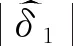


3 仿 真






4 结 论

