考虑时变特性的海上溢油事故应急物资调度

张昊，陶宁蓉*,2，杨男

(1.上海海洋大学，工程学院，上海 201306；2.上海海洋可再生能源工程技术研究中心，上海 201306)

0 引言

随着经济全球化的快速发展，各国经济越来越依赖于海上运输，然而海上事故频发，海上运输安全问题一直备受社会关注[1]。其中，最受关注的当属海上溢油事故。根据《1990 年国际油污防备、反应和合作公约》，海上溢油事故是指原油及其相关炼制品等油品进入海洋或河流的事故[2]。海上溢油事故作为一种突发事件，不仅会造成巨大经济损失，而且溢出的油品会严重污染海洋环境、破坏海洋生态。据统计，1973—2018 年，我国沿海港口共发生3336 起船舶溢油事故，平均每年发生76 起。因此，及时合理地调度溢油事故应急物资至关重要。

目前，国内外针对海上溢油事故应急物资调度的研究较少。张莉等[3]针对事故点的需求紧迫度，研究如何优先配送紧迫度高的事故点以降低总成本。郝国柱等[4]考虑海上溢油事故应急物资需求量和调度时间不确定，引入三角模糊函数，建立了总成本最小和调度时间最少的双目标优化模型。Zhang等[5]针对海上溢油事故多配送中心协同调度进行研究，提出一种基于粒子群优化的启发式方法。李松等[6]考虑各应急物资集散点和船舶并行作业的特点，将物资需求量转换为当量体积，以船舶航行时间最小为目标，建立了大型海上溢油事故应急物资联动调度模型。张聆晔等[7]统筹海上应急物资调度与陆上补给应急物资调度，构建两阶段应急物资动态优化调度模型，并提出混合启发式算法进行求解。汪强等[8]结合海上溢油事故特点，构建了应急救援中心供应充足条件下运输物资延误总时间最小的数学模型，并用遗传算法进行求解。

溢油事故发生时，受到气象条件和海况的影响，油品进入海洋后会漂移和扩散，进而导致救援需求点变动。应急救援如果不考虑需求点的漂移扩散特性，会造成救援船舶偏离需求点实际位置而影响救援方案实施。刘晓佳等[9]针对溢油的扩散性和应急物资需求的多样性引入三角模糊数确定应急物资需求区间，以船舶运输总时间最短为目标建立调度模型，并运用于遗传算法对其进行求解。李晶等[10]分析了海上油膜漂移特性和海上溢油点对救援物资需求量不确定的特点，建立救援成本最小、时间最短的双目标规划模型并求解。然而，以上研究都没有考虑油膜漂移扩散对应急调度路径规划的影响。王军等[11]考虑单一遇险目标受海上风浪影响产生漂移，建立了水陆两阶段应急物资优化调度模型，但是该研究在海上只有一个需求点，而海上溢油事故发生后的求援需求点通常是多个。Zhang等[5,12]考虑了多个需求点的救援，结合需求点的漂移特性提出了两阶段优化模型，分别采用了改进粒子群算法和基于改进粒子群算法的混合启发式算法进行求解获得Pareto解集，但是该研究在评估环境污染时没有涉及需求点漂移导致的油膜面积动态变化。

综上所述，已有研究大多没有在应急救援调度中考虑需求点受海上风浪影响而产生位置漂移的时变特性。本文在综合考虑海上溢油事故需求点漂移特性以及油膜扩散造成的环境损失后，建立最小化调度运输成本和环境污染损失的数学模型，并在传统遗传算法的变异操作中加入模拟退火的思想，提出改进的遗传模拟退火混合优化算法进行求解。

1 问题描述

当海上发生溢油事故时，相关部门首先迅速定位事故发生点，分析气象条件、海况、溢油类型、溢油规模等信息，计算溢油扩散数据和应急物资需求量；接着协调各应急救援中心做出调度安排；最后实施应急措施，对泄漏油品等污染物进行围控、回收、处理。如图1所示，本文研究的问题为：在海上溢油事故发生初期，如何调度多个应急救援中心的物资，对污染区域内多个动态需求点实施求援，从而将事故控制在较小范围，实现救援运输成本和环境损失的最小化。基本假设如下：

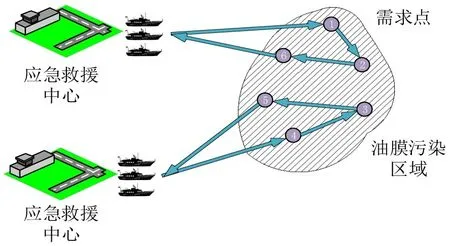
图1 海上溢油事故应急物资调度Fig.1 Emergency material scheduling for offshore oil spill accident

(1)溢油地位置、物资需求量和溢油地气象条件等基本信息可通过卫星技术计算获取。

(2)考虑油膜的漂移和扩散特性，事故存在多个求援需求点，且随着油膜的漂移扩散，需求点的位置是动态变化的。

(3)救援船舶为负责对溢油进行围控、导流的溢油工作船舶。

(4)当应急物资运送到需求点后救援工作即刻启动。

(5)海上没有设置中间节点进行船舶之间的物资交付。

(6)船舶在海上航行速度保持一致。

模型中符号说明如下。

(1)集合

V——海上溢油事故应急物资调度节点集合，V=A∪B，其中，A表示需求点集合，B表示应急救援中心集合；

K——应急救援船舶集合。

(2)参数

U——溢油总量；

T0——调度开始时间；

Qk——船舶k的最大运载能力；

qi——需求点i的需求量；

vk——船舶k的航行速度；

vi——需求点i的移动速度；

c1——单位距离运输成本；

c2——船舶调用成本；

ρw——海水密度；

ρ0——溢油密度；

β——风速与水平坐标的倾角。

(3)中间变量

S(T)——T时刻的溢油油膜面积；

θij——船舶从点i向j航行时，点i到点j之间的距离连线与j点漂移路径的夹角；

(4)决策变量

2 油膜漂移扩散分析

2.1 溢油油膜的扩散

关于海上溢油扩散行为的研究，目前最具代表性的是Fay 提出的三阶段扩展模型[13]。基于该模型，Leendertse[14]考虑风作为影响因素，通过溢油总量U、溢油事故等待救援时间t、海水密度ρw和溢油密度ρ0计算需求点油膜扩散速度，即

式中：Δρ=ρw-ρ0。

2.2 溢油油膜的漂移

依据溢油类型、溢油发生时间和地点、溢油量和持续时间等信息，计算油膜漂移的具体数值。本文基于Li等[15]的研究，认为油由大量质量相等的粒子构成，并受风、波浪和湍流扩散影响，则通过需求点i处的风速和洋流速度，计算需求点i的漂移速度为

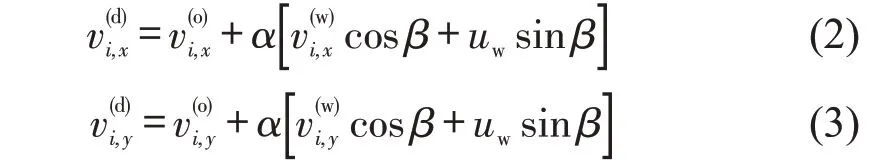
2.3 需求点时变位置分析

研究海上溢油事故救援需求点位置的时变特性，使应急调度方案与需求点实际位置匹配，是提高求援响应效率的前提与保障。图2 为需求点位置漂移示意图。

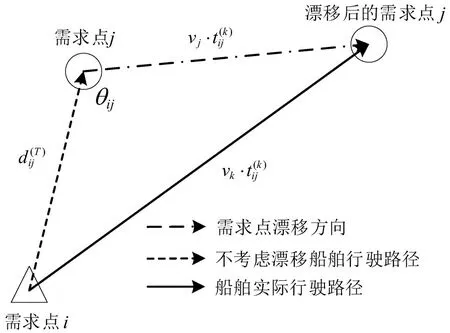
图2 需求点位置漂移示意图Fig.2 Schematic diagram of demand point location drift

根据油膜的漂移速度和方向、船舶行驶速度、应急救援中心/当前船舶所在的位置等信息可以计算船舶到达下一个目标点的时间以及该点的实际位置。如图2 所示，当救援船舶k从出发点i向目标点j行驶时，出发时刻两点间的距离为

三角形三边关系为

夹角θij的计算公式为

则已知需求点漂移速度和方向、船舶速度，可推出船舶所需航行时间为

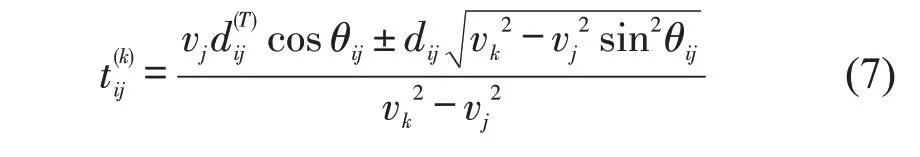
2.4 环境损失评估

大多数针对石油等有害物质造成的环境损失评估研究需要大量的数据和很长时间。为降低评估成本，本文采用弗罗里达公式[9]，该公式被证明是一种用于溢油生态损害评估的快速、低成本方法。环境污染损失E为

式中：E(T)——T时刻的环境污染损失；

R——基准利率；

店主懒洋洋按了播放，迪斯科和说唱又想起。警察一直耐心得听到了“送到派出所”，琢磨了半天，转身对左小龙道：“没问题啊，没反党啊。”

L——地理位置影响因素(沿海为8，近岸为5，离岸为1)；

M——特殊管理区域(是为2，否为1)；

A*——受影响动物栖息地的附加费用(按照生物类型，每平方米1～50元)；

PC——污染物特质(重油为8，中重油为4，轻油为1)。

由于本文研究关注油膜的漂移扩散特性，即油膜面积S随时间变化。当拦油类物资到达需求点实施救援后，油膜漂移扩散可得到有效控制，因此本文通过救援需求点的位置信息来计算某时刻t下的油膜面积S。如图3 所示，假设在时刻t跟踪到事故区域内的若干救援点，则油膜面积S的具体计算方法为：(a)获取时刻t的所有需求点位置信息；(b)根据离散点最小边界查找法确定边界点坐标；(c)用向量法计算油膜污染区域面积S。

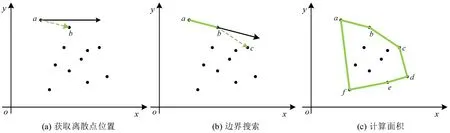
图3 最小边界查找示意图Fig.3 Schematic diagram of minimum boundary search

式中：a,b,…,f——确认后的边界点坐标信息。

2.5 数学模型

2.5.1 目标函数

基于以上分析，本文模型的优化目标为最小化应急救援运输成本和环境损失，即

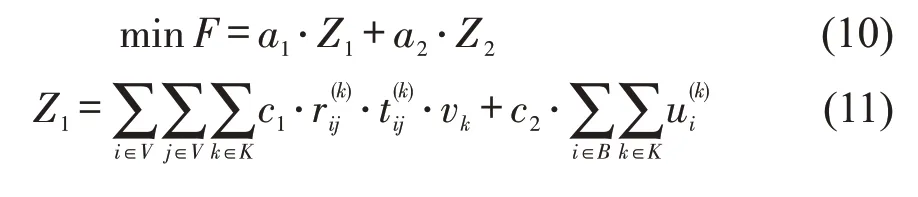
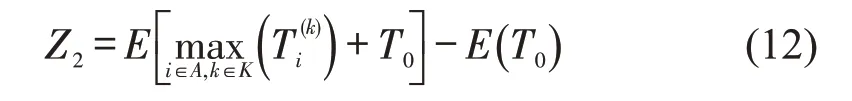
式中：a1、a2——权重系数，a1+a2=1；

Z1——应急救援运输成本，如式(11)所示，该部分包括派出救援的船舶固定成本和油耗成本；

Z2——环境污染损失，如式(12)所示，取救援实施前后的差值；

c1——单位距离运输成本；

c2——船舶派遣成本；

E(T0)——救援前的环境污染值；

E——所有需求点的救援工作到位后的环境污染值。

2.5.2 约束条件

式(13)表示船舶k的 载重约束。式(14)和式(15)为救援需求点距离约束，式(14)表示船舶k在需求点i时，需求点i,j之间的距离；式(15)表示船舶k由i到j的实际航行距离。式(16)和式(17)为时间约束，式(16)表示若船舶k不经过i点，则=0；式(17)表示船舶k由i到j的运输时间为船舶k到达j点的时刻减到达i点的时刻。式(18)和式(19)是对求援船舶出发点的约束，式(18)表示每艘救援船的出发点必须是应急救援中心；式(19)表示每艘救援船仅能从多个应急救援中心的其中一个出发。式(20)约束救援船不可在应急救援中心之间往返。式(21)表示救援船在各救援需求点的流量守恒。式(22)表示每个救援需求点只需一次救援。

3 算法设计

本文模型属于多中心多需求点且需求点漂移的路径规划问题，而路径规划问题已被证明是NP-hard问题，在实际应用中，这类问题很难在有限时间内通过精确算法求出高效解。遗传算法是一种强鲁棒性的启发式随机搜索算法，具有较好的全局搜索性能，但基本遗传算法存在过早收敛于局部最优解的现象，而模拟退火算法通过以一定概率接受“劣等解”具有较好的局部搜索能力。因此本文采用基于遗传算法和模拟退火算法的混合算法，在遗传变异操作中引入模拟退火思想，通过多策略变异方法对个体进行连续多次变异并以一定概率接受差解，算法流程如图4所示。

图4 遗传模拟退火算法流程图Fig.4 Flow chart of genetic and simulated annealing algorithm

3.1 编码与解码

本文编码采用整数编码方式，染色体为J+I-1(需求点数+应急物资中心点数-1)的整数序列，其中，数值1～J分别为需求点编号，而J+1～J+I-1 的数值为应急物资中心的分割码。以8 个需求点、2 个应急物资中心为例，数值9 为2 个应急物资中心的分割码，如图5所示。

图5 染色体解码示意图Fig.5 Schematic diagram of chromosome decoding

解码时，从染色体的第1 个需求点7 开始累加物资需求量，假设到需求点5累加的需求量超过船舶载重，则在需求点5 前断开，则7-3-2 由1 号应急物资中心的船舶1 求援，从需求点5 开始重复上述操作。最终解码的救援方案为1 号应急物资中心船舶1的路径为0-7-3-2-0；船舶2的路径为0-5-4-0；2号应急物资中心船舶1的路径为0-6-1-8-0。

3.2 适应度函数

各个染色体的适应度值由模型的目标函数构建，目标函数值越小，适应度越大。

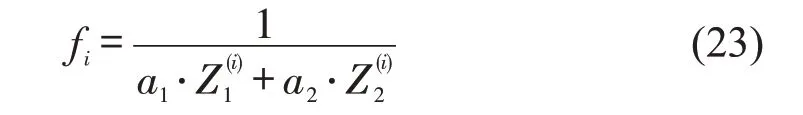
式中：fi——染色体i的适应度值；

假设当前需求点序列为0-7-3-2-0，如图6 所示，首先，获取救援中心0和需求点7的位置以及需求点7 的漂移方向和速度，根据式(7)计算0-7 的运输时间，记录船舶1 行驶距离·vk；更新时刻剩余需求点的位置；基于更新后的各点位置以及下一个需求点3的漂移速度和方向，计算下一步运输时间和距离，如图6(b)所示，重复以上操作直到船舶返回应急救援中心，计算Z1。在救援结束后获取所有需求点更新后的位置信息，根据最小边界查找法获得油膜面积，计算Z2。

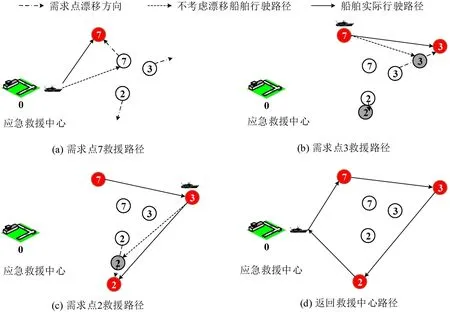
图6 船舶救援路径示意图Fig.6 Schematic diagram of ship rescue route

3.3 选择操作

选择操作采用精英保留策略和轮盘赌策略，将种群中的个体按照适应度大小排序，通过精英保留策略保留适应度最大的若干个体。剩下的个体采用轮盘赌策略，即将剩余个体适应度值与当代最优适应度值相除得到选择概率，进行选择。

将轮盘赌策略选择出的个体进行交叉、变异操作，将精英保留策略保留的个体直接插入交叉、变异之后的种群中，计算种群数量，如果数量小于种群规模N，则随机生成新个体，确保种群规模的一致性。

3.4 交叉操作

多点交叉可以避免过早收敛，但是过多的交叉点会影响优良基因的传承，本文权衡利弊后采用交叉点为2 的交叉操作。如图7 所示，交叉后找出单个个体中重复的点，对应父代X1、X2将个体非交叉区域中重复点替换为因交叉缺失的点，得到子代x1，x2。

图7 交叉操作示意图Fig.7 Schematic diagram of cross operation

3.5 模拟退火变异

需求点漂移影响应急救援路径的选择，单点变异较难跳出局部最优，故将模拟退火思想引入遗传变异操作，通过交换、逆转和插入的多策略变异方法对个体进行连续多次变异，并以Pt=exp的 概 率 接 受“ 劣 等 解”，ΔF=-fi如图8 所示，交换结构为随机选择染色体上的两个位置，然后将这两个位置上的元素进行交换；逆转结构为随机选择染色体上的两个位置，将两个位置之间的元素进行逆序排列；插入结构为随机选择染色体上的两个位置，将第1个位置后的元素插入到第2个元素的后面。

图8 染色体交换、逆转、插入操作示意图Fig.8 Schematic diagram of chromosome exchange,reversal and insertion operations

4 算例验证与结果分析

4.1 实例数据

本文基于2011 年蓬莱石油泄露事故的相关数据[7]开展实验。该事故的应急物资运输行动发生在事故发生6 h后。根据溢油实际信息得到溢油事故发生位置为离岸非特殊管理区域，则L=1 、M=1。根据渤海生态环境[16]，受影响动物栖息地的附加费用A*=10，溢油类型为中重油PC=4。经过测算，溢油造成的一大片油膜污染区域有30 个求援需求点需要围油栏进行围控。该事故溢油量为250 t，渤海海域水密度ρw为1.025 g·cm-3，渤海海域的风向为南风，海平面10 m的风速为10.6 kn，需求点受到两种洋流影响，分别是流速1.8 kn、流向东偏南37°漂移的洋流和流速为1.2 kn、流向为北偏西24°漂移的洋流。

各需求点的当前坐标、漂移速度和救援物资需求量等信息如表1所示。为方便计算，本文采用高斯投影法将经纬度坐标转换成为直角坐标。应急救援中心位置信息如表2 所示。船舶平均航行速度为15 m·s-1，船舶额定装载量为500 t，单位运输成本c1为450 元·km-1，固定运营成本c2为10000元·艘-1，权重因子a1和a2均取0.5。

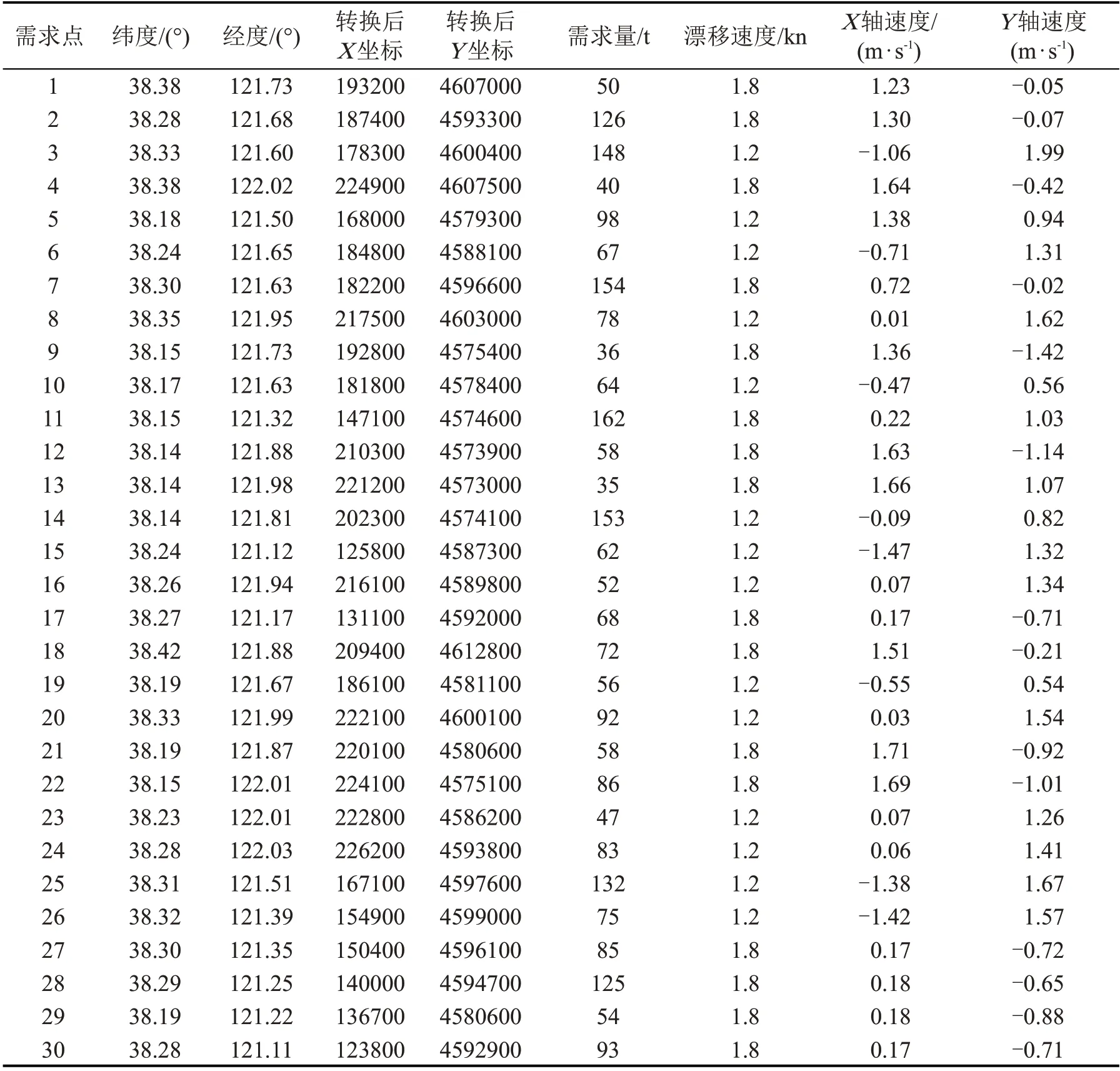
表1 救援物资需求点信息Table 1 Rescue material demand point information

表2 应急救援中心信息Table 2 Information of emergency rescue center

4.2 实例验证分析

本模型基于MATLAB R2021b 求解，在PC 端运行，操作系统为Window11，运行内存16 G，CPU为Inter(R)Core(TM)i5-10600kf，主频4.1 GHz。

在算法参数选择上，本文参照已有研究，采取逐个调整一个参数固定其他参数的方法，最终将参数确定为：种群规模N=50，最大迭代次数Gmax=400，交叉概率Pc=0.9，变异算子中交换结构概率Ps=0.2、逆转结构概率Pr=0.5、插入结构概率Pi=0.3，模拟退火初始温度Tsa=0.025，每次迭代冷却系数α=0.8，外层循环最大迭代次数=400，里层循环最大迭代次数=3。

为验证算法的有效性，引入传统遗传算法、模拟退火算法和参考文献[5]构建的改进粒子群算法与本文算法进行比较，算法收敛情况如图9 所示。模拟退火算法收敛缓慢，需要更多次迭代才能得到较好的解，遗传算法较容易陷入局部最优，改进粒子群算法虽然也能够获得较好的解，但较易陷入局部最优解，本文改进后的遗传模拟退火混合算法在保证收敛速度的前提下能够搜索到更优解。

图9 算法收敛性对比Fig.9 Comparison of algorithm convergence

本文算法获得的最优方案如表3所示，即同时派出6 艘救援船，其中大连基地3 艘、烟台2 艘、威海1 艘，具体救援路线如图10 所示，环境污染损失10199241.84 元，救援物资运输费用625251.89 元，整个溢油事故控制在约5384.68 km2的油膜污染面积内。此外，基于本文模型的求解实现了对救援点漂移位置的追踪，图11 为实施救援前后需求点位置差异。

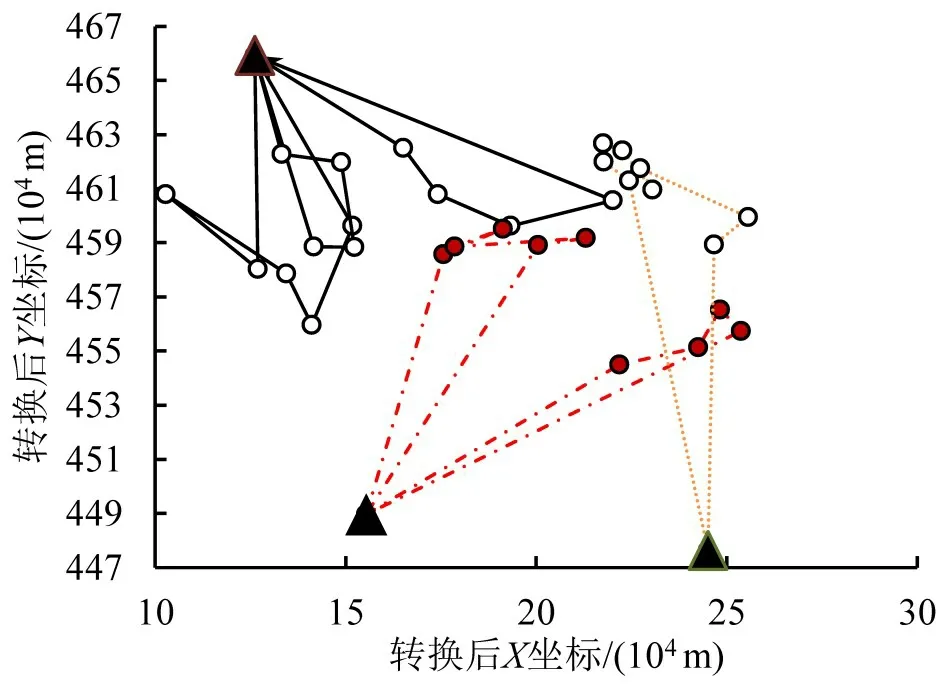
图10 最优救援方案路线图Fig.10 Roadmap of optimal rescue plan

图11 救援前后需求点位置示意图Fig.11 Schematic diagram of demand points before and after rescue

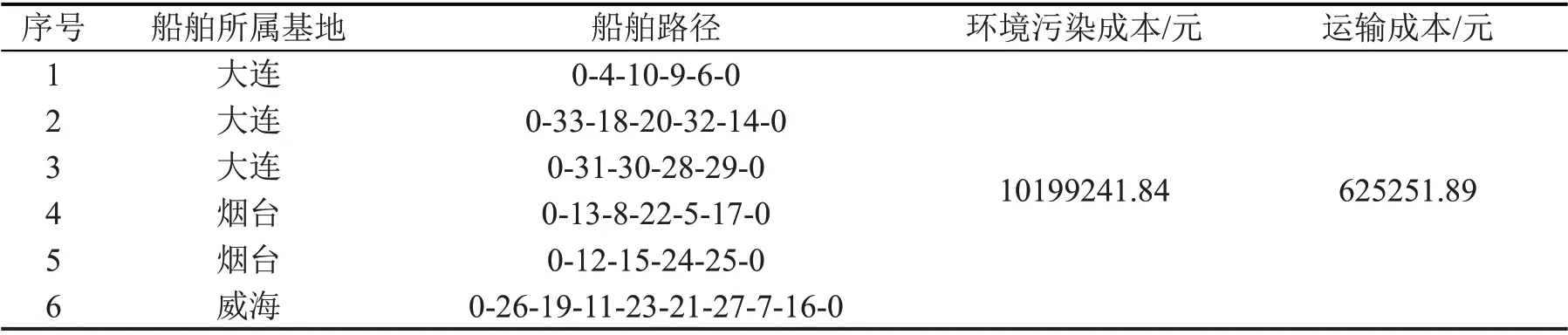
表3 应急救援配送方案Table 3 Emergency rescue distribution scheme

在此基础上，本文分析了制定应急救援方案时考虑需求点漂移的必要性。如表4所示，不考虑漂移得出的救援方案中所定位的需求点位置存在偏差，因此在实施时增加了额外的行驶距离，同时由于救援工作延误，导致油膜污染面积增加。与不考虑需求点漂移下获得的救援方案相比，本文方法在航行距离上减少了9.11%、环境污染降低了41.17%。

表4 考虑/不考虑需求点漂移因素的方案比较Table 4 Scheme comparison with/without demand point drift

4.3 数值实验分析

设计6组不同规模的算例，分别采取本文所提的混合算法和遗传算法、模拟退火算法进行求解。算例设计主要考虑以下因素：地理数据、船舶服务的需求点数量、需求点漂移扩散速度。地理数据依据Solomon实例数据集种R101、C101的数据，需求点在问题集R101中随机生成，而在问题集C101中采用聚类的方式产生。由于基准算例中没有漂移速度，本文为每个需求点随机生成-2＜vj＜2 的速度。对相同问题集分别取前25、50、100 个需求点构成小规模、中等规模和大规模的数据进行实验。

每次实验运行5次记录最大值、最小值和平均值，并通过计算每组算例中4种算法的目标值偏差来评估算法全局搜索能力和算法稳定性。如表5所示，本文算法与改进粒子群算法(IPSO)、模拟退火算法(SA)、遗传算法(GA)求解结果的平均偏差分别为1.63%、1.76%和20.39%。在小规模问题中，本文算法、IPSO 和SA 都可获得最优解，随着规模增大，本文算法的优越性凸显，在R101_100 算例中，IPSO、SA和GA的最优解与本文算法相比，分别增加了0.55%、1.41%和35.19%。算法稳定性上，在算例C101-25～R101-50 中，本文算法稳定性突出；在算例C101-100、R101-100中，本文算法与IPSO稳定性接近，优于SA和GA算法。综合比较，本文算法在保持稳定性的基础上在不同类型、不同规模的算例中具有更强的寻优能力。

表5 算法求解结果对比Table 5 Comparison of algorithm solution results

4.4 灵敏度分析

本文进一步分析了船舶容量、航行速度和需求点漂移速度等因素的影响。针对每个因素，分别在原数据基础上取-40%、-20%、20%、40%进行实验，实验结果如图12～图14所示。

由图12 可知：船舶容量增大可以有效降低运输成本，船舶容量减小时，船舶数量增加，频繁从应急救援中心派遣船舶直接导致船舶总运输成本增加；只要船舶数量充足，其容量的变化对油膜污染损失的影响并不明显。由图13 可知：当船舶航行速度加快时，船舶更快到达需求点，可以更有效地控制油膜污染面积，防止其扩散；由于本文算例基于渤海海域，溢油油膜实际是朝向海岸线扩散，因此出现船舶航行速度越快，救援越及时，反而需求点处在与陆地应急救援中心较远的位置，进而运输成本上升，所以单纯增加船舶航行速度对运输成本的影响不大。由图14可知：当需求点漂移速度增大时，油膜扩散加快，油膜污染面积明显增大；而漂移速度增大时，由于受到海上风浪的影响加剧，需求点之间的距离增加，进而增加了船舶总航行距离。

图12 船舶容量灵敏度分析Fig.12 Sensitivity analysis of ship capacity

图13 船舶航行速度灵敏度分析Fig.13 Sensitivity analysis of ship navigation speed

图14 需求点移动速度灵敏度分析Fig.14 Sensitivity analysis of moving speed of demand point

5 总结

(1)实例结果验证了海上溢油应急救援调度问题中考虑需求点漂移的重要性。与不考虑需求点漂移获得的救援方案相比，本文方法在总航行距离上减少了9.11%，环境污染降低了41.17%。本文方法能够获得较优的调度方案，实现更准确高效的应急救援，使险情得到及时控制，减少环境污染损失。

(2)算例分析结果表明：本文算法与IPSO、SA、GA算法求解结果的平均偏差分别为1.63%、1.76%和20.39%。在小规模问题中，本文算法、IPSO 和SA都可获得最优解，随着规模增大，本文算法的优越性凸显，在R101_100 算例中，IPSO、SA 和GA 的最优解与本文算法相比，分别增加了0.55%、1.41%和35.19%。在算法稳定性上，在算例C101-25～R101-50中本文算法稳定性突出，在算例C101-100、R101-100 中本文算法与IPSO 稳定性接近，优于SA 和GA 算法。综合比较，本文算法在保持稳定性的基础上在不同类型、不同规模的算例中具有更强的寻优能力。

(3)船舶容量对运输成本的影响更灵敏，而对油膜污染面积影响不明显。船舶航行速度对油膜污染面积影响更灵敏，而对运输成本的影响较小。因此，提升船舶容量可以明显降低应急救援运输成本，提升船舶航行速度可以更好地降低环境污染。