海底输油管道溢油输移扩散特性

朱耘志，杨宏伟

（中国南水北调集团中线有限公司，北京 100032）

在能源需求的驱动下，石油开采技术随之发展与进步，石油资源的开采逐步由陆地转向海洋，其中，在海洋油气开发中，采用管道运输是最为高效开采手段。然而，对于海底输油管道而言，复杂多变的海洋环境无疑带来了前所未有的挑战，全球范围内的海底输油管道溢油事故时有发生。因此，进行海底输油管道溢油输移扩散特性研究对海洋油气开发事故处理具有重要意义。

目前关于海底输油管溢油扩散的研究：马孜豪等研究了溢油孔径、洋流速度及泄漏速度对海底输油管道柴油泄漏的扩散特性的影响，结果表明洋流速度影响泄漏扩散的主要因素；Lalith K.Dasanayaka 等对具有羽流运动阶段和平流扩散阶段的模型和只有平流扩散阶段的简化模型进行了比较； Lindo-Atichati,D研究了溢油油滴尺寸、溢油速率、高压生物降解和垂直海水流速等对溢油输移的影响；Zhu 等对海底管道溢油扩散进行数值模拟，预测了海底溢油到达海面的时间及最大迁移距离。

综上可以发现：目前国内外关于水下溢油研究已经取得大量研究成果，但水深对泄露输移扩散的影响多见于天然气管路泄露，且以往研究中多没有考虑油气泄露一段时间后，溢油管段两端的阀门被关闭对溢油速度的影响。本文将采用Euler-Euler 双流体模型对海底输油管道泄露过程进行数值模拟，主要探讨海水流速、溢油密度、溢油初速度及水深因素对溢油输移扩散距离的影响。本文所做研究成果可为溢油事故处置方案的制定提供理论指导依据。

1 数值模拟过程

1.1 数值模型

连续方程

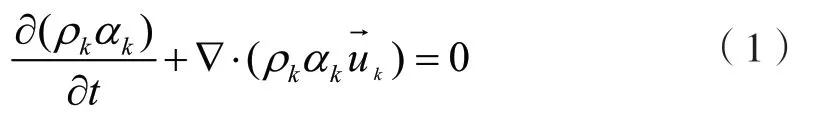
动量方程

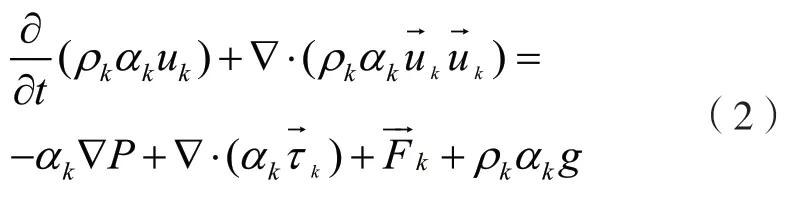
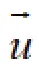
1.2 计算模型

根据工程实际建立数值计算几何模型如图1所示，其中，y 轴对称的二维矩形，其水平方向的长度随水深进行调整，为 60 m 或 80 m；泄漏口位于底边长度的四等分点处，且D=0.06 m。

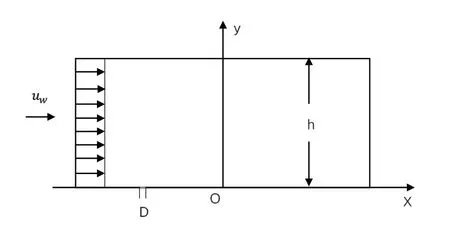
图1 几何模型

对几何模型进行网格划分，并对泄漏口处进行局部加密如图2所示，最终划分网格数量为 252778。

图2 网格局部加密

设置模型左侧为洋流速度入口，速度为0.05- 0.25 m/s；右侧为自由出流边界条件；D 处泄漏口为速度入口边界条件，并考虑溢油泄露后关闭阀门进行应急处置，使得溢油速率非均匀且随时间变化，适当简化后可得溢油速率随时间变化曲线如图3所示，溢油速度通过UDF 进行定义。

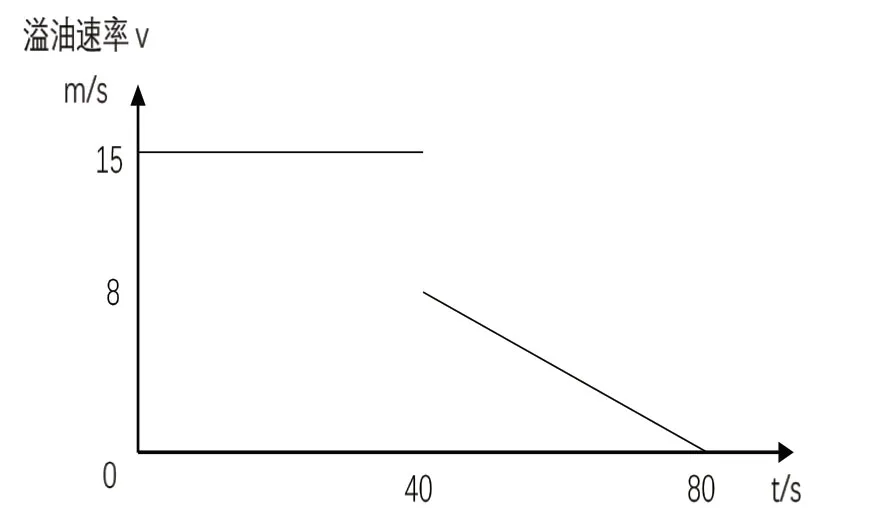
图3 溢油速度随时间变化曲线

2 结果分析

如图4所示为溢油输移扩散过程图，由图可见：t=3s 时，溢油的主干部分几乎垂直于海底平面，t=15s 时，溢油主干部分的倾斜程度越来越大，溢流顶部明显可见漩涡状流形，t=40s 时，溢流抵达水面，并沿水流方向扩散，t=46s 时，由于阀门关闭，泄露速率降低，溢流主干处出现断裂。

图4 溢油扩散过程

2.1 海水流速的影响

如图5所示，当溢油密度为780 kg/m，溢流初速度为15m/s，水深为20 m 时，由于海水流速的增大，使得溢流在水平方向上的速度显著增大，相同时间内，溢流在水平方向输移扩散的距离也就越远。故随着海水流速的增大，石油到达水平面后沿着海水方向的输移扩散距离也随之增大。

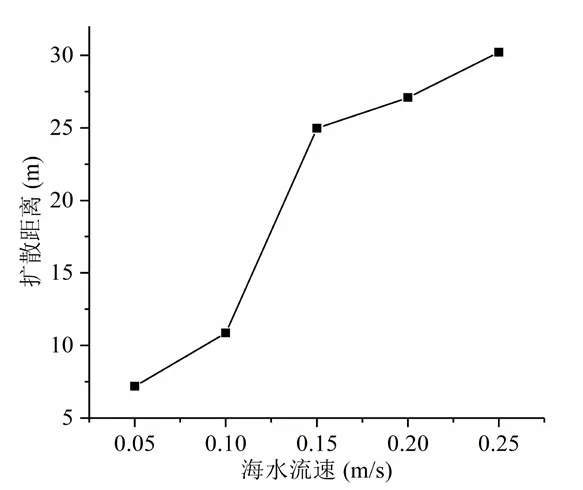
图5 溢油扩散距离随海水流速的变化曲线

2.2 溢油密度的影响

图6给出了海水流速为0.1 m/s，溢流初速度为15m/s，水深为20 m 时，溢油扩散距离随溢油密度的变化曲线，由图可知：随着溢油密度的增大，溢油在水面上的扩散距离随之减小，这是由于溢油密度越大，溢油扩散输移所需的推动力越大，故海水流速不变的条件下，输移扩散的距离越小。

图6 溢油扩散距离随溢油密度的变化曲线

2.3 溢油初速度的影响

图7给出了海水流速为0.1 m/s，溢油密度为780 kg/m，水深为20 m 时，溢油扩散距离随溢油初速度的变化曲线。由图可知：由于溢流初速度越大，溢油所具有的初始动量就越大，油品到达水面所需的时间就越短，横向水流对油品作用的时间就越短，从而使得油品沿海水方向的输移扩散距离越短，故随着溢油初速度的增大，溢油输移扩散的距离随之减小。

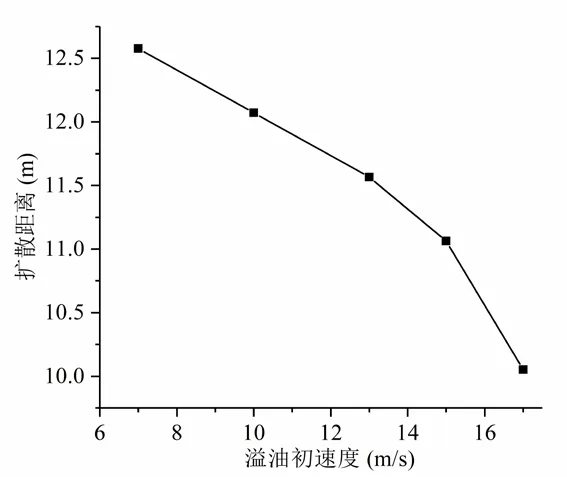
图7 溢油扩散距离随溢油初速度的变化曲线

2.4 水深的影响

图8所示为海水流速为0.1 m/s，溢油密度为780 kg/m，溢流初速度为15m/s 时，溢油扩散距离随水深的变化曲线。由图可见：当水深小于35m 时，随着水深的增大，溢油输移扩散距离呈缓慢增大，而当水深大于35m 时，输移扩散距离急剧增大。这是由于水深增大使得溢油到达水面的时间延长，海水作用时间更长，溢油扩散距离越远，当水深足够深时，由图8可知，溢油时间超过40s 后，溢油初始速度大幅降低，溢流所受到的推动能也大幅降低，进一步增大溢油到达水面的时间，这也使得输移扩散距离进一步增大。

图8 溢油扩散距离随水深的变化曲线

3 结论

本文对不同工况下海底输油管道溢油扩散过程进行数值模拟，并探讨海水流速、溢油密度、溢油初速度以及水深因素对溢油输移扩散距离影响行为。结论如下：

海水流速、溢油密度、溢油初速度以及水深均会影响溢油扩散距离，其中，海水流速的影响尤为显著。此外，海水流速越大、溢油的密度越小、溢油初速度越小、水深越深，溢油输移扩散距离越大。