改进的扰动LPV系统输出反馈预测控制

王 平，赵 敏

(上海理工大学 光电信息与计算机工程学院，上海 200093)

模型预测控制因其适用于处理约束和多变量问题而备受工业界青睐，是一种重要的控制技术[1-2]。文献[3]针对多面体描述的线性时变系统和线性时不变系统，提出了基于显式模型的鲁棒约束预测控制算法。文献[4]将这种思想应用于线性变参数系统，在假设系统状态精确可测的前提下，采用了一种基于拟最小最大算法的状态反馈预测控制方案。然而预测控制是基于模型的控制策略，精确的系统模型起着重要的作用，模型的不确定性在实际系统中是不可避免的，因此基于不确定模型鲁棒控制器的设计已成为一个重要的研究方向[5]。

为解决这一问题，文献[6～8]针对带有输入约束的LPV(Linear Parameter Variable)系统，采用了一种基于输出反馈的MPC(Model Predictive Control)方法。该MPC方法在线设计鲁棒状态观测器，基于状态观测器在线获得系统每一时刻状态的估计值，通过设计鲁棒输出反馈控制器得到最优控制律，保证了受输入约束系统的鲁棒稳定性。文献[9～12]采用一种基于拟最小最大算法的输出反馈鲁棒预测控制策略，基于线性矩阵不等式设计离线鲁棒状态观测器，利用鲁棒状态观测器观测系统状态，进而在线通过鲁棒输出反馈预测控制算法，得到最优控制律。虽然该算法考虑了LPV系统的不确定因素，但是难以保证受扰动系统的渐近稳定性。因此，本文将给出一种新的输出反馈预测控制方法来解决这一问题。

针对一类带有有界状态干扰的多胞描述LPV系统，本文以保证系统的渐近稳定性为目标，提出一种鲁棒预测控制改进方法，并设计了输出反馈控制器。该控制器考虑了无扰动LPV模型，基于线性矩阵不等式求解最小最大鲁棒输出反馈控制律；随后，获得保证扰动LPV系统鲁棒渐近稳定的最优偏移量，与无扰动系统反馈控制律组合得到最优控制律，并施加于实际系统；最后，证明了扰动LPV系统的渐近稳定性。

1 问题描述

考虑以下不确定LPV系统

xc(k+1)=A(ρ(k))xc(k)+B(ρ(k))uc(k)+w(k)

yc(k)=C(ρ(k))xc(k)

(1)

式中，uc(k)∈Rnu、xc(k)∈Rnx、yc(k)∈Rny分别为系统的控制输入、不可测状态以及可测输出；w(k)⊂W为有界干扰，且W⊂Rnx；A(ρ(k))、B(ρ(k))、C(ρ(k))属于多面体矩阵集合

[A(ρ(k))|B(ρ(k))|C(ρ(k))]∈Ω

(2)

其中

Ω=Co{[A1|B1|C1]，[A2|B2|C2]，…，[Al|Bl|Cl]}

(3)

式中，Co为凸包；{[A1|B1|C1]，[A2|B2|C2]，…，[Al|Bl|Cl]}，j∈{1,2,…,l}为多面体Ω的顶点；l为多面体顶点的个数。

假设1ρ(k)在k时刻可测量，即[A(ρ(k))，B(ρ(k))，C(ρ(k))]在k时刻已知。

假设2(A(ρk))，B(ρ(k)))以及(C(ρ(k))，A(ρ(k)))，对于所有k≥0为完全可控可观。

本文针对如式(1)所示的带有有界状态干扰的不确定LPV系统，设计输出反馈鲁棒预测控制器，得到最优控制律，并施加于该系统，保证了扰动LPV系统的鲁棒渐近稳定性。

2 无扰动LPV系统控制器设计

考虑无扰动LPV系统模型如式(4)所示。

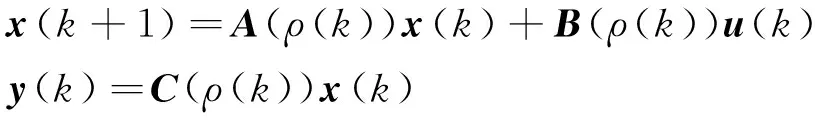
(4)

为求取控制律使如式(4)所示的系统渐近稳定，首先提出一种鲁棒状态观测器的离线设计方法；进而构造具有LMI(Linear Matrix Inequality)约束的在线优化MPC问题；最后通过求解该优化问题得到最小最大鲁棒输出反馈控制律。

2.1 离线状态观测器设计

由于如式(4)所示的系统状态不可测，故采取如下所示的状态观测器[13]

x0(k+1)=A(ρ(k))x0(k)+B(ρ(k))u(k)+

Lpy(k)-C(ρ(k))x0(k))

(5)

式中，x0(k)、u(k)、y(k)分别为估计状态、控制输入以及可测输出。为确定观测器增益Lp，定义该系统的估计误差e(k)=x(k)-x0(k)，则下一时刻

e(k+1)=(A(ρ(k))-LpC(ρ(k)))e(k)

(6)

定义一个二次函数

(7)

且满足二次稳定性条件

E(e(k+1))-μE(e(k))≤0

(8)

式中，μ(0<μ<1)是预先指定的衰减率，可保证当k→∞时，e(k)→0。将式(6)和(7)代入(8)中，且左右分别乘以对角矩阵{I，Pe}，令Ye=LpPe，可得

(9)

通过求解以下优化问题可得Lp。

(10)

2.2 在线输出反馈预测控制

为保证式(4)的渐近稳定性，引入以下预测模型[14]

g(k+1+i|k)=A(ρ(k+i))g(k+i|k)+

B(ρ(k+i))u(k+i|k)

(11)

g(k+1|k)=x0(k+1)

式中，i≥1；g(k+i|k)，u(k+i|k)分别为式(4)在k时刻预测k+i时刻的系统状态以及控制输入。令g(k|k)=x0(k)，u(k)=u(k|k)，未来控制律描述为

u(k+i|k)=F(k)g(k+i|k)

(12)

式中，F(k)为k时刻确定的反馈增益。

针对式(4)在每个时刻求解如下最小最大优化问题

(13)

式中

(14)

同时二次函数V(g(k+i|k))满足以下约束条件[15]

(15)

由鲁棒稳定性可得g(∞|k)=0，即V(g(∞|k))=0，将式(15)左右两端从i=1到∞分别相加可得

(16)

式中

V(g(k+1|k))=g(k+1|k)TP(k)g(k+1|k)

(17)

对系统性能附加约束

(18)

其中γ(k)是待最小化的非负变量。

基于式(15)、式(18)，可将所提出的最小最大优化问题修改为

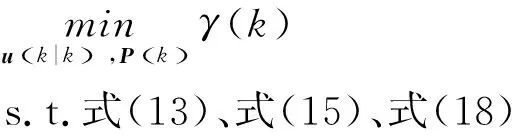
(19)

为保证式(19)的鲁棒稳定性，附加如下所示的稳定性条件。

γ(k)<γ(k-1)

(20)

在满足式(15)、(20)，式(18)的条件下，解决式(19)可得控制律u(k)及反馈增益F(k)，因此，设计上述鲁棒控制器的问题可转化为一个带有LMI约束的优化问题，如下定理所示。

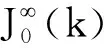
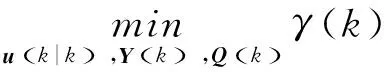
(21)

s.t.式(4)、式(5)、式(13)

(22)

(23)

γ(k)-γ(k-1)<0

(24)

式中

(25)

若对于给定的x0(k)和y(k)存在u(k|k)、Y(k)、Q(k)，则反馈增益F(k)可由F(k)=Y(k)Q(k)-1计算得到。

证明将式(18)中P(k)替换为γ(k)Q(k)-1可得

1-Ψ(k)-T(k)TQ(k)-1T(k)>0

(26)

式中

(27)

通过应用Schur补定理，可得

(28)

式中

(29)

同理对式(28)应用Schur补定理，由此可得式(22)，因此式(18)可由式(22)保证。

令u(k+i|k)=F(k)g(k+i|k) (i≥1)，将式(12)代入式(15)，可得

ζ(k)-ξ(k+i)TP(k)ξ(k+i)>0

(30)

其中

(31)

式(30)两边分别乘以γ(k)P(k)-1，令P(k)=γ(k)Q(k)-1且应用Schur补定理可得到

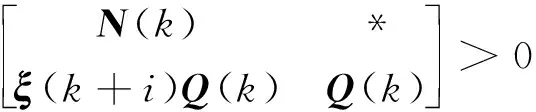
(32)

式中

(33)

令Y(k)=F(k)Q(k)后应用Schur补定理可得

(34)

式中

R(k)=A(ρ(k+i))Q(k)+B(ρ(k+i))Y(k)

(35)

将不等式(34)映射于式(36)中

[A(ρ(k+i))|B(ρ(k+i))|C(ρ(k+i))]∈Ω

(36)

若存在Q(k)和Y(k)使式(34)成立，则可证得式(23)成立，因此式(15)可由式(23)保证，此时证毕。

定理2(递归可行性) 对于式(21)，若k时刻能确定一个递归可行解，则在所有t>k时刻，式(21)都是有解的。

证明若证明k时刻得到的优化问题的解是k+1时刻的可行解。设

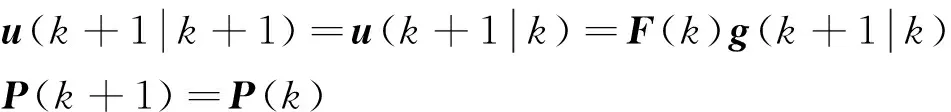
(37)

基于式(5)、式(11)、式(24)及式(37)，则式(22)和式(24)可被改写为

(38)

式中

(39)

由于式(23)在k时刻被满足，所以式(38)成立，因此若能在k时刻确定一个可行解，则式(21)在k+1时刻可行；证毕。

定理3(渐近稳定性) 式(21)的可行解保证系统的渐近稳定性，即当k→∞时，x(k)→0。

证明若式(21)对于所有步骤可行，基于式(15)的式(24)保证g(k+1|k)收敛到0，此外从状态观测器的设计中可保证当k→∞时，e(k)→0，即估计状态x0(k)收敛于式(4)真实状态x(k)，因此式(21)的可行解保证系统的渐近稳定性，即k→∞时，x(k)→0，此时证毕。

综上所述，本文针对无扰动系统模型提出的在线优化MPC问题描述如下

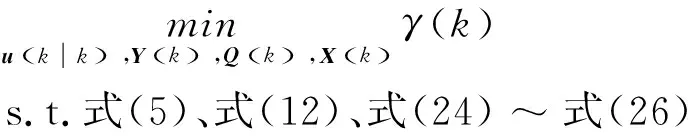
(40)

通过求解式(40)可获得基于输出反馈的鲁棒预测控制律u(k+i|k)，保证无扰动LPV系统的渐近稳定性，下面则考虑在有界状态干扰的情况下，如何求取最优控制律。

3 扰动LPV系统最优控制律

考虑扰动LPV系统，由于式(1)状态xc(k)不可测，采取如下所示的状态观测器

xc0k+1)=Aρk))xc0k)+Bρk))uk)+

Lpyk)-Cρk))xc0k))

(41)

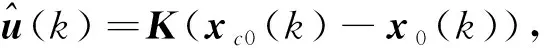
uck)=uk)+Kxc0k)-x0k))

(42)

由式(42)可得，xc0(k)与x0(k)的差值可分别基于式(41)、式(5)得到，u(k)可通过求解式(40)得到，而反馈增益K未确定，故下面通过状态反馈确定反馈增益K，根据式(5)、式(41)定义z(k)=xc0(k)-x0(k)为控制误差，则下一时刻控制误差

(43)

式中，ec(k)、e(k)分别为式(1)、式(4)的估计误差，基于上述离线状态观测器的设计可得，当k→∞时，ec(k) →0，e(k) →0。因此为使式(43)稳定，(A(ρ(k))+B(ρ(k))K)一定趋于0，根据式(43)可得[16]

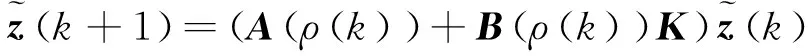
(44)

定义二次函数

(45)

并满足以下二次稳定性条件

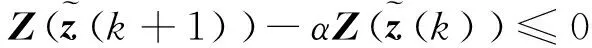
(46)

其中，α(0<α<1)是预先指定的衰减率，将式(44)、式(45)代入式(46)中可得

(47)

将式(47)左右分别乘以{I，Pz}，并令Yz=LpPz，有

(48)

故求取下列优化问题即可确定反馈增益K。

(49)

最后根据式(42)可得最优控制律uc(k)。

定理4最优控制律uc(k)施加于扰动LPV式(1)中，保证了扰动LPV系统的鲁棒渐近稳定性。

证明状态反馈增益K可保证当k→∞时，(A(ρ(k))+B(ρ(k))K)→0，且当k→∞时，ec(k)→0，e(k)→0，因此由式(43)可得，当k→∞时，控制误差z(k)趋于0，所以xc0(k)最终会收敛到x0(k)。无扰动控制律的设计保证式(4)的渐近稳定性，即当k→∞时，x0(k) →0，因此当k→∞时，xc0(k) →0；又因为当k→∞时，ec(k) →0，所以式(1)的估计状态xc0(k)将会收敛到式(1)的实际状态xc(k)，即当k→∞时，xc(k)→0；由此可得将最优控制律uc(k)施加于式(1)中，保证式(1)的鲁棒渐近稳定性；证毕。

当系统的初始状态在某一输入的驱动下，系统从这一初始状态运动到末态，若存在扰动使系统的初始状态在某一范围内发生偏移，但系统的终态仍能回到给定的末态范围内，则称该系统是稳定的，这就是普通意义上的稳定性。而渐近稳定性是稳定性的一种，它要求当时间趋于无穷时，当系统的初始状态在某一范围内，系统的终态会回到零点。可见渐近稳定比稳定对系统的要求严格，前者只需系统末态所在的范围是零点周围的一个区域，而后者要求系统末态趋近的这一点必须是零点，这就是渐近稳定性与稳定性的区别。通过上述定理4的证明，说明本文所提出的方法控制性能较好，能够保证扰动LPV系统的渐近稳定性。算法具体步骤如下文所述。

离线阶段步骤：

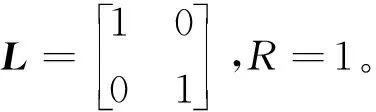
步骤1计算Lp、K；选择合适的L和R；

步骤2选择合适的衰减律μ(0<μ<1)、α(0<α<1)使得式(10)、式(49)可行。

在线阶段(k≥0)步骤：

步骤1在k= 0时刻，分别选定式(4)、式(5)的初始状态x(0)、x0(0)；

步骤2在k≥0时刻，根据式(5)得到x0(k)，根据式(41)得到xc0(k)，并计算xc0(k)-x0(k)；

步骤3基于式(5)在线求解式(40)获得控制输入u(k)以及反馈增益F(k)；

步骤4计算uc(k)=u(k)+K(xc0(k)-x0(k))，并将uc(k)施加于实际系统中；

步骤5重复在线阶段的步骤2，直至xc0(k)=0，结束。

4 数值例子

通过下面的数值算例证明该方法的有效性，首先给出如下所示的LPV系统

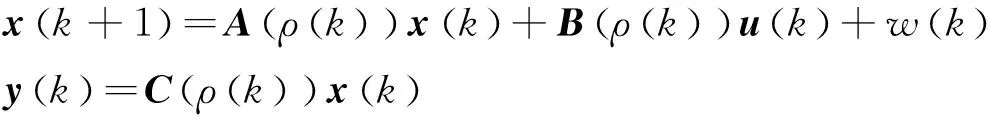
(50)

引用模型系数[17]

(51)

给式(50)加入有界扰动w(k)∈W

W={w∈R2||w|∞≤0.01}

根据反馈增益K、式(5)以及式(41)每一时刻所估计的状态值可得到每一时刻的扰动LPV系统控制输入的偏移量，随后在线求解式(40)得到无扰动系统控制输入u(k)，最后将无扰动控制律组合最优偏移量得到式(50)的最优控制律u*(k)。下面将对文献[10]中的方法与本文中的方法做对比分析。

由图1可以看出，文献[10]所提出的方法能够保证扰动LPV系统的末态进入零点周围的一个区域，但是难以保证扰动LPV系统的渐近稳定性；而本文所提出的方法可使得扰动LPV系统状态更快地进入稳态，并且能够保证扰动LPV系统的渐近稳定性，因此本文所提出的方法要优于文献[10]。本文中，在MPC的设计中考虑到了有界状态干扰所造成的偏移量，因此相比于未考虑扰动的MPC方法[18]，本文所提出的方法在实际生活中更加具有通用性。存在干扰的式(50)估计状态与实际状态的横、纵坐标分别绘制在图2、图3中，估计状态轨迹的坐标设定从[-0.8，-0.2]开始，实际状态轨迹坐标设定从[-1，1.2]开始，图2以估计状态与实际状态的横坐标为y轴，以时间为x轴。

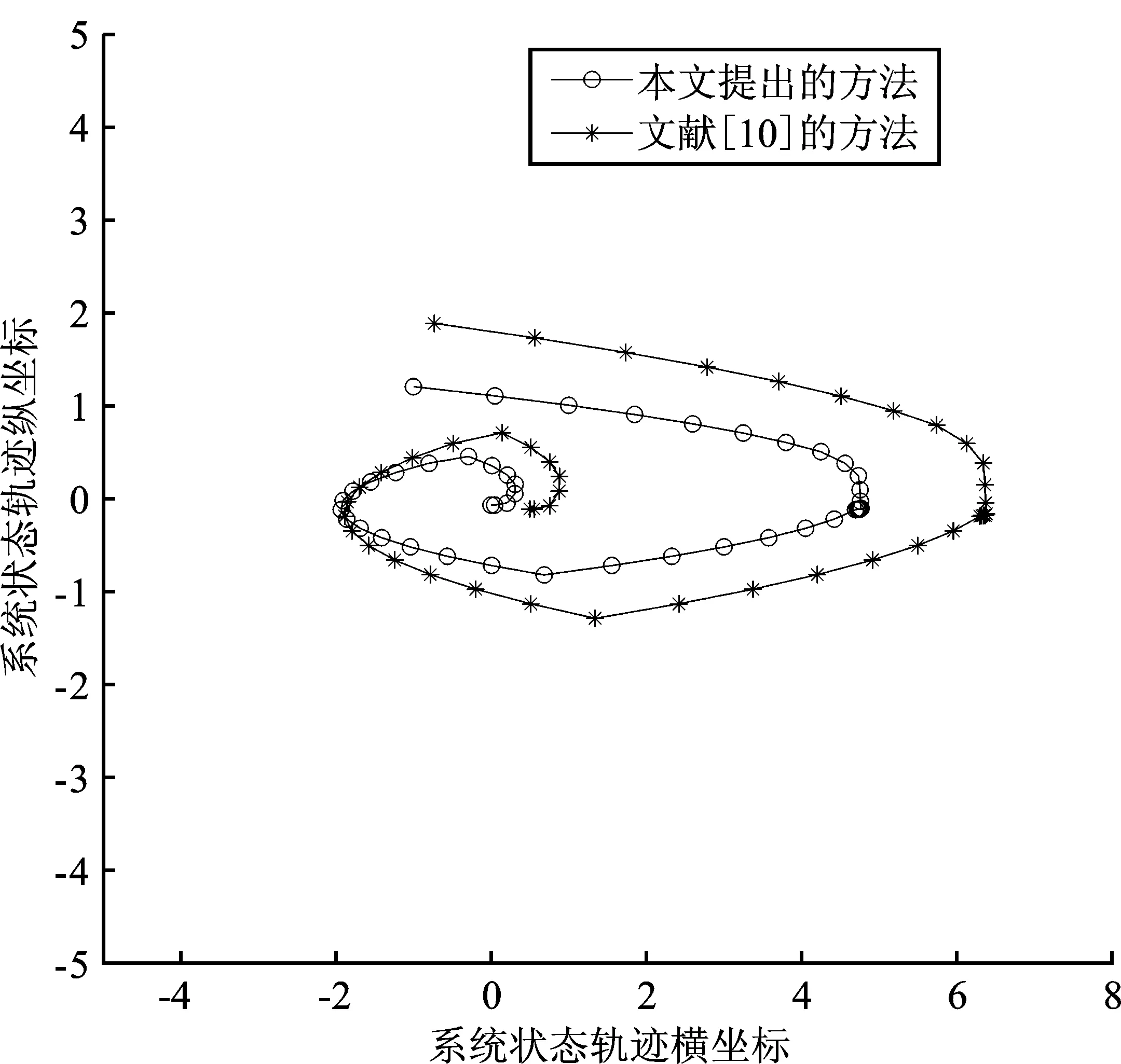
图1 系统状态轨迹对比图Figure 1. Comparison diagram of system state trajectories

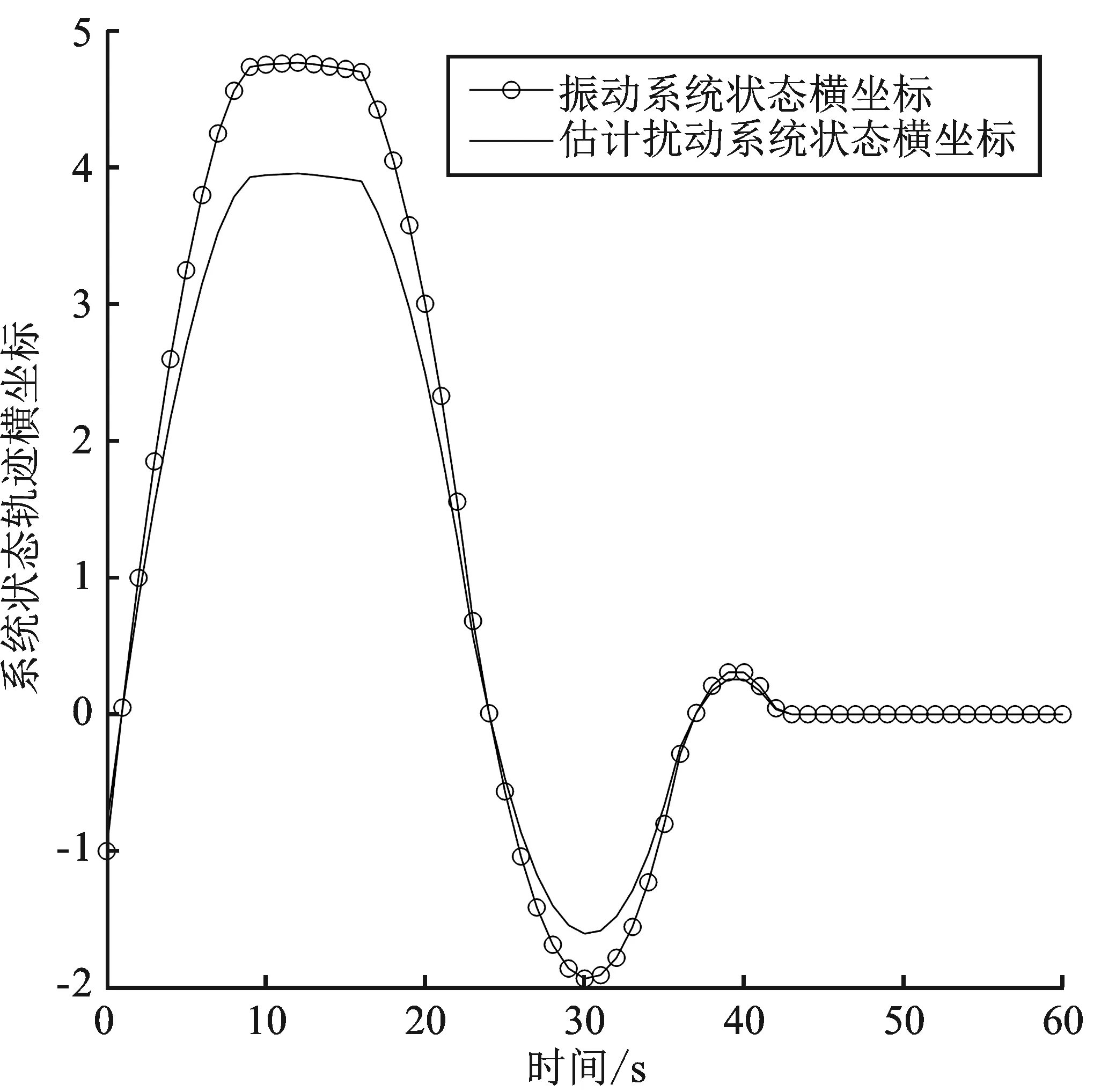
图2 估计状态与实际状态横坐标轨迹Figure 2. Estimated and actual state abscissa trajectories

图3以估计状态与实际状态的纵坐标为y轴，以时间为x轴。

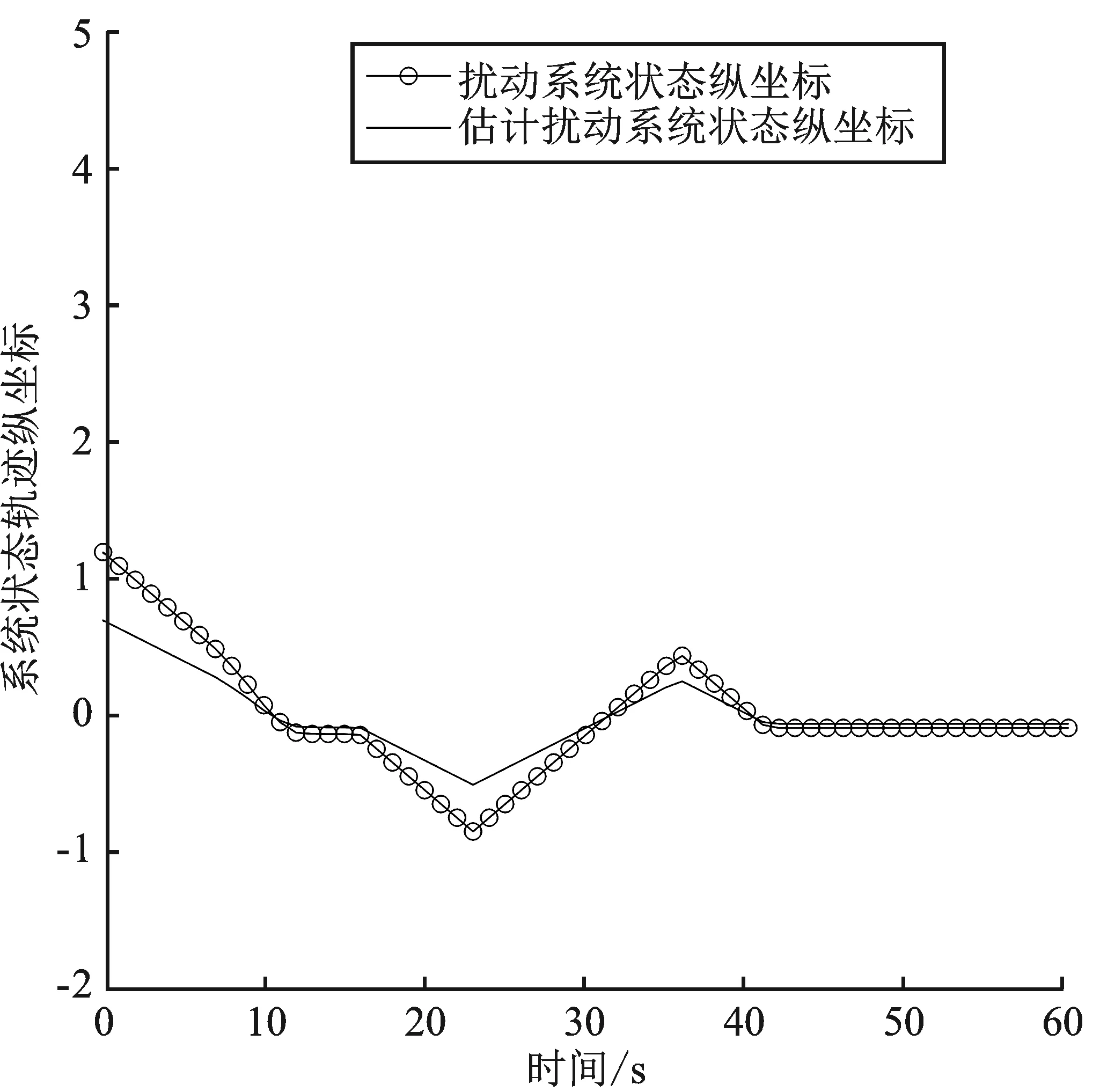
图3 估计状态与实际状态的纵坐标轨迹Figure 3. Estimated and actual state longitudinal trajectories

由图2、图3可以看出，式(50)估计状态与实际状态的坐标轨迹最终汇合并且收敛于0，所以表明本文所提出的状态观测器效果良好。系统的最优控制律如图4所示。

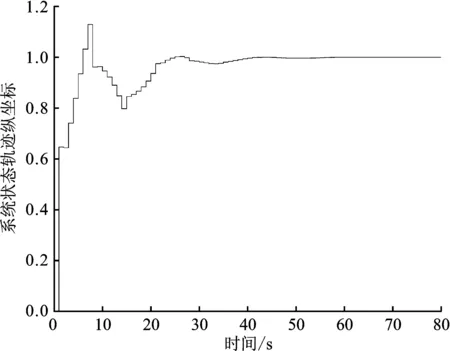
图4 扰动LPV系统的最优控制律Figure 4. Optimal control law for a perturbed LPV system

由图4可以看出，本文所提出的方法具有递归可行性，每一时刻都可求得最优控制律。该仿真针对二维系统，只有两个变量，当变量个数增加后，系统维数增加，若采用本文方法，计算量会增大，因为相对应的矩阵维数会随之增加，因此基于线性矩阵不等式的在线优化问题的求解，离线状态观测器增益以及反馈增益K的确定都更加繁琐。对于高维数系统的渐近稳定性而言，定理4同样适用于高维数系统，因此当系统维数增高，本文所提出的方法同样可保证系统的渐近稳定性。

5 结束语

本文针对一类带有有界状态干扰的多胞描述LPV系统，提出了一种改进鲁棒预测控制方法，设计了可保证系统渐近稳定的输出反馈控制器。该控制器考虑无扰动LPV系统模型，基于LMI约束求解输出反馈控制律。为抵消有界状态干扰，本文设计并求取扰动LPV系统控制输入的最优偏移量，基于无扰动系统模型求取的控制律组合最优偏移量即可得到扰动LPV系统的最优控制律，最后将最优控制律施加到实际系统中，并通过仿真实验验证了算法的有效性。