RTEthernet中改进的FTA时钟同步算法研究
张宇辉,张凤登,张海涛
(上海理工大学 光电信息与计算机工程学院,上海 200093)
RTEthernet(Real-Time Ethernet)是新提出的一种实时以太网,该网络能够兼容传统以太网的实时以太网协议,主要应用于工业、车载以太网技术应用。这种实时以太网采用总线拓扑结构,在传统的物理层和数据链路层之上增加了会话层,并使用 “通信循环”的概念分时传输实时性消息和非实时性消息。
对于时钟同步技术的研究,国外在该领域的起步较早。1978年,文献[1]较为全面地阐述了时钟同步技术的原理、方法以及时钟同步在分布式系统中的应用。文献[2]以经典的Lamport时钟同步算法为基础研究了平均值算法和Berkeley算法,且这两种类型算法的核心都是平均技术。文献[3]针对确定全网时钟的问题提出了一种基于平均场的分布式时钟同步方法,该算法将节点间的时钟偏差映射为团势能,然后使用能量函数来描述时钟同步平均场模型。该方法中,时钟同步的核心思想仍基于平均场理论,通过节点间的平均作用来确定全网虚拟时钟基准。目前多数关于分布式时钟同步算法的研究都是针对某一网络进行适应性改进。基于此,本文通过对RTEthernet协议通信原理及其基础时钟同步算法的研究,考虑最恶劣的拜占庭故障对系统时钟精密度的影响,分析时钟同步的条件和经典时钟同步算法,即容错均值(Fault-Tolerant Average,FTA)算法,逐步提出容错性更高的时钟同步算法。
1 RTEthernet基本原理
RTEthernet是一种实时以太网,它保留了传统Ethernet的物理层和数据链路层工作模型,并在此基础上使用了ISO/OSI参考模型的第5层(会话层)进行报文的再封装。RTEthernet网络还引入了“全局时间”的概念,这使得其不仅可以兼容传统以太网,还可以使用时分多路访问(Time Division Multiple Access,TDMA)的通信方式进行基础报文的传输,从而克服了传统以太网在负载较高时延迟较大的影响,提高了传统以太网的实时性和安全性。
1.1 体系结构
国际标准化组织(International Organization for Standardization,ISO)制订的开放式系统互连(Open System Interconnection,OSI)参考模型共分7层,从低到高依次为物理层、数据链路层、网络层、传输层、会话层、表示层和应用层[4-5],如图1所示。
由图1可以看出,以太网只定义了ISO/OSI体系结构中的最低两层,这主要是因为物理层是用来建立实时传输网络中的物理连接,而数据链路层是用来将数据封装成帧进行传输,以此实现真的顺序控制、差错控制以及流控制等功能,使得不可靠的链路变成可靠的链路,这两者都是必不可少的部分。然而,RTEthernet要做的是在这两层的基础上添加一个协议层,且不改变Ethernet的物理层和数据链路层。为此,该协议修改了OSI/ISO参考模型的会话层。

图1 ISO/OSI、Ethernet和RTEthernet的体系结构Figure 1. Architecture for ISO/OSI、Ethernet and RTEthernet
1.2 工作原理
RTEthernet协议是以确定性定时通信为基础,其通信方法是基于周期性重复的通信循环,因此需要提前建立通信循环和时间窗口的大小。如图2所示,本文类比矩阵行和列的方式,将RTEthernet的整体情况进行展示。图中的矩阵从宏观上展现了RTEthernet的一般性工作原理。
图2形象地展示了RTEthernet的通信原理,其中每个通信循环中包含了静态段、动态段和网络空闲时间段。在实际实现中,循环的个数是一个常数,具体会根据实际应用的需求进行设定。在基本的通信循环中用于报文传输的时间只在动态段和静态段,并且所有要通过该网络进行传输的报文都会被组织成静态段或者动态段的元素。在静态段中进行传输的报文都是周期性的、具有实时性的报文,其元素所处的位置都是固定的,而动态段传输的是随机的、事件触发型报文,其中的元素位置是不固定的。因此,这种通信模式定义了时间窗口与使用该网络进行传输的报文的相关性。
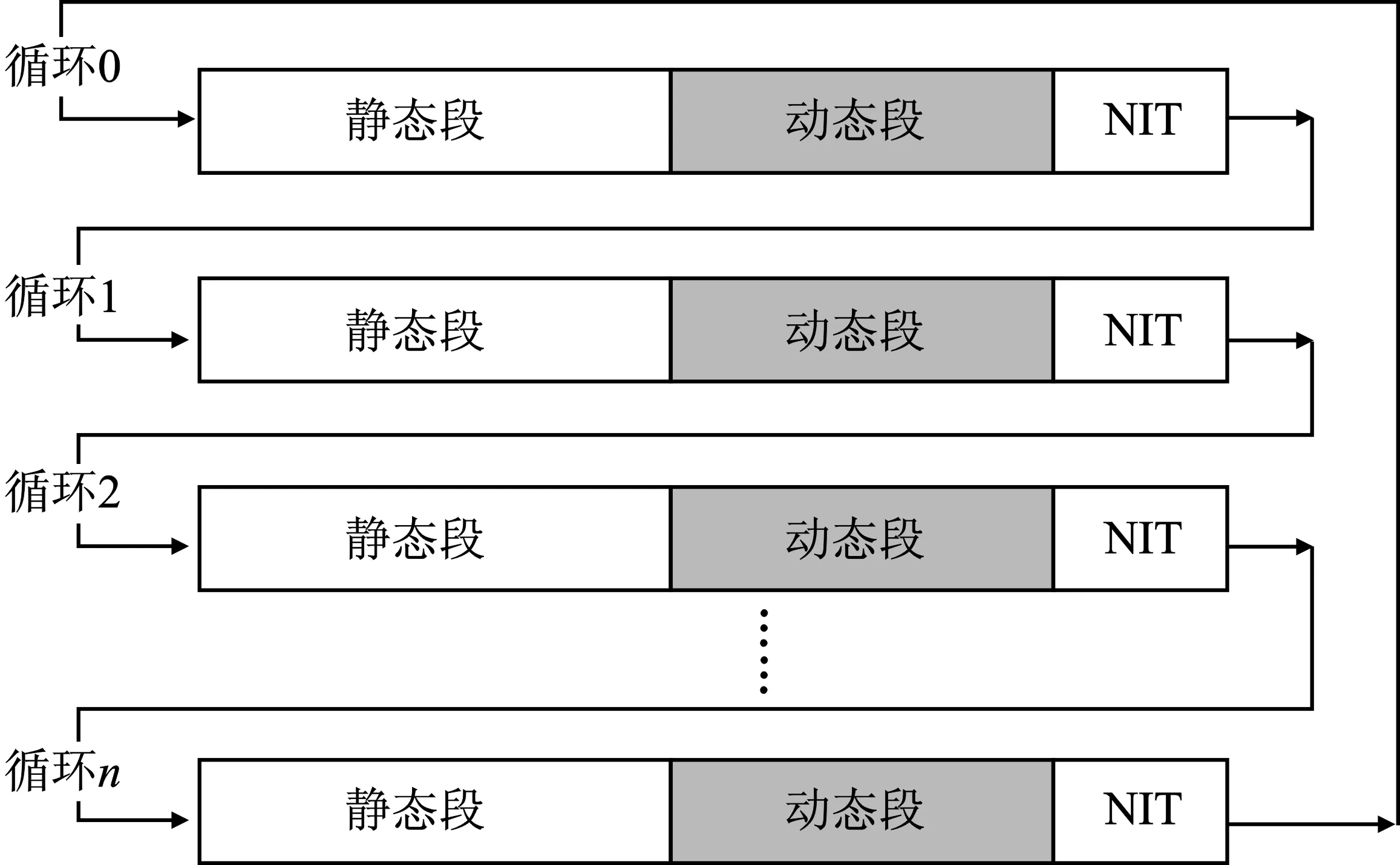
图2 RTEthernet通信原理Figure 2. RTEthernet communication principles
2 时钟同步
分布式系统[6]由一组处理器组成,它们通过消息交换进行通信,并且不能访问全局时钟。尽管如此,越来越多的分布式应用程序,例如过程控制应用程序、事务处理应用程序或通信协议,都要求同步时钟能够拥有近似相同的时间视图。在此上下文中,时间意味着实际时间的近似值或简单的整数值计数器。确保物理上分散的处理器有共同的时间知识的算法被称为时钟同步算法。
2.1 误差来源及时钟故障分类
由于分布式系统中的各个节点对于时间的看法各不相同,因此需要对其进行时钟同步。造成这一现象的主要因素是温度和老化,这使得各个节点的硬件时钟的晶振频率发生漂移。在实际应用中,漂移率的量级通常在10-6s[7]。
在分布式系统中,节点的故障可以定义为不符合正常行为的表现。节点中的所有组件,例如处理器、时钟、通信的链路等都可能出现故障。对于各个节点的时钟而言,与其相关的故障主要分为7类[8]:其中最著名的是时钟拜占庭故障[9](Clock Byzantine Failure)。
在分布式系统中,任意节点都可能会存在上述类型的某一种故障或几种故障混合,在这种情况下则称该节点是故障的,否则是无故障的。同时,在本文主要考虑的就是最恶劣情况(拜占庭故障,如图3所示)下的两种情况。如果一个时钟同步算法能够使得分布式系统能够容忍上述最恶劣情况下的故障,则表明该算法是有效的。因此,时钟同步算法容错性的重点就体现在系统对拜占庭故障节点的容忍性上。

图3 时钟拜占庭故障Figure 3. The clock Byzantine failure
2.2 时钟同步的基本表征
为了能够有效衡量系统中各个时钟是否达到同步,本文引入了如下衡量指标:时钟偏差Δ(Offset)、精密度φ(Precision)和准确度ψ(Accuracy)。
偏差Δ为具有相同粒度的两个时钟在同一单位微节拍上的偏差,可用下式表示
(1)
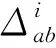
精密度φ为在给定的真实时间间隔[t1,t2]内,时钟集合{1,2,3,…,n}上任意两个时钟间的最大偏差,可用下式表示
(2)
式中,i表示微节拍;a、b表示时钟编号。一般情况下,有限时间间隔上的最大φi称为时钟集合的精密度。衡量一个系统内所有节点间的时钟是否达到同步就是根据精密度来判断的。若精密度小于某个期望值,则表示系统内部的各节点之间相互同步,反之,则未达到同步。
准确度ψ为任意时钟a相对于参考时钟r在微节拍i的偏差,用ψia表示
(3)

此外,时钟同步算法从不同的角度可以分为不同的类型,从宏观上可以将时钟同步算法分为外部时钟同步算法与内部时钟同步算法[10-12];从同步时使用的工具角度上可以将时钟同步算法分为硬件时钟同步算法与软件时钟同步算[13-15];从容错性的角度,又可以将时钟同步算法分为容错性算法和非容错性算法。
3 算法模型
3.1 系统模型假设
假设1(时钟偏移率有界) 存在一个很小的已知常数ρ,其中0<ρ≪1,本文定义一个无故障时钟Hi(t)在所有的真实时间t上都是ρ有界的,即该时钟满足如下特性
(4)
其中,Hk(t)表示节点k的本地时钟值;ρ表示本地硬件时钟的漂移率。
假设2(时钟初始同步) 设分布式实时系统在真实时间t0时刻开始启动,逻辑时钟初始是同步的,即对于某个固定值φint和系统内任意两个无故障节点p、q在t0时刻满足下式
|Cpt0)-Cqt0)|≤φint
(5)
式中,Cp(t0)、Cq(t0)分别表示时钟p、q在真实时间t0时刻的时钟值;φint表示无故障节点初始同步时两者之间的最大偏差。
假设3(故障节点数有界) 由文献[16]可知,当系统中故障节点数超过总节点数的1/3时,在不使用签名认证的技术下,将无法维持时钟同步。因此,假设参与时钟同步的节点总数为n,可能发生故障的最大节点数为f,则n和f满足式(6)。
n≥3f+1
(6)
RTEthernet定义了一个确定性的多主网络。为了使它的传输速率尽可能地靠近以太网,将RTEthernet系统的基本结构定义为星型拓扑结构。
当进行远程时钟读取和计算时,除故障的情况之外,还会有时间上的延迟。为了方便对下文时钟同步算法的描述和分析,本文对系统模型做如下假设。
假设4(传输延迟有界) 对于某些非负常数δ和ε,且δ>ε,每条报文的发送和接收对应真实时间的差值de存在一个已知的上下界,即
de∈[δ-ε,δ+ε]
(7)
式中,δ表示报文传输延迟范围的中值;ε表示读取其他节点时钟值时的读取误差。
除了假设传输延迟有界外,延迟的长短还与其他因素相关,例如任意一个节点Ni在分布式系统中接收到报文进行处理、运行算法所需的时间等。
假设5(算法执行时间) 本文假设这些时间都可忽略。在实际情况中,造成消息延迟的主要原因是传输延迟,而执行算法、处理报文等产生的延迟都远小于传输延迟,为简化起见,将忽略这些延迟。
假设6(重同步周期) 为了保证时钟同步,非故障节点p发送消息时,其余非故障节点q都与p处于同一轮次,因此要求重同步周期λ满足下列条件
λ>21+ρ)φint+ε)+1+ρ)max{δ,φint+ε}+ρδ
(8)
且
λ≤φint/4ρ-ε/ρ-ρφint+δ+ε)-2φint-δ-2ε
(9)
式中,δ为可能的消息延迟范围的中值;ε为消息延迟的不确定度;φint为常数,表示初始同步程度的上限。
3.2 时钟同步条件
根据章节3.1给出的系统模型,时钟同步算法需满足一定的同步判断条件才能证明算法的收敛性和有效性。
对于所有正确时钟Ci和Cj,如果在时间Ti+1之前,所有时钟中除了最多m个时钟之外都没有故障,那么时钟同步算法需满足以下时钟同步要求:
(1)R1(收敛性/精密度)。|Ci(t)-Cj(t)|≤φi,其中φi表示时钟同步算法的精密度;
(2)R2(校正项有界)。每次重新同步时,一个无故障时钟被改变的大小在数量上有一个小的限制。
4 FTA算法的分析及改进
目前国内外出现了较多的分布式实时系统时钟同步算法,其中容错均值(Fault-Tolerant Average,FTA)算法是一种最典型的时钟同步算法。
FTA算法是一种单轮算法,能够处理不一致信息,限制由不一致性引入的错误。该算法起源于传统的“平均技术”,引入去极值的思想,从而形成了基础的时钟同步算法,实现过程如图4所示。

图4 FTA算法同步过程Figure 4. The synchronization process of FTA algorithm
对于由N个节点组成的系统,要容忍x个拜占庭故障,每个节点通过交互的方式收集本地时钟与其他节点的时钟之间的时间偏差,得到N-1个时间偏差,加上自身的时间偏差,总共得到了N个时间偏差。然后,将这些时间偏差由大到小排序,去除偏差序列中x个最小值和x个最大值,最后对剩余序列中的N-2x个时间偏差求平均值,以此来获得本地时钟的校正项。
由模型假设本文可以得知,系统中各个节点初始同步到φint内,本文引入一个收敛函数Γ(φint,N,f,ε),该函数用于给出瞬时重同步后所有好时钟的时钟值的最大差值,即系统的时钟精密度。
读取误差ε是一个附加项,将收敛函数分解为式(10)。
Γφint,N,f,ε)=Γφint,N,f)+ε
(10)
在最坏的情况下,一个好的“过期”消息被一个节点接收到,而另一个节点没接收到。因此,单个消息的丢失对于平均值的影响是有限的,可由下式计算。
(11)
由上述计算可以计算出,在考虑读取错误和f个故障(报文丢失、拜占庭故障)的情况下,重同步后全局近似时间偏差的最大值为式(12)。
(12)
在重同步周期λ内,好的时钟的最大偏移率为ρ,因此在同步周期内,将好时钟之间的最大偏移量记为ζ,则下式成立。
ξ=2ρλ
(13)
由于任何两个好的时钟在同一重同步时间间隔内都会偏离,因此对于任何重同步间隔内,下列条件必然成立
Γφint,N,f,ε)≤φint-ξ
(14)
由式(12)和式(14)计算出FTA算法的同步精密度最大值计算式。
(15)
由式(15)可以看出,在前文所建立的模型下,在一个由10个时钟组成的系统中,当只有一个故障的时候,系统会损失14%的同步精密度;当系统中出现两个任意的故障,虽然系统可以容忍,但是这会导致50%的同步精密度损失。经过上述分析可以看出,该算法具有一定的容错能力,并且其容错能力体现在去极值的过程。但是在满足模型假设的情况下,随着拜占庭故障数量不断增多,系统的容错能力大幅度下滑,因此本文将针对这一问题对FTA算法进行改进。
在上述FTA算法的介绍中可以看出其并不能保证完全将系统中存在的故障滤除,因此之后的“求平均”所得到的结果将会受到拜占庭故障的影响。这降低了系统的容错能力,因此本文在FTA算法的基础上采用了“容错中值”的方法,提出了适用于RTEthernet的容错中值算法,即RTEthernet容错中值算法(RTEthernet Fault-Tolerant Midpoint Algorithm, RTE-FTM)算法,这种方法可以避免一个坏的值对中值的扭曲。
RTE-FTM算法沿用了FTA算法中去极值的思想,将每个节点读取到的时钟值集Pi进行去降序排列,再将Pi中最大和最小的f个时钟值剔除,得到一个新的集合Pif,然后将集合Pif中新序列的中值当做目标值,即全局时基。如果序列中的个数为偶数,则用中间两个数的平均值(向下取整)来当作全局时基。
根据上文的模型假设与容错能力的改进,下面以伪代码的形式描述第i轮同步中节点q使用容错中值时钟同步算法进行时钟同步的过程。函数及符号定义如表1所示。

表1 伪代码参数Table 1. Pseud code Parameters
RTEthernet容错中值算法描述如下:
输入:重同步时间。
输出:本地节点即将应用的校正项。

2.GET[q]=TqNOW//每个节点记录当前的时钟值

4.send(message);
5. end if
7.ifTqNOW=Tithen
11.end if
12.end while
综上可以看出,各个节点进行交互各自的本地时钟值,然后将获取到的(包括自己的)时钟值进行降序排列,随后去除f个最大值和f个最小值,并使余下值中的中值作为目标值,再进行代数计算可以得到校正项,最后通过状态修正和速率修正算法来进行时钟的同步。由于RTE-FTM算法是以FTA算法为基础,用中点值代替平均值的计算方法,因此算法的收敛性和有效性证明与FTA算法相类似,这里不重新进行理论的证明。在下一节中将通过实验仿真验证其收敛性和有效性。
5 实验结果与分析
本文在章节4中对FTA算法进行改进,提出了数学模型,本章节中将对RTE-FTM算法的收敛性和容错性进行仿真验证。采用CANoe平台进行仿真实验,CANoe的主要组成部分为:CANdb++、Panel Editor&Panel Designer和编程工具CAPL(CAN Access Programming Language)。
5.1 系统模型的构成
本实验通过7个节点构成一个总线型的拓扑结构,网络中各个节点通过模拟RTEthernet协议进行通信。本文将节点1、节点2、节点4、节点5、节点7设置为无故障节点。根据章节3中的算法模型,将节点3和节点6设置为拜占庭故障节点,其网络拓扑结构如图5所示。

图5 仿真系统拓扑结构Figure 5. The topology structure of the simulation system
5.2 系统参数设置
在上述搭建好的系统模型中,需要确定模型参数值。本节将对仿真实验中具体参数进行确定。根据文献[13,17~18]的研究成果及RTEthernet通信模型的约束条件,确定部分参数为:系统内各节点的最大时钟漂移率ρ=10-4s,各节点初始同步的精密度为φint=20×10-6s,并且在系统中的传输延迟最大为10×10-6s,最小延迟为5×10-6s。即分布式系统内的消息传输延迟在[5,10] μs内,因此系统的传输延迟不确定度为2.5×10-6s,消息延迟范围的中间值δ=7.5×10-6s。根据前文的假设和RTEthernet网络的协议规范可知,仿真系统的重同步周期的下限只存在于ST段和NIT段,上限包含了DYN段,本文考虑普通情况下的重同步周期,即每个循环中包含了ST段和DYN段以及NIT段,故将长度设置为5 ms,循环编号最大编号(gCycleMax)为200。具体参数如表2所示。

表2 系统模型参数Table 2. Parameters of the system model
5.3 仿真结果分析
根据上述系统拓扑结构和参数的设置,本文将对存在故障情况下的FTA和RTE-FTM算法进行收敛性和容错性验证。
控制f=0与系统初始精密度φint=20×10-6s,根据表2的参数来设置每个虚拟节点时钟的环境变量,各个节点分别执行FTA、RTE-FTM两种算法,并将两种算法进行对比分析。从图6可以看出,系统中的各个时钟经过时钟同步算法进行周期性时间校正后,系统的时钟精密度大致稳定在一定的范围内,在无拜占庭故障时钟时,RTE-FTM的精度大于FTA的精度。

图6 无拜占庭故障情况下两种算法的时钟同步精密度对比Figure 6. Comparison of clock synchronization precision between two algorithms without Byzantine fault
控制f=1,2和系统初始精密度φint=20×10-6s,对FTA、RTE-FTM算法进行对比分析及收敛性和容错性验证。从图7可看出,当设置节点3发生拜占庭故障时,经过FTA算法同步后系统的精密度大约为24.47 μs;当有节点3和6都发生拜占庭故障时,整个系统的精密度约为26.32 μs。由此可知,在10个节点的系统中存在两个拜占庭故障时,FTA算法的容错能力降低,同步后系统精密度下降13.7%。对于RTE-FTM算法,当有一个节点发生拜占庭故障时,整个系统的精密度约为27.92 μs,当有两个节点同时发生拜占庭故障时,整个系统的精密度约为28.34 μs。

图7 拜占庭故障情况下两种算法的时钟同步精密度对比Figure 7. Comparison of clock synchronization precision between two algorithms under Byzantine fault
综上,在满足以下两个条件:(1)分布式系统中各个节点初始同步;(2)节点数不超过总数1/3的拜占庭故障节点,可认定RTE-FTM是收敛的。在系统中存在拜占庭故障时,FTA算法的同步精密度损失了13.7%,RTE-FTM算法的同步精密度损失了10.6%。在拜占庭故障数量相同的情况下,RTE-FTM算法比FTA算法的同步精密度损失率降低了3.1%。
6 结束语
工业以太网[19]在工业制造、自动化控制等领域中的应用不断扩大,但是想要能够完成无线到有线的“变革”,不可避免地要考虑实时性和可靠性。因此,工业以太网的时钟同步问题成了关键问题之一。RTEthernet是一种新型的工业级实时以太网协议,其便于实现,且可兼顾传统以太网,但是该协议的时钟同步算法存在容错性低的问题。为此,本文针对FTA算法的容错策略进行修改,即使用“中点值”策略来代替“平均值”策略,提出了RTE-FTM算法来替代原始的基础算法。改进后的算法能够使系统进一步弱化拜占庭故障时钟值对全局时基的影响。在实际系统中存在更为复杂的通信环境,会存在很多没能完全考虑的干扰源,所以在今后的研究中,研究人员将根据实际情况对本文提出的算法进行优化改进。

