基于改进鲸鱼算法的含DG配电网故障区段定位
徐立立,杨 超,曾浩然
(贵州大学 电气工程学院,贵州 贵阳 550025)
电能在工业生产和日常生活中发挥着至关重要的作用。随着国家经济的发展,电力需求量也逐渐增长,电力网络也在不断扩大。根据大量数据显示,90%的停电事故都是由配电网故障所引起的,因此配电网故障率直接影响着供电的可靠性和连续性。快速、准确地定位配电网故障是实现配电网故障隔离、排除和恢复的基础和前提,对减少停电面积、提高配电网运行效率、改善电能质量、缩短停电时间具有重要意义[1-3]。
大量的分布式电源(Distributed Generation,DG)被接入配电网中,导致配电网的拓扑结构和潮流方向发生了改变。对于含分布式电源的配电网,传统故障定位模型已不再适用,因此研究含DG配电网故障定位方法具有重要的现实意义。随着智能电网的快速发展,可通过馈线终端单元(Feeder Terminal Unit,FTU)将故障信息上传到数据采集与监视控制系统(Supervisory Control and Data Acquisition,SCADA),然后馈线自动化系统利用定位算法对配电网进行故障区段定位。基于FTU的配电网故障区段定位方法主要包括两类:一类是基于矩阵运算的矩阵算法[4-5];另一类是人工智能算法,例如遗传算法[6-7]、粒子群算法[8-9]、蝙蝠算法[10-11]、免疫算法[12-13]等。文献[4]利用矩阵算法先确定出疑似故障区域,然后通过电压幅值判据确定出故障区段。该方法虽然能够有效地避免故障误判,但是其在多电源复杂的配电网中定位速度较慢。文献[7]通过调整量子旋转门策略来改进量子遗传算法,并利用Tent映射的混沌优化思想使算法跳出局部最优解,改进后的算法在定位故障区段方面应用效果良好。文献[8]借鉴了免疫系统的信息处理机制,并采用了抗体浓度调节机制与免疫选择操作来优化粒子群算法。优化后的算法在保证种群多样性的同时,也提高了算法的收敛性能,有效提高了故障定位的准确性。文献[12]提出了一种将量子计算与免疫算法相结合的配电网故障定位方法,可以减少种群规模,加快算法收敛速度,为复杂度高和容错性差的故障定位问题提供了一种求解方法。虽然目前已提出的优化算法有很多种,但是这些算法仍然存在局部收敛、定位速度较慢等缺点。现在的研究主要通过改进算法或者混合算法来提高智能算法的性能,使定位结果更加准确,缩短了定位时间。
鉴于上述分析,本文提出了一种基于改进鲸鱼算法(Improved Whale Optimization Algorithm,IWOA)的含分布式电源配电网故障定位方法。在传统鲸鱼算法的基础上,采用自适应惯性权重策略对鲸鱼算法加以改进,有效地平衡鲸鱼算法的全局和局部搜索能力。本文进行了仿真测试,进一步验证了该算法的可行性与收敛性。
1 含DG配电网故障定位模型
当配电网发生故障后,首先利用FTU采集故障过流信息并进行编码;然后通过IWOA算法优化使适应度函数达到最小化;最后定位出故障区段。在整个故障定位模型中,故障电流的编码方式、开关函数以及适应度函数的正确建立是实现配电网故障定位的关键。
1.1 故障电流编码
对于传统的单辐射状配电网故障过流信息Ij,采用0-1二进制编码的方法,其取值只能是0或1。当开关流过故障电流,用数字1编码表示,否则用数字0编码表示。由于分布式电源接入配电网将造成配电网拓扑结构和故障电流的方向发生变化[14],故需要重新定义故障电流的编码方式。假定电流由主电源流向末端负载的方向为正方向,则当开关流过的故障电流与正方向相同时,用数字1编码表示;当开关没有故障电流流过时,用数字0编码表示;当开关流过的故障电流与正方向相反时,用数字-1编码表示。新定义的编码方式如式(1)所示。
(1)
如图1所示是一个含DG配电网简化模型。图中S表示系统主电源,Si、Li分别表示分段开关和馈线区段,DG1和DG2表示两个分布式电源。假设区段L4、L7发生故障,则此时开关S1、S2、S3、S4、S6、S7流过正向故障电流,用数字“1”编码表示;开关S5、S8、S9流过反向故障电流,用数字“-1”编码表示;开关S10、S11没有流过故障电流,用数字“0”编码表示。所以FTU上传的信息可表示为[1 1 1 1 -1 1 1 -1 -1 0 0]。
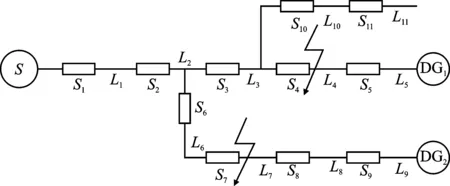
图1 含DG配电网简化模型Figure 1. Simplified model of distribution network with DG
1.2 开关函数
开关函数反映了馈线区段信息与故障电流信息之间的相互关系,所构建的模型将会直接影响到故障定位的准确度。文献[15]构造了一种适用于单辐射状配电网故障定位的开关函数,其表达式如下
(2)
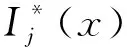
式(2)只适用于单电源配电网故障定位,不适用于含有一个主电源和多个分布式电源的配电网,其在定位时会出现误判,从而影响故障定位的准确性。因此,针对多电源配电网的单重、多重故障定位问题,需要建立一种新的开关函数。文献[16]所构造的开关函数可以动态地反映各个分布式电源的接入情况,其表达式为
(3)
(4)
(5)
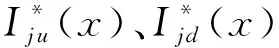
1.3 适应度函数
适应度函数的准确性是决定故障定位模型能否正确定位出故障区段的关键。由于FTU工作环境恶劣且易受到通信干扰,可能会出现上传信息发生畸变或者缺失的情况。为了防止在故障定位过程中发生误判情况,本文增加了一项误判项来提高适应度函数的容错性,其表达式如下
(6)
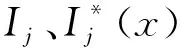
2 改进鲸鱼算法基本原理
2.1 传统鲸鱼算法
鲸鱼算法(Whale Optimization Algorithm,WOA)[17]是一种新型智能优化算法,其通过模拟座头鲸独特的搜索方式和围捕机制来寻找最优解。该算法主要包含3个重要阶段:包围猎物阶段、捕食猎物阶段和搜索猎物阶段。
2.1.1 包围猎物阶段
由于猎物在搜索空间内的位置不是已知的,因此假设当前种群的最优位置为目标猎物,其他鲸鱼根据该位置向目标猎物移动,这个阶段的位置更新计算式如下
D=|C×X*(t)-X(t)|
(7)
X(t+1)=X*(t)-A×D
(8)
式中,t表示当前迭代次数;X*(t)表示当前种群最优解的位置;X(t)当前个体的位置;||代表绝对值运算;D表示包围步长;A和C是两个参数,计算式为
A=2a×r1-a
(9)
C=2×r2
(10)
a=2-2t/tmax
(11)
式中,r1和r2为[0,1]之间的随机数;a为收敛因子,变化范围为[2,0];tmax表示最大的迭代次数。
2.1.2 捕食猎物阶段
鲸鱼在捕食猎物阶段主要利用泡泡网攻击策略向猎物移动,该策略包括两种机制:一种是收缩包围机制,利用式(8)来更新鲸群个体位置。参数A是一个取值在[-a,a]范围内的随机数,其波动范围随收敛因子a减少而减少。随着t的增加,参数A和收敛因子a减小,包围圈减小,计算精度提高;另一种是螺旋更新位置机制,其模仿了鲸鱼螺旋游走捕食猎物的方式,其计算式为
D′=|X*(t)-X(t)|
(12)
X(t+1)=D′×ebl×cos(2πl)+X*(t)
(13)
式中,D′表示鲸鱼个体到当前最优解的距离;b为定义螺旋形状的常数;l为[0,1]间的随机数。
由于鲸鱼在捕食过程中会同时进行收缩包围和螺旋前进,所以假设鲸鱼群体选择相同的概率,即0.5,来进行位置更新
(14)
式中,p为[0,1]间的随机数。
2.1.3 搜索猎物阶段
当参数A的绝对值大于等于1时,鲸鱼不再通过选择猎物来更新位置,而是随机搜索猎物。利用这种位置更新策略可以有效避免算法陷入局部最优
D=|C×Xrand(t)-X(t)|
(15)
X(t+1)=Xrand(t)-A×D
(16)
式中,Xrand(t)表示第t次迭代随机选择的个体位置。
2.2 鲸鱼算法的改进
鲸鱼算法具有原理简单、参数少和寻优能力强等优点,已被成功运用于实际工程领域中,例如优化调度[18]、特征选择[19]和图像分割[20]等。但是在寻优过程中,该算法存在一些缺点,其收敛速度较慢,寻优精度较低,还容易陷入局部最优等。本文引入自适应惯性权重策略来优化WOA算法,其中自适应权重的参数ω为
(17)
式中,ωmax、ωmin分别表示权重系数的上、下限,通常ω的取值范围为[0.4, 2]。本文的ωmax、ωmin分别取0.9和0.4。权重参数ω随着迭代次数t的增加逐渐由0.9减小至0.4。权重参数ω在迭代前期取得较大值,使鲸鱼算法具有较强的全局搜索能力,防止其陷入局部极值;在迭代后期取得较小值,此时鲸鱼算法有较强的局部搜索能力,可加速算法收敛得到最优解。将式(17)带入式(14)可得到如下计算式。
(18)
X(t+1)=D′×ebl×cos(2πl)+ωX*(t),p≥0.5
(19)
2.3 IWOA算法定位流程图
根据章节1中建立的含DG配电网的定位模型,依据FTU上传的故障电流信息,利用IWOA算法对定位模型进行求解,并最终定位出故障区段。IWOA算法的定位流程图如图2所示。
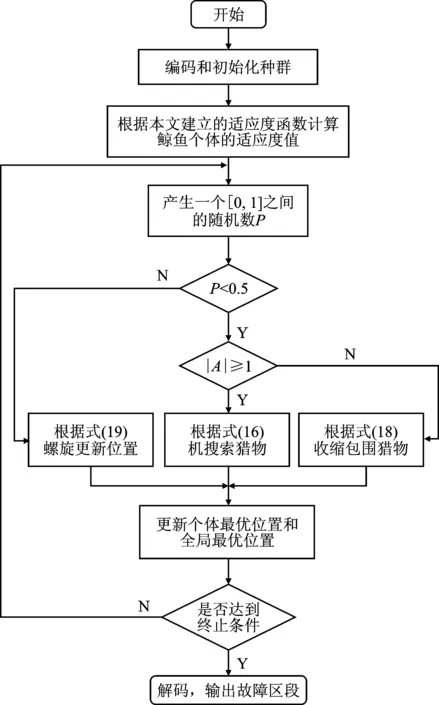
图2 IWOA算法定位流程图Figure 2.Flow chart of IWOA algorithm positioning
3 算例分析
本文以图3所示的33节点配电网模型为例进行仿真测试。在图3中,分别用S和DG1、DG2、DG3来表示1个主电源和3个分布式电源; 用K1、K2、K3表示3个分布式电源的接入开关,其取值为1或者0,其中1表示分布式电源接入系统,0表示分布式电源没有接入系统;编号1~33为开关节点;(1)~(33)为馈线区段。
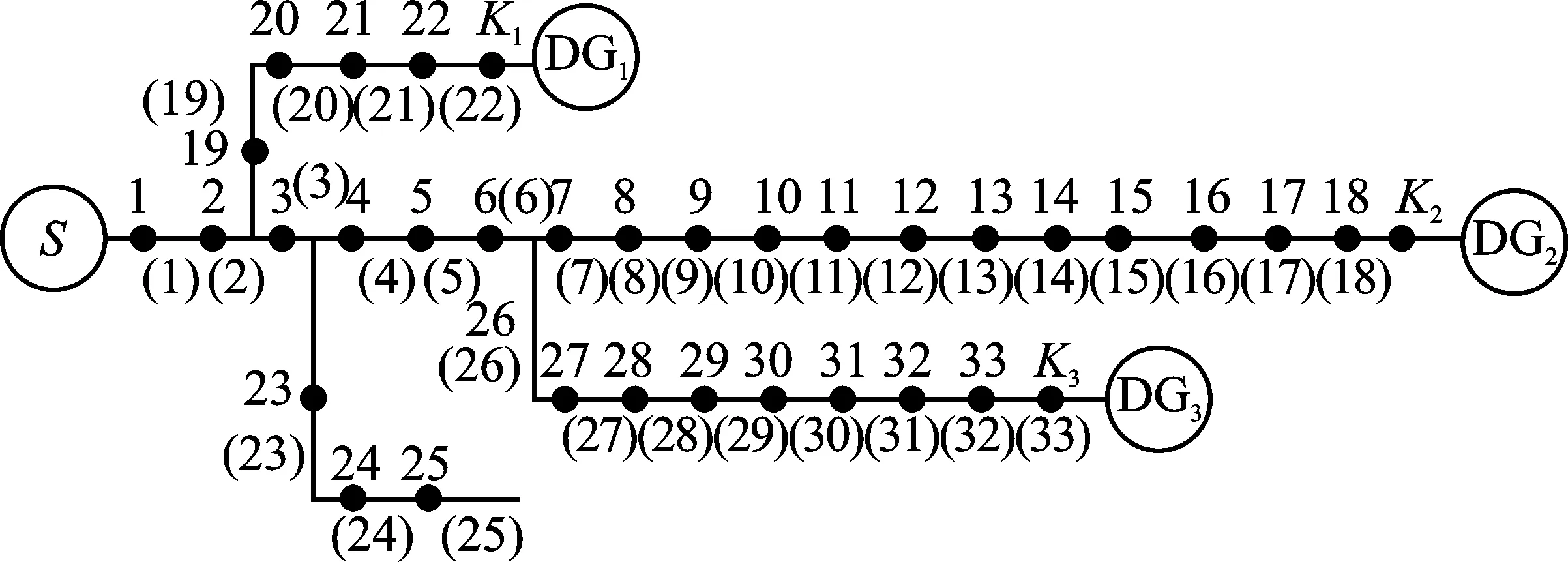
图3 33节点配电网Figure 3. 33-nodes distribution network
本文利用MATLAB软件2016a 版本进行仿真测试。根据本文所提出的IWOA算法原理编写MATLAB程序并设置相关程序参数,其中鲸鱼种群规模为50,最大迭代次数为50,种群空间维度为33,其他参数设置见章节2.1。
3.1 单重故障分析
为了验证本文所提算法的可行性和准确性,根据编写的程序和相应的参数设置,针对图3所示的配电网进行单重故障定位仿真测试。仿真过程中需考虑分布式电源接入系统的数量差异以及上传信息畸变等情况。由于故障位置是随机变化的,所以选择5种具有代表性的配电网故障情况进行仿真测试,定位结果如表1所示。
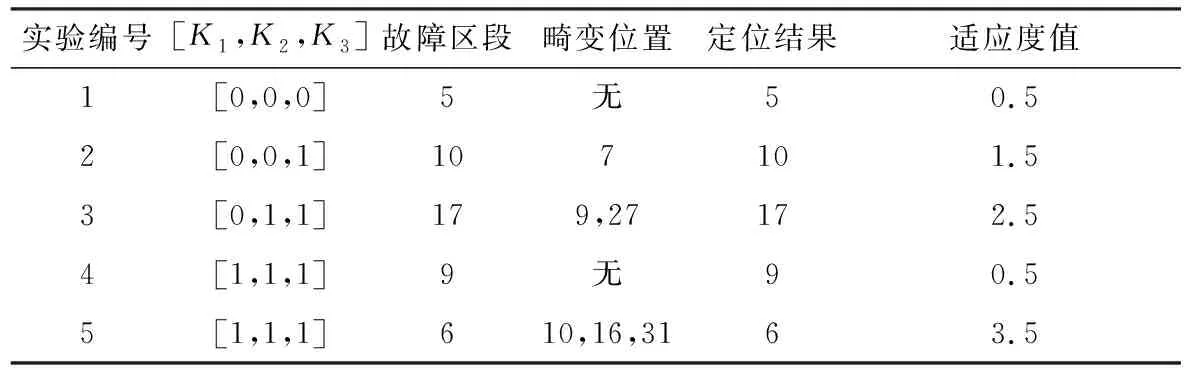
表1 单重故障定位结果Table 1. Single fault location results
从表1可知,当没有分布式电源接入配电网时,K1、K2、K3的取值都为0,定位结果与预设的故障区段一致,因此本文所构建的定位模型同样适用于单辐射状配电网的故障区段定位。在无需考虑分布式电源接入数量以及信息畸变的情况下,IWOA算法能够准确地定位出故障区段。表1中实验 3假设区段(17)发生故障,此时配电网接入了DG2和DG3两个分布式电源,且开关9和开关27的信息分别由1和-1畸变为0,故 FTU上传的信息编码为[1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 -1 0 0 0 0 0 0 0 -1 0 -1 -1 -1 -1 -1 -1]。经过IWOA算法定位后的输出结果为[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0],最优适应度值为2.5。由此可知,在含分布式电源的配电网发生单重故障的情况下,改进鲸鱼算法能够快速、准确地找到故障区段,并且在开关信息发生畸变时,改进鲸鱼算法仍然可以准确地定位出故障区段,证明该算法具有良好的容错性。
3.2 多重故障定位
假设图3所示的配电网发生多重故障,同时考虑分布式电源的接入和信息畸变情况,测试结果如表2所示。
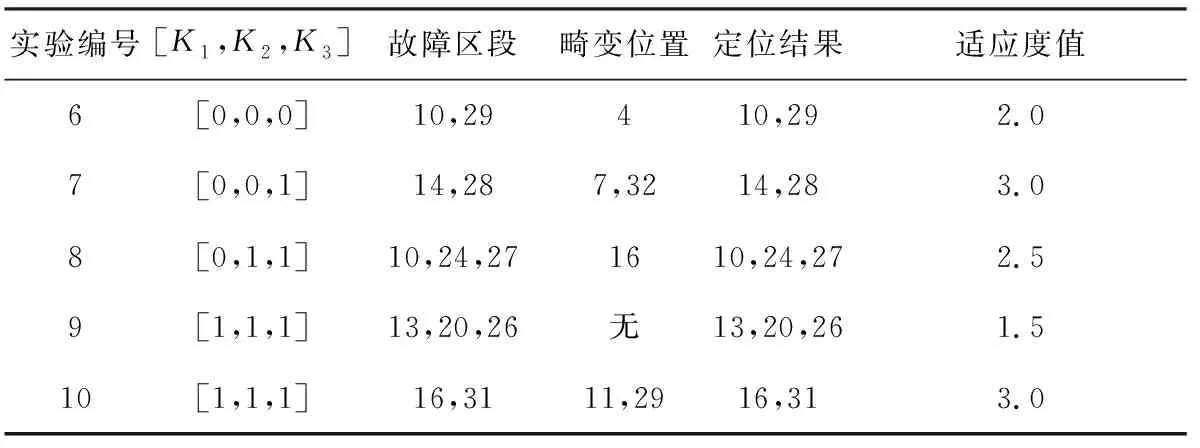
表2 多重故障定位结果Table 2. Multiple faults location results
从表2可知,实验10中馈线区段(16)和(31)发生故障,配电网接入3个分布式电源,开关11和29的信息发生畸变,均由1畸变为0,此时FTU上传的故障信息编码为[1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 -1 -1 -1 -1 -1 -1 0 0 0 1 1 1 0 1 1 -1 -1],输出结果为[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0],最优适应度值为3。仿真结果表明,本文所提出的算法同样适用于配电网多重故障定位,而且在开关信息发生畸变时能够准确定位出故障区段位置。
3.3 不同算法性能对比
为了验证本文所提算法的性能优势,对改进鲸鱼算法和鲸鱼算法进行故障定位对比分析。针对配电网发生单重故障无信息畸变、单重故障有信息畸变、多重故障无信息畸变和多重故障有信息畸变这4种故障情形进行仿真测试。假设4种情形依次为第1种~第4种,且系统接入3个分布式电源,IWOA与WOA两种算法运行的适应度变化情况如图4~图7所示。
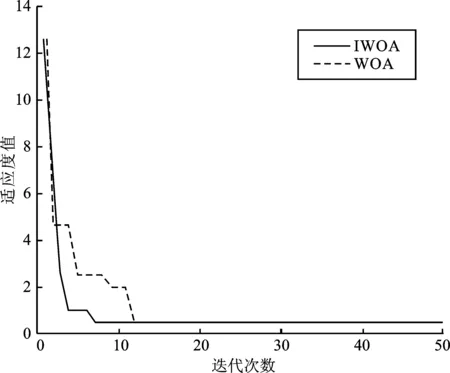
图4 第1种故障情形适应度变化曲线Figure 4. Fitness curve of the first fault condition
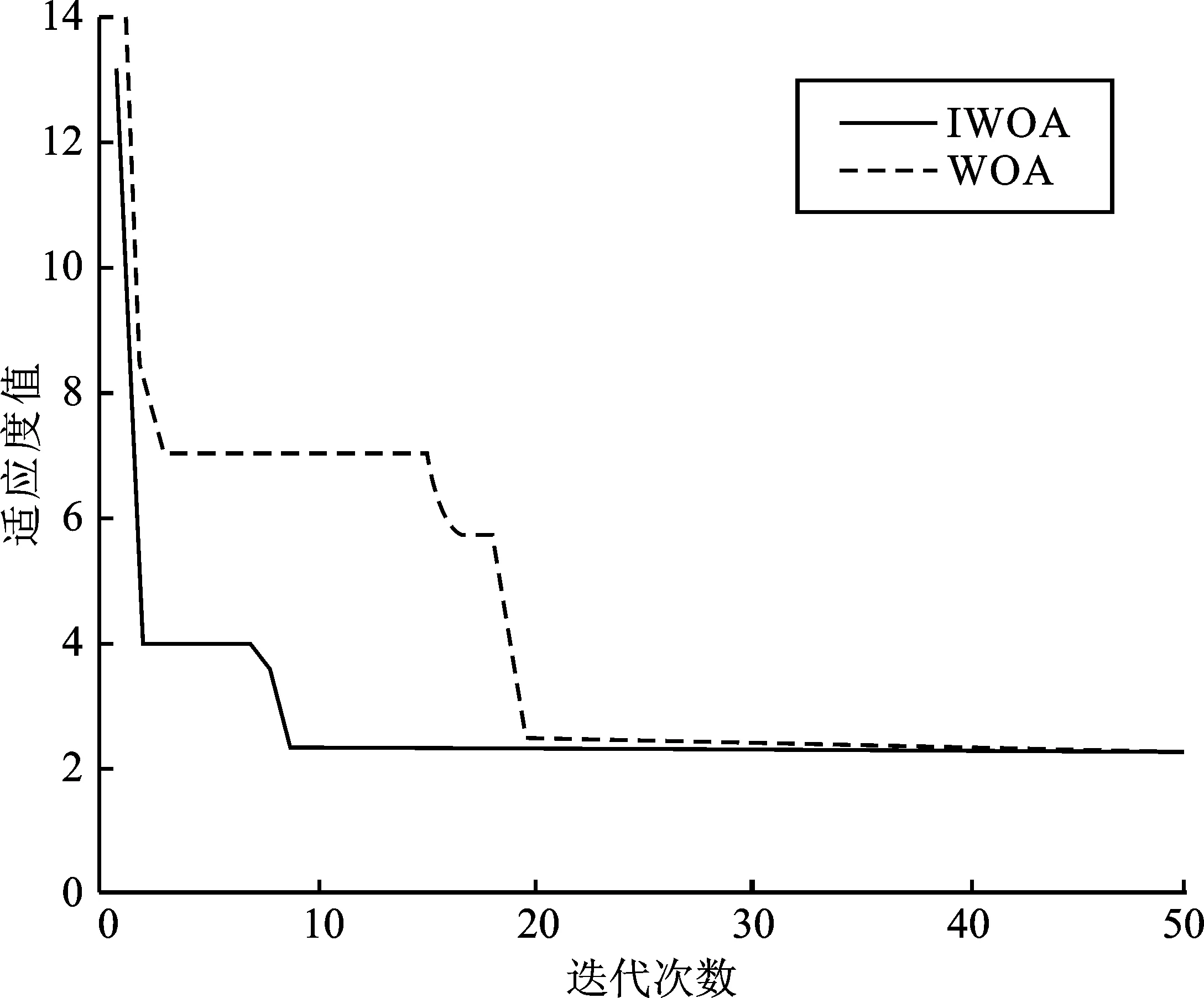
图5 第2种故障情形适应度变化曲线Figure 5. Fitness curve of the second fault condition
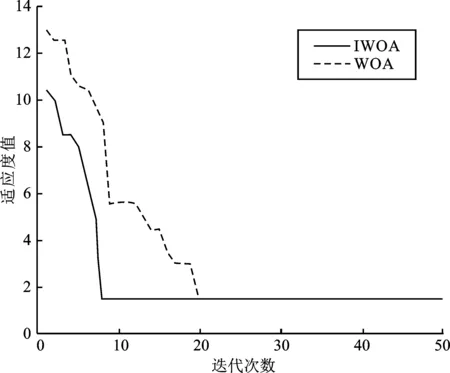
图6 第3种故障情形适应度变化曲线Figure 6. Fitness curve of the third fault condition
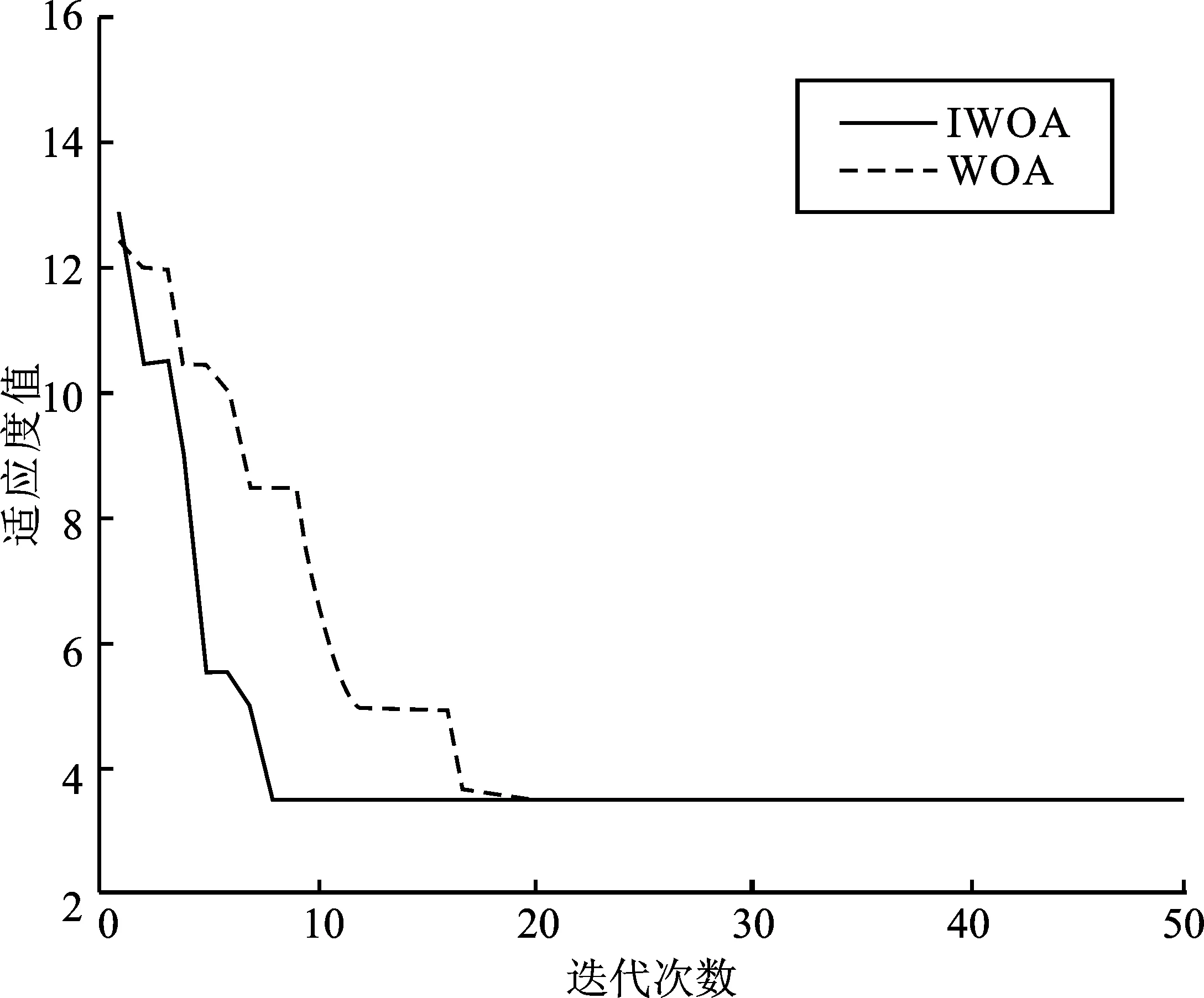
图7 第4种故障情形适应度变化曲线Figure 7. Fitness curve of the fourth fault condition
图4中,预设故障馈线(12)发生故障,无信息畸变。图5中,预设馈线区段(12)发生故障,开关7、16信息发生畸变。图6中,预设馈线区段(13)、(20)、(26)发生故障,无信息畸变。图7中 预设馈线区段(13)、(20)、(26)发生故障,开关6、31信息发生畸变。由图4~图7可知,在配电网发生上述4种故障情形下,WOA和IWOA算法都能达到最优适应值,并准确定位出故障区段。但是在4种故障情形下,IWOA算法获得最优解的迭代次数较少,均小于10代,而WOA算法迭代次数在20次左右。当信息发生畸变时,IWOA算法仍能快速地定位出故障区段。以上结果证明相较于传统鲸鱼算法,改进后鲸鱼算法的收敛速度有较大优势,容错性也较高。
假设配电网发生上述4种故障情形,分别用两种算法进行50次仿真测试,对两种算法的平均迭代次数和定位准确次数进行统计,对比结果如表3所示。
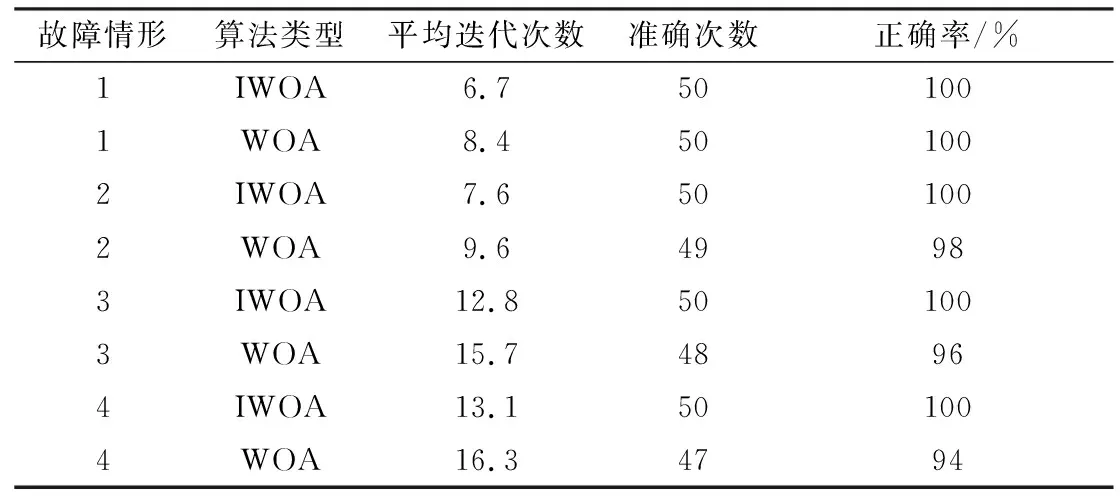
表3 两种算法定位结果对比Table 3. Comparison of positioning results of two algorithms
由表3可知,在上述4种故障情形下,IWOA算法比WOA算法的定位准确性更高,而且平均迭代次数更少。由此可知改进后的鲸鱼算法具有更高的定位准确率和收敛速度。
4 结束语
本文提出一种改进鲸鱼算法,用于解决含分布式电源的配电网故障区段定位问题。本文将自适应惯性权重策略引入到鲸鱼算法,不仅增强了个体的局部搜索能力,还兼顾了算法的全局搜索能力。改进后的鲸鱼算法不仅具有较快的收敛速度,还具有较强的稳定性和更好的优化效果。本文构建的配电网定位模型适用于含DG配电网的单重、多重故障定位。此外,当开关信息发生畸变时,该定位模型具有较强的容错能力。本文所提的IWOA算法在考虑分布式电源投切的数量和信息畸变的情况下能准确定位出配电网的单重故障和多重故障。相较于传统鲸鱼算法,IWOA算法的定位速度更快,容错性更好,定位的可靠性得到了显著提升。

