基于压缩感知理论的高能闪光照相密度反演方法

芦存博,盛云霄

(1.北京计算机技术及应用研究所，北京 100854; 2.陆军装甲兵学院 演训中心，北京 100072)

高能闪光照相是在核禁试的情况下，进行核武器研究的主要手段之一。高能闪光照相能够验证以前在核试验情况下形成的核武器编码，并能对不完善的编码进行修正，以之来推动在核禁试情况下的核武器研究。

高能闪光照相成像系统的结构由X射线源、准直器、客体、图像接收系统组成。准直器主有两个作用：(1)降低被照客体的动态范围，便于图像接收系统接收图像；(2)降低成像平面上散射X射线强度，以便提高客体中心区域的对比度。闪光照相的图像接收系统除了氯化银的胶片外，还有CCD相机、磷探测器等。在闪光照相中，由光源发出的X射线穿透照相客体后到达图像接收系统，可记录X射线的空间强度分布，形成闪光照相图像。

高能闪光照相利用X射线的穿透能力以及它与物质相互作用的性质，根据成像平面上单位面积的X射线能量空间分布，通过图像分析来提取客体的结构信息和密度信息，进而确定客体的几何性质和物理性质，从而对客体及其内部结构进行定量和物理诊断。

利用高能闪光照相获得客体的几何界面位置以及空间密度分布对研究客体在爆轰过程中的行为具有重要意义。在核物理领域，为了研究爆炸物体在某一时刻的物理状态，例如爆轰过程中物质密度的变化，常使用高能X射线照射物体，并根据投影信息重建密度分布等内部结构信息。高能X射线照相诊断的客体信息 “隐藏”于高能X射线照相得到的投影图像中。高能闪光照相属于投影成像技术，密度图像重建技术是高能闪光照相图像处理技术中的重要研究内容[1]。

高能闪光照相图像重建问题是一个典型的高维线性反演问题。现有的图像重建算法大致有3种[2]：(1)解析算法，例如Abel变换、Radon变换、滤波反投影(Filter Back Projection，FBP)等；(2)迭代算法，例如代数重建技术(Algebraic Reconstruction Technique，ART)、约束共轭梯度(Constrained Conjugate Gradient，CCG)法、偏微分方程(Partial Differential Equation，PDE)约束法等；(3)统计算法，例如极大似然模型和期望最大化(Maximum Likelihood-Expectation Maximum，ML-EM)方法、马尔可夫链蒙特卡罗(Markov Chain Monte Carlo，MCMC)方法。

在高能闪光照相中，每次实验只有一个或两个方向的投影数据，因此要求密度反演的客体必须具有轴对称性。这是因为，如果客体是轴对称的，那么在与对称轴垂直的平面上从不同方向得到的射线投影图像是等效的，从而只需1幅投影图像即可进行密度重建工作。如果客体不具有轴对称性，就需要多次实验。因此，需要研究少数投影数据条件下的密度反演问题。但是国内在非轴对称客体的密度反演技术方面的研究较少。

压缩感知(Compressive Sensing，CS)[3-9]由于考虑了信号的稀疏性或可压缩性而成为一种有效的信源处理技术，其核心是利用测量矩阵实现了对原始信号从高维空间到低维空间的线性映射，然后在重建算法中利用信号的稀疏性/可压缩性实现了原始信号的高概率精确重建。在高能闪光照相下，待重建客体的物质密度图像可以看做是一种简单的三维图像。通常情况下，组成客体的物质数量不会太多，并且物质的分布有一定规律，因此在表征客体的三维密度图像中，不同区域之间相同密度元素值的相似性可以在图像重建算法设计中作为先验信息加以利用，其可以用CS的思想表征。

针对高能闪光照相密度重建算法，国内在轴对称客体方面开展了大量数值模拟工作[1-2， 10-12]。但是目前还没有关于非轴对称客体方面的工作，对于基于CS理论的重建算法的研究也较少。利用先验信息约束重建图像并结合CS理论而形成的重建算法将开辟一条闪光照相密度反演的新路径。利用这种算法获得高质量的重建图像，对提高核武器初级诊断闪光实验的客体界面和密度测量的精度具有重要的现实意义。

现有的利用CS思想的全变差(Total Variation，TV)类算法[13-14]虽然考虑了图像的局部相似性，但没有考虑图像的非局部相似性，图像的先验稀疏信息利用还不充分，图像的重建精度还有进一步提升的空间。为了解决这一问题，本文将组稀疏模型集成于TV框架之下，提出了一种基于组稀疏正则化(Group-Sparsity Regularization，GSR)的全变分重建技术(TV-GSR)，充分利用图像的先验稀疏信息，利用客体的上、下、左、右4点对称性降低图像重建的规模，增加了重构精度，加快了重建速度。仿真实验表明，文中提出的TV-GSR算法同时考虑了客体图像的局部相似性和非局部自相似性，充分利用了图像的先验稀疏信息，提升了图像在无噪声和有噪声情况下的重建精度，对于高能闪光图像和纹理细节丰富的CT(Computed Tomography)图像都有良好的效果，具有普适性。

1 闪光照相图像重建的数学模型

在高能闪光照相中，虽然客体处于爆轰压缩的高速运动状态，但是由于X光持续时间特别短，在此时间内客体的压缩运动位移及密度变化非常小，因此可以认为在X光持续时间内的客体处于静止状态[15]。考虑单能、无模糊、无散射的理想简化情况，闪光照相的投影图像可以认为是沿一组平行光束进行采集的。闪光照相成像过程可以简述为：由光源发出的X光穿透照相客体后到达图像探测平面，由图像接收器件记录X光的空间强度分布，形成照相图像。闪光照相成像过程可以表示为

(1)

式中，I(x，y)为X光的透射强度；I0为X光的入射强度；μ(x，y，z)为照相客体质量吸收系数的空间分布；ρ(x，y，z)为照相客体的空间密度分布；z为X光的传播方向。令p(x，y)=ln[I0/I(x，y)]表示X光穿透客体的光程，则式(1)可以变换为

(2)

式(2)即为闪光照相投影成像模型，其矩阵形式为

p=Aμ1

(3)

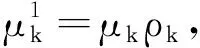
2 组稀疏模型

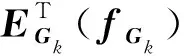
(4)

式中，操作符/表示两个矩阵元素之间的除法；1Ps×m为与fGk相同大小的全1矩阵。

令DGk为每一个结构组fGk的自适应字典。在此模型中，定义e为f的估计，在每次迭代中都可以得到e。令eGk为结构组fGk的相应估计。一旦得到eGk，对其应用奇异值分解(Singular Value Decomposition，SVD)，可得

(5)

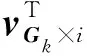
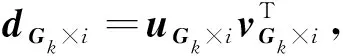
(6)

式中，DG表示所有DGk的级联；αG表示所有αGk的级联。

3 TV-GSR算法的具体描述

TV-GSR算法包括两个模块，分别为TV算法模块和GSR算法模块，这两个模块是相互独立的，级联到一起的。将GSR模型集成于TV框架之下，对每次迭代TV的重建结果使用提出的GSR模型进行正则化处理，最后把GSR正则化的结果作为下一次TV迭代的初始图像，这样循环往复直到满足停止准则为止。本文中TV算法使用文献[18]中的算法，下面重点介绍GSR算法模块。

GSR的优化问题可以表示为

(7)

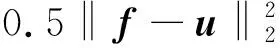
(8)

但是，式(8)很难求解，因为l0范数优化问题是非凸的。本文用分裂Bregman迭代(Split Bregman Iteration， SBI)算法[17]求解这个问题。考虑如下约束优化问题

(9)

根据SBI算法，式(9)中的最小化问题可以被分裂成下列3个子问题。

(10)

(11)

bt+1=bt-(xt+1-Gyt+1)

(12)

对于SBI算法，将相关的初始值设置为t=0，选择μ>0，b0=0，x0=0，y0=0。式(10)～式(12)循环往复直到满足停止准则为止。

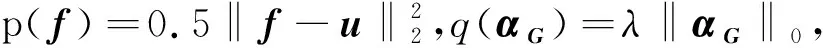
(13)

(14)

(15)

然后，式(8)所示的最小化问题被转换成关于f和αG的两个子问题。对于给定的αG，式(13)所示的关于f的子问题是一个严格的二次凸优化问题，其可以被定义为

(16)

通过设置P1(ft+1)的梯度为0，可以获得式(16)的闭环求解，其为

(17)

式中，E是单位矩阵。对于给定的f，式(14)所示的关于αG的子问题可以被定义为

(18)

式中，et+1=ft+1-bt。根据文献[19]，式(18)可以被转化为

为减少道岔故障对有轨电车运营带来的影响，一般宜在 3 个方向设置单渡线供道岔发生故障后临时折返。双Y道岔在各种故障情况下临时运行情况如图 4 所示。

(19)

式中，ξ=(λ×Ps×m×n)/(μ×N)。然后，式(18)转化为关于所有结构组fGk的n个子问题。由于fGk=DGkαGk，eGk=DGkβeGk，每一个结构组fGk的最小化问题可以被定义如下

(20)

因此，式(20)的一个闭环求解为

(21)

式中，hard(·)为硬阈值函数。一旦对于所有结构组的αGk被计算出来，关于αG的子问题的最终求解也能被确定。

鉴于目前武器诊断的应用实际，客体被假设满足上、下、左、右4点对称(参照方向为初始的射线方向)。重建三维客体只需要重建出上半部分的客体即可，下半部分的客体可以利用上下对称性得到。

TV-GSR算法的具体实现可描述为：利用TV对每次迭代得到的数据进行正向投影到图像域，再对TV重建的相应二维图像切片的左半部分图像和右半部分图像进行加权平均，使用提出的GSR模型对加权平均后的图像进行正则化处理，最后利用左右对称性把GSR正则化的结果恢复出原始大小的图像，并将此图像作为下一次TV迭代的初始图像，这样循环往复直到满足停止准则为止。

4 实验仿真及分析

本章节通过简单三维客体和复杂CT图像上的数值仿真，对比了TV-GSR算法、TV[18]算法、SART算法和SART-GSR[17]算法的密度重建精度。投影方式采用多角度的投影，在0°～180°之间均匀取值，例如当投影图像为3幅时，投影角度为0°、60°、120°。在无噪声重建中，对比算法为TV算法、SART算法和SART-GSR算法；在有噪声重建中，投影数据被高斯噪声污染，对比算法为TV算法。

4.1 简单三维客体实验

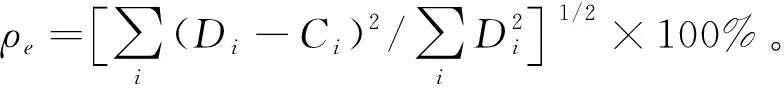
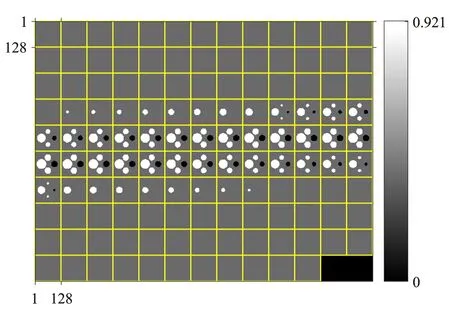
图1 原始三维客体密度图像的二维展开图Figure 1. Two-dimensional expanded structure of original three-dimensional object

实验1在无噪声的情况下，当投影角度的数量变化时，不同重建算法的重建均方根误差对比曲线如图2所示。

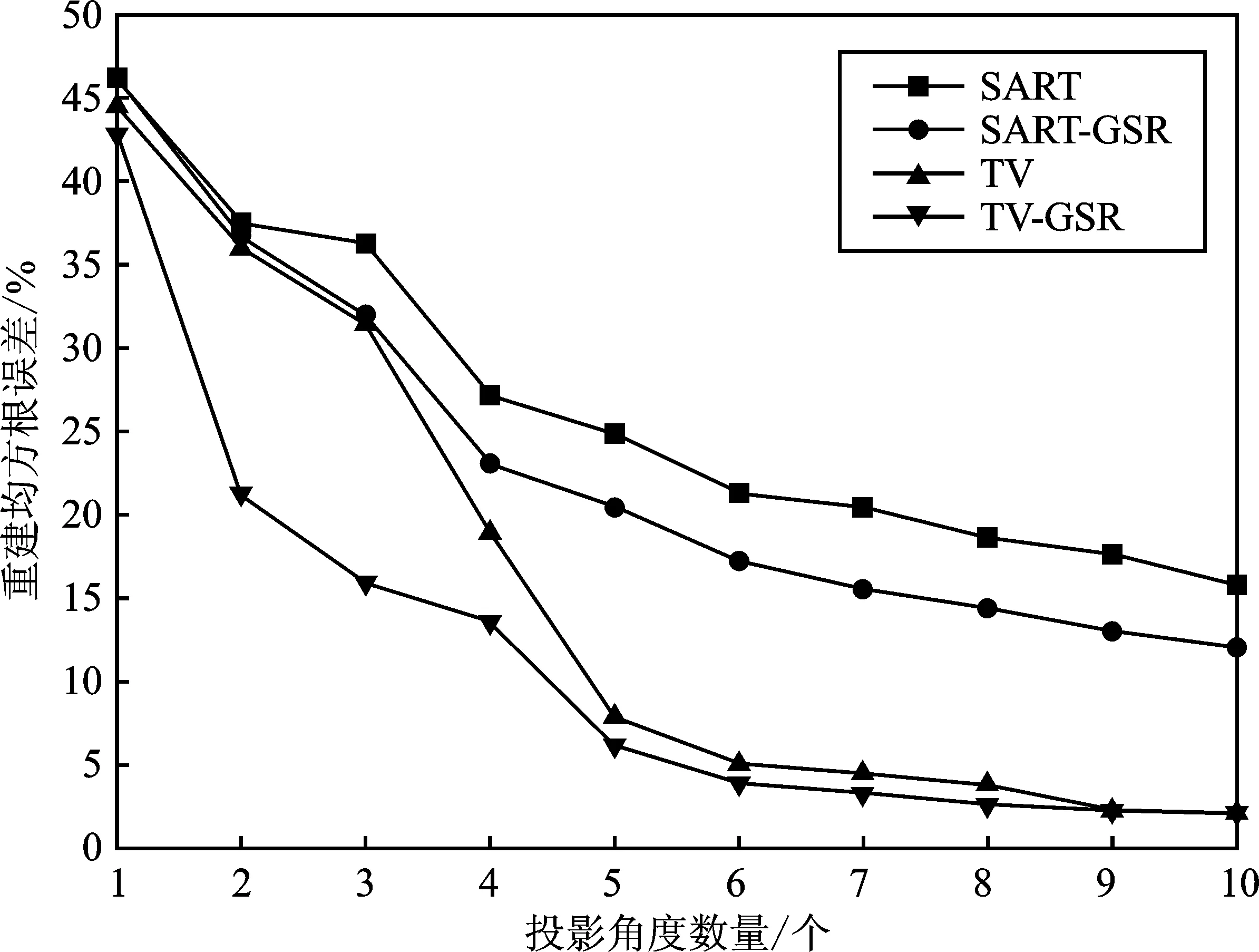
图2 不同投影角度数量下的重建均方根误差Figure 2. Reconstruction root-mean-square error under different number of projection angle

如果客体整体的重建密度误差在5%以下就满足重建精度要求，7个方向和6个方向的投影图像对于TV算法和TV-GSR算法分别来说基本是最佳的投影图像数目。GSR的加入在保证成像质量的情况下，有效改善了TV算法的性能，可以减少一个方向的投影图像，从而降低辐射剂量。

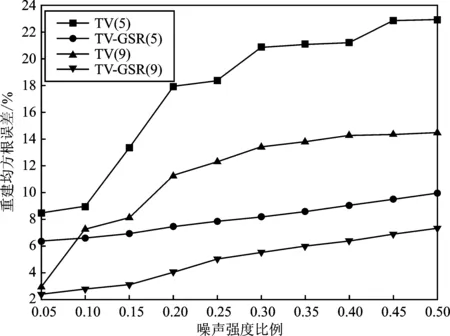
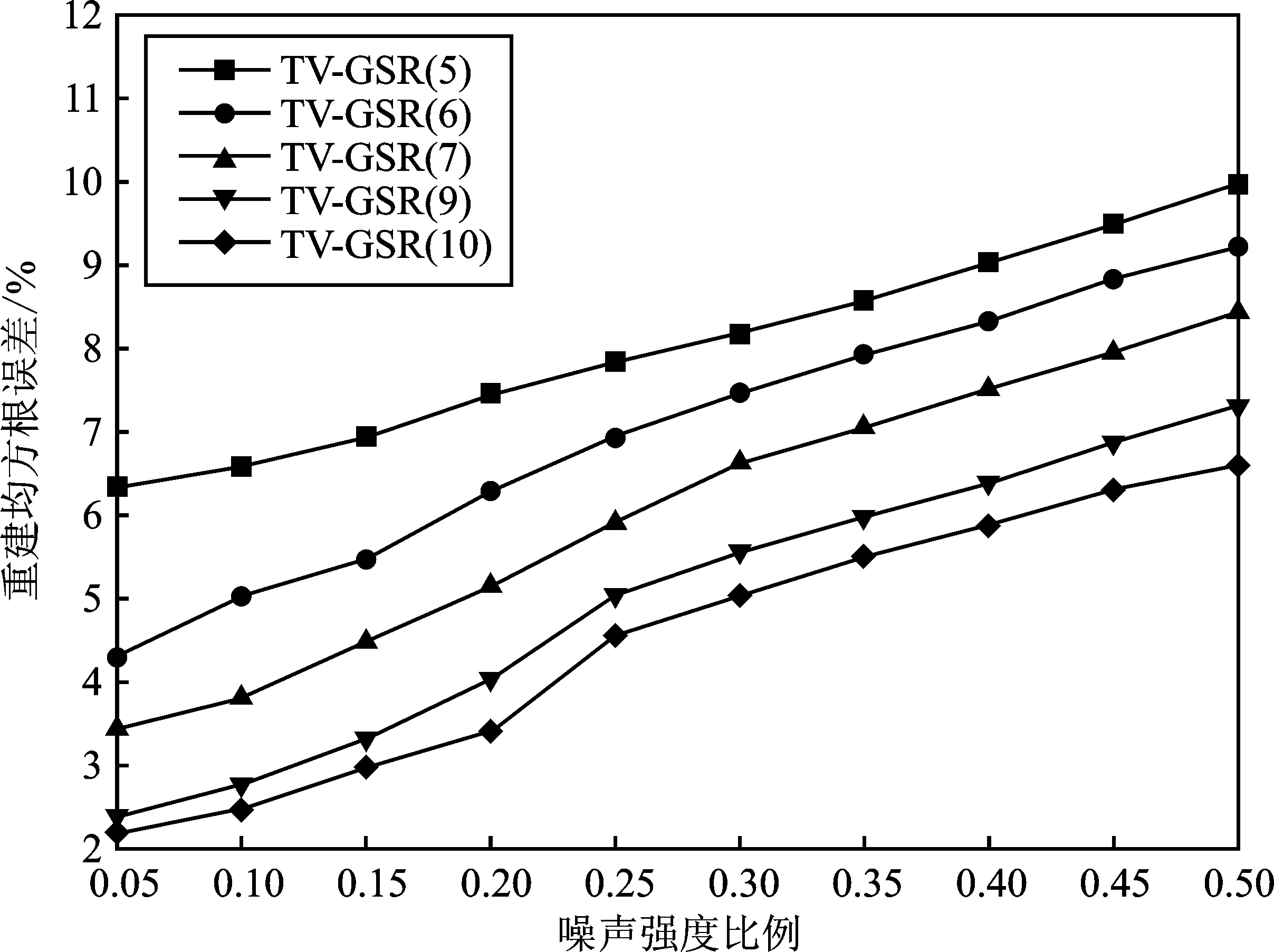
实验2在有噪声的情况下，当投影角度的数量为5和9时，不同噪声强度比例下的TV和TV-GSR重建算法的重建均方根误差对比曲线如图3(a)所示；当投影角度的数量变化时，不同噪声强度比例下的TV-GSR重建算法的重建均方根误差对比曲线如图3(b)所示。仿真图中算法标注括号里面的数字表示投影角度的数量。

(a)

(b)图3 不同噪声强度比例下的重建均方根误差(a)投影角度的数量为5和9的情况 (b)不同投影角度数量的情况Figure 3. Reconstruction root-mean-square error under different percentage of noise strength(a)The case that the number of projection angle equals 5 and 9 (b)The case that the number of projection angle differs

从图3可以看出，与TV算法相比，TV-GSR算法改善了客体的抗噪声性能，甚至在高斯噪声强度比例高达50%的情况下，客体整体的重建密度误差仍然在10%以下。而对于TV算法来说，在投影角度的数量为5时，当高斯噪声强度比例为15%时，客体整体的重建密度误差超过10%；而对于投影角度的数量为9时，当高斯噪声强度比例为20%时，客体整体的重建密度误差超过10%。

4.2 复杂CT图像实验

待重建客体为大小为128×128的CT二维图像切片“pelvic_image_up”，其满足左右对称性，如图4所示。

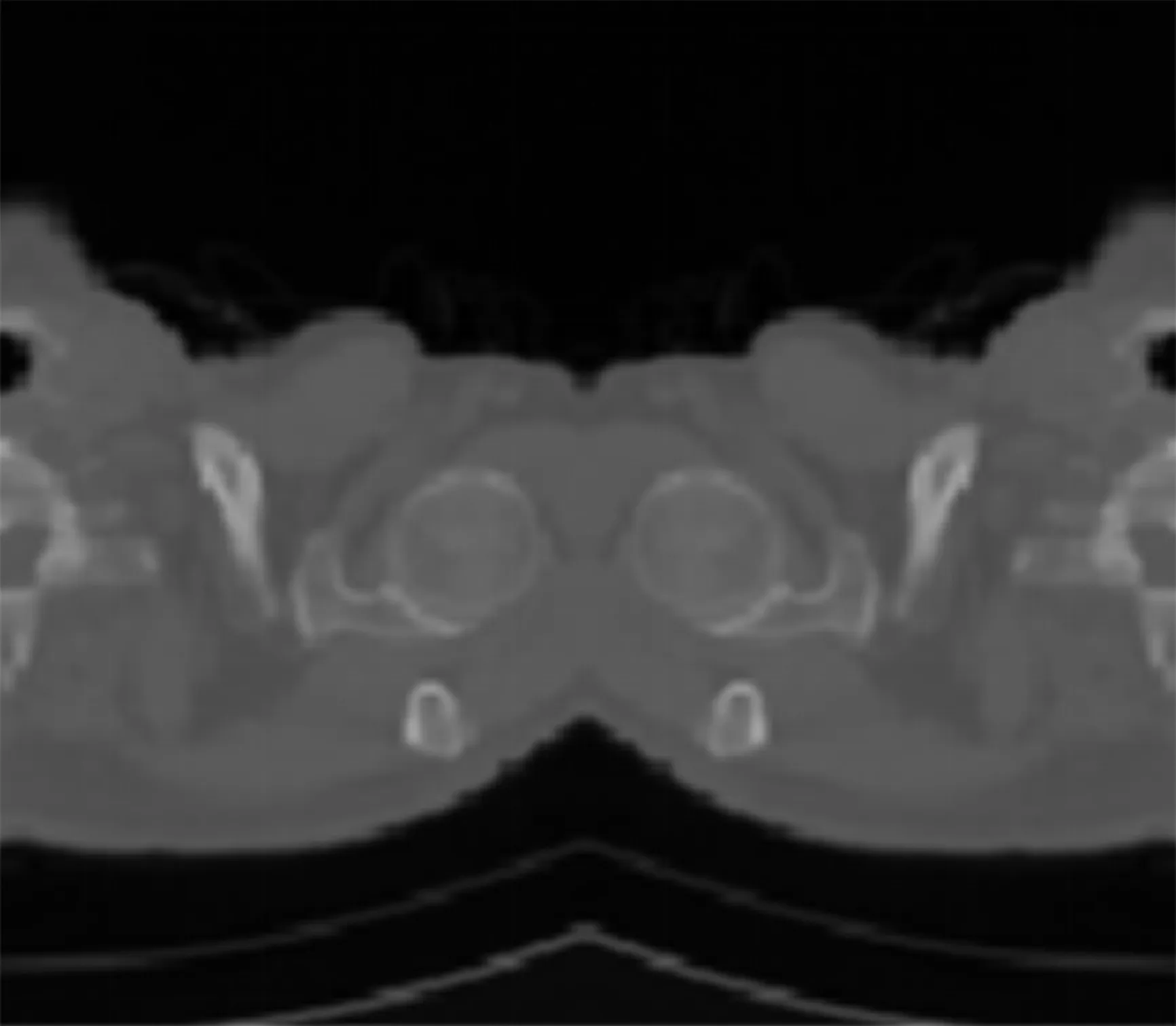
图4 CT图像切片Figure 4. CT image slice

在计算重建均方根误差式时，相应的Di为像素的真值，Ci为像素的重建值。在无噪声的情况下，当投影角度的数量变化时，对于算法TV-GSR、TV、SART和SART-GSR，不同投影角度数量下的重建均方根误差对比曲线如图5所示。在有噪声的情况下，当投影角度的数量为8时，不同噪声强度比例下的TV和TV-GSR重建算法的重建均方根误差对比曲线如图6所示。

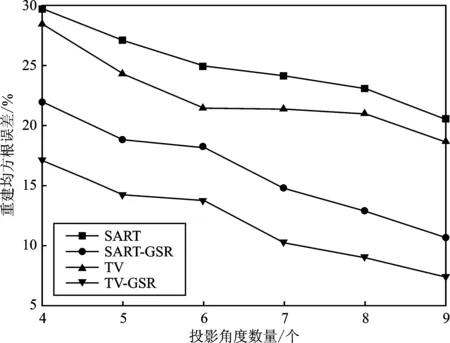
图5 无噪声情况下的重建均方根误差Figure 5. Reconstruction root-mean-square error in noiseless scenario

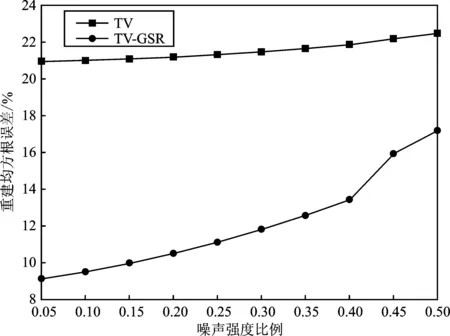
图6 有噪声情况下的重建均方根误差Figure 6. Reconstruction root-mean-square error in noisy scenario

从图5和图6可以看出，对于复杂CT图像，在无噪声和有噪声的情况下，GSR的加入不仅有助于客体重建精度的改善，还改善了客体的抗噪声性能。

从上述简单三维客体和复杂CT图像上的数值仿真可以看出，提出的TV-GSR算法同时考虑了客体图像的局部相似性和非局部自相似性，充分利用了图像的先验稀疏信息，提升了图像在无噪声和有噪声情况下的重建精度，对于高能闪光图像和纹理细节丰富的CT图像都有良好的效果，具有普适性。

5 结束语

持续提升闪光照相密度反演的精度是图像分析研究人员的努力方向。本文提出了一种基于GSR的TV重建技术(TV-GSR)，对TV算法模块和GSR 算法模块进行循环交替迭代，直到满足停止准则为止。本文采用上下对称性来降低分层重建的规模；采用左右对称性来降低GSR正则化的复杂度。通过仿真实验，定量给出了无噪声情况下投影图像数目和有噪声情况下噪声强度比例对密度重建精度的影响规律。基于纹理细节相对丰富的复杂CT图像的实验结果也证明了引入GSR有助于改善客体重建精度。本文提出的TV-GSR算法同时考虑了客体图像的局部相似性和非局部自相似性，提升了图像在无噪声和有噪声情况下的重建精度，对于高能闪光图像和复杂CT图像都有良好的效果，具有普适性。