SINS/BDS紧组合系统中自适应两阶段扩展卡尔曼滤波
臧中原,董 亮,毋 蒙,蒋 凯,杨 健
(上海航天控制技术研究所,上海 201109)
0 引言
为获得更高精度的定位结果,将多种导航定位技术组合,已成为导航定位的热门研究方向。捷联惯性导航系统(Strap-down Inertial Navigation System, SINS ) 是一种自主导航系统,具有短期精度高、自主性强、抗干扰能力强、数据更新率高等特点,可提供丰富的导航信息(包括位置、速度、姿态),缺点是其误差随时间累积,不适用于长时间单独导航。作为最主要的全球卫星导航系统( Global Navigation Satellite System , GNSS )之一,北斗卫星导航系统( BeiDou Navigation Satellite System , BDS )已全面建成[1]。BDS具有无累积误差和长期稳定性, 但易受干扰,接收机数据更新率低,无姿态信息。因此,为了提高系统的导航性能,将BDS和SINS两种系统融合,取长补短,充分发挥各自的优势,同时提高系统的导航精度。相较于采用位置/速度组合的SINS/BDS松组合导航系统,采用BDS接收机更原始信息—伪距/伪距率组合的SINS/BDS紧组合导航系统,具有更高的导航精度和可靠性。
在SINS/BDS组合导航系统中,由于未知随机常值偏差(如陀螺零偏、加速度计偏值、BDS接收机钟差等)的存在,已知该组合建立的非线性系统模型不准确和噪声不确定,从而导致滤波器的性能下降,甚至导致滤波器发散。为此,需要对系统状态和偏差进行同时估计,文献[2-3]将偏差项增扩为状态,提出了增广状态卡尔曼滤波器(Augmented State Kalman Filter,ASKF),增加了系统的维数,造成计算量增大、估计时间加长,从而影响滤波器的实时性,而且容易发散。针对线性系统的上述问题,B. Friedland和M. B. Ignagni相继提出了两阶段卡尔曼滤波(Two-stage Kalman Filter,TKF)算法及其改进算法,将状态与偏差分为两个卡尔曼滤波器进行估算,再利用偏差对状态进行修正。该算法适用于偏差项较多的情况,它能减少系统的状态维数,从而减少计算量,提高解算速度,并且不影响定位精度。此外,一些学者将TKF算法推广到非线性系统中,提出了两阶段扩展卡尔曼滤波器(Two-stage Extended Kalman Filter,TEKF)[4]和二阶段H∞滤波[5]。TEKF的实现过程与EKF[6]相似,都需要准确已知先验信息。然而在实际情况下,系统模型参数与实际物理过程有一定的偏差,系统的偏差与噪声方差以及量测噪声方差无法事先确定。所以,本文提出了一种自适应两阶段扩展卡尔曼滤波(Adaptive Two-stage Extended Kalman Filter,ATEKF)算法,即利用估算的几何精度因子(Geometric Dilu-tion of Precision,GDOP)值和新息对TEKF中的量测噪声方差进行在线估计的自适应滤波方法,并应用到SINS/BDS紧组合导航系统中,通过实际系统验证了该自适应算法的有效性。
1 SINS/BDS紧组合系统模型
1.1 状态方程
惯性导航系统选取东北天地理坐标系作为导航坐标系,记为n;载体坐标系记为b,其x沿载体横轴向右,y沿载体纵轴向前,z沿载体竖轴向上。组合系统的状态方程如下[7]。
假设SINS/BDS组合导航系统,SINS的误差模型具有下列形式

(1)
其中,状态向量
偏差向量
系统噪声向量
偏差噪声向量


1.2 量测方程



(2)

2 自适应两阶段卡尔曼滤波
2.1 两阶段卡尔曼滤波
将式(1)、式(2)合在一起构成组合系统的状态方程和量测方程[8-9],写成下列离散化式

(3)


考虑到SINS/BDS紧组合导航系统的状态方程是线性的,且式(3)非线性系统的信息完全已知,TEKF的耦合差分方程如下
(4)

无偏差状态估计方程为
(5)

类似地,偏差状态估计方程为
(6)
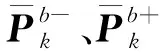
(7)
2.2 紧组合系统中的GDOP估算方法
在SINS/BDS紧组合导航系统中,以往求解GDOP值通常利用BDS接收机的定位结果。但在实际应用中,由于可见卫星的变化,会造成选星过程的重复,从而增大了计算量,使运算的时间成本增加,影响求解GDOP值的实时性。针对这种不足,本文提出了利用修正后的SINS的位置,并结合卫星位置估算GDOP值,从而完成选星过程。参考文献[7]的2.1节和文献[10]的5.4节中求解GDOP的方法,使用经过修正后的SINS的位置,将伪距观测方程由下式
ρ-r0=AX+V
转换为
ρ-rI=AIX+V
相应的几何矩阵AI表示为

则以修正后的SINS位置求得的几何精度因子定义为GDOPI,可以求得
(8)
这里可见卫星数选为4颗。在组合导航系统中,经过修正后的SINS位置误差较小,因此可以使用修正后的SINS位置输出求解GDOP,进而完成选星。该方法充分利用了组合导航系统中的已知量,显著缩短了选星时间。
2.3 量测噪声方差阵在线估计



(9)

(10)


已知,观测量的误差εδρ与位置误差、钟差的误差ΔX=[εδx,εδy,εδz,εδtu]T之间的关系式
ΔX=(ATA)-1ATεδρ
(11)

由于
E(ΔXΔXT)=(ATA)-1E(εδρ(εδρ)T)=σ2GI
再结合式(11)可得

(12)

进一步,由式(10)和式(12)可得
对于伪距率观测误差方差与速度误差和钟差率误差的估计方差同样存在上述关系式。
此外,通常SINS导航解算出的位置和速度,分别是在大地坐标系和地理坐标系下的。因此,在对量测噪声方差阵Rk进行估计之前,需要将权系数矩阵GI由ECEF坐标系转换到大地坐标系下,记为GI,λLh,产生相应的精度因子为GDOPI,λLh;或由ECEF坐标系转换到地理坐标系下,记为GI,ENU,产生相应的精度因子GDOPI,ENU。具体表达式如下
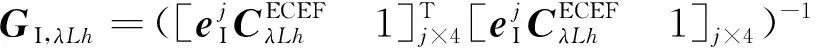

其中:Rk(·)表示伪距和伪距率对应的量测噪声方差阵中的相关项元素; tr(·)表示大地坐标系和地理坐标系对应的权系数阵对角线元素之和。

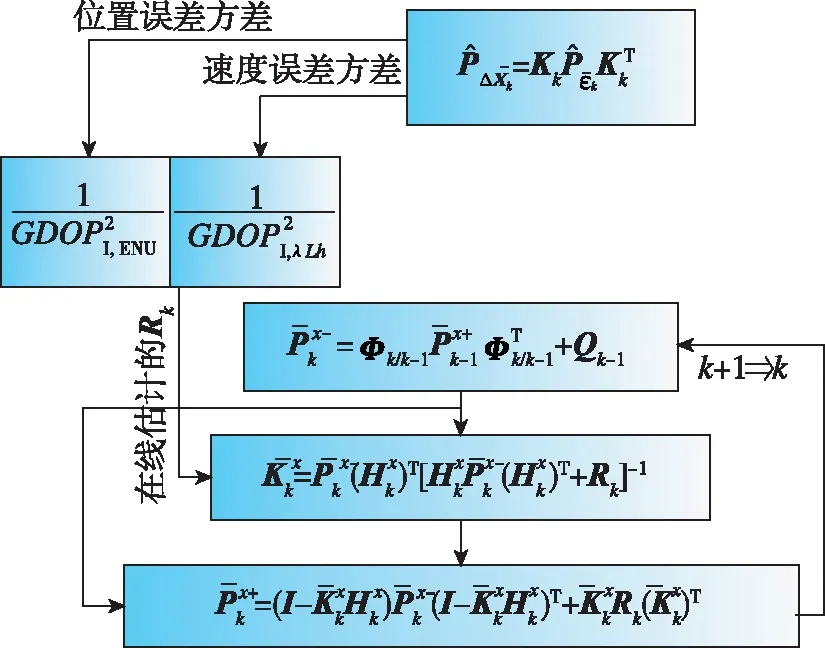
图1 自适应TEKF的流程图Fig.1 Flow chart of the ATEKF
3 仿真验证
为了验证本文提出的基于ATEKF的SINS/BDS紧组合导航算法的正确性和有效性,进行了跑车数据离线仿真实验。将本文提出的ATEKF的SINS/BDS紧组合导航算法与传统卡尔曼滤波的SINS/BDS导航方法进行离线仿真,对定位、测速精度作比较。
首先,在进行跑车实验的过程中采集BDS接收机数据和惯性测量数据,陀螺仪和加速度计的数据2.5ms存储一次,BDS接收机数据100ms存储一次。跑车试验过程中的惯性测量单元(Inertial Measure-ment Unit,IMU)和BDS接收机的参数设置为:陀螺零偏2(°)/h(1σ),零偏稳定性2(°)/h(1σ);加速度计零偏0.5mg(1σ),零偏稳定性1×10-4g(1σ)。BDS接收机位置误差为10m(1σ)、速度误差为1m/s(1σ);钟差和钟漂分别取30m(1σ)和0.3m/s(1σ);伪距和伪距率初始误差取1m(1σ)和0.5m/s(1σ)。跑车实验实物图如图2所示,Google地图显示的跑车实验二维轨迹如图3所示。用跑车实验中采集的离线数据进行离线仿真实验,实验时长为700s,实验结果如图4和图5所示。

图2 跑车实验实物图Fig.2 Picture of vehicle experiment

图3 基于MATLAB显示的SINS/BDS组合导航跑车轨迹Fig.3 The vehicle track of SINS/BDS integrated navigation system on MATLAB

图4 紧组合导航系统位置曲线比较Fig.4 Comparison of position curves in tightly integrated navigation system

图5 紧组合导航系统速度曲线比较Fig.5 Comparison of velocity curves in tightly integrated navigation system
在图4和图5中,蓝线表示传统方法的仿真曲线,红线表示本文方法的仿真曲线。从仿真结果可以得出:本文方法的精度优于传统方法;位置和速度误差都有改善,曲线较为平滑,误差减小,导航效果稳定。传统方法和本文方法的误差比较如表1所示。

表1 传统方法和本文方法的误差比较
4 结论
本文结合新息和估算的GDOP值,对量测噪声方差阵Rk进行在线估计,从而实现了自适应TEKF。仿真实验结果表明,该方法具有较好的效果,速度误差和位置误差均明显减小,系统的精度得到了明显提高,滤波稳定性也得到了改善。最后,通过采集跑车实验数据,对本文中设计的ATEKF的SINS/BDS紧组合导航系统进行了离线仿真实验验证,相较于传统方法,定位测速精度均得到提高。

