基于信任域策略优化的末制导控制量学习算法

刘士荣，王天一，刘 扬

(哈尔滨工业大学计算学部，哈尔滨 150001)

0 引言

近年来，随着深度学习的崛起，深度强化学习被广泛研究，涌现出了许多优秀的强化学习算法，在游戏[1]、机器人控制任务中取得了出色的表现[2]。无模型强化学习算法在智能体与环境的不断交互中采集数据学习策略，一般有两种方法：值函数迭代法和策略梯度法。值函数迭代法通过学习状态动作值函数来隐式学习一个确定性的策略，而策略梯度法显式建模策略分布，通过计算策略梯度不断学习出好的策略分布。值函数迭代法中，最广为人知的便是DeepMind公司开发的深度Q学习(Deep Q-Learning，DQN)[3]算法，其将深度学习与Q-learning算法相结合，使用神经网络自动学习图像这种高维输入的低维表示，并且可以端对端的训练，是第一个可以在雅达利游戏中接近人类水平的人工智能体。DQN还有一系列变体，如缓解DQN中值函数过估计的Double DQN[4]，用于连续动作空间的深度确定性策略梯度(Deep Deterministic Policy Gradient，DDPG)[5]、缓解DDPG中值函数过估计的TD3[6]算法等。幕上的反向更新(Episodic Backward Update，EBU)[7]在整个幕上采样，并连续将状态的值传递到前面的状态，优先经验回放(Prioritized Experience Replay，PER)[8]根据优先级选择训练样本，可以显著提高DQN算法的采样效率，事后经验回放(Hindsi-ght Experience Replay，HER)[9]算法可以高效解决稀疏奖励问题。由于策略梯度法可以显式建模策略分布，更天然地适用于连续动作问题，通常在机器人控制等连续动作问题中被广泛使用，但需要一些技术来降低策略梯度的方差。最直接的策略梯度算法为REINFORCE[10]，信任域策略优化(Trust Region Policy Optimization，TRPO)[11]为了让策略能够稳定提升，显式增加了一个约束，限制每次策略更新的最大偏移量，可以提高策略梯度法学习过程中的稳定性。为了平衡优势函数的偏差和方差，还使用了广义优势估计器(General Advantage Estimation，GAE)[12]。进化策略(Evolution Strategy， ES)[13]通过突变操作改变原始参数，并检验改变后参数的效果，保留那些结果较好的进化策略类似于神经进化和直接策略搜索，在搜索过程中没有使用梯度信息，本质上相当于在使用奖励函数作为启发式函数在参数空间中直接进行搜索。

在末制导领域中，比例制导律[14]是很常见的方法，在理想条件下有很好的表现，但其导航比是一个常数，无法为每个状态自适应地调整该比率，很难适应复杂环境。文献[15]使用Q-learning学习比例系数，文献[16]使用DDPG算法学习制导策略，文献[17]也使用DDPG算法通过优化导航比来学习末制导律，学习比例制导律中的导航比，算法效果优于比例制导律；但其实验环境相对简单，没有考虑空气动力学，其作者发现在考虑空气动力学的环境中会有训练不稳定的问题。本文方法关注末制导策略的在线学习，在导弹与目标在仿真环境的在线交互过程中，直接学习末制导控制量，即不借助已有末制导律，直接为导弹提供加速度，并在考虑空气动力学的环境中进行实验，实验结果表明，本文提出的方法在提升训练稳定性的同时也学习到了高效的策略。

本文第1章介绍了强化学习算法的基本原理，包括强化学习算法概述、策略梯度算法及信任域策略优化算法的原理与推导；第2章介绍了本文的实验部分，首先给出了强化学习末制导问题的模拟环境，以及如何将信任域策略优化算法应用到末制导控制量的学习中，介绍了马尔可夫模型中的状态空间设计、动作空间设计以及奖励函数设计；在实验部分又找到两个强化学习算法作为基准，分别是EBDQN算法和ES算法，然后将本文提出的奖励函数与另外两种奖励进行对比，同时给出实验对比结果；最后，在第3章对本文的工作进行了总结。

1 强化学习算法介绍

1.1 强化学习概述

序列决策问题通常被形式化为马尔可夫决策过程(Markov Decision Process，MDP)。MDP定义为一个六元组(S,A,T,r,γ,ρ0)，S为状态空间，A为动作空间，T:S×A×S→R为状态转移概率，r:S×A→R为奖励函数，γ∈(0,1)为折扣因子，ρ0:S→R为初始状态分布。

强化学习考虑智能体在与环境交互过程中学习到能够最大化奖励的行为。在每个时刻t，智能体处在状态st∈S下，根据自己的策略π:S×A→[0,1]选择一个动作at∈A，然后得到奖励rt，并进入下一个状态st+1∈S。

(1)

其中，at～π(·|st),st+1=T(st,at)。强化学习的目标是找到一个最优策略π*，使得期望回报最大，即π*=argmaxπJ(π)。为了便于学习策略，定义状态值函数

(2)

以及状态动作值函数

Q(s,a)=

(3)

1.2 策略梯度法

策略梯度法[10]通过计算目标函数在策略参数处的梯度，得到策略的更新方向，用π(θ)表示待学习的参数化策略，θ为策略参数，则策略梯度法的目标函数如下

J(θ)=Et[logπθ(at|st)*A(st,at)]

(4)

其中，A(st,at)=Q(st,at)-V(st)，为t时刻的优势函数。策略梯度法的主要问题是估计得到的梯度有很大方差，容易造成策略崩塌，影响训练稳定性。

1.3 信任域策略优化算法

信任域策略优化[11]算法在策略梯度法的基础上加入了一个用来限制策略偏移的约束，以避免策略偏移带来的梯度偏差所引发的策略崩塌，使得学习过程更加稳定。信任域策略优化算法的优化问题如下

(5)

Et[DKL(πθ(at|st)||πθold(at|st))]≤δ

(6)

其中，πθold表示采样策略；θold表示采样策略的参数；Et表示采样策略πθold采集到的每个时刻样本下的期望；DKL表示KL散度；δ是一个超参数，表示策略偏移的最大幅度。

为了求解该优化问题，对目标函数和约束项分别做一阶、二阶泰勒近似，得到如下近似优化问题

maxθJ(θold,θ)≈gT(θ-θold)

(7)

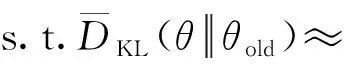
(8)

其中

(9)

(10)

该近似优化问题可求出最优解

(11)

近似优化问题虽然有最优解，但不一定是原问题的最优解，故信任域策略优化在此基础上还做了线搜索(line search)，将近似优化问题求得的最优解作为最大步长进行指数衰减线搜索，找到可以真正优化原始目标函数的步长。令α为指数衰减速度，j为搜索次数，则得到如下参数更新公式

(12)

信任域策略优化算法需要计算KL散度的Hessian阵，是一种二阶优化算法，需要一些代码上的优化来加速求解，如费雪向量积和共轭梯度法。同时，信任域策略优化算法使用了GAE估计优势函数，可以权衡优势函数估计器的偏差和方差。此外，二阶优化算法也意味着信任域策略优化更适合低维问题，在高维问题中会面临Hessian阵估计不准、计算量大的问题，从而影响算法训练效果和训练速度。末制导问题的状态维度和动作维度都比较低，故本文将信任域策略优化算法应用到末制导控制量的学习中，使策略的学习变得更加稳定，提升习得策略的表现。信任域策略优化算法的伪代码如表1和表2所示。

表1 算法整体流程

表2 信任域策略优化算法

2 使用信任域策略优化算法学习末制导控制量

2.1 仿真环境建模

为了将强化学习算法应用于末制导问题中，需要对实际制导问题进行仿真模拟。导弹作为一种高速飞行的打击武器，通常应用于远距离打击范围任务中，在这种情况下，导弹与目标本身的尺寸可以被忽略，只关注二者的相对位置关系即可，即将导弹与目标简化成为两个质点。

将制导问题应用在真实的三维环境中，经大量的研究显示，三维空间的仿真建模复杂且计算量太大。文献[18]的研究结果表明，二维空间与三维空间中的运动存在相似性，可以通过降维等手段将三维空间的运动问题分解成两个相互正交的二维平面中的运动问题。

本文的导弹-目标仿真环境建模即采用上述的思想，选择在二维平面内对末制导问题进行仿真环境建模，并基于质点模型，忽略了导弹和目标双方的机身尺寸，整个拦截场景处于惯性参考系下，仿真场景如图1所示。其中，M与T分别表示导弹与目标质点；θM与θT为导弹和目标的弹道倾角；q与r为视线角与弹目相对距离；aM与aT为控制导弹和目标转向的法向加速度。整个仿真过程遵循如下运动学公式

(13)

(14)

(15)

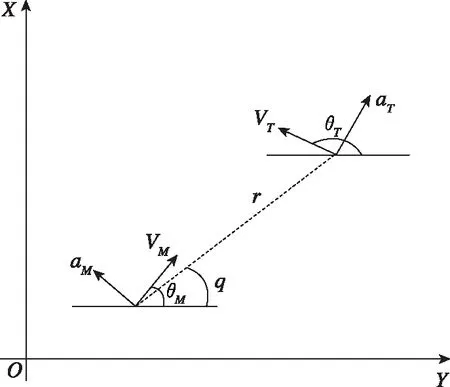
图1 仿真场景示意图Fig.1 Schematic diagram of simulation environment

此外，在真实环境下，考虑到传输噪声对弹头指挥部的制导系统可能会产生的干扰，以及空气动力学所产生的各种噪声(如空气密度不同带来的声速不同进而影响到拦截弹飞行的情况)，本文在本次仿真环境中额外加入对于噪声的考量。首先，由于不同高度下空气的密度和声速是不同的，因此在这里首先对给定高度下的空气密度和声速进行计算，具体方式如下：

1)位势高度计算：本次仿真模型均设定在标准大气压下。首先计算在给定目标高度下的位势高度

(16)

其中，r0为地球半径，取6356766m;yM为弹体或者目标的纵向高度，单位为m。

2)实时摄氏温度计算：此处取常压下地面温度15℃，由热力学温度转化公式可知地面热力学温度为288.25K，据此计算给定高度的摄氏温度如下

T=Tb+cT×(Z-Zb)

(17)

其中，Tb为热力学温度；cT为一衰减系数，由高度与温度变化关联公式可知，高度每升高1000m气温降低6.5℃，即设定为-6.5×10-3；Zb为扰动系数，此处取0.0。

3)空气压力计算：已知给定温度，即可计算定高度下的空气气压，其计算公式如下

(18)

其中，Pb为标准大气压下的毫米水柱，取值为10332.3mm H2O；g0为重力加速度，取值为9.80665；cP为干燥空气的摩尔气体常数，通常取287.05287。

4)空气密度计算：在已知空气压力的情况下，空气密度可由式(19)求得

(19)

5)声速计算：声速计算公式在已知摄氏温度的情况下可以根据式(20)求得

(20)

单位为m/s。

在不同的空气密度和声速下，模型的气动参数也是不停变化的。不同的气动参数会影响导弹的一阶特性与二阶特性，进而影响到导弹的实时速度。此处假定导弹速度的初始变化率为-25m/s，结合导弹的特征面积，给出导弹受空气密度噪声影响的速度变化公式如下

Vdot=

(21)

其中，CD、CK、CLafa均为气动参数;α为攻角指令，由过载指令结合空气密度计算而来；ρ为前述空气密度；VM为导弹的实时速度；Sxsf为导弹的特征面积，一般取0.2；m为导弹质量，此处取m=400kg；θm为导弹的弹道倾角。此外，为增加算法的鲁棒性，本文对于环境中也施加了部分随机噪声，具体方法如下：通过对导弹运动的角噪声进行处理，从而对视线转率施加噪声，进而影响视线转率的二阶特性，使得训练更具有普遍性，减小因过拟合带来的误差。由上述公式，即式(16)～式(21)，可以考虑真实战场下的空空攻防战空气噪声参数，从而实现更加普遍、通用、包容性强的算法模型。

2.2 MDP建模

2.2.1 状态空间设计

在实验中，将智能体的状态定义为一个8维向量，前4维分别表示导弹和目标双方的坐标在X坐标轴和Y坐标轴方向的分量，后4维分别表示导弹和目标双方的速度在X坐标轴和Y坐标轴方向的分量。

s=(XM,YM,XT,YT,VM,X,VM,Y,VT,X,VT,Y)

(22)

2.2.2 动作空间设计

将智能体的动作定义为一个标量，表示提供给导弹的加速度，是一个连续的值。动作的取值范围通过超参数A_MAX设置，在实验中将其设置为300。

at∈(-A_MAX,A_MAX)

(23)

2.2.3 奖励函数设计

奖励定义为上一时刻的预测脱靶量与当前时刻的预测脱靶量的差值，表示当前时刻动作对预测脱靶量的降低量

rt=-1*(zemt-zemt-1)

(24)

其中，zemt为t时刻的预测脱靶量，是导弹和目标相对距离的最小值的预测值，计算公式参考文献[18-19]。直观上说，预测脱靶量是以导弹为参照系，导弹相对静止，而目标在进行匀速直线运动，目标不断运动直到与导弹的距离达到最近，此时的距离称为预测脱靶量。可见，与当前时刻双方的相对距离不同，预测脱靶量的计算考虑了导弹和目标的实际运动情况。但预测脱靶量只考虑了导弹和目标当前时刻的相对速度，没有考虑它们在未来时刻的速度变化，是对实际脱靶量的近似估计，而实际脱靶量是不可能精准预测的，所以本文采取这种简单的方法，通过预测脱靶量来近似估计实际脱靶量，进而计算奖励。

上述MDP建模尽量少地使用末制导领域专业知识，只使用位置和速度这些简单易懂的量作为状态，动作也是直接为导弹提供的加速度，没有制导律相关知识，更能验证强化学习在末制导领域应用的潜力。如果使用末制导领域专业知识来设计状态和奖励，可能会提升算法的表现和泛化性，但降低了设计的通用性，所以本文决定采取这种简单有效的MDP设计。

2.3 算法超参数设置

TRPO算法具体超参数设置如表3所示，环境中导弹和目标的初始参数如表4所示。

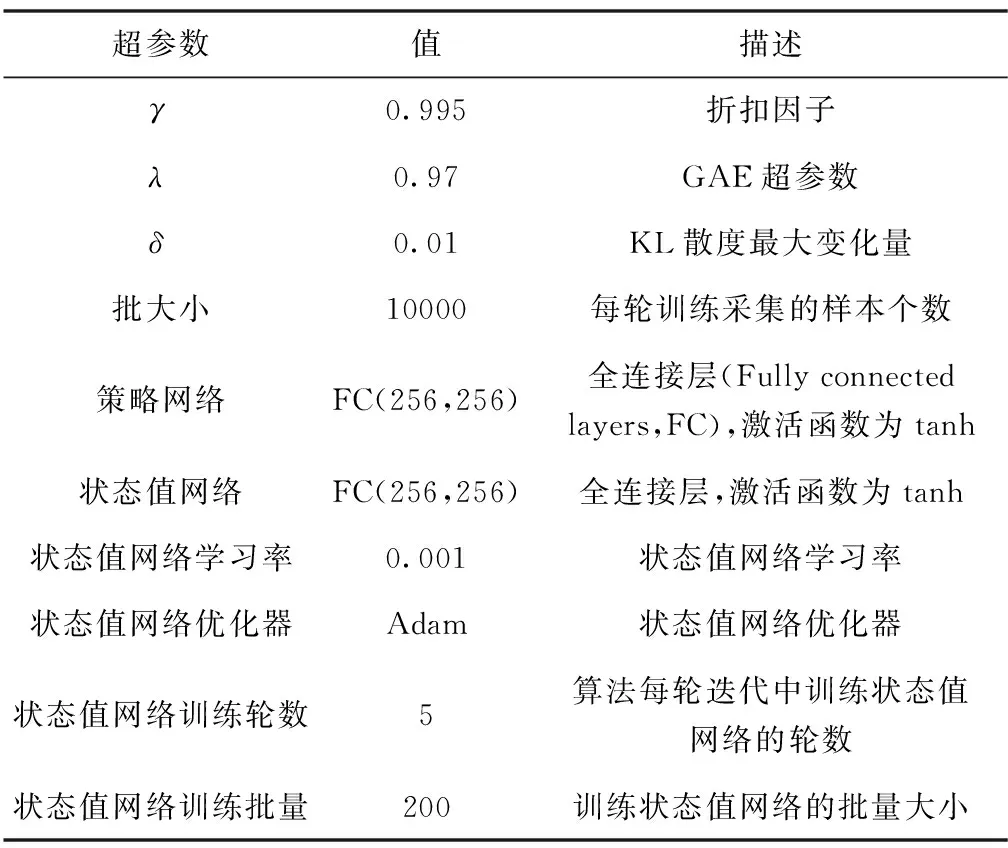
表3 TRPO算法超参数

表4 导弹和目标初始的参数

2.4 实验结果与分析

为了验证本文提出的算法的高效性能，对比了其他两种强化学习制导律算法，分别是基于进化策略的ES算法和基于EBDQN的自适应导航比末制导律算法[20]。ES算法使用进化算法直接优化策略，EBDQN算法通过从经验回放池中采样整个轨迹，并从结束状态从后向前更新值函数，可以提高样本的使用效率。

在2.1节介绍的仿真环境中，在2.2节介绍的MDP设置下，基于表3所示的TRPO算法超参数与表4所示的导弹和目标的初始参数，使用TRPO算法学习末制导控制量，测试脱靶量，与直接学习末制导控制量的ES算法和学习引导率参数的EBDQN算法相比，其脱靶量累积分布图如图2所示。在图2中，横轴为脱靶量大小，单位为m，纵轴为累积分布概率，实验重复次数为500次，脱靶量分布结果如表5所示。可以看出，同是直接学习末制导控制量的TRPO和ES算法，TRPO算法的脱靶量比ES算法更低，而且TRPO算法的脱靶量优于学习引导率导航比参数的EBDQN算法，说明TRPO学习到的控制量比引导率的效果更好，在复杂场景中直接学习控制量的方法有希望超过学习引导率的方法。

图2 脱靶量累计分布Fig.2 Cumulative distribution of miss distance

表5 制导律脱靶量分布

此外，本文将在线强化学习算法应用于末制导控制量的学习中，由于末制导常常强调机动性，故需要通过实验测试算法的响应时间，即智能体做出决策所需要的时间。表6展示了三种强化学习算法的响应时间，单位为ms，实验运行环境为i5 7300HQ CPU，16G内存，没有用到 GPU。可以看到，三种算法的响应时间都是ms级的，响应都很快速，这是因为它们的策略网络和值网络都是简单的全连接层，参数较少，计算时间短。

表6 三种算法的响应时间

2.5 实验对比不同的奖励设计方法

在强化学习中，奖励承担着重要的作用，它负责传递这一次动作的奖惩情况，智能体根据奖励的变化进行策略的优化。本节通过实验对比不同的奖励函数，包括稀疏奖励、朴素奖励以及本文提出的新颖奖励，从而验证本文所提的奖励函数的高效性。

首先介绍稀疏奖励。在末制导的实际物理环境中，只有当导弹命中目标时，才会收到命中的奖励，其他时间无论导弹怎么改变方向、调节速度，在命中之前都不会获得任何奖励，这种奖励函数是一个典型的稀疏奖励。将其设计为式(25)，当一条轨迹最终距离目标小于5m时，给予10的奖励，其余时刻全都是0的奖励。然而，稀疏奖励问题会导致强化学习算法收敛缓慢，甚至是无法收敛。

(25)

朴素稠密奖励函数是最符合人类直觉的一种奖励，将导弹与目标之间的距离作为衡量奖励的尺度，距离目标越近，则给出越大的奖励，距离目标越远，则给出越小的奖励。奖励的具体形式如式(26)所示，在每一时刻，将导弹与目标之间距离的负数作为奖励。然而，这种负奖励会促使智能体尽早结束轨迹，影响策略学习。

(26)

为了解决在末制导环境中的稀疏奖励问题以及朴素稠密奖励的学习效率低下的问题，提出了一种创新性的奖励函数设计。将奖励定义为上一时刻的预测脱靶量与当前时刻的预测脱靶量的差值，表示当前时刻动作对预测脱靶量的降低量，关于该奖励的更详尽的介绍请参考2.2.3节式(24)。

为了说明本文设计的新颖奖励函数的高效性，图3对比了与三种奖励函数在相同实验环境下训练时的脱靶量变化曲线，横轴为训练轮数，共训练500轮，纵轴为每一轮训练后的脱靶量，单位为m，每轮测试次数为5次。可以发现，本文提出的奖励函数能够使训练更稳定，并且能达到更低的脱靶量。

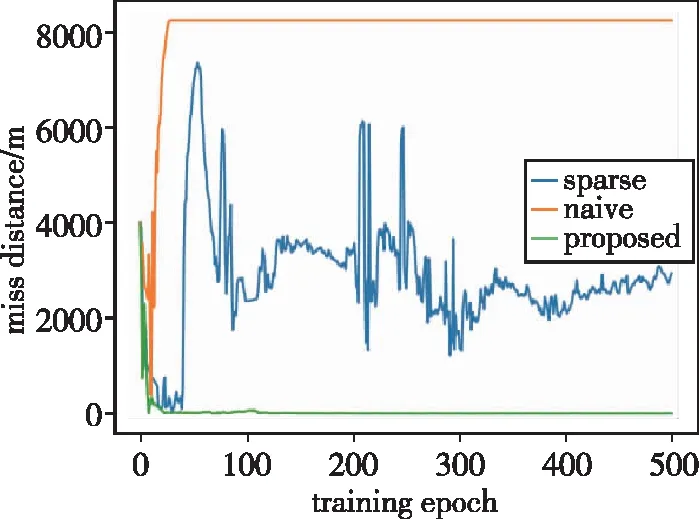
图3 三种奖励在训练时的脱靶量变化曲线Fig.3 Curves of miss distance of three rewards during training

3 结论

1)本文将TRPO算法应用于末制导问题，在与环境交互的过程中直接学习末制导控制量，而非学习末制导律中的参数，有助于发现更优的制导策略。设计了简单的状态，避免引入末制导专业知识，并设计了一种新颖的奖励函数，该奖励函数考虑了导弹和目标的运动情况，更适合末制导问题。仿真环境中考虑了空气动力学，更接近真实场景。

2)实验结果表明，通过使用本文算法和提出的奖励，智能体学到的控制策略可以达到更低的脱靶量，命中效果更好。

3)本文只在仿真环境中进行实验，使用强化学习算法在真实场景中进行控制量学习是未来有价值的研究方向。