基于T-S模糊模型的非线性分布参数系统极点配置P-sD控制
党爱然,栾秀春,孙贺涛,王俊玲,周 杰,杨志达
(1. 哈尔滨工程大学黑龙江省核动力装置性能与设备重点实验室,哈尔滨 150001;2.哈尔滨工程大学核安全与先进核能技术工信部重点实验室,哈尔滨 150001;3.哈尔滨工程大学核安全与仿真技术国防重点学科实验室,哈尔滨 150001)
0 引言
分布参数系统是一种由偏微分方程、泛函微分方程及偏微分-积分方程等多种形式组成的系统,在物理学中,很多现象都是用偏微分方程来描述的,这些现象的控制问题也具有很强的现实背景。分布参数系统广泛应用于热工、导弹、航空及核裂变等工程系统,并且分布参数系统的稳定性对于设计控制器也起到至关重要的影响。另一方面,由于非线性问题在实际工程中普遍存在,国际上对非线性系统的控制设计问题进行了大量的探讨。其中,模糊控制技术,尤其是Takagi-Sugeno(T-S)模糊控制技术在非线性系统的分析和解决综合问题时得到了广泛应用,因为这种控制技术具有同时兼顾模糊逻辑理论和线性系统理论的优点。
在国际上,有关非线性分布参数系统的稳定性分析和控制器设计方面成果颇丰,可是已有的一些方法在某些情况下仍然存在问题,有待进一步改进与创新。采用T-S模糊模型描述非线性分布参数系统,并以此为基础设计P-sD状态控制器是一种较为新颖的设计方式,此种方式既有较强的创新性,又能同时兼顾系统的稳定性,在实际设计中有着较强的实际意义。
分布参数系统的稳定性对于设计控制器非常重要,各国学者在此方面做了很多研究。文献[1]研究了非线性分布参数系统在平衡状态时的局部指数稳定;文献[2]针对具有特定边界条件的非线性分布参数系统的稳定性进行了证明;文献[3]对分布参数系统设计了反馈控制器,并验证了引入控制器后整个系统的稳定性;文献[4]不仅证明了分布参数系统的稳定性,同时证明了分布参数系统的能控能观性;文献[5]基于鲁棒性,针对非线性分布参数系统设计了观测器;文献[6]研究了非线性分布系统的渐进稳定性和同步性,提出了一个新分布引理,并给定了几个充分条件和数值算例,以证明该分布模型的渐进稳定性和同步性。在文献[7-9]中均提出了将分布参数系统视为无穷维系统的思想,即将算子与状态函数视为无穷维矩阵与向量,文献[10]还依据这样的思想来证明分布参数系统的能控性与稳定性。将分布参数系统视为无穷维系统的思想可以将分布参数系统与集中参数系统进行类比,文献[11]中采用Lyapunov方法来证明系统的稳定性。
在系统稳定性分析方面,降阶建模是一种十分有效的手段,国内外学者在降阶建模基础上的研究与创新成果颇丰。在验证系统稳定性方面,线性分布参数系统相比非线性分布参数系统更加容易验证,所以文献[7-8]中提出了将非线性分布参数系统降阶建模的理念。文献[12]提出了一种新的低阶时空最小二乘支持向量机方法对非线性分布新系统进行建模,并提出了一种基于核空间的空间相关分析方法;文献[13]针对具有马尔可夫跳变执行器故障的非线性分布参数系统的事件触发有限时间可靠控制问题,提出了采用T-S模糊模型描述所考虑的非线性分布系统,采用一种新的事件触发策略调节采样数据的传输瞬间,并通过仿真研究验证了该方法有效性;文献[14]利用采样数据模糊控制方法,研究了一类非线性抛物型偏微分方程系统的指数稳定问题,通过对扩散方程和FHN方程的控制进行仿真,验证了提出设计方法的有效性;文献[15]提出了一种非线性度量方法,以量化分布系统的非线性严重程度;文献[16]回顾、讨论和比较了非线性测度的定义和计算方法,讨论了混合系统和由耦合微分、积分和代数方程描述的非线性测度的扩展。针对参数未知以及存在时滞的分布参数系统,通常采用参数辨识以及智能控制的方法进行设计。文献[17]提出了针对参数未知的分布参数系统进行状态估计;文献[18]采用迭代学习控制,针对系统参数变化的分布参数系统进行设计;文献[19]采用学习算法解决非线性分布参数系统的跟踪控制问题;文献[20]在参数未知的非线性分布参数系统中引入了神经网络的方法进行控制;文献[21]讨论了分布参数系统中参数辨识的一般问题,提出了一种基于量子引导跟随的变异策略优化算法作为优化策略;文献[22]研究了具有时滞的分布参数模型多智能体系统的一致性控制问题,提出了一种分布式P型迭代学习控制方法;文献[23]研究了线性不稳定分布参数系统的异常时空源检测与估计问题,基于空间域分解方法进行理论分析,并设计了相应的自适应控制;文献[24]研究了参数未知并且不确定分布的分布参数系统的跟踪控制问题;文献[25]针对非线性分布参数系统设计了鲁棒神经网络自适应控制器,采用智能控制方法中的神经网络,既满足了非线性分布参数系统的稳定性,又实现了参数不确定系统的自适应控制;文献[26]提出了当分布参数系统中输入是有限维的情况下,模糊控制仍然可以实现设计要求。
分布参数系统建模广泛应用于各类工程系统的设计与分析中。在现实的工程问题当中,分布参数系统十分普遍,在涉及传热以及振动等现象时,往往采用分布参数系统进行建模。因此,证明系统的稳定性和面临非线性以及参数未知等情况下的降阶建模及设计相应的控制器是十分重要的。文献[27]就核电站中蒸汽发生器的传热过程进行了分布参数建模,并以此为基础设计了符合需求的控制器;文献[28]就太阳能发电以及发热系统进行了分布参数系统建模,并对其中环节进行了参数调节方式的分析,以从中寻求降低成本与提高效率的方法。
本文从分布参数系统的稳定性着手,将非线性分布参数系统中的非线性项用T-S模糊方法建模,并根据此模型设计状态反馈控制。由于分布参数系统中存在空间一阶微分项与二阶微分项,在运用Lyapu-nov方法证明稳定性的过程中,Lyapunov函数的微分中将出现常数项与积分项。针对积分项,采用状态反馈的方法进行控制,根据配置空间极点函数来设计状态反馈,非线性分布参数系统中的非线性项采用文献[11]中的T-S模糊建模方法,以确保设计过程的顺利进行。T-S模糊建模将非线性项表达成在不同时刻线性项的组合形式,对分布参数系统的参数时空分离进行了讨论,在文献[29]中,有时空分离的方法能够提高建模精度的论述,在本文中引入的T-S模糊建模方法和原本的非线性分布参数系统是相同的。针对常数项,引入状态变量的空间一阶微分项,通过状态变量的边界条件进行计算,以抵消Lyapunov函数的微分中的常数项,文献[30]也提出了通过边界条件实现控制分布参数系统。这样引入状态反馈以及状态变量空间一阶微分项的控制方法,在文献[11]中被称为P-sD状态控制。与现有的P-sD状态反馈相比,通过考虑边界条件来消除影响,增强了极点配置对于性能的调节作用。
1 分布参数系统的稳定性
对于线性分布参数系统系统
A(x)Y(x,t)+B(x)U(x,t)
(1)
采用Lyapunov直接法讨论系统的稳定性。式中,Y(x,t)=[y1(x,t)y2(x,t) …yn(x,t)]T,x∈[l1,l2],y1…n(x,t)是闭区间[l1,l2]上的连续函数;Θ1(x)、Θ2(x)和A(x)是连续n×n矩阵函数;B(x)是连续n×1矩阵函数。
考虑Lyapunov函数

(2)
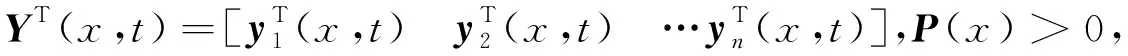
(3)
将式(1)代入式(3)中,得
B(x)U(x,t))dx
式中,积分项中分为四部分,其中包含空间二次微分项的第一部分采用分部积分法进行处理
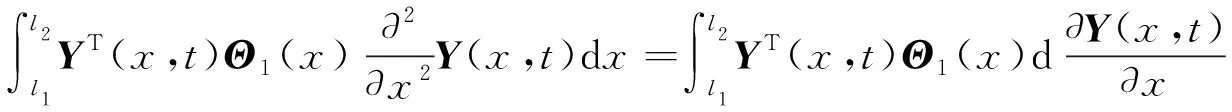
(4)
式中
(5)
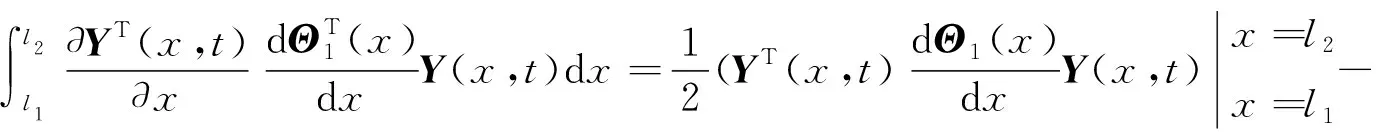
(6)
将式(6)代入到式(4)中,得
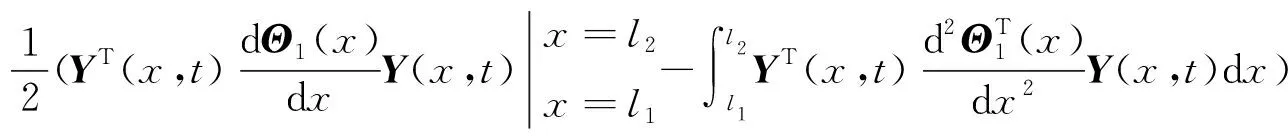
(7)
包含空间一次偏导项的第二部分仍然采用分部积分法进行处理
(8)
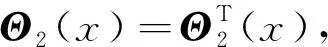
(9)
将式(7)与式(9)代入得


(10)
(a)
(b)
Y(x,t)dx
(c)

(d)
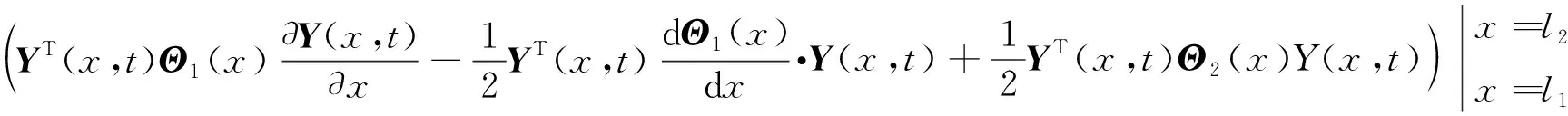
1)矩阵函数Θ1(x)为对称矩阵,且Θ1(x)>0;
2)矩阵函数Θ2(x)为对称矩阵;
3)矩阵函数P(x)=I(x),在此处是为了简便推导过程,其实矩阵函数P(x)为对称矩阵,且P(x)>0,则接下来的推导过程也成立。在这里,即使将P(x)选取为对角矩阵也不会增强结论的保守性。
2 控制器设计
设计合适的控制器保证系统的稳定性。根据式(10)中不同部分,采用对应的方法设计控制器。
2.1 极点配置
U1(x,t)=K(x)Y(x,t)
式中,K(x)为1×n维连续矩阵函数。

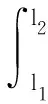
通过调节矩阵函数K(x),可以使F(x)+B(x)K(x)的特征函数λ(x)为指定的空间函数,满足系统的稳定性与符合性能要求。
2.2 P-sD状态反馈
式(10)中可以根据边界条件求出确切数值的部分,正负是不确定的。针对这部分采取的方法是在输入中引入状态变量的空间微分项,使这一部分的数值变为0,从而对整个系统的稳定性没有影响。

式中,L为1×n维实数矩阵,由此可得

在这里,B(x)L=LTBT(x)。所以

通过设计实数矩阵L,使

那么,引入设计好的控制器,输入U(x,t)为
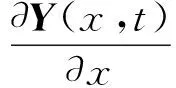
这是一种设计P-sD状态反馈控制的新思路。
3 T-S模糊模型
非线性分布参数系统中的非线性项表示为f(x,Y(x,t)),则非线性分布参数系统表示为
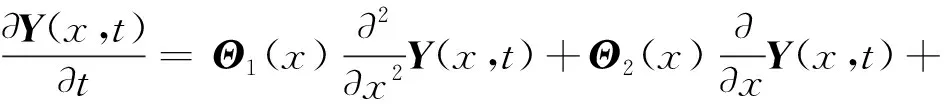
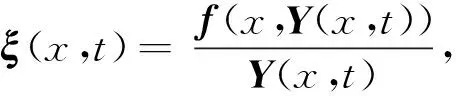
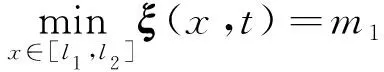
根据最大值与最小值,ξ(x,t)可以表达为
ξ(x,t)=h1(ξ(x,t))m1+h2(ξ(x,t))m2
式中,h1(ξ(x,t)),h2(ξ(x,t))∈[0,1],且h1(ξ(x,t))+h2(ξ(x,t))=1。
隶属度函数如图1所示。定义模糊集为“大”与“小”,那么非线性分布参数系统由如下规则的T-S模糊模型描述:
如果ξ(x,t)属于“小”,则
A(x)Y(x,t)+m1Y(x,t)+B(x)U(x,t)
如果ξ(x,t)属于“大”,则
A(x)Y(x,t)+m2Y(x,t)+B(x)U(x,t)
那么,非线性分布参数系统表示为
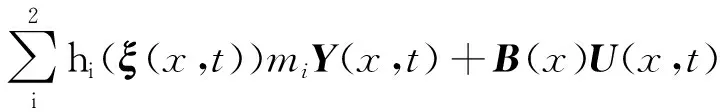
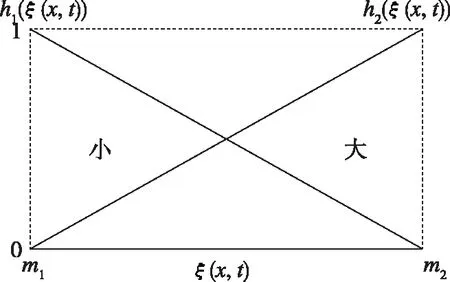
图1 隶属度函数Fig.1 Membership function
4 系统仿真结果及分析
对如下具有两个不同边界条件的具体的非线性分布参数系统设计控制器并进行仿真。控制器设计步骤为:


4.1 具有第一类边界条件非线性分布参数系统
受约束与一类边界条件,x∈[0,π],t≥0,y1(0,t)=0,y1(π,t)=1,y2(0,t)=0,y2(π,t)=1,初始条件,y1(x,t0)=sin(0.5x),y2(x,t0)=sin(0.5x)。
模糊T-S模型为
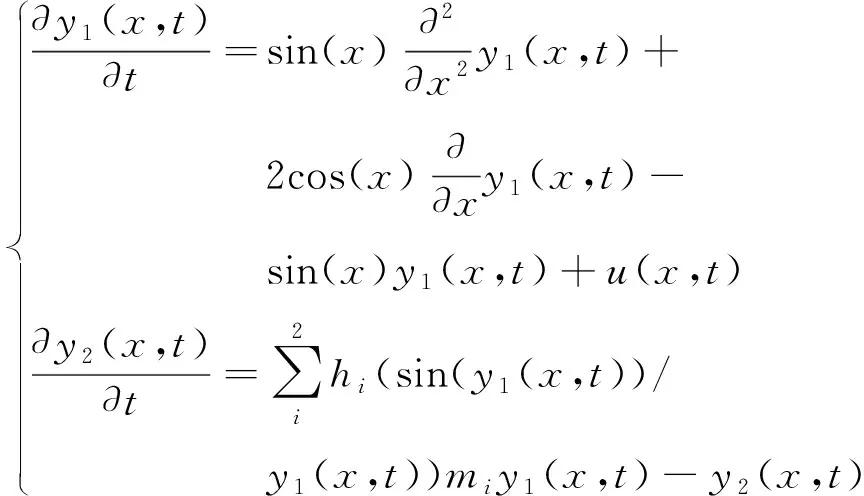
由此可以计算


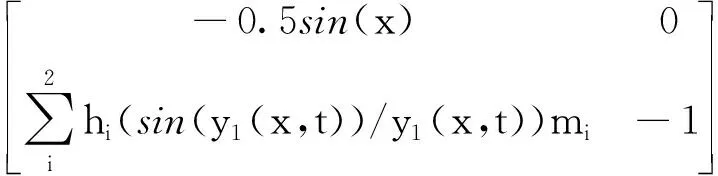
设置极点为-1±i,则
y1(x,t))mi)-1]
此时
令y1(x,t∞)=x/π,仿真结果如图2所示。
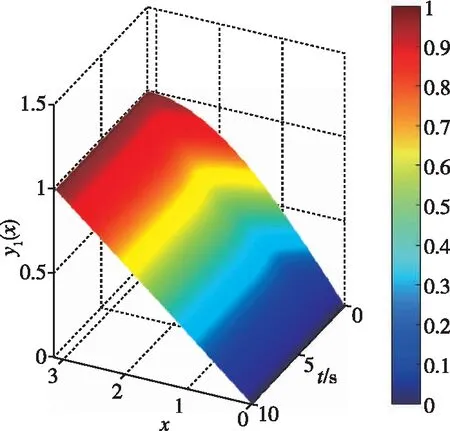
图2 y1(x,t)演化图形Fig.2 Evolution diagram of y1(x,t)
4.2 具有第二类边界条件非线性分布参数系统
根据此方法设计状态变量具有二类边界条件的分布参数系统
该系统模糊T-S模型为

根据式(10),该系统是不稳定的,无控制器时,y1(x,t)的变化如图3所示。为满足系统的稳定性,按步骤设计控制器为
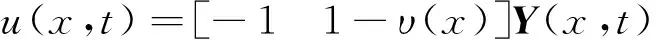
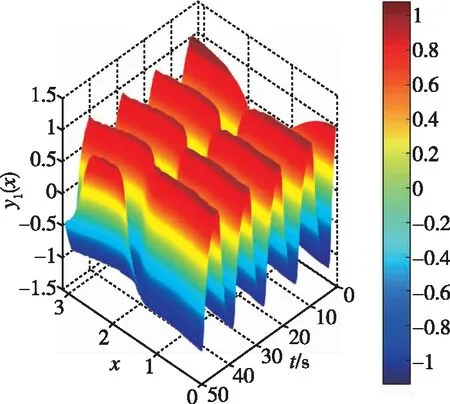
图3 无控制器y1(x,t)演化图形Fig.3 y1(x,t) evolution diagram without controller
引入控制器后,y1(x,t)的变化如图4所示。
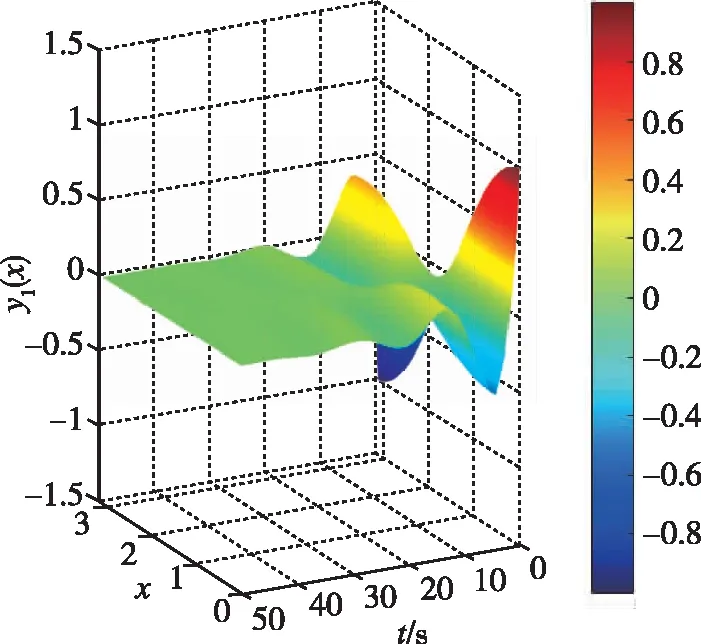
图4 引入控制器后y1(x,t)演化图形Fig.4 y1(x,t) evolution diagram with controller
4.3 非线性分布参数系统实例与方针
在核反应堆领域中,与反应堆功率相关的中子扩散方程如下
边界条件为z∈[0,1];t≥0;Nr(0,t)=0;Nr(1,t)=0。采用Lyapunov方法判断该系统的稳定性
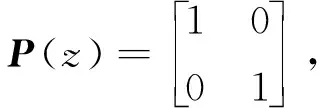
Nr(z,t))+f(Nr)ρr(z,t))+
Cr(z,t)(λ(Nr(z,t)-Cr(z,t)))+
ρr(z,t)(GVr(z,t))dt
经整理推导
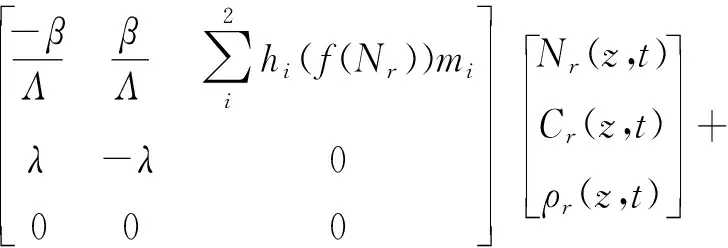
ρr(z,t)(GVr(z,t))dt
此时系统的稳定性是无法确定的,为保证系统稳定,设置期望极点为[-1+i-1-i-300],设计控制器为
Vr(z,t)=
令反应堆功率阶跃提高10%的仿真结果如图5和图6所示。
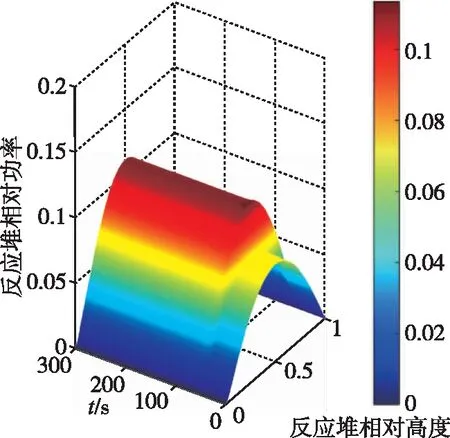
图5 加入极点配置后功率演化图形Fig.5 Relative power evolution after adding pole assignment

图6 未加入极点配置功率演化图形Fig.6 Relative power evolution without adding pole assignment
通过对比加入节点配置前后的反应堆相对功率演化图形可以看出,加入极点配置后的堆内相对功率分布响应快速,而未加入极点配置的堆内相对功率超调过大。
5 结论
分析Lyapunov函数时间微分项,并以此根据极点配置的方法设计状态反馈,其中对于极点配置无指导作用的部分有两项,分别为常数项以及分布参数系统中的非线性项。针对常数项的处理方法为引入状态变量的空间一次微分项进行抵消;针对分布参数系统中的非线性项采用T-S模糊模型进行表达。根据此思路设计的P-sD状态控制器应用于两个非线性分布参数系统数学模型的仿真结果可以得到如下结论:
1)P-sD状态控制器可以使分布参数系统稳定;
2)采用T-S模糊模型可以精确描述非线性分布参数系统。
此控制器设计方法就是基于Lyapunov稳定性推导而来,那么设计的控制器一定可以保证分布参数系统的稳定,对于非稳定的分布参数系统,该控制器表现出良好的性能。在仿真过程中,当隶属度函数如图1所示时,非线性模糊T-S模型与原非线性分布参数系统在任何状态都是相同的。因此,以非线性模糊T-S模型为参考设计的P-sD状态控制应用于原非线性分布参数系统不会带来模型化简所引起的偏差。

