采用双模压缩态的光子纠缠光纤陀螺仪研究

张桂才，冯 菁，马 林，马 骏，杨 晔,2，王周祥

(1. 天津航海仪器研究所，天津 300131；2. 中国船舶航海保障技术实验室，天津 300131)

0 引言

光纤陀螺是一种新型全固态光电惯性仪表，与传统的基于质量体动力学效应的机械陀螺相比，具有无运动部件、高可靠、长寿命、低成本、快速启动、动态范围大及精度覆盖面广等优点，已广泛应用于陆、海、空、天以及民用领域[1-2]。目前，国内外光纤陀螺技术的发展有两个方向[2]，一方面是基于传统干涉型光纤陀螺技术，面向高稳定、长航时及甚高精度的惯性测量和战略应用领域的产品研发和综合性能提升[3]，如法国iXblue公司已研制出实验室精度优于1n mile/30昼夜的潜艇应用光纤陀螺惯性导航系统[4]；另一方面是新的精度提升前沿技术的探索，如Honeywell公司提出了基于光子晶体光纤的用于绝对基准的紧凑型超稳定陀螺[5-6]。

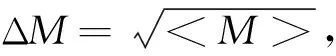
光子纠缠光纤陀螺仪由M. Fink在2019年首次提出，并获得了突破散粒噪声极限的实验结果[7]。在对光子纠缠光纤陀螺仪的研究中发现，如果采用传统光纤陀螺的单端口输入光学结构，即使采用非经典光子源，其相位检测灵敏度仍受散粒噪声限制，因此提出了采用双环行器的双输入/输出的光子纠缠光纤陀螺仪，并首次证明了这种双端口输入/输出结构仅对对称输入态才具备光路互易性。

双模压缩态是量子传感和测量中常见的一种对称非经典光量子态，其实验制备已有大量报道[10-12]，但其在光子纠缠光纤陀螺仪中的应用特性尚未被人们充分认识[13]。A. Kolkiran对采用双模压缩态的Sagnac干涉仪进行了理论探讨[14]，但给出的结果远未实现海森堡极限的相位检测精度。本文采用抽象自旋空间的角动量理论，首次对双模压缩态输入的光子纠缠光纤陀螺仪的相位检测灵敏度潜力进行了评估，并证明了当这种对称输入态的光子数足够大时，可以达到海森堡极限的相位检测精度，而进一步分析还揭示出，二阶符合计数的探测方案实际上存在量子增强相位信息的抵消，这正是A.Kolkiran的相关研究未达到海森堡极限相位检测性能的原因。本文对光子纠缠光纤陀螺仪的光源选型和探索新的相位检测方案具有参考意义。

1 双模压缩态及其特性

|in>=

(1)

可以看出，双模压缩态是一个对称输入的非经典态。

根据量子力学公式[17]

eξABe-ξA=

(2)

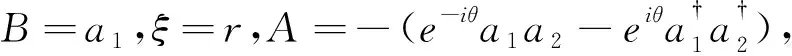
=a1

⋮

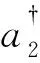
(3)

因而在海森堡图像中，真空态的双模压缩算符演变为

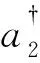
(4)

同理有

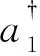
(5)

进而还可以证明

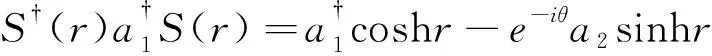
(6)

2 双模压缩态输入的Sagnac干涉仪和二阶符合计数

针对双模压缩态输入的量子Sagnac干涉仪需要双输入/双输出的光路特征，提出了一种采用双环行器的光子纠缠光纤陀螺结构，如图1所示。这种结构可以实现输入与输出的有效分离。在海森堡图像中，输入算符a1、a2经过理想Sagnac干涉仪在两个输出端口演变为输出算符b1、b2，且有[14]

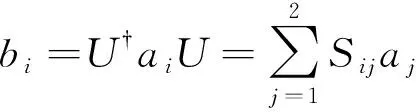
(7)

式中，Sij是Sagnac干涉仪的传输矩阵S的元素；U是与传输矩阵S对应的Sagnac干涉仪的演变算符。传输矩阵S与分束器、相移器(光纤线圈)有关，可以表示为

(8)

式中，φ为旋转引起的Sagnac相移

(9)

式中，L、D分别为Sagnac干涉仪的光纤长度和线圈直径；λ为输入光波的物理波长；c为真空中的光速；Ω为旋转角速率。

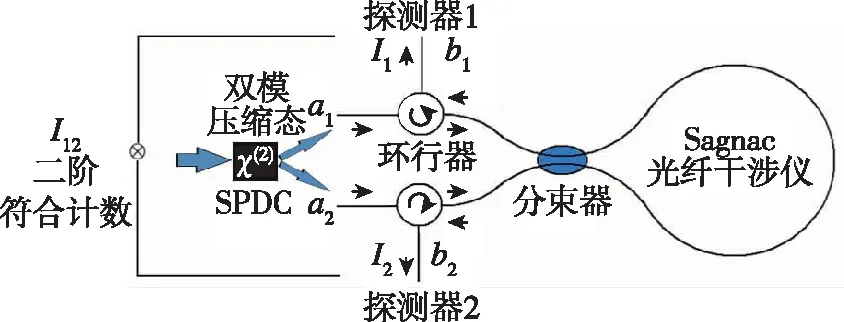
图1 双模压缩态输入的Sagnac干涉仪Fig.1 Sagnac interferometer with two-mode squeezed state input

同时，由式(7)和式(8)可以计算两个输出端口的输出光强I1、I2

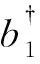
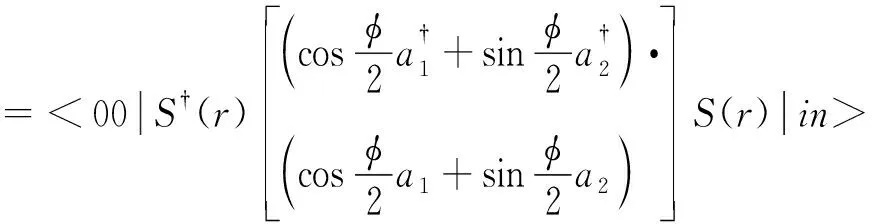
=sinh2r

(10)

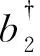
二阶符合计数I12计算为

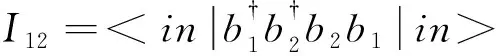
(11)

(12)

这是采用二阶符合计数探测方案的量子纠缠光纤陀螺仪的量子干涉公式。其中

(13)

也即被探测光子的纠缠特性导致一种缩短的德布罗意波长λD=λ/2，致使干涉条纹的频率增加2倍，相位响应也即Sagnac标度因数提高了2倍。

(14)

当2sinh2r>4时，Δφ甚至比Δφshot还大，不可能实现海森堡极限的相位检测性能，这也是在A. Kolkiran的文章中观察到的结果[14]。因此，需要进一步分析双模压缩态输入的光子纠缠光纤陀螺仪的相位检测灵敏度潜力。

3 采用角动量理论评估双模压缩态Sagnac干涉仪相位灵敏度

3.1 输入态的角动量表征

输入角动量Jx-in、Jy-in、Jz-in定义为[19]

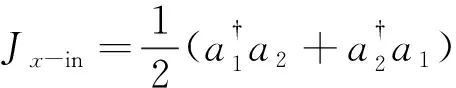
(15)

用输出湮灭算符b1、b2代替输入湮灭算符a1、a2，可以定义输出角动量Jx-out、Jy-out、Jz-out。

对于理想的Sagnac干涉仪，任何输入态|in>都是总光子数算符N的本征态|n1n2>

N|in>=(n1+n2)|n1n2>

(16)

总光子数算符N、角动量分量算符Jz(本征值为m)与角动量平方算符J2(本征值为j(j+1))对易，说明输入态是它们的共同本征态。角动量表征的输入态|j,m>与光子数态表征的输入态|n1n2>的关系有

(17)

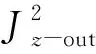
(18)

3.2 Sagnac干涉仪的角动量演变模型

实际上，任何一个双输入/双输出端口的无损耗无源线性量子光学器件都可以描述为在抽象自旋空间的旋转[21-22]。假定Sagnac干涉仪的分束器是分光比50∶50的理想分束器，对于Sagnac干涉仪来说，第一个分束器等效于使输入角动量绕x轴按逆时针旋转了角度π/2；相移器(光纤线圈)等效于使输入角动量绕z轴按顺时针旋转了角度φ；第二个分束器等效于使输入角动量绕x轴按顺时针旋转了角度π/2。图2作为一个简单例子，描述了抽象自旋空间中光子数态|n0>通过Sagnac干涉仪的演变。双模压缩态的输入角动量图示具有较复杂的形态，但通过Sagnac干涉仪的演变过程不变。

(a)输入态|n0>

Sagnac干涉仪的角动量矩阵变换可以表示为

(19)

可以看出，y向的角动量Jy不变，Sagnac干涉仪相当于一个绕y轴的角动量旋转变换。

3.3 双模压缩态输入的相位灵敏度潜力

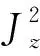
Jz-out=-sinφ·Jx-in+cosφ·Jz-in

(20)

得到

sinφcosφ·<00|S†(r)(Jx-inJz-in+

Jz-inJx-in)S(r)|00>

(21)

其中

<00|S†(r)(Jx-inJz-in+Jz-inJx-in)S(r)|00>=0

(22)

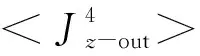
(23)

由输入角动量的定义，得到

sinh2rcosh6r+7sinh4rcosh4r+sinh6rcosh2r

(24)

=sinh2rcosh2r

(25)

式(23)中其他各项均为0。

由式(18)，在小角速率检测也即φ=0时，相位检测灵敏度(相位不确定性)有

(26)

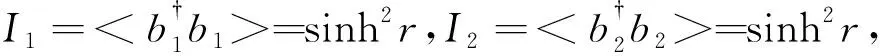
sinh2r=N/2

(27)

代入式(26)，因而有

(28)

4 二阶符合计数中的量子增强信息抵消

下面分析式(14)的二阶符合相位检测精度未达到海森堡极限的原因。由式(1)可以看出，双模压缩态是光子数态|nn>的叠加，其输出的形态非常复杂。这里以光子数态|22>为例,探讨双模压缩态输入的光子纠缠光纤陀螺仪的二阶符合计数中量子增强信息的抵消。对于光子数态|22>，经过Sagnac干涉仪后的输出态为

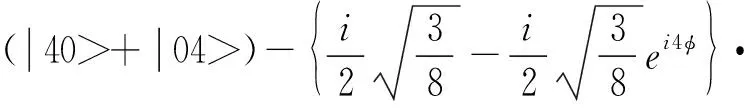
(29)

可以看出，干涉仪两个输出端口的输出态共有5个可能的光子数态：|40>、|04>、|31>、|13>、|22>，每个输出态具有各自的生成概率。|40>、|04>态的概率振幅中含有2φ和4φ相位信息，|31>、|13>中仅含4φ信息，|22>输出态也同时含有2φ和4φ相位信息。但是， |22>输入态的二阶符合计数(二阶相关光强)却不含4φ信息

(30)

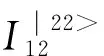
(31)

下标“12-o”表示其中一个探测器接收端光子数为奇数(odd)的光子数态|31>、|13>的二阶符合计数对4φ信息的贡献，式(31)已接近海森堡极限的相位灵敏度。

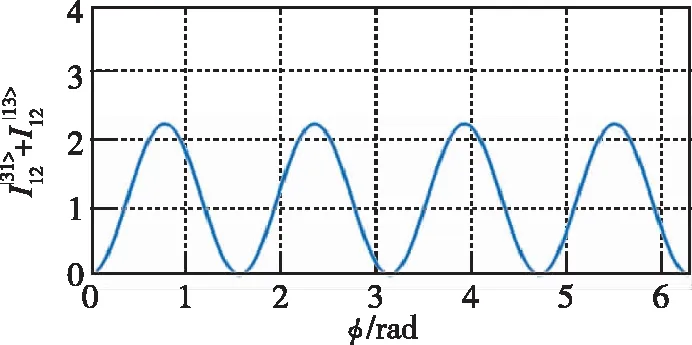
(a)其中一个输出端光子数为奇数的输出态的二阶符合计数

以上分析表明，在双模压缩态光子纠缠光纤陀螺中，采用二阶符合计数探测方案，实际上存在量子增强信息的抵消，导致相位检测灵敏度无法达到海森堡极限。因此，对于双模压缩态输入光子纠缠光纤陀螺仪，尽管其相位检测灵敏度潜力为海森堡极限，但探测方案应尽可能提取完整的量子增强信息，才能实现海森堡极限的相位检测灵敏度。

5 结论

本文对采用双模压缩态输入的光子纠缠光纤陀螺仪进行了研究：

1)针对双模压缩态输入的光子纠缠光纤陀螺仪的双输入/双输出特征，提出了一种采用双环行器的Sagnac干涉仪的光路结构，推导了二阶符合计数探测方案的量子干涉公式，发现二阶符合计数远未达到海森堡极限的相位检测性能。

2)采用四阶角动量理论首次分析了双模压缩态输入的光子纠缠光纤陀螺仪的相位检测灵敏度潜力，证明当光子数足够大时，可以实现海森堡极限。

3)针对双模压缩态光子纠缠光纤陀螺仪的二阶符合探测方案仅能实现超相位分辨率(干涉条纹加倍)而未能实现超相位灵敏度(达到海森堡极限)的情况，通过考察光子数态|22>经过Sagnac干涉仪后各个输出态分量的二阶符合计数特征，发现二阶符合计数探测方案存在量子增强信息的抵消，也即在其中一个探测器接收端光子数为偶数的输出态和光子数为奇数的输出态的二阶符合计数形成互补的倍频干涉条纹，进而相互抵消。

因此，本文认为，需要精心设计探测方案，提取完整的量子增强信息，才能在双模压缩态光子纠缠光纤陀螺仪中实现海森堡极限的相位检测精度。