岩块间软弱介质对块系岩体摆型波传播影响试验研究

王凯兴， 薛佳琪， 潘一山， 窦林名， 贾宝新

(1.辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000；2.中国矿业大学 深部煤炭资源开采教育部重点实验室，江苏 徐州 221116)

俄罗斯学者Sadovsky[1]提出岩体等级块系构造理论，认为岩体是由不同等级的具有软弱力学特性裂隙所分割的块体结构，并被地质力学领域研究不断证实。基于岩体等级块系构造理论，Kurlenya等[2-3]发现块系岩体中存在一种非线性动力传播现象并称之为摆型波，并从实测岩爆、化爆和块体模型施加脉冲载荷中分离出了摆型波波型曲线，如图1所示。图1中:tp和ts分别为纵波和横波到达时间；tμ为摆型波到达时间；t*为摆型波记录时间；Vp和Vs分别为纵波和横波波速，纵坐标为电压表示的位移幅值。

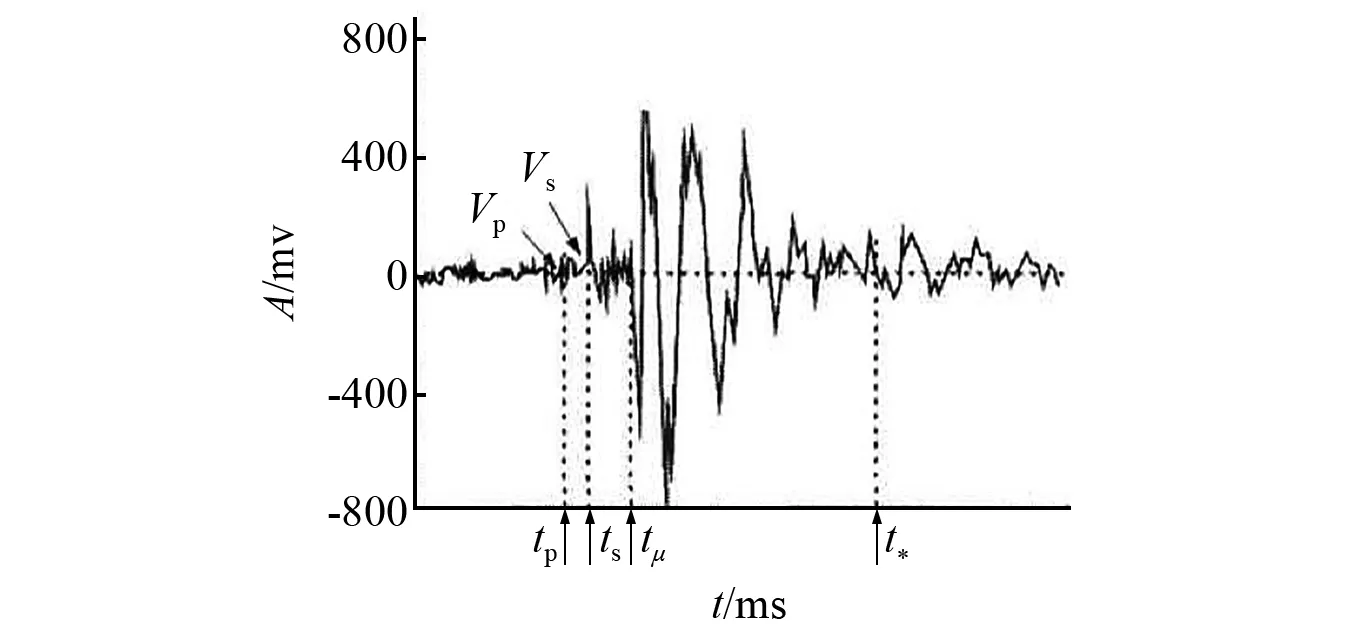
图1 地下爆炸时典型的位移波形Fig.1 Waveform of displacement on typical underground explosion

Aleksandrova等[4-6]从理论和试验上证实了摆型波在块系介质中的传播具有低频低速大摆幅运动的传播特性。Aleksandrova等[7-8]通过数值计算分析了摆型波波谱参数衰减率与夹层介质材料力学性质的相关性。Adushkin等[9-12]从岩体的块系构造出发讨论了摆型波的动力学特性，摆型波研究将为矿震及冲击地压现象提供预测手段。Oparin等[13]分析了地震诱发的摆型波对煤与瓦斯动力灾害的影响。Aleksandrova等[14-15]进一步分析了摆型波传播的二维及三维块状介质理论模型。我国学者也在这一领域做出了重要贡献，钱七虎[16]利用块系岩体中的摆型波波形曲线给出预报冲击地压动力灾害的3个临界参数。吴昊等[17]介绍了国内外摆型波现象的试验和理论研究进展，归纳出摆型波的主要特征参数及其变化规律。李杰等[18-19]研发了摆型波试验仪器及测量系统，通过试验揭示了冲击扰动作用下非线性摆型波产生的力学机理与传播规律。贾宝新等[20]采用理论分析与室内试验相结合的方法研究发现块体间介质黏性增加时，岩块加速度幅值有所下降。姜宽等[21-22]研究了夹层物理性质非均匀分布以及具有双模量特性的块系岩体对摆型波传播规律的影响。

岩块间软弱介质力学特性与摆型波传播密切相关，在块系岩体中岩块间弱介质最主要的特征就是岩体中软弱带的弹模和宽度变化，因此本文考虑块系岩体中岩块间软弱夹层的弹模及厚度对摆型波传播的影响。基于块系岩体动力传播试验，对比在不同弹模及不同厚度软弱介质作用下摆型波传播过程中的岩块时域和频域响应特征，得到岩块间软弱介质特性对块系岩体摆型波传播的影响规律，为岩体工程动力孕灾波动监测提供参考。

1 块系岩体摆型波传播试验模型

块系岩体摆型波传播试验主要由试验模型、冲击装置和测量装置三部分组成。试验模型由12个花岗岩立方块及岩块间软弱介质组成，岩块尺寸为100 mm×100 mm×100 mm，如图2(a)所示。为了分析块体间软弱夹层对摆型波的影响，本文分别采用两种夹层介质，其中夹层Ⅰ是弹模为2.2 MPa且厚度为1 mm的橡胶材料，夹层Ⅱ是弹模为0.37 MPa的泡沫材料且与夹层Ⅰ厚度相同，如图2(b)所示。冲击装置为质量0.3 kg的钢球从固定三角架上进行自由落体运动。测量装置采用TST-5915数据采集仪最高采样频率为100 kHz以及灵敏度为1 mV/g三向加速度传感器，测量范围±5 000g，频响5 kHz，三向加速度传感器分别粘贴在第3块(测点1)和第9块(测点2)岩块的侧面中心位置。

在一定冲击能量下岩块间的软弱夹层介质会发生较大变形，块体在其平衡位置形成较大幅度摆动，因此冲击能量水平和岩块间软弱夹层介质变形是摆型波产生和传播的关键因素。Kurlenya等[23]基于试验分析给出块系岩体摆型波传播的外在能量条件式(1)

(1)

式中：k为能量判据；参数θ和β满足条件1<θ<4；9<β<11；W为冲击能量；M为地质块体质量；Vp为纵波速度，在花岗岩中纵波的传播速度为Vp=5 400 m/s[24]。根据小球自由落体冲击和式(1)可得在200 mm冲击高度下k=1.84×10-9，满足块系岩体摆型波传播的外在能量条件。下面将分析小球在200 mm高度下冲击块系岩体，岩块间软弱介质弹模及厚度变化时摆型波传播的时域和频域响应特征。

图2 块系岩体动力传播试验模型Fig.2 Experimental model of dynamic propagation in block rock mass

2 块体间软弱介质弹模对摆型波传播影响

当岩块间分别含软弱夹层介质Ⅰ和软弱夹层介质Ⅱ时两测点在波动传播方向上的加速度响应曲线，如图3所示。

由图3可知，岩块间软弱介质弹模不同对块体加速度初始响应时间t、加速度响应值等均有影响。块系岩体在不同软弱夹层介质作用下的块体加速度响应及摆型波传播速度，如表1所示。表1中：amax为测点加速度最大值；ηamax为由测点1到测点2加速度最大值的衰减率。由图2的试验模型可知两测点间距为600 mm，则波速可由两测点初始响应时差计算得到，加速度信号时宽σt如式(2)。

(2)

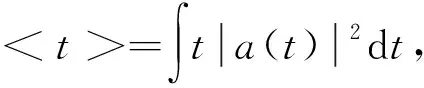
表1 不同夹层弹模下块系岩体摆型波传播特征Tab.1 Wave propagation characteristics of pendulum wave with different elastic modulus of weak medium

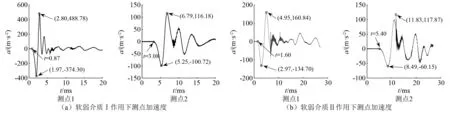
图3 岩块间软弱夹层介质弹模不同时块体加速度响应Fig.3 Block acceleration response with different elastic modulus of weak medium between the rocks

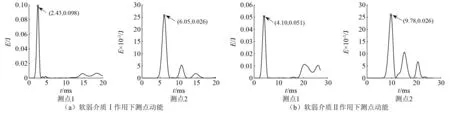
图4 岩块间软弱夹层介质弹模不同时块体动能响应Fig.4 Block kinetic energy response with different elastic modulus of weak medium between the rocks

块体动能响应特征量如表2所示。表2中：Emax为测点动能最大值；ηEmax为经过两测点动能最大值的衰减率；Δt1为两测点动能最大值出现的时差。

表2 块系岩体摆型波传播动能特征Tab.2 Kinetic energy characteristics in block rock mass of pendulum wave

由表2可知，块体间软弱夹层介质弹模增大时块体动能的最大值有所增加，但在传播过程其衰减更加明显。同时，两测点动能最大值出现的时差在缩短。岩块在冲击方向上产生的位移及回弹过程变化曲线可由速度曲线的数值积分得到，如图5所示。

由图5可知，在摆型波传播过程中，岩块位移沿冲击方向瞬间增大，而后逐渐恢复到平衡位置，表现为块体间软弱夹层介质的压缩和恢复过程，这是块系岩体摆型波动力传播的一个重要特征。比较图5(a)和5(b)可知测点1在软弱夹层Ⅰ作用下恢复到平衡位置所需时间更短，而测点2在软弱夹层Ⅱ作用下恢复到平衡位置所需时间更短，岩块位移响应特征如表3所示。表3中：xmax为位移响应最大值；ηxmax为在传播过程中位移最大值的衰减率。

由表3可知，随着岩块间软弱夹层介质弹模的增大，块体位移响应幅值下降，且在传播过程中位移响应幅值衰减明显。可见在摆型波传播过程中，块体间软弱介质弹模越小，块体的大位移摆动传播特性越明显。

表3 块系岩体摆型波传播位移特征Tab.3 Displacement characteristics in block rock mass of pendulum wave

在不同夹层介质作用下测点1和测点2加速度的频域响应，如图6所示。

图5 岩块间软弱夹层介质弹模不同时块体位移响应Fig.5 Block displacement response with different elastic modulus of weak medium between the rocks

图6 岩块间软弱夹层介质弹模不同时块体加速度频域响应Fig.6 Block acceleration response with different elastic modulus of weak medium between the rocks in frequency-domain

测点加速度信号的频域响应中心频率可表示为

(3)

(4)

它表示加速度信号主要持续于2σω的频带内。摆型波传播过程块系岩体的频域特征，如表4所示。

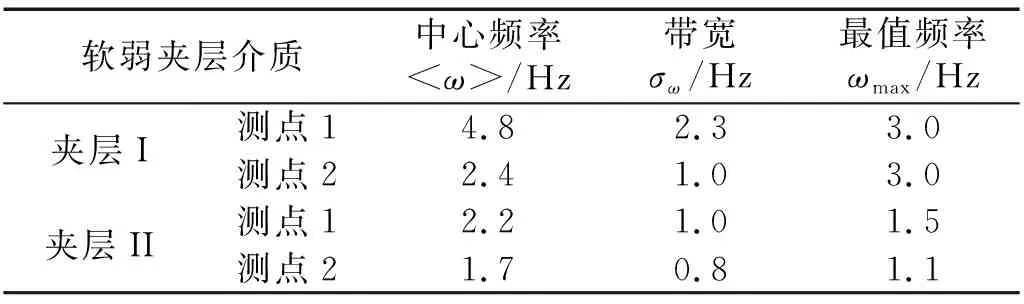
表4 摆型波传播过程测点加速度信号频域特征Tab.4 Signal analysis of rock acceleration in frequency-domain as the pendulum wave propagates

由表4可知，岩块间软弱夹层介质弹模下降时，两测点加速度带宽变窄，中心频率和最值频率也随之降低。表明软弱介质弹模下降后摆型波诱发块系岩体的低频响应愈加明显。

3 块体间软弱介质厚度对摆型波传播影响

下面分析在图2的试验模型和冲击条件下，改变块体间夹层厚度时摆型波的传播特征。块体间软弱介质采用夹层Ⅱ且夹层厚度为其2倍和3倍时，测点1和测点2的加速度响应，如图7所示。

块系岩体在不同厚度软弱夹层介质下的波动传播特征，如表5所示。

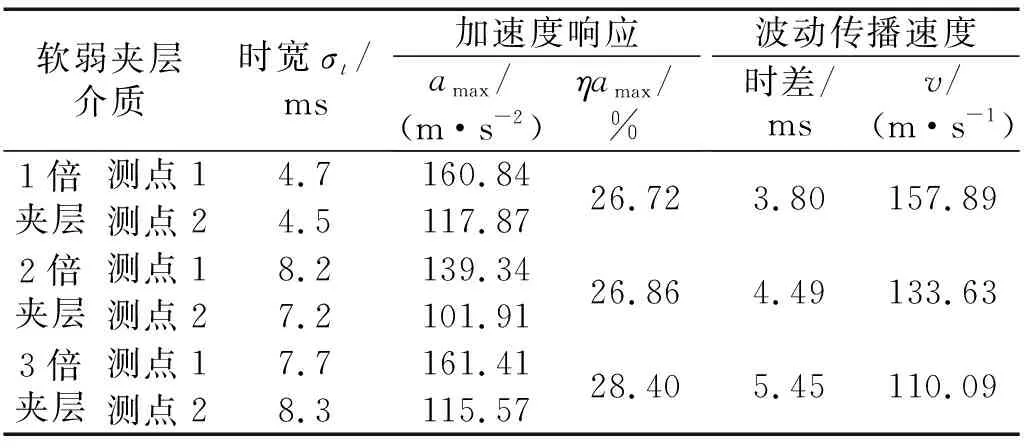
表5 不同夹层厚度下块系岩体摆型波传播特征Tab.5 Wave propagation characteristics of pendulum wave with different thickness of weak medium

由图7和表5可知，块体加速度幅值对夹层厚度变化没有明显的变化规律，但其传播过程加速度最大值的衰减随夹层厚度的增大呈增长趋势。同时，摆型波传播速度随块体间软弱夹层介质的增厚而逐渐下降，块体夹层增厚时加速度响应时宽总体呈现增大趋势。块体动能响应，如图8所示。

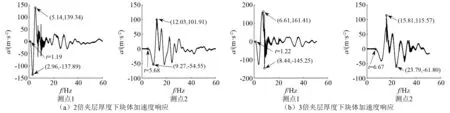
图7 岩块间弱介质夹层厚度不同时块体加速度响应Fig.7 Block acceleration response with different thickness of weak medium between the rocks

图8 岩块间弱介质夹层厚度不同时块体动能响应Fig.8 Block kinetic energy response with different thickness of weak medium between the rocks

结合图8得到块系岩体动能特征，如表6所示，其中Δt2为两测点动能最大值出现的时差。

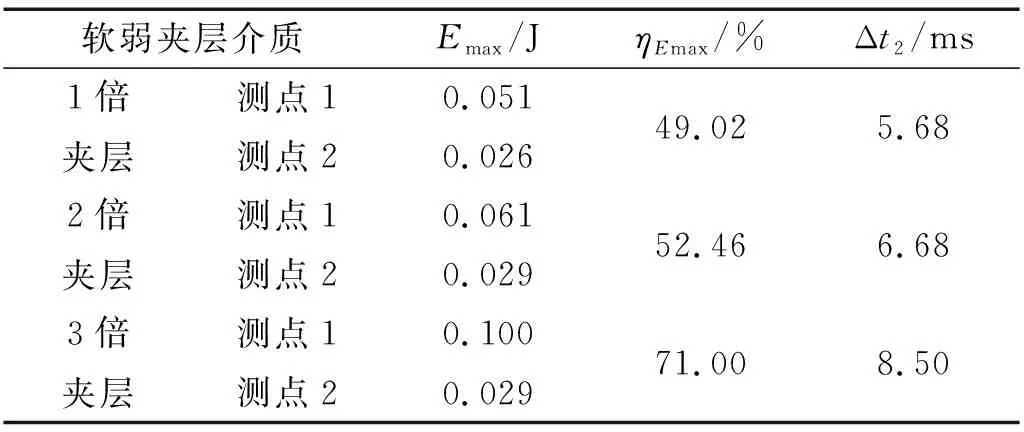
表6 块系岩体摆型波传播动能特征Tab.6 Kinetic energy characteristics in block rock mass of pendulum wave

由表6可知，随着块体间软弱夹层介质的增厚，岩块动能最大值变大，两测点动能最值出现的时差增大，波动传播过程块体动能的衰减率也明显增高。由速度响应积分得到测点块体的位移变化，如图9所示。

不同夹层厚度下块体位移响应特征，如表7所示。其中表7中的回跳时间是指块体位移由冲击方向上的最大值回复到平衡位置这一过程所经历的时间。

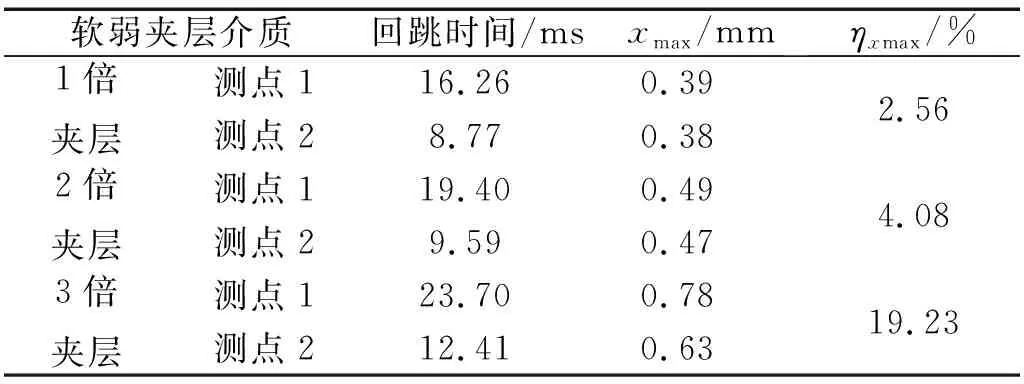
表7 块系岩体摆型波传播位移特征Tab.7 Displacement characteristics in block rock mass of pendulum wave

由表7可知，随着块体间夹层厚度的增加块体位移最大幅值显著增大，但其衰减率也明显增大。回跳时间的延长表明软弱夹层介质越厚岩块位移恢复到平衡位置所需的时间越长。块体加速度的频域响应，如图10所示。

结合图10，给出不同夹层厚度下摆型波传播过程测点加速度信号频域特征，如表8所示。

表8 摆型波传播过程测点加速度信号频域特征Tab.8 Signal analysis of rock acceleration in frequency-domain as the pendulum wave propagates

由表8可知，当岩块间夹层增厚时，测点的中心频率和带宽逐渐下降，但测点岩块最值频率受厚度的影响规律不明显。

图9 岩块间弱介质夹层厚度不同时块体位移响应Fig.9 Block displacement response with different thickness of weak medium between the rocks

图10 岩块间弱介质夹层厚度不同时块体加速度频域响应Fig.10 Block acceleration response with different thickness of weak medium between the rocks in frequency-domain

4 结 论

(1)软弱夹层介质弹模对摆型波传播影响：随着弱介质弹模的增大摆型波传播速度变快，岩块加速度和动能幅值变大、位移幅值变小，同时岩块加速度、动能及位移幅值的衰减率变大，加速度频响带宽增宽、中心频率及最值频率随之增高。

(2)软弱夹层介质厚度对摆型波传播影响：随着弱介质的增厚摆型波传播速度变慢，岩块动能和位移幅值变大、但对加速度幅值影响不明显，同时岩块动能和位移的幅值衰减率变大，加速度幅值衰减率有小幅增加，加速度频响的中心频率和带宽总体下降。

(3)由于当岩块间软弱介质的弹模下降或厚度增大时，块系岩体摆型波的低频低速大摆幅运动特征表现更为突出，因此在对围岩冲击灾害进行控制时，可通过固结破碎带增大其刚度及减小破碎带宽度，进而降低块系岩体摆型波传播带来的影响。