基于加权遗传算法的旋转机械不平衡振动溯源定位方法研究

康敬欣， 石瑞玉,2， 潘 鑫,2

(1.北京化工大学 机电工程学院，北京 100029;2. 北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室，北京 100029)

旋转机械存在多种故障形式，如转子不平衡、不对中、动静碰摩等。其中，转子不平衡是引发旋转机械故障的主要原因。由于加工工艺，加工误差等因素，可能导致转子质量分布不均的现象发生，进而在转子运行过程中引发故障。因此，针对旋转机械进行不平衡溯源定位及动平衡具有重大意义。

旋转机械基础动平衡方法主要有影响系数法、模态平衡法等。基于基础动平衡方法，诸多专家和学者提出了多种高效的、可行性强的平衡方法及相关算法。针对模态平衡法，黄金平等引入测点模态比的概念，提出利用起动过程中的瞬态幅度信息进行柔性转子双面平衡的新方法[1]。Li等[2]推导出一种针对高速柔性转子基于模态平衡法的方法。Khulief等[3]将实验模态分析，有限元建模和数学分析相结合，提出了一种综合实验与分析技术的现场动平衡方法。Zhao等[4]通过转子系统动力学方程的基本坐标变换和多模态分析，提出了一种新型瞬态平衡技术。在影响系数法的相关研究中，Untaroiu等[5]提出一种基于影响系数法的广义极小极大影响系数法，根据限制条件列出相关公式，转化为具有灵活目标函数和约束条件的优化问题，并编程计算。在实际平衡案例中，柔性转子动平衡占据了重要地位。章云等[6]通过提取不平衡量与振动响应之间映射关系，根据刚体力学理论，提出一种柔性主轴转子低速动平衡方法。岳聪等[7]利用升速响应信息进行柔性转子多阶、多平面瞬态动平衡方法研究。近年来，无试重平衡法因其不需要频繁启车的特性而受到瞩目。王维民等[8]提出一种基于数值模拟的无试重动平衡方法。宾光富等[9]构建了转子有限元模型，并进行不平衡响应分析，避免了通过频繁启车来确定影响系数。针对旋转机械的动平衡优化算法主要包括最小二乘法、遗传算法、粒子群算法等。Yao等[10]开展了遗传算法双重优化研究。唐云冰等[11]建立了多盘转子系统的计算模型，提出了运用优化算法对非线性系统进行等效线性化来平衡非线性支承转子的方法。徐宾刚等[12]研究了无试重起车情况下的动平衡理论及方法，利用遗传算法进行配重的优化搜索。邱海等[13-14]通过建立相关输入及输出的系统模型，利用遗传算法逆向求解出不平衡量。除此之外，还通过分析平衡过程的数学模型，提出了一种基于人工神经网络的转子动平衡方法。傅超等[15]提出基于转子加速起动瞬态响应，通过遗传算法识别不平衡量的方法对转子进行平衡。王星星等[16]将一种基于遗传交叉因子改进的粒子群算法引入到最小二乘影响系数法中。Zhong等[17]针对一种基于无监督深度学习的平衡方法进行了研究。

目前，已有诸多平衡方法均为综合考虑各转速各测点对应的振动状况，针对部分测点初始振动程度过高时的不平衡溯源问题尚未考虑。本文提出一种基于加权遗传算法的优化方法，该方法通过对各转速各测点对应的振动进行赋权，加强了不平衡溯源及动平衡的针对性及目的性，并分别通过有限元仿真与实验进行验证。

1 不平衡溯源定位基本原理

1.1 基于遗传算法的不平衡溯源定位

遗传算法是一类借鉴生物界的进化规律(适者生存，优胜劣汰)演化而来的随机优化搜索方法[18]，该算法被应用于诸多优化问题中。针对转子不平衡溯源定位问题，提出了一种基于遗传算法的转子不平衡溯源定位法。遗传算法基本流程，如图1所示。该方法根据转子试重前后的振动情况，结合遗传算法，对转子的初始不平衡量进行寻优，基本步骤如下：

步骤1测取各测点处在各转速下的振动情况。

步骤2依次在各加重面施加试重，得到各测点处试重后的振动情况。

步骤3根据试重前后振动情况，计算影响系数矩阵。

步骤4根据影响系数矩阵及残余振动方程组生成适应度函数，利用遗传算法搜索适应度函数的最大值。

步骤5输出最大适应度对应的转子初始不平衡量的解。

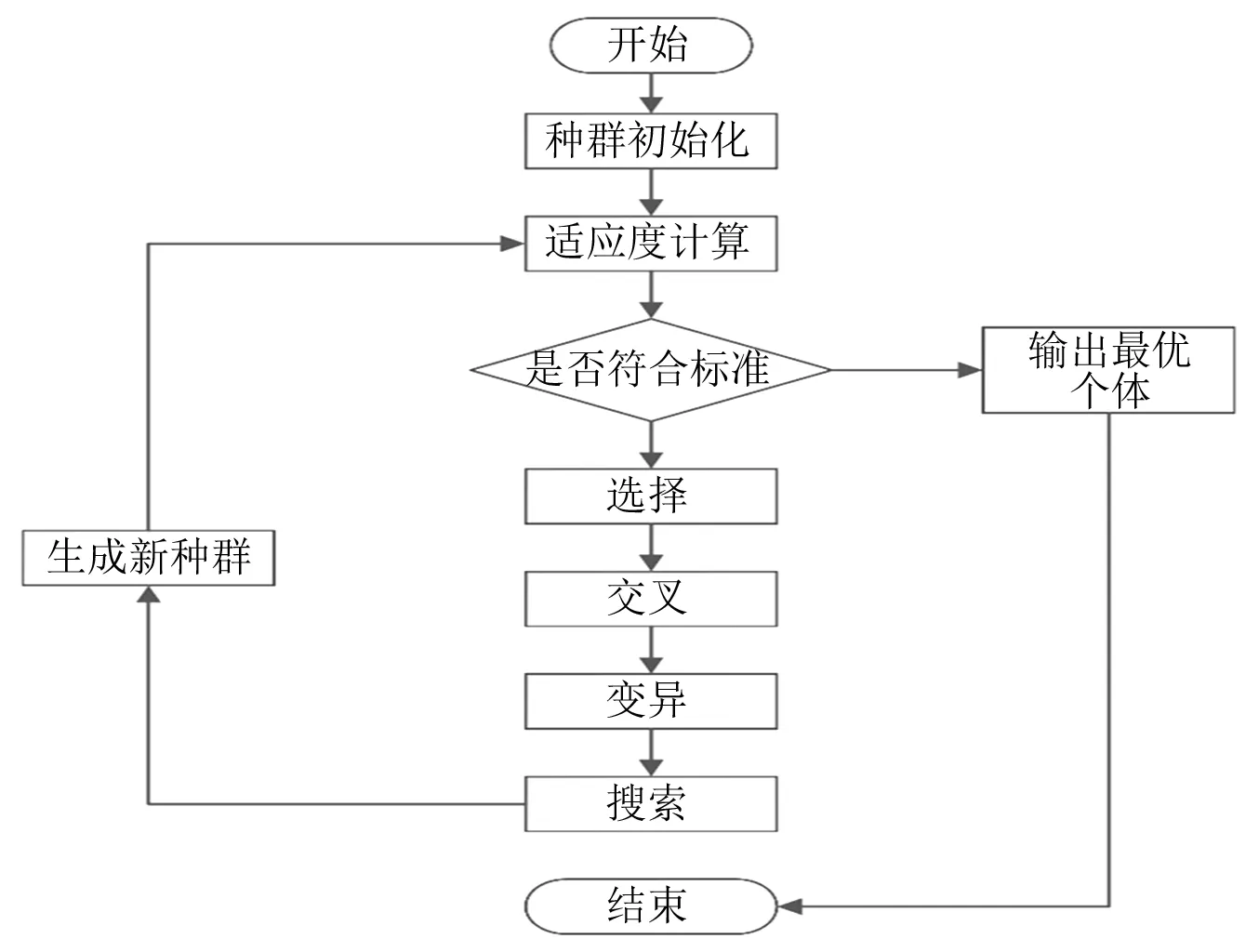
图1 遗传算法基本流程图Fig.1 Basic flow of genetic algorithm

遗传算法不平衡溯源中，主要参数包括种群规模、交叉概率、变异概率、迭代次数等。种群规模与遗传算法的效率相关，一般取20～100。交叉概率将对遗传算法中交叉操作的频率产生影响，一般取0.25～1.00。变异操作可使种群多样性得到保证，变异概率一般取0.001～0.100。迭代次数一般取100～1 000。

1.2 基于加权遗传算法的不平衡溯源定位

在利用遗传算法进行不平衡溯源定位时，通常可以得出一组综合各测点及各转速情况下的最优解，即最接近转子实际不平衡量的一组解，但各测点位置处对不平衡量的敏感程度可能存在差异，这种差异在影响系数矩阵中直接体现，进而对转子初始不平衡量溯源结果产生影响。在实际案例中，存在部分测点处初始振动远大于其余测点处初始振动的现象，为探寻导致该现象发生的原因，提升不平衡溯源定位的针对性，作者在原有的基于遗传算法的不平衡溯源定位法上进行改进，提出了一种基于加权遗传算法的不平衡溯源定位法。加权遗传算法基本流程，如图2所示。该方法主要对遗传算法中的搜索对象，即目标函数与适应度函数进行优化。为突出适应度函数中各组成部分对函数总体的影响，针对各测点各转速下振动平方值分别赋予权重，加权后的目标函数与适应度函数分别改进为

(1)

(2)

(3)

式中：f(x)为目标函数；F(x)为适应度函数；加权遗传算法是对适应度函数中的可行解进行寻优，得到使适应度函数值达到最大的解；Rxi，Ryi分别为x，y方向上各测点残余振动的第i个分量；Wi为各分量对应的权重；Cmax为一较大的常数，可根据实际案例取值。

在对各测点各转速下振动平方值加权时，依据各测点处初始振动幅值大小，对初始振幅较大的测点与工况适当提高权重，突出导致该现象的转子初始不平衡量。权重的选取依据初始振动情况，设初始振动较突出的测点与工况处平均振动水平为Vh，其余测点与工况下的平均振动水平为Vl，两种状况下的权重比为

(4)

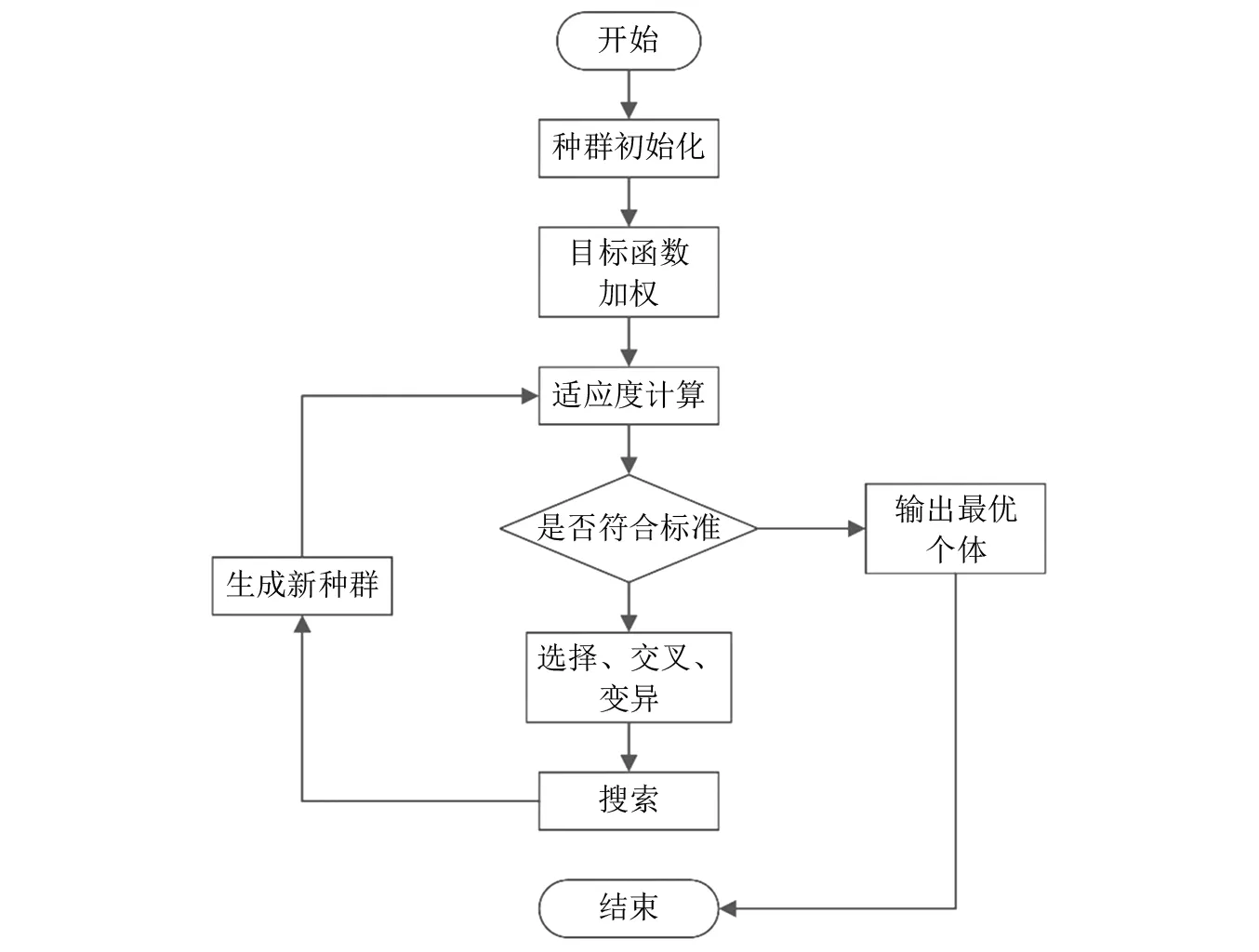
图2 加权遗传算法基本流程图Fig.2 Basic flow of weights genetic algorithm

2 轴系虚拟不平衡量溯源定位

2.1 双跨转子有限元建模及动力学分析

本文以某双跨转子实验台为例，根据转子相关参数，采用基于有限元技术的转子动力学分析软件DyRoBeS进行有限元建模。建模时对转子主轴、轴承、配重盘等进行模化处理，转子有限元模型，如图3所示。

图3 转子实验台有限元模型Fig.3 Finite element model of rotor

根据转子有限元模型可知，转子轴承分别位于节点2，6，8，12，配重盘分别位于节点3，5，9，11。各跨内两配重盘间的轴向距离均为180 mm。该转子各支撑处轴承均采用滑动轴承。

在各加重面位置处施加虚拟不平衡量，以模拟转子自身初始不平衡量及初始振动。四加重面模拟初始不平衡质量均为5 g，分别位于0°，90°，180°，270°处。依据构建的转子有限元模型，分析其临界转速及各阶振型，经过转子动力学分析，前4阶临界转速分别为3 038 r/min，3 172 r/min，6 963 r/min，7 220 r/min，各阶振型如图4所示。

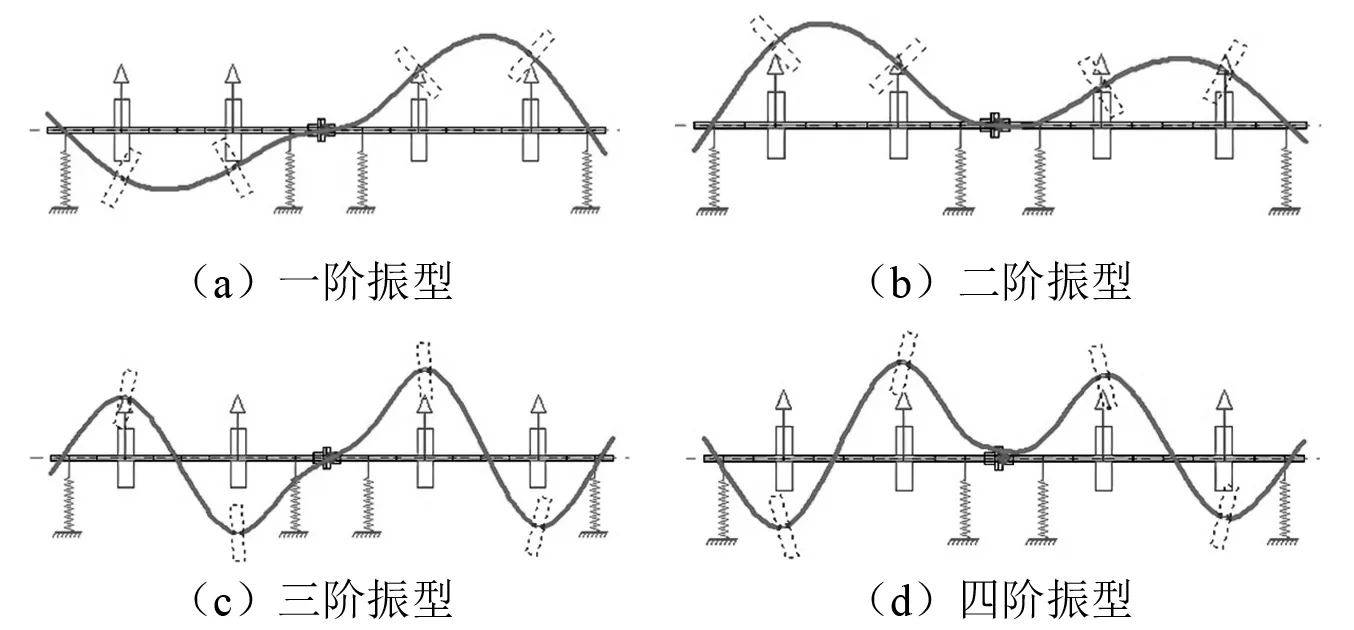
图4 双跨转子各阶振型Fig.4 Mode shape of shafting

由表1中各测点振动情况可知，节点6和节点8在3 500 r/min下的初始振动明显高于其余测点及转速下的初始振动。

表1 各测点初始振动Tab.1 Initial vibration of each measuring point 单位：μm/(°)

2.2 转子不平衡激励及响应分析

为进行转子不平衡响应分析，需在所构建的转子有限元模型基础上，在各加重面处再次施加虚拟不平衡以获得试重后各测点振动情况。依据2.1节中分析得出的转子临界转速，选择3 500 r/min，8 000 r/min作为该有限元模型不平衡溯源转速。在各加重面的0°位置分别施加虚拟不平衡量2 g，经过转子稳态响应分析，得到各测点各平衡转速下的振动情况，以此进行转子不平衡溯源定位。3 500 r/min，8 000 r/min时各测点试重后振动，如表2、表3所示。

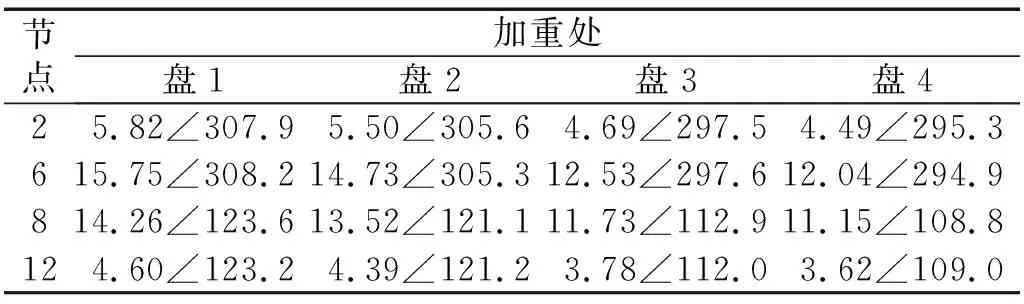
表2 3 500 r/min时各测点试重后振动Tab.2 Vibration of each measuring point after trial weights at 3 500 r/min 单位：μm/(°)

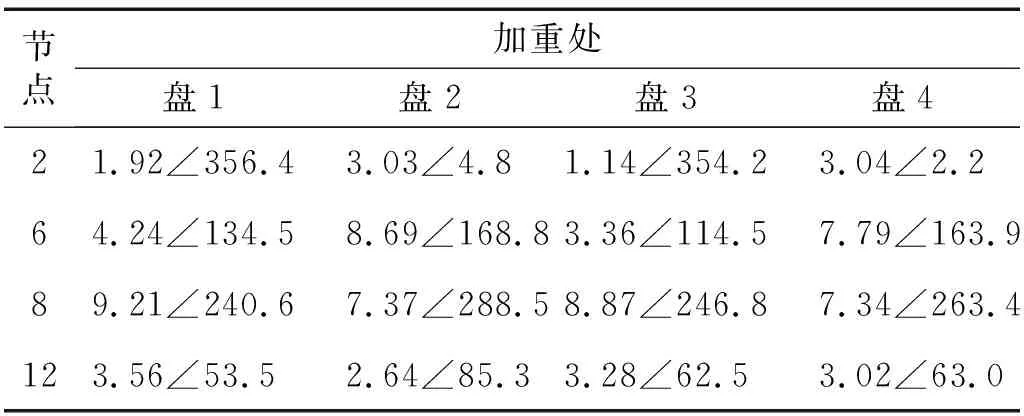
表3 8 000 r/min时各测点试重后振动Tab.3 Vibration of each measuring point after trial weights at 8 000 r/min 单位：μm/(°)

2.3 转子初始不平衡量溯源定位分析

根据各测点处的初始振动V0，以及各测点处试重后的振动情况Vk，可计算得出转子影响系数α及影响系数矩阵A，并进一步求得转子初始不平衡量。在求解转子初始不平衡量分布状况时，可通过多种算法进行求解，以选择更符合实际情况的一组解。

本文中，作者利用MATLAB软件中的 App Designer模块开发了一种转子不平衡溯源定位实用软件，该软件内置了3种不平衡溯源算法，分别基于最小二乘影响系数法(least squares method，LSM)、遗传算法(genetic algorithm，GA)、加权遗传算法(weight genetic algorithm，WGA)。

图5 不平衡溯源软件Fig.5 Software of unbalance traceability

利用3种算法分别进行不平衡溯源计算，加权遗传算法各测点各工况按1.3节中的规则赋权，为便于各权重计算并提升后续步骤的效率，节点6、节点8在3 500 r/min时赋予权重0.2，其余情况均为0.1。计算得出转子各加重位置初始不平衡量分布情况。

根据表4可知，3种算法的不平衡溯源误差均不超过5%，最大不平衡溯源误差分别为4.4%，3.4%，3.8%。综合各加重位置的不平衡量计算结果，基于GA的溯源精度略高于LSM。而WGA在部分加重位置处的溯源精度极佳，高于其余两种算法，如第二和第三配重盘处的溯源误差仅有0.4%和1.2%，低于LSM的3.0%，1.8%，以及GA的1.2%，3.4%。由此可见，基于加权遗传算法的不平衡溯源定位法在不平衡溯源中的较好的针对性。

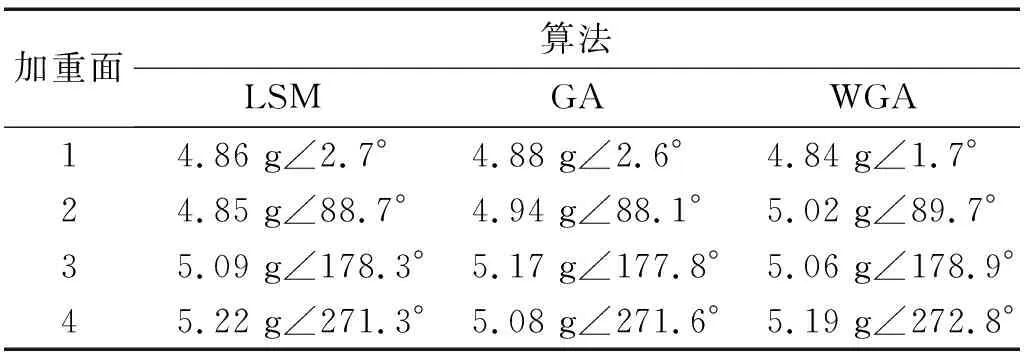
表4 不平衡溯源结果Tab.4 Results of unbalance traceability

3 转子不平衡溯源定位法实验验证

3.1 发电机转子实验台

为研究发电机转子在实际运行过程中的状态，搭建了模拟发电机转子实验台，如图6所示。该实验台的支撑部分为两个固定瓦轴承，由一台额定功率为55 kw的电机驱动，电机最高转速为3 000 r/min，转速可由变频器调节。实验台主轴上装有两个外径为600 mm的配重盘，该配重盘的加重半径为275 mm，两配重盘的间距为700 mm。转子悬臂端装有副励磁机。实验台测点布置如图6所示，共包含4个振动测点以及1个键相测点，所有测点均采用灵敏度系数为127 μm/V的电涡流传感器。4个振动测点均嵌于轴承盖中，分别命名为1x45，1x135，2x45及2x135。

图6 发电机转子实验台Fig.6 Test bench of generator rotor

3.2 发电机转子不平衡溯源分析

启动发电机转子实验台，根据转子实际工作情况，分别选择600 r/min,1 000 r/min,1 500 r/min作为本实验中的不平衡溯源转速，其中1 500 r/min为发电机实验台的工作转速。测得转子初始振动情况如表5所示。

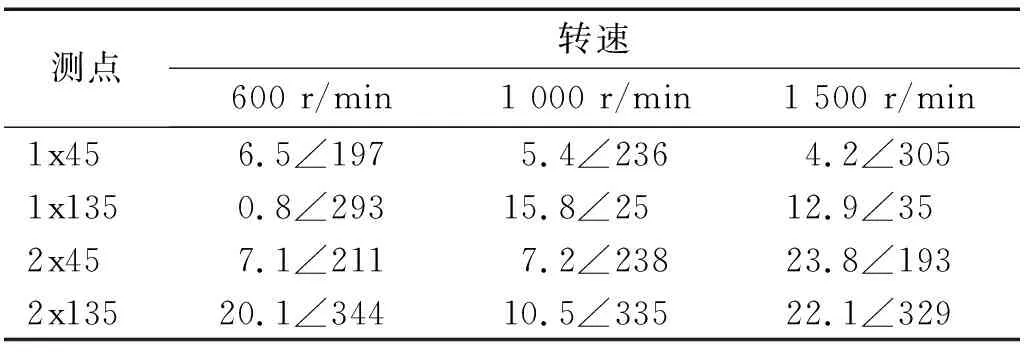
表5 各测点初始振动Tab.5 Initial vibration of each measuring point 单位：μm/(°)

由表5可知2x135测点、600 r/min；2x45测点、1 500 r/min以及2x135测点、1 500 r/min下的初始振动幅值较高，均超过20 μm，并作出2x45测点1 500 r/min初始振动情况，如图7所示。

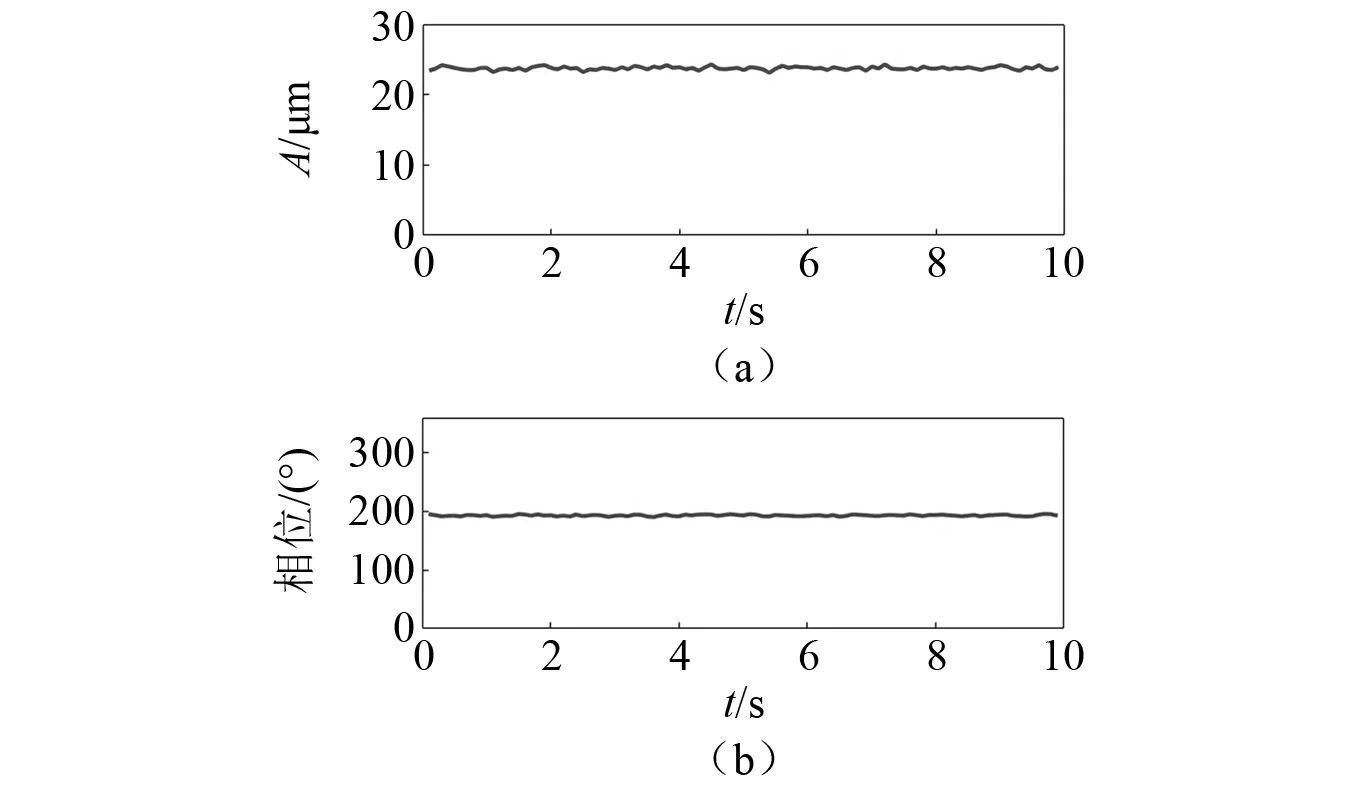
图7 2x45测点1 500 r/min初始振动情况Fig.7 Initial vibration at measuring point “2x45”,1 500 r/min

分别在配重盘1、配重盘2的0°位置施加112 g试重，进行转子不平衡响应测试，测得试重后各测点振动情况，如表6、表7所示。

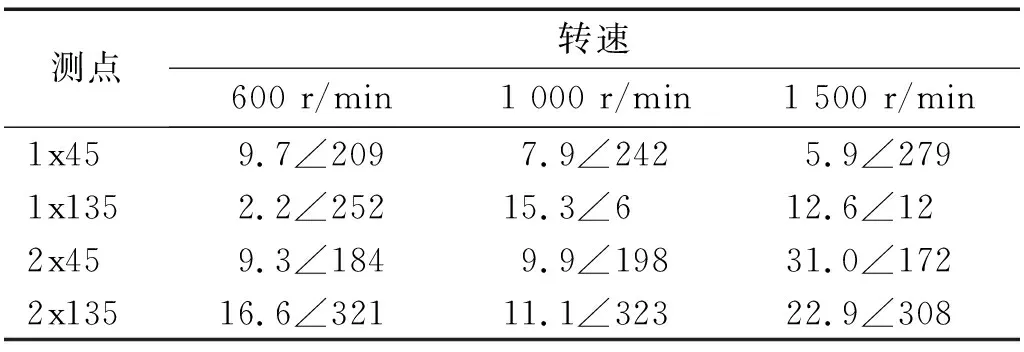
表6 配重盘1施加不平衡量后各测点振动情况Tab.6 Vibration of each measuring point after imbalance is applied to plate 1 单位：μm/(°)

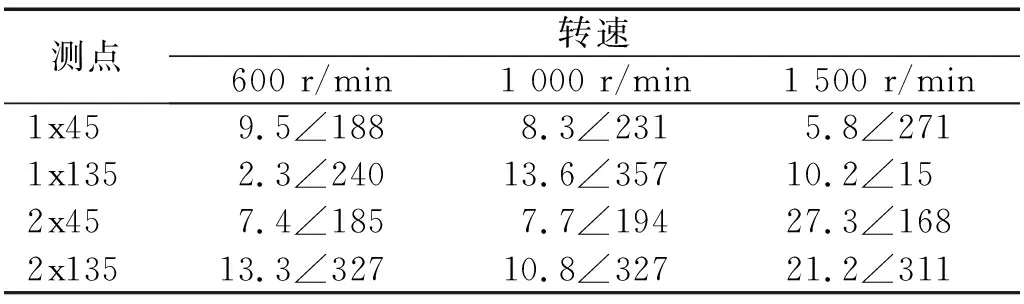
表7 配重盘2施加不平衡量后各测点振动情况Tab.7 Vibration of each measuring point after imbalance is applied to plate 2 单位：μm/(°)

对于该案例，测点数M为4，平衡转速数N为3，加重面数K为2，此时M×N>K，无法用一般的影响系数法进行初始不平衡量计算，故采用最小二乘影响系数法(LSM)、遗传算法(GA)、加权遗传算法(WGA)对转子初始不平衡量求解。通过转子不平衡溯源软件计算，得到转子初始不平衡量分布状况，各加重面的不平衡量分布如表8所示。

表8 配重方案Tab.8 Scheme of counterweight

为突出初始振动幅值较大测点处的不平衡量，通过基于加权遗传算法的不平衡溯源定位法计算转子不平衡量分布。对3个初始振动超过20 μm的工况点赋予权重0.133，其余工况点赋予权重0.067。

3.3 不平衡溯源定位效果验证

根据3.2节中溯源结果对各加重面进行配重，测得平衡后各测点处的残余振动情况，并与平衡前的初始振动进行对比，结果如表9所示。可再作出2x45测点1 500 r/min残余振动情况(WGA)，如图8所示。

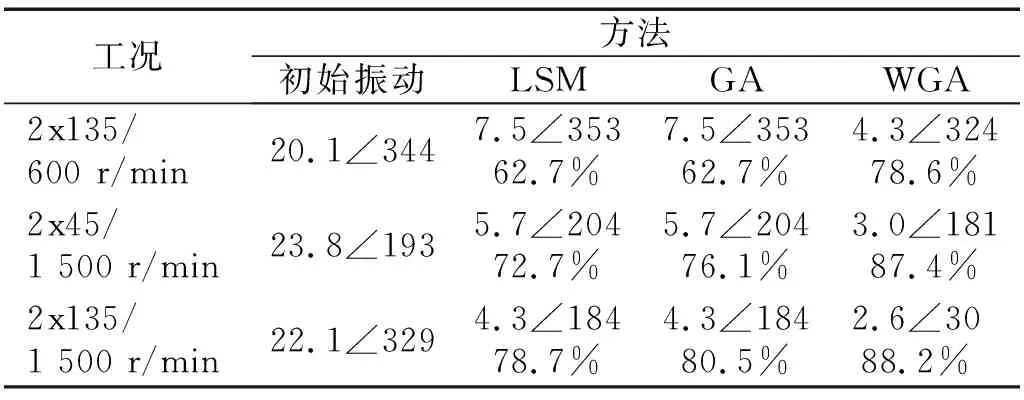
表9 各测点振动抑制效果对比Tab.9 Comparison of effect of vibration suppression at each measuring point 单位：μm/(°)

由该结果可知，LSM与GA的总体溯源精度相近，原因在于两种方法均综合考量所有测点与转速下的振动水平。本文所述基于WGA的不平衡溯源法在重点关注3个测点工况下的振动抑制效果均明显高于其余两种算法，如2x45测点/1 500 r/min及2x135测点/1 500 r/min时的振动降幅分别为87.4%，88.2%，优于LSM的72.7%，78.7%以及GA的76.1%，80.5%。由此可见，基于WGA的不平衡溯源法具有良好的目的性与针对性。

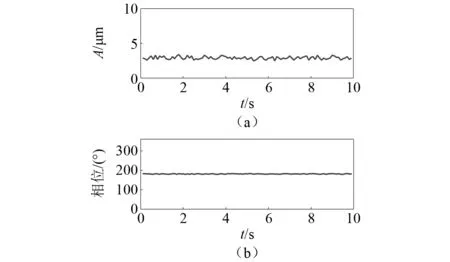
图8 2x45测点1 500 r/min残余振动情况(WGA)Fig.8 Residual vibration at measuring point “2x45”,1 500 r/min (WGA)

基于WGA算法的不平衡溯源结果进行配重后，实验台各测点的残余振动情况如表10和图9所示。

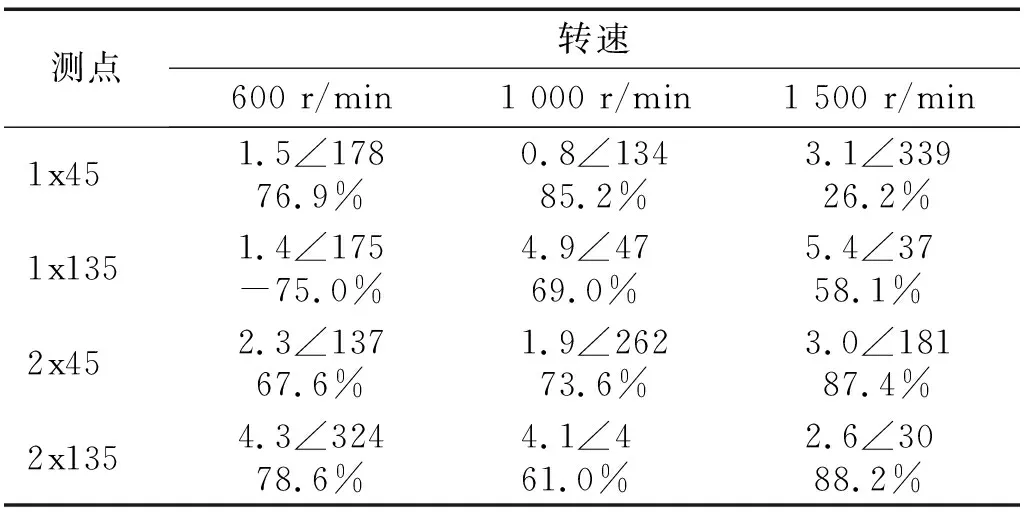
表10 各测点残余振动情况(WGA)Tab.10 Residual vibration of each measuring point(WGA) 单位：μm/(°)

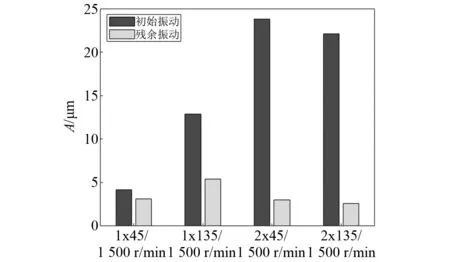
图9 基于WGA方法平衡前后振动结果对比(1 500 r/min)Fig.9 Vibration before balancing and after balancing based on WGA(1 500 r/min)

由上述结果可知，除个别初始振动已较低的测点外，基于加权遗传算法(WGA)进行转子系统的不平衡量溯源定位，均可有效抑制设备的不平衡振动，尤其对于初始振动较大的测点，该方法的平衡效果更加明显。

4 结 论

本文面向高端旋转机械多平面多转速下的不平衡振动溯源定位问题，提出一种基于加权遗传算法的转子不平衡溯源定位方法(WGA)，并通过仿真和实验将其与最小二乘法、常规遗传算法进行对比，验证其可行性。

在仿真分析中，WGA法针对多个配重盘的不平衡溯源精度均优于其余两种方法，其平均误差小于1%。在相关不平衡溯源实验中，根据WGA法溯源结果进行转子动平衡后，高权重测点处的振动抑制效果较其余两种方法更佳，振幅平均降幅超过80%。因此，综合仿真及实验结果，WGA法相较于改进前的方法，具有更好的针对性及更强的目的性。

在后续工作中，拟根据遗传算法基本原理，进一步开展针对该技术的优化工作，具体措施如设置多重目标函数及适应度函数，考量转子自身因素(转子支撑刚度、转子自身质量等)对该方法的影响，探究不同权重下各测点溯源效果等。