基于干扰观测器的含有柔性关节的柔性机械臂抑振策略
尚东阳, 李小彭, 尹 猛, 李凡杰, 周赛男
(1. 东北大学 机械工程与自动化学院,沈阳 110819;2. 中国科学院深圳先进技术研究院,广东 深圳 518055)
柔性机械臂广泛应用于太空探索、核电设备检修、工业装配等诸多方面。文献[1]所设计的“加拿大2号”机械臂是一种典型的柔性机械臂,它应用在国际空间站中。文献[2]提出了具有柔性双臂的新一代移动机器人平台。目前机械臂中多采用带有谐波减速器的一体化关节作为减速器。谐波减速器中存在着柔性部件以及弹性联轴器,所以一体化关节存在着一定的扭转刚度[3]。文献[4]将这种关节的扭转刚度加以考虑,提出了柔性关节的概念。含有柔性关节的柔性机械臂具有更轻的质量,更大的回转半径等优点。但是,柔性机械臂相比较于刚性机械臂,具有较小的抗弯刚度,在运动中更容易出现振动的现象。含有柔性关节的柔性机械臂的设计和抑振研究已经得到了许多学者的关注。
进行含有柔性关节的柔性机械臂控制研究的前提是建立受控对象的动力学模型。含有柔性关节的柔性机械臂是一个耦合的复杂非线性系统。文献[5]将含有柔性关节的传动系统等效为双惯量系统。据此,含有柔性关节的柔性机械臂也可以等效为含有柔性连杆的双惯量系统。根据文献[6],柔性机械臂通常可以等效成为欧拉-伯努利梁。文献[7-8]使用连续体振动理论描述柔性机械臂的变形,并应用拉格朗日原理建立其动力学方程。除了使用拉格朗日原理外,文献[9]使用哈密尔顿原理建立了柔性机械臂的动力学方程。随着计算能力的提高,利用有限元法获得柔性机械臂的动力学方程变成了可能[10]。在转动过程中,柔性机械臂还受到非线性摩擦力矩的影响。文献[11]在柔性关节的建模中,考虑了电机端摩擦力矩的影响。文献[12]使用LuGre模型描述机械臂在运动过程中所受的摩擦。但使用LuGre模型描述非线性的摩擦力矩时,会忽略温度、润滑等工况的影响。根据机械臂传动系统的结构可知,摩擦主要源于转动轴系和轴承之间的摩擦力矩。轴承摩擦力矩[13]将温度、轴向载荷、润滑等工况的因素考虑在内。
机械臂通常采用三环控制的策略(位置环速度环电流环)使转角获得稳定的输出。其中,机械臂的速度环多采用PI(proportional integral)控制策略[14]。随着控制理论的发展,鲁棒控制、自适应控制、神经网络控制等策略都应用于机械臂的控制。文献[15]使用鲁棒控制策略对柔性机械臂进行控制。文献[16]利用模糊规则整定PID(proportional integral derivative)控制参数,实现拟人机械臂的自适应控制策略。文献[17]利用神经网络辨识柔性机械臂动力学方程的不确定部分,由此提高控制精度。为了降低摩擦力矩对于机械臂的影响,干扰观测器(disturbance observer,DOB)广泛的应用于机械臂。文献[18]证明了干扰观测器能够有效的观测并补偿伺服系统中摩擦力矩。相比较于其他抗干扰控制策略,干扰观测器能够有效的辨识出外界干扰。干扰观测器的优势在于原理简单,需要设计的参数较少;缺点是不能有效地控制时变模型和强非线性的模型。对于一些时变系统,采用含有干扰观测器的PI控制策略无法获得良好的跟踪效果。因此,采用含有干扰观测器的PI控制策略适合于弱非线性且固定参数的动力学系统。
本文使用连续体的振动理论和拉格朗日方法建立含有柔性关节的柔性机械臂的动力学模型,并将轴承摩擦力矩予以考虑。通过李雅普诺夫稳定性定理设计含有干扰观测器的PI控制策略的超限补偿控制律。通过含有干扰观测器的PI控制策略抑制含有柔性关节的柔性机械臂的角速度波动。相比于文献[19]所建立的双柔性机械臂伺服系统的动力学模型,本文将轴承摩擦因素加以考虑。在含有干扰观测器的PI控制器的设计上,通过低通滤波器鲁棒稳定性的设计和引入超限补偿控制律保证柔性机械臂的稳定。
1 含有柔性关节的柔性机械臂动力学建模
本文所建立的考虑关节柔性的柔性机械臂由伺服电机、柔性关节、柔性连杆组成,如图1所示。图1中:XOY为静态坐标系;x0Oy0为动态坐标系;Ff为推力球轴承摩擦力矩;Tm为电机电磁力矩;Jm为电机端转动惯量;θm为电机端转角;θl为柔性连杆的转角;Ks为柔性关节扭转刚度;w(x,t)为柔性连杆的变形。

图1 双柔性机械臂伺服系统示意图Fig.1 Double flexible manipulator servo system
根据文献[20]可知,柔性连杆的变形可以认为是模态坐标和模态函数的二维函数,其表达式如式(1)所示。
(1)
式中:φi(x)为第i阶模态函数;ηi(t)为第i阶模态坐标;βi为模态函数特征根值,它与柔性连杆的固有频率之间的关系,如式(2)所示。
(2)
式中:ωi为柔性连杆的第i阶固有频率;ρ为柔性连杆的体密度;A为柔性连杆的横截面积;EI为柔性连杆的抗弯刚度。
柔性连杆在水平面转动的过程中,因为柔性的存在会产生微小的变形。因此,柔性连杆上任意一点在静态坐标系的位置如式(3)所示。
(3)
式中:x为柔性连杆上任意一点的横坐标;B(θl)为旋转变化矩阵。
根据式(3)可得到柔性连杆的动能,如式(4)所示。
(4)
同理,可得到柔性连杆的势能,如式(5)所示。
(5)
含有柔性关节的柔性机械臂除了由柔性连杆组成外,还有柔性关节和伺服电机。因此,含有柔性关节的柔性机械臂的动能应该由柔性连杆的动能和伺服电机的动能共同组成,如式(6)所示。
(6)
同理,含有柔性关节的柔性机械臂的势能应由柔性连杆的弹性势能和柔性关节的势能组成,其表达式如式(7)所示。
(7)
根据拉格朗日动力学方程,可求得含有柔性关节的柔性机械臂的动力学方程,如式(8)所示。
(8)
轴承在机械臂传动系统中起到支撑连杆转动的作用。但是轴承内圈转动的摩擦力矩会影响伺服系统的运动精度。根据文献[21]可得到轴承摩擦力矩的表达式,如式(9)所示。
Ff=M0+M1
(9)
式中:M0为与转速相关的摩擦力矩;M1为载荷相关的摩擦力矩。
M0的表达式,如式(10)所示。
(10)
式中:v为轴承润滑阻尼系数;n为转速;ωm为电机端的角速度;dm为轴承的平均直径。
M1的表达式,如式(11)所示。
(11)
式中:C0为轴承额定静载荷;p0为轴承的额定径向载荷;p1为等效载荷,它取决于载荷的大小和方向;Fa为轴向载荷,Fr为径向载荷。
含有柔性关节的柔性机械臂是一个复杂的非线性系统。为了方便设计干扰观测器,需要对动力学方程进行简化。根据Shang等和李小彭等的研究可知,转角和模态坐标耦合的非线性项对于系统的影响较弱。因此可以忽略非线性的影响。
简化后的含有柔性关节的柔性机械臂的动力学方程,如式(12)所示。
(12)
为了设计干扰观测器,需要获得受控对象的传递函数。在忽略动力学方程中的摩擦力矩后,对式(12)进行Laplace变换,可以得到式(13)。
(13)
在只考虑一阶模态的情况下,可以得到含有柔性关节的柔性机械臂的传递函数,如式(14)所示。
(14)
式中,Gn(s)为名义传递函数。
2 含有干扰观测器的PI控制策略
2.1 基于鲁棒稳定性的干扰观测器设计

低通滤波器的设计是干扰观测器设计的核心环节。低通滤波器应该同时满足鲁棒稳定性和抑制干扰的能力。
由于在获得名义传递函数的过程中,对含有柔性关节的柔性机械臂的动力学方程进行了一定的简化。除此之外,含有柔性关节的柔性机械臂在运动过程中,动力学模型的一些参数会发生改变。这种动力学模型的简化和参数摄动会造成名义模型和真实的伺服系统模型之间存在一定的误差。根据Yun等的研究可知,名义模型和真实模型之间的关系可以用乘积摄动描述,如式(15)所示。
Gp(s)=Gn(s)[1+Δ(s)]
(15)
式中: Δ(s)为摄动;Gp(s)为实际的传递函数。

图2 基于干扰观测器的角速度控制回路Fig.2 Speed control loop based on disturbance observe
根据Yun等的研究,可以得到整个闭环系统关于参数摄动的补灵敏度函数,如式(16)所示。
(16)
式中,TDOB(s)为干扰观测器内环的补灵敏度函数。
根据式(16),可得到TDOB(s)的表达式,如式(17)所示。
TDOB(s)=Q(s)
(17)
系统鲁棒稳定性的充分必要条件如式(18)所示。
‖Δ(jω)TDOB(jω)‖∞=‖Δ(jω)Q(jω)‖∞≤1
(18)
对式(18)进行变形,可得到式(19)。若低通滤波器的设计满足式(19),则可以保证系统稳定。
(19)
低通滤波器可以写成如式(20)所示的形式。
(20)
式中,α,β,χ为待设计参数。
通过调整系数,可以使低通滤波器满足式(20),保证系统获得稳定性。低通滤波器的伯德图,如图3所示。
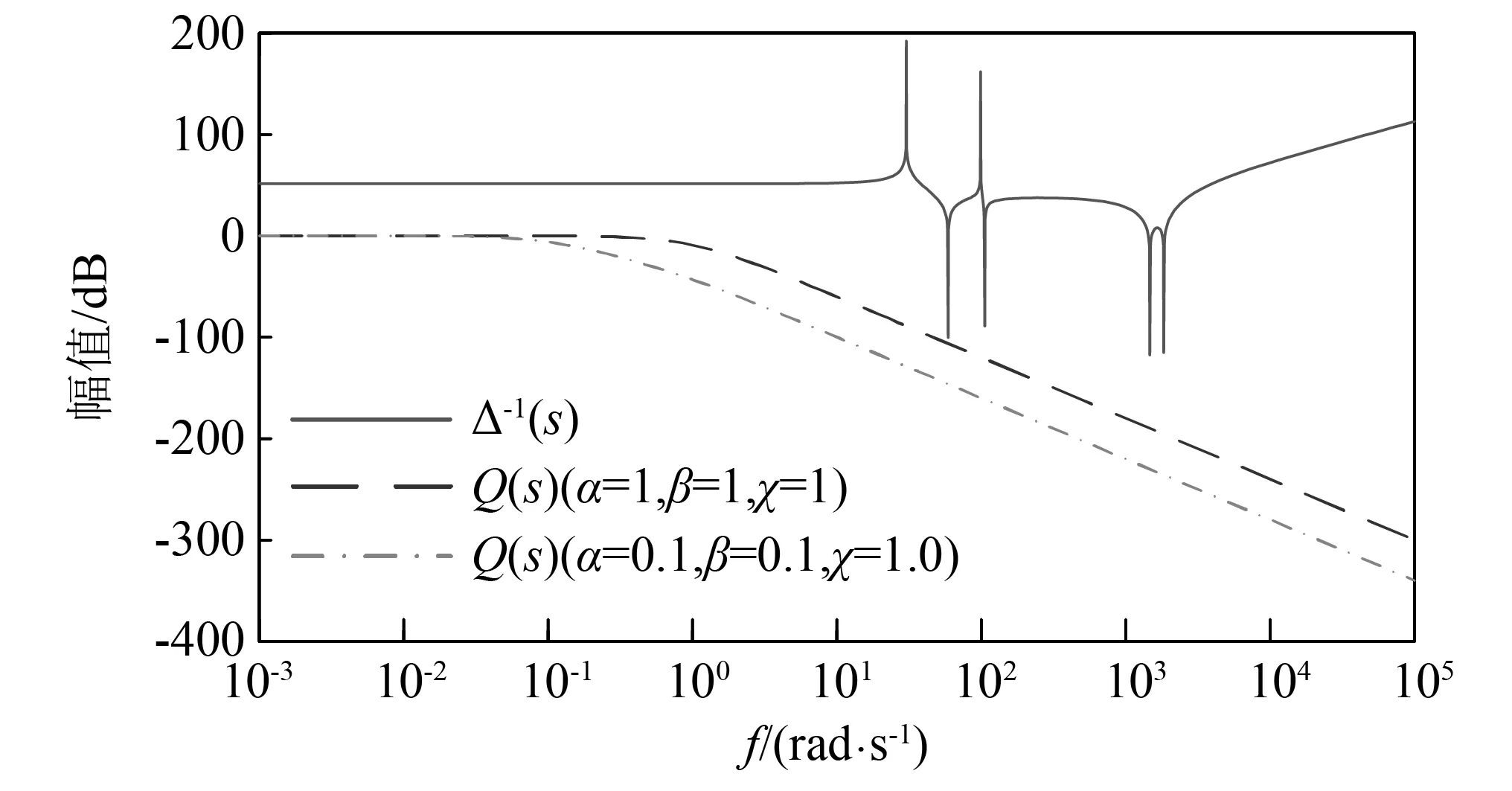
图3 低通滤波器伯德图Fig.3 Bode diagram of the low-pass filter
通过图3可知,低通滤波器的设计满足式(20),能够保证系统稳定。
2.2 超限补偿控制律的设计
在仅考虑一阶模态的情况下,根据式(15)可得到含有柔性关节的柔性机械臂的状态空间方程,如式(21)所示。
(21)
式中:ω为广义速度;u为双柔性机械臂伺服系统的输入力矩;d为由轴承摩擦力矩和其他未知因素所引起的干扰。
根据文献[22]可知,由于电流环和速度环之间的带宽较大,因此可以忽略电流环的影响。本文使用PI控制器对速度环进行控制。PI控制器的控制律,如式(22)所示。
(22)
式中:Kp为控制器比例参数;Ki为控制器积分参数;e为误差。
根据式(21),可得到式(23)。
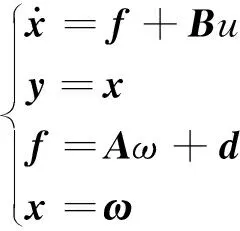
(23)
式中,f为伺服系统已知函数,它是一个有界函数,且具有上界。
根据式(23)可到标准的反馈控制率,如式(24)所示。
(24)
式中:ω*为期望速度矢量;E为误差向量;D矩阵表示一组正矢量参数,满足式(25)。
(25)
式中,k1和k2为正数向量。
本文所提出的控制策略的控制律由3个部分组成,如式(26)所示。
u=uPI+uDOB+uSC
(26)
式中,uSC为超限补偿控制律,它用来保证系统稳定。
式(26)中,干扰观测器的补偿控制律的表达式,如式(27)所示。
(27)
为了使本文所提出控制策略的控制律能够与标准的反馈控制律一致,应用李雅普诺夫函数设计PI控制器的超限补偿控制律。
将式(27)代入式(23),可得到式(28)。
(28)
根据式(28)可得到式(29)。
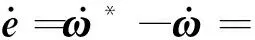
(29)
根据式(29)可得到式(30)。
(30)
定义李雅普诺夫函数如式(31)所示。
(31)
式中,P为正定对称矩阵满足式(32)。
(32)
式中,Q为给定的正定对称矩阵。
根据式(31)可得到式(33)。

(33)
根据式(33)可得到式(34)。
(34)
式中,fU为已知函数f的上界取值。
设计超限补偿控制律,如式(35)所示。

(35)
含有柔性关节的柔性机械臂的控制框图,如图4所示。

图4 双柔性机械臂伺服系统的控制框图Fig.4 Control block diagram of the double flexible manipulator servo system
3 数值仿真分析与控制实验
本文以含有柔性关节的柔性机械臂为研究对象,通过数值仿真分析和控制实验验证本文所提出控制方法对于抑制机械臂振动的有效性。为了验证这种机械臂的控制效果,本文在柔性机械臂处于两种不同长度的情况下开展仿真和控制实验,具体参数如表1所示。
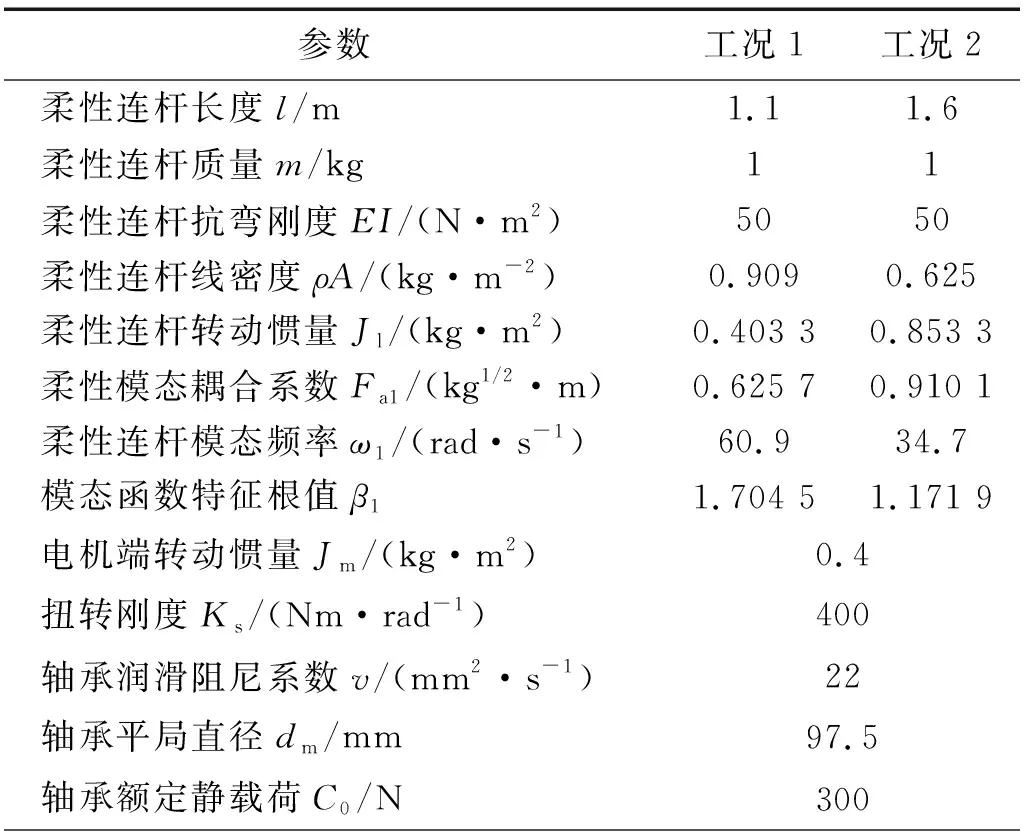
表1 含有柔性关节的柔性机械臂参数Tab.1 Parameters of the dual-flexible manipulator

表1 (续)
3.1 数值仿真实验
含有柔性关节的柔性机械臂在转动的过程中,受到摩擦力矩的影响。根据式(9)可知,轴承摩擦模型能够将温度、润滑、轴向载荷等因素加以考虑。相较于LuGre[23]模型和Stribeck模型,轴承摩擦模型能够更加准确地描述伺服系统中摩擦力矩和转速的函数关系。本文在数值仿真过程中以轴承摩擦力矩作为伺服系统所受到的外界干扰。为了验证伺服系统控制策略的跟踪效果,采用正弦函数作为伺服系统角速度的期望输入。以工况1的参数开展数值仿真分析,使用干扰观测器观测到的摩擦力矩和伺服系统的输入力矩,如图5所示。其中:图5(a)表示经过干扰观测器辨识的摩擦力矩;图5(b)表示系统的输入力矩。
根据图5(a)可知,经过干扰观测器辨识的摩擦力矩会出现微小的波动,这是由于名义模型和实际模型存在误差。但通过干扰观测器中低通滤波器的鲁棒稳定性设计可以保证伺服系统参数摄动的稳定性。由于静摩擦因素的影响,在角速度方向改变的瞬间,轴承摩擦力矩会发生突变。摩擦力矩的突变引起伺服系统所需控制力矩的突变。在真实的控制中,控制器无法在瞬时改变伺服系统的输入力矩。由此会引起伺服系统输出转速的波动。干扰观测器可以通过补偿摩擦力的方式削弱摩擦力矩突变对于伺服系统的影响。根据图5(b)可知,使用干扰观测器后,伺服系统所需的输入力矩的突变得到了明显的改善。
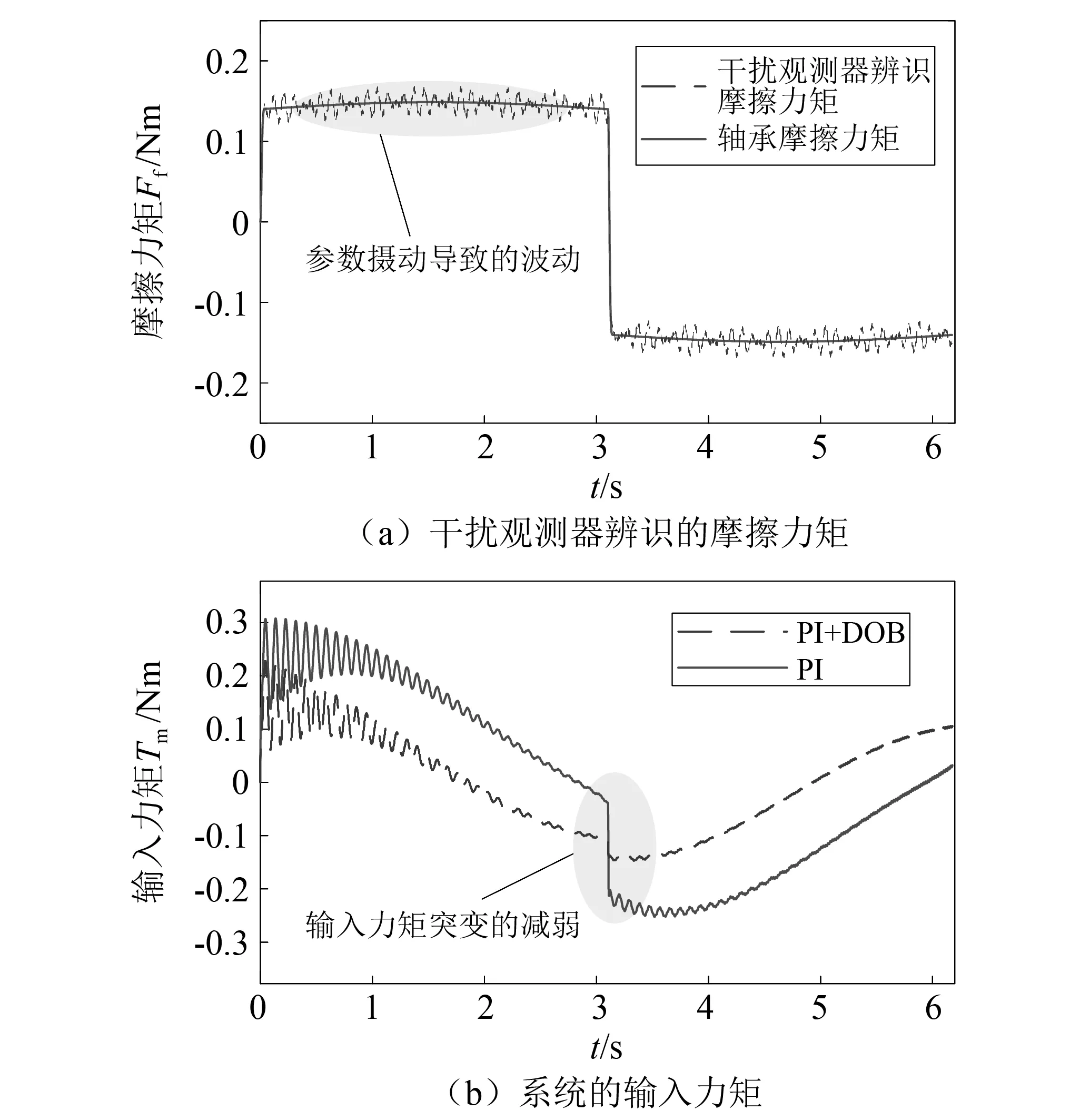
图5 摩擦力矩仿真结果Fig.5 SIMULINK results of friction torque
含有柔性关节的柔性机械臂末端执行器的振动除了与电机端的输出转速有关外,还和连杆端输出转速的波动有关。同样,根据工况1和工况2的参数开展数值仿真实验,得到不同控制策略下仿真输出结果,如图6所示。其中:图6(a)和图6(b)表示连杆端的输出转速;图6(c)和图6(d)表示柔性连杆末端的变形。

图6 仿真输出结果Fig.6 SIMULINK results of the servo system
随着机械臂长度的增大,连杆的柔性也逐渐增强。根据图6(a)和图6(b)可知,在机械臂长度较长的情况下,连杆端的速度波动明显增加。但是使用本文所提出的控制策略能有效的减弱连杆端角速度的波动。根据图6(c)和图6(d)可知,随着机械臂长度的增加,在转动过程中末端变形波动程度也增大。使用本文所提出的控制策略,能有减弱末端变形的波动。由此,验证了本文所提出的控制可以抑制含有柔性关节的柔性机械臂的振动。
3.2 控制实验
本文搭建了含有柔性关节的柔性机械臂的控制实验平台,如图7所示。控制实验平台由伺服电机、柔性关节、柔性连杆、NI控制器、磁编码器等组成。因为套索传动的关节具有一定的扭转刚度,因此将这种关节等效为柔性关节。NI控制器由NI-Crio-9053模块、NI-9264模块和NI-9401数据采集模块组成。NI控制器中NI-Crio-9053作为下位机将控制信号输入NI-9264模块。伺服电机的输出力矩由NI-9264模块产生对应的脉冲信号控制。NI-9401数据采集模块采集电机端和连杆端磁编码器所测量的数据。并将所采集到的数据实时传入控制程序。

图7 双柔性机械臂控制实验平台Fig.7 Control experiment for the double flexible manipulator
根据表1中的参数,设置机械臂的长度。使用上述两种不同的控制策略对含有柔性关节的柔性机械臂的角速度进行控制。以正弦信号作为输入信号,所得到的伺服系统连杆端的角速度和误差的变化规律,如图8所示。
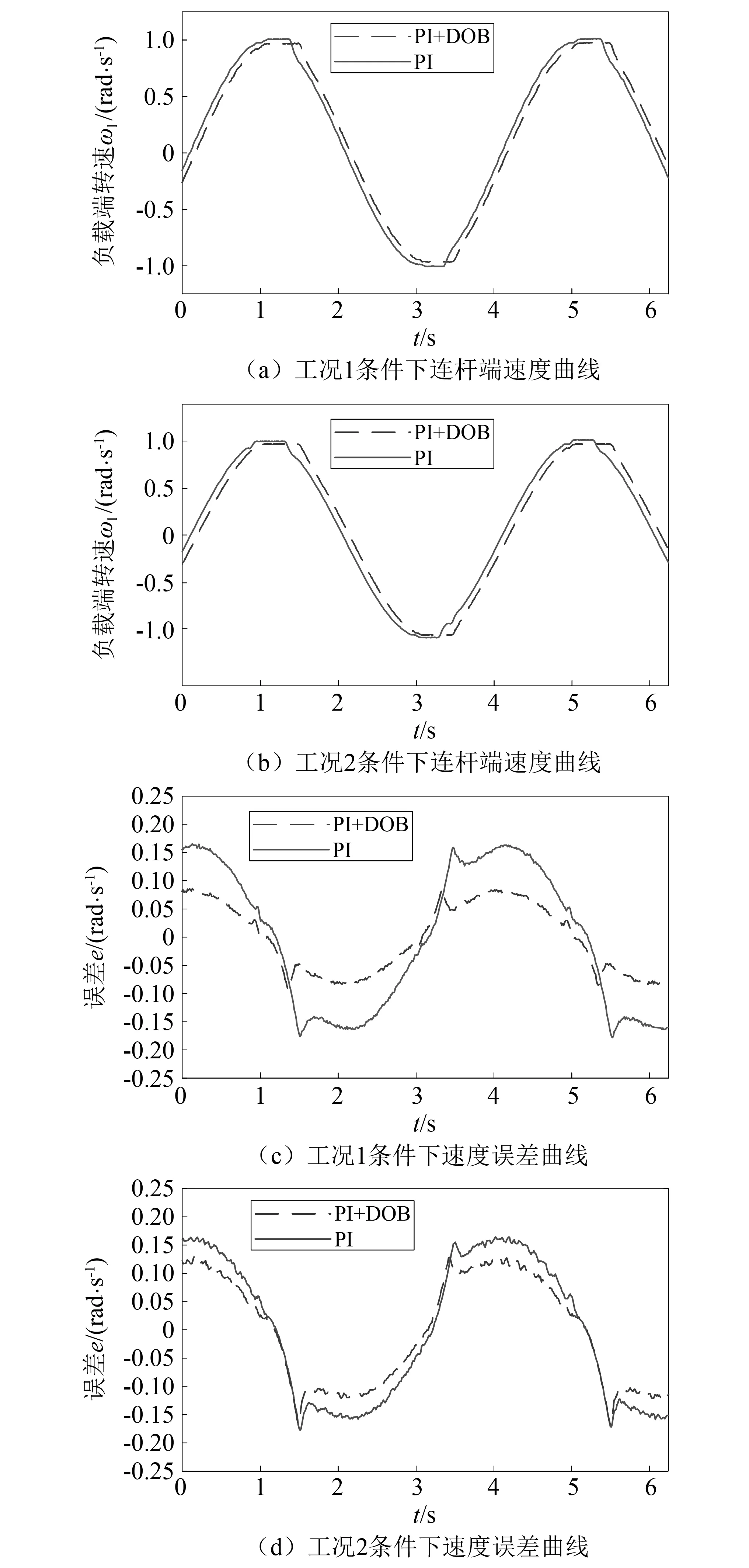
图8 实验结果Fig.8 Results of experiment control
根据图8(a)和图8(b)可知,随着机械臂长度的增加,使用PI控制控制策略已经无法保证伺服系统获得稳定的角速度输出。但是使用本文所提出的控制策略,仍然能够保证伺服系统获得稳定的角速度输出。根据图8(b)和图8(d)可知,使用干扰观测器能有效的减小角速度方向改变时产生的误差急剧增大的现象。因此,通过含有柔性关节的柔性机械臂的控制实验说明了本文所提出控制方法的有效性。
为了进一步评价控制策略的控制效果,本文对误差数据进行分析。以误差绝对值的平均值和误差的标准差作为评价指标。绘制了不同工况下的误差指标统计图,如图9所示。
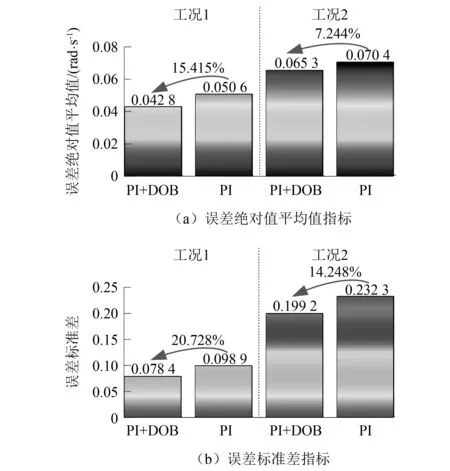
图9 误差指标统计图Fig.9 Statistical graphs of errors indicators
根据图9可知,无论在哪种工况下,本文所提出的控制策略都拥有更小的误差绝对值平均值和误差标准差。在机械臂较短的工况下,本文所提出的控制策略拥有更加明显的优势。在工况1情况下,相比于PI控制策略,本文所提出的控制策略能够使误差绝对值平均值降低15.415%;使误差标准差下降20.728%。在工况2情况下,本文所提出的控制策略能够使误差绝对值平均值降低7.244%;使误差标准差下降14.248%。根据统计数据可以证明本文所提出的控制策略能提高含有柔性关节的柔性机械臂角速度的控制精度。
4 结 论
本文以含有柔性关节的柔性机械臂为研究对象,使用拉格朗日方法建立了考虑轴承摩擦的动力学方程。然后应用含有干扰观测器的PI控制策略抑制伺服系统角速度的波动。在设计干扰观测器的过程中,考虑了参数摄动情况下的稳定性。使用李雅普诺夫稳定性定理设计控制器的超限补偿率。通过干扰观测器辨识并补偿伺服系统中的轴承摩擦力矩,以此减小摩擦力矩对输出角速度的影响。仿真结果和控制实验表明:本文所提出的控制方法能够抑制角速度的波动。具体研究结论如下所示。
(1) 在含有柔性关节的柔性机械臂中,当角速度的方向发生改变时,轴承摩擦力矩会发生突变。这种突变现象会加剧角速度的波动,进而增大误差。
(2) 干扰观测器可以有效的辨识出伺服系统中的摩擦力矩,并且干扰观测器通过补偿干扰力矩的方式,减弱摩擦力矩的影响。
(3) 根据仿真分析和控制实验可知,含有干扰观测器的PI控制策略更适合于机械臂较长的工况。本文所提出的控制策略在工况2的情况下,使转速误差绝对值的平均值下降11.33%;使误差标准差下降17.488%。由此可知,本文所提出的控制策略能够抑制含有柔性关节的柔性机械臂的角速度波动,进而减弱机械臂的振动。
干扰观测器的使用前提是受控对象能够用传递函数表示。多柔性连杆的机械臂是一个强非线性的复杂模型,无法获得它的传递函数。基于干扰观测器的控制策略不适用于多柔性连杆的机械臂。但是非线性的干扰观测器和其他抗干扰的控制策略可以用于控制多柔性连杆的机械臂。关于多柔性连杆的机械臂的建模和控制策略还需要进行深入的研究。在未来,希望能够将智能控制策略用于多柔性连杆机械臂的控制,以此解决强非线性模型的控制问题。

