数学里的绘画大师——函数

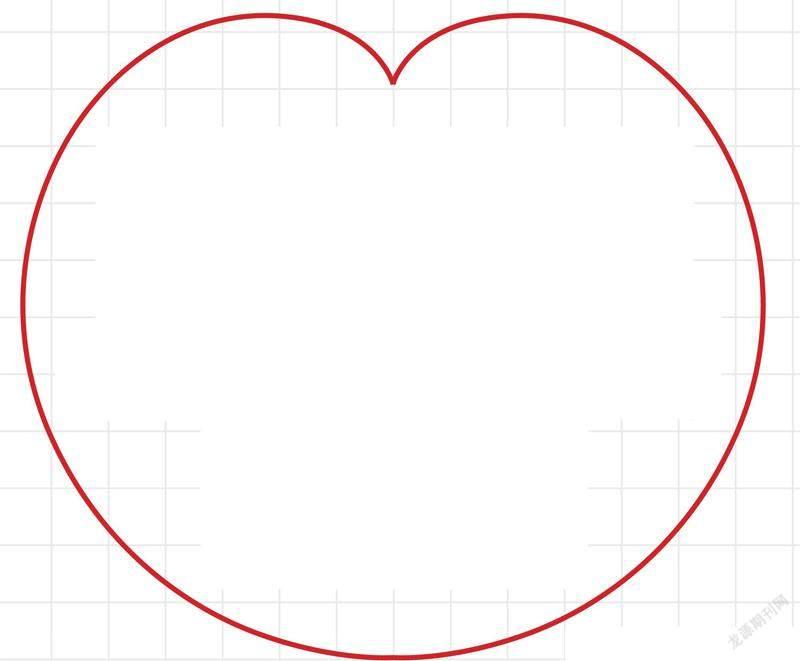
心形线（供图/ 张浩）

函数的由来

函数作为数学术语是德国数学家莱布尼茨在17世纪首次使用的，是指在某一变化过程中，两个变量x、y，对于某一范围内的x 的每一个值，y都有确定的值和它对应，y就是x的函数。例如：一次函数——y=kx+b（k，b是常数，k≠ 0）； 二次函数——y=ax²+bx+c（a，b，c是常数，≠0）。除此以外，数学中还存在很多隐含定义的函数，它们可以写成F（x，y）=0的形式，即无法明显地用一个变量的代数式表示另一个变量，但能确定y 是x 的函数，这些函数被称为隐函数。它们通常都有与之对应的曲线。

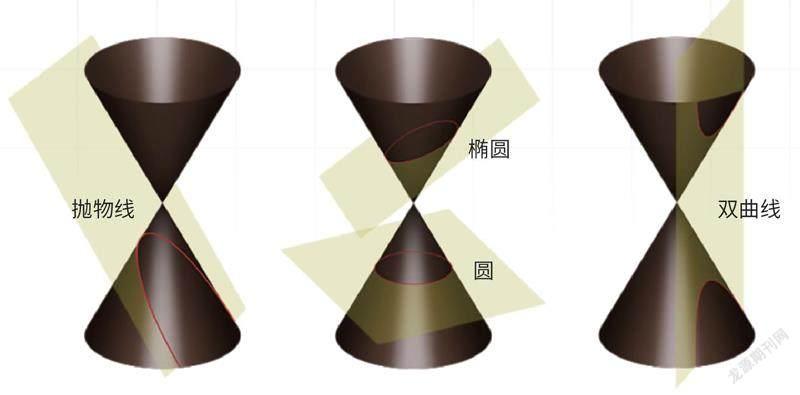
圆锥与圆锥曲线

生活里的函数图像

生活中的许多事物都有与之对应的函数。例如，我们购物时总价与数量间的关系，就是数学中最基本的一次函数；还有笔直的马路、竖立的旗杆的走向，都可以用一次函数来表示。炙热的太阳的轮廓是圆形，投篮时篮球的轨迹是抛物线，行星运行的轨道近似椭圆，发电厂冷却塔的外观近似双曲线，它们都可以用二次隐函数来表达，也被称为圆锥曲线。

顾名思义，圆锥曲线与圆锥有关。如果用平面去截一个圆锥，所截得的曲线可能是圆、椭圆、双曲线或者抛物线，这些就统称为圆锥曲线。在公元前3—4世纪，古希腊的数学家们就研究过这类曲线，其中的阿波罗尼奥斯是研究圆锥曲线的集大成者。

那些圆润柔美的函数曲线

茉莉花瓣曲线

笛卡儿虽然没有写下心形线，但他发现了另一条美丽的曲线——叶形线。1638年，笛卡儿首次得到叶子形状的曲线为x³+y³-3xay=0，有数学家认为这条美丽的曲线很像茉莉花瓣的样子，所以也被称为茉莉花瓣曲线。

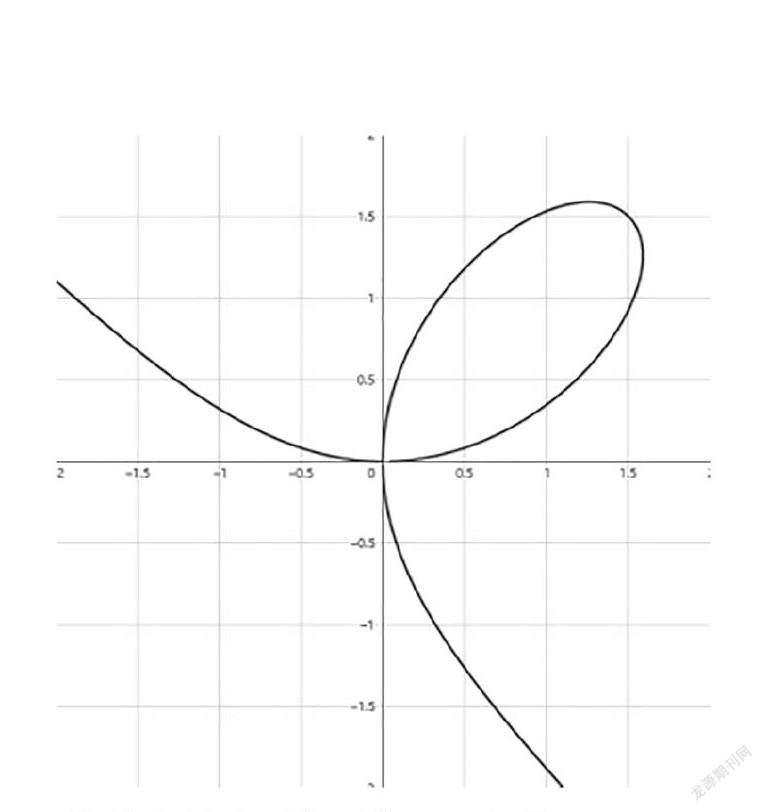
笛卡儿叶形线（供图/ 张浩）

玫瑰曲线

数学中还有著名的玫瑰曲线，它对应的函数为ρ=cos（kθ），当取不同的值时，可以得到不同花瓣、不同形状的玫瑰曲线。

对数螺线

笛卡儿还给出了对数螺线ρ=ae^kθ，因为这条曲线上任意一点和中心的连线与曲线上这点的切线所形成的角是一个定角，所以也被称为等角曲线。鹦鹉螺的外壳、蜘蛛网的形状就呈现出对数螺线形。

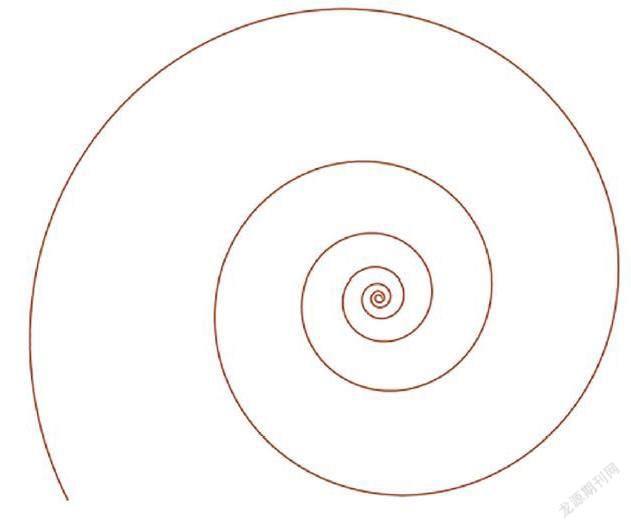
对数螺线（供图/ 张浩）

鸚鹉螺

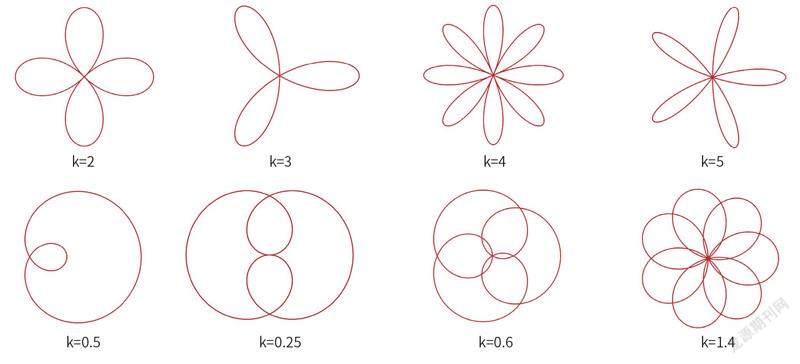
玫瑰曲线（供图/ 张浩）

伯努利的墓碑

17世纪的瑞士数学家雅各布·伯努利（概率论先驱之一，最早使用“积分”术语的人，较早使用极坐标系的数学家之一）醉心于研究对数螺线，他的遗嘱里要求在其墓碑上刻上一正一反两条对数螺线，并附以一语双关的墓志铭“Eadem mutata resurgo（ 纵然变化， 我依如故）”。

“怪异”曲线里的奥妙

魏尔斯特拉斯函数

科赫雪花曲线

在魏尔斯特拉斯函数的影响下，许多“怪异”曲线涌现出来。瑞典数学家科赫给出了著名的科赫曲线，它是人为构造的第一个具有局部和整体相似结构的曲线。

为什么说是人为构造的？你可以在纸上画一条线段，将线段分成三等份，取中间一段为边向外作一个正三角形，并把中间一段擦掉，再分别对得到的每条线段重复上面的过程，画出更小的正三角形后擦掉中间的一段，按此步骤一直迭代（即在前一步的基础上，重复相同的操作）下去，得到的就是科赫曲线。由3 条科赫曲线可以得到科赫雪花曲线。科赫曲线可被用来模拟海岸线。值得注意的是，科赫曲线在任意小的尺度上都具有精细结构，即不管怎么放大总能发现新世界。

科赫雪花曲线迭代过程

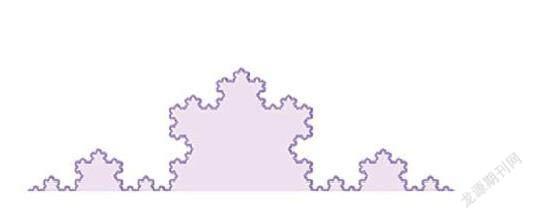
科赫曲线（供图/ 张浩）

科赫雪花曲线（供图/ 张浩）

魏尔斯特拉斯函数的近似图形（供图/ 张浩）

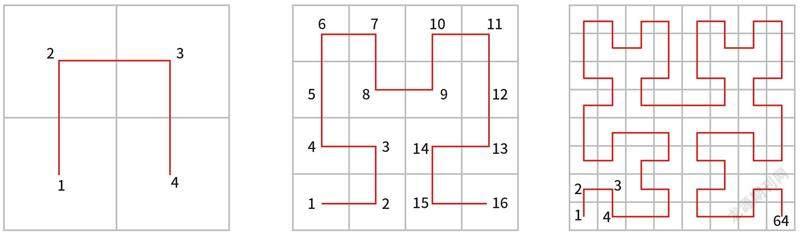
希尔伯特曲线构造示意图（供图/ 张浩）

皮亚诺曲线和希尔伯特曲线

意大利数学家皮亚诺和德国数学家希尔伯特都构造出一条能填满正方形的曲线：通过恰当选择参数函数得到一条连续的参数曲线，当参数变化时，曲线能经过一个正方形内的所有点，相当于能填满一个正方形！

以希尔伯特曲线为例：取一个正方形并且把它分出4 个相等的小正方形，然后从左下角的正方形开始至右下角的正方形结束，依次把小正方形的中心用线段连接起来；下一步把每个小正方形分成4 个相等的正方形，然后依照相同的方式把它们的中心连接起来……将这种操作无限进行下去，最终得到的极限情况的曲线就可以填满整个平面。

“分形”创造出的奇妙函数曲线

分形一词是数学家曼德勃罗创造的，他系统深入地研究了银河系中天体分布、月球表面、地貌的生成、海岸线的结构等自然界中的分形现象。从一个简单的迭代函数f（z）z²+c（z和c都是复数）出发，就能得到许多漂亮的分形图。

让c固定，令z变化起来，能够使函數值不发散的初始值z的集合，即在迭代的过程中使函数值能够稳定在一个范围内z的集合，就叫作朱利亚集。当取不同的c时，对应的朱利亚集就是许多美妙的图形。

如果固定迭代的初始值z₀，让参数c变化起来，能够使函数值不发散的c的集合，就叫作曼德勃罗集。如取初始值z₀=0时，曼德勃罗集中也会出现一个“心形”围成的曲线，若把图形放大，会在图中看到无限多个类似的心形！

作为刻画现实世界最重要的数学模型，函数当之无愧是数学里的绘画大师。也许现在的你对它还有很多难以理解的地方，但不要紧，先看到它的美，再试着去探索它的奥秘吧！还有更多美丽的图形等待你的发现。

（责任编辑 / 张丽静 美术编辑 / 周游）

知识链接 分形

分形具有以非整数维形式充填空间的形态特征，通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”，即具有自相似的性质。

c≈-0.12+0.74i 的朱利亚集，形似一只兔子（供图/ 张浩）

曼德勃罗集