应用数学期望计算概率

合肥市第七中学(230001) 李毅然

通常情况下,我们会通过随机变量的分布列计算随机变量的期望,实际上,我们也可以反过来利用数学期望计算概率.

问题甲箱的产品中有5 个正品和3 个次品,乙箱的产品中有4 个正品和3 个次品.

(1)从甲箱中任取2 个产品,求这2 个产品都是次品的概率;

(2)若从甲箱中任取2 个产品放入乙箱中,然后再从乙箱中任取1 个产品,求取出的这个产品是正品的概率.

参考答案解法:

(1)P{2 个产品都是次品}=

(2)设事件A为“从乙箱中取一个正品”,事件B1为“从甲箱中取出2 个产品都是正品”,事件B2为“从甲箱中取出1 个正品,1 个次品”,事件B3为“从甲箱中取出2 个产品都是次品”.事件B1,事件B2,事件B3是样本空间Ω 的一个分割.

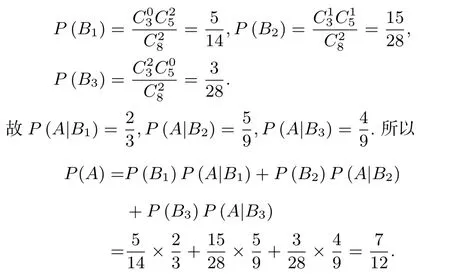
对于本题的第二小问可以有更一般、更简洁的做法,我们先证明如下引理.

引理袋中装有N只球,其中白球数为随机变量,其数学期望为n(n是实数),则从该袋中摸一球得到白球的概率为

这个引理告诉我们可以利用数学期望来计算一些概率问题,实际上利用该引理及递推公式可以解决一些很复杂的古典概型概率计算问题.

对于开头的问题的第二小问,我们可以有如下解法.

解设从甲箱中取出的正品数为X,乙箱的正品数为Y,则显然有Y=X+4.易知X服从超几何分布,

例1甲袋中有a只白球,b只黑球.乙袋中有α只白球,β只黑球.现在从甲袋中随机摸出c(c≤a+b)只球放入乙袋中,求从乙袋中再摸一球为白球的概率.

解记X为从甲袋中所摸c只球中的白球数,则X服从超几何分布,且E(X)=.此时乙袋中共有α+β+c只球,其中白球数α+X是一个随机变量.由引理可得

例1 是前述问题的推广.

例2甲袋中有a只白球b只黑球,乙袋中有c只白球d只黑球.从两袋中各摸出一球,并交换放入另一袋中,这样做了n次之后,再从甲袋中摸出一球,求这球是白球的概率.

解设Xi,Yi分别表示交换i次后甲、乙两袋中的白球数,显然有Xi+Yi=a+c.用ξi,ηi分别表示第i次的交换情况

利用例2 可以很容易解决2020 年江苏高考理科卷的最后一题.

例3(2020 年高考江苏理科卷)甲口袋中装有2 个黑球和1 个白球,乙口袋中装有3 个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n次这样的操作,记甲口袋中黑球个数为Xn,恰有2 个黑球的概率为pn,恰有1 个黑球的概率为qn.

(1)求p1,q1和p2,q2.

(2)求2pn+qn与2pn−1+qn−1的递推关系式和Xn的数学期望E(Xn)(用n表示).

很多时候我们总是利用随机变量的分布列来求它的期望,现在从前面的例子可以看出有时也可以反过来利用期望来求一些概率.