面向CJ15 卧式湿法研磨机的CFD-DEM耦合仿真分析
吴 波,孙 飞,何 康,杨 权,李小标,蔡 斌,西成才
(1.宿州学院a.机械与电子工程学院;b.高端微纳研磨装备校企协同创新工程中心,安徽 宿州 234000;2.安徽儒特实业有限公司,安徽 宿州 234000)
在纳米粉体生产方面, 湿法研磨不仅避免了化学法制造纳米粉体的高成本缺陷, 也避免了机械干法研磨细度难以达到纳米级粉体的不足, 是业界公认的最有效且最合乎经济效益的纳米级粉体制备方法。 湿法卧式研磨机是目前常用的超细粉碎设备[1]。 国内外很多学者采用数值模拟的方法探索了磨机内部研磨过程中运动状态和能量环境。 Jayasundara 等[2-3]利用CFD 对搅拌细磨装备内部矿浆和介质的运动状态进行了分析,Yang 等[4]使用离散单元法(DEM)对宏观和微观的粒子流在水平旋转辊磨中不同区域内的行为进行了系统分析,Sinnott 等[5]借助DEM 和PEPT 的仿真手段对介质和研磨性能的关系进行了研究,杨涛等[6]借助于ANSYS软件建立了大型半自磨机的有限元模型,赵艳平[7]利用FLUENT 软件对卧式搅拌磨内部流场进行了模拟。
但是物料和介质在磨机中怎样运动,其流场情况和颗粒场情况如何,物料粉碎规律与操作条件的关系怎样,各实验条件对能耗有何影响,这些都需要深入进行研究。 本文以安徽儒特实业有限公司生产的CJ15 卧式湿法研磨机为研究对象,利用CFD-DEM 流固耦合方法对农药混悬液研磨过程进行仿真模拟,进而对流场速度规律、颗粒场能量变化规律进行分析。
1 数值模拟
在实际研磨时, 研磨机内部主要是流固混合状态的研磨介质和颗粒间的相互作用, 本文采用计算流体力学(CFD)与离散元(DEM)耦合的方法分析流体相与颗粒相间的相互作用。数值模拟步骤为:(1)三维建模;(2)流场数值模拟设置;(3)颗粒场设置;(4)在FLUENT 中导入耦合文件,与EDEM 建立连接,开始耦合计算。
1.1 三维建模
安徽儒特实业有限公司生产的CJ15 卧式湿法研磨机, 转子为涡轮转子, 采用Solidworks 三维建模软件对模型进行去圆角和去倒角处理, 去除扩散轮, 不设置进出口, 所有部件均进行等比例缩小,缩小后其有效研磨容积为0.03 L,筒体内壁直径为32.85 mm, 研磨筒内壁轴向长度为47 mm,转子直径为26.88 mm,搅拌轴直径为11.8 mm,简化后的三维模型如图1 所示。

图1 简化后的三维模型
1.2 流场设置
在Workbench 平台中调用 “Fluid Flow(Fluent)”模块,依次完成仿真模型设置、网格划分和求解计算。
1.2.1 仿真模型设置
启 动 “DM”, 将 简 化 后 的 三 维 模 型 导 入“Geometry”,将计算域分成动态区和静态区两部分,将动态区和静态区设置为“Fluid”类型,仿真模型如图2 所示。
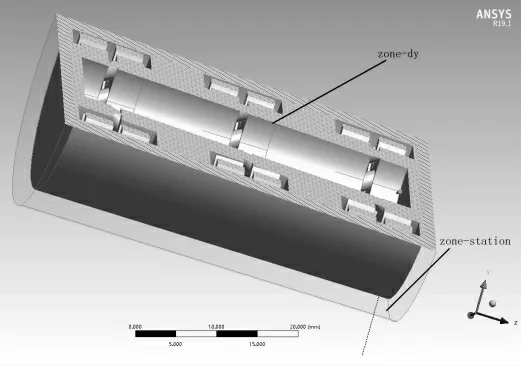
图2 仿真模型
1.2.2 网格划分
为提高计算效率和计算速度,采用结构化网格。研磨区网格划分的网格数量为261 888 个(图3)。

图3 网格划分全剖图
1.2.3 求解计算
选择标准k-ε 湍流模型, 以农药悬浮液作为研磨对象, 根据农药生产厂家提供参数设置材料属性, 设置农药密度为1 050 kg/m3, 动力黏度为0.4 Pa·s。 对于旋转的流体耦合仿真, 选定压力Coupled 耦合求解的控制方程进行求解。 对于研磨机的高速旋流,采用PRESTO!压力的插值方法进行求解。
1.3 颗粒场设置
1.3.1 添加研磨介质
介质球颗粒的大小决定了介质球与物料碰撞接触点的数量。结合生产实际综合考虑,选择研磨介质直径为0.8 mm,材质为氧化锆。
1.3.2 定义几何体参数
因为EDEM 三维建模能力较弱,所以研磨转子、内筒和颗粒都将通过导入的方式添加。 将ANSYS 生成的研磨转子和内筒的 “FFF.msh” 文件直接导入EDEM,并赋予氧化锆的材料特性;将在Solidworks 软件中画好的颗粒以“.igs”格式导入EDEM,导入后生成的几何体模型如图4 所示。

图4 几何体模型图
按照质量生成方式设置颗粒参数。本文中将颗粒填充率设置为60%, 总生成颗粒质量为0.065 2 kg, 生 成 速 度 为0.032 6 kg/s, 设 置 颗粒下降速度为1 m/s,方向为X 正方向,转子开始转动时间设置为2.3 s,重力方向设置为X 正方向。
2 仿真结果及分析
物料的研磨主要来自物料与研磨介质之间的碰撞,研磨效率、研磨介质颗粒与物料之间的接触力、碰撞频率和碰撞强度都有着直接的关系。 仿真研究从探究研磨发生的主要区域、研磨过程中研磨介质碰撞能量的变化情况入手。
2.1 流场分析
研磨介质的动能直接来自流体, 流体速度梯度较大的地方,研磨介质颗粒的碰撞更加剧烈,分析流体的速度等值线疏密程度可以预测研磨机的研磨效果。 当填充率为60%时, 研磨机转子转速分别为800、1 000、1 200 和1 400 r/min 情况下的速度等势图如图5~8 所示。
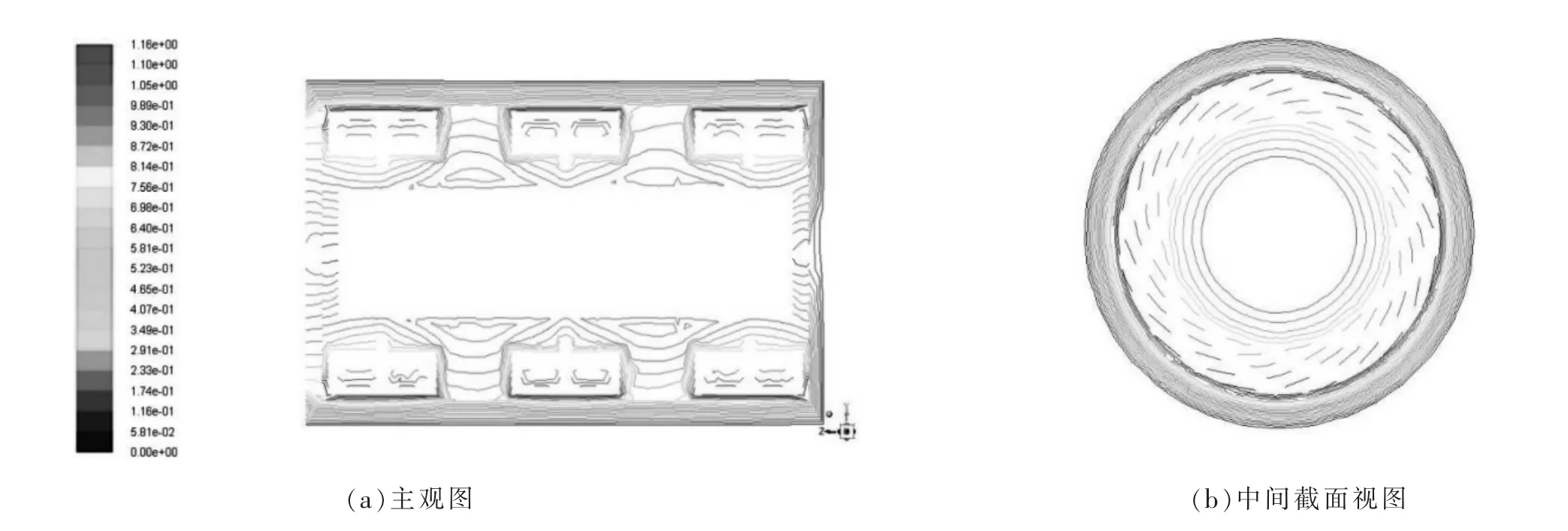
图5 转速为800 r/min 时,研磨区域的速度等势图
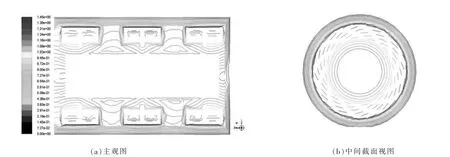
图6 转速为1 000 r/min 时,研磨区域的速度等势图

图7 转速为1 200 r/min 时研磨区域的速度等势图
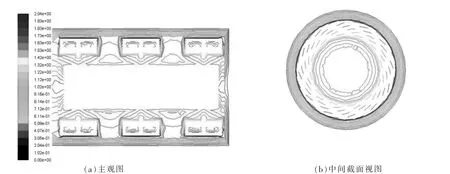
图8 转速为1 400 r/min 时在研磨区域的速度等势图
由图5~8 可知,转子外缘到筒壁之间区域,等势线较为密集,该区域速度变化较大,能量密度较大,此区域应是物料破碎的主要区域;在径向方向,自筒壁至研磨转子外缘之间区域速度等势线逐渐密集,说明速度逐渐增大, 转子边缘区域的流体存在较大动能。
2.2 颗粒场分析
研磨机刚启动时, 研磨介质的总能量等于转子转动产生的动能和流体的动能之和, 而当研磨介质产生碰撞后, 研磨介质的总能量等于介质碰撞能量与研磨介质的动能和。 通过对研磨介质颗粒之间的碰撞能量进行研究,探究提高研磨效率的方法。
研磨介质颗粒之间的碰撞能量等同于EDEM 中能量损失数值, 本文对不同转速下颗粒碰撞产生的总能量损失、 法向能量损失和切向能量损失的数值进行分析。
2.2.1 碰撞总能量对比
通过模拟得到在60%填充率情况下,各转速下颗粒碰撞总能量数据后,分别对得到的数据求平均值, 即可得到颗粒碰撞平均总能量损失。 在转速为800 r/min 时颗粒碰撞平均总能量损失为3.079 2×10-6J;在转速为1 000 r/min 时颗粒碰撞平均总能量损失为2.969 12×10-6J; 在转速为1 200 r/min 时颗粒碰撞平均总能量损失为2.139 55×10-6J;在转速为1 400 r/min 时颗粒碰撞平均总能量损失为2.657 34×10-6J。 根据以上数据绘制出不同转速下平均碰撞总能量对比折线图,如图9 所示。 由图9知,颗粒碰撞平均总能量损失并不是随转速提高呈线性增长的,当转速为1 200 r/min 时,损失能量最小。 因此,对于本涡轮转子研磨机而言,在颗粒填充率为60%、 转速为800~1 000 r/min 时, 研磨效率较高。

图9 60%填充率情况下不同转速下碰撞总能量对比
2.2.2 切向和法向碰撞能量对比
物料的粉碎总体上是通过介质球之间的碰撞实现的。 转子开始转动以后,各转速下研磨介质颗粒切向碰撞能量和法向碰撞能量数据(总模拟时间的碰撞能量的平均值)变化情况如图10 所示。由图10 可知,切向碰撞能量与法向碰撞能量的比值近似为8∶2,研磨介质颗粒平均切向碰撞能量远大于平均法向碰撞能量,因此切向碰撞起主要研磨作用。

图10 不同转速下平均切向和法向碰撞能量对比
3 结论
针对CJ15 卧式湿法研磨机CFD-DEM 耦合模拟仿真,主要研究结果如下:
(1)研磨机转子外缘到筒壁之间区域为研磨破碎的主要区域;
(2)在填充率60%、转速为800~1 000 r/min 时研磨介质碰撞总能量最大,研磨效率最高,但是转速1 200 r/min 为拐点,研磨介质碰撞总能量最小。
(3)研磨介质颗粒的切向碰撞能量始终大于法向碰撞能量,能量比例近似为8∶2,切向力在研磨过程中起主要作用。

