伺服阀小开口的流量非线性特征
蒋博文,张振华,王飞, 延皓
(1.北京特种机械研究所,北京 100143;2.北京交通大学机械与电子控制工程学院,北京 100044)
0 前言
对于国防工业领域和一般工业领域的伺服运动控制,电液伺服阀是重要的核心元件。目前伺服阀的主阀芯一般采用滑阀形式,在实际闭环控制系统中,主阀芯往往处于小开口工作状态。当作动器速度逐渐下降,阀开口不断减小,在大负载的情况下常常出现系统振动,这可推测为伺服阀小开口非线性和伺服系统非线性共同作用的结果[1]。
吴正江[2]对环形圆缝阀口流动特性进行了研究,并进行了数值模拟,给出了伺服阀压力流量、雷诺数和流量系数之间的关系。张丽[3]考虑阀口棱边几何误差对滑阀性能的影响并做了仿真研究,同时讨论了不同阀芯棱边对流量系数的影响。蔡霖[4]对各类情况下滑阀性能进行了仿真研究,提到了流量系数的变化趋势。冀宏等人[5]对滑阀矩形节流槽阀口的流量系数进行了详细的讨论和数学分析,为之后的研究开辟了新的方向。金晓宏等[6]针对伺服阀滑阀阀口系数影响因素进行了分析。而范家辉[7]针对滑阀流场特性与间隙泄漏开展了研究,并给出了滑阀配合间隙的泄漏量模型。霍卫杰[8]基于滑阀流量压力特性的伺服阀配磨系统进行研究,其中以层流和流态过渡的方式讨论了伺服阀的内泄漏。
针对伺服阀阀口打开过程中流态变化引发的非线性,本文作者提出一种新的理论模型,描述和解释了伺服阀小开口时的非线性现象,并通过试验进行了证明[9-10]。
1 滑阀节流的流动形态演变
当零开口伺服阀阀芯处于零位时,主阀芯和阀套之间存在泄漏流量,流态为层流状态[11];当阀芯节流口逐渐打开(如图1所示),流动将在某个阶段演变为湍流,且流量系数为恒定值,此时伺服阀的流量才呈现为线性特性,并作为线性元件服务于液压伺服系统。
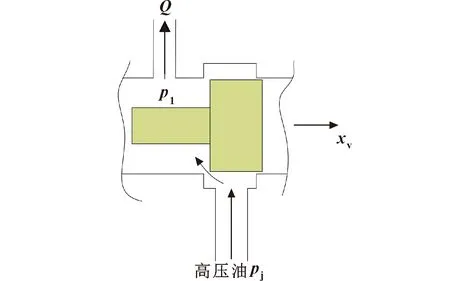
图1 滑阀节流口的打开
层流到湍流的演变并不是突然发生的。如果流态是突变的,那么在节流口打开的过程中,会出现流量“断崖”,即流量系数发生突变,这与实际情况并不相符。因此,这种流态变化存在一个过渡过程,体现为流量系数的连续变化。
1.1 零位流动
当阀芯处于零位时,泄漏的主要流动形式是圆环间隙内的层流流动。此时的流量即为阀中位泄漏量,计算公式[12]为
(1)
其中:b为缝隙高度,m;c为有效环形周长,m;μ为油液动力黏度,Pa·s;pj-p1为单边阀压降,MPa。
此时流过的截面面积为
A0=cb
(2)
此时的流动雷诺数为
(3)
其中:ρ为液压油密度;v0为当前流速,v0=Q0/A0。
如《掌声》这篇课文,教学重点是了解掌声是在什么情况下响起来的,感受掌声带给英英的变化,从而体会同学们对英子的鼓励与关爱。在执教这一课时,我紧紧围绕教学重点来设计问题:
1.2 小开口层流
而当阀芯节流口刚刚打开时,流动仍然处于层流状态,由于阀芯位移的产生,通流截面发生了改变,因此式(1)可修改为
(4)
其中:xv为阀芯位移。
定义小开口层流的等价流量系数为
(5)
其中:A1为小开口时的开口面积。
(6)
将式(4)、式(6)代入式(5)得:
(7)
此时流动雷诺数为
(8)
其中:v1为当前流速,v1=Q1/A1。
根据式(5)和式(8)可得:
(9)
将式(7)和式(9)相乘可得:
(10)
1.3 大开口完全湍流
取临界雷诺数为260(根据文献[13])。随着阀开口的逐渐变大,当流动雷诺数大于此值,认为流态为完全湍流状态[14-15],此时流量公式为一般节流公式:
(11)
其中:Cd3为流量系数;A3为通流面积,A3≈wxv。

1.4 从层流到完全湍流的过渡过程
当雷诺数到达某个数值(即层流的最大雷诺数Relmax),流动开始从层流向湍流过渡,根据式(10)此时流量系数为
(12)
(13)
1.5 关于流量系数讨论

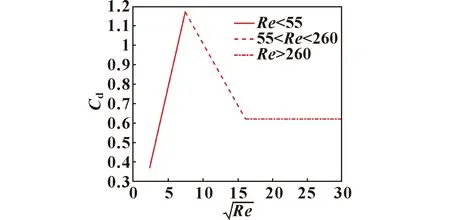
图2 流量系数与雷诺数的相关性
2 试验验证
为验证小开口流量系数模型的正确性,设计如图3所示的试验系统,以测量伺服阀的某节流边的流量。测试时,阀的P口压力由一个减压阀调节,然后给阀不同的开口指令,并通过流量计测量A口流量。油源系统和试验平台见图4和图5。

图3 测试原理 图4 油源系统 图5 试验平台
采用10号航空液压油,试验温度为15 ℃,伺服阀P口压力设定为2.5 MPa,回油单向阀的压力为0.05 MPa,试验结果见图6。
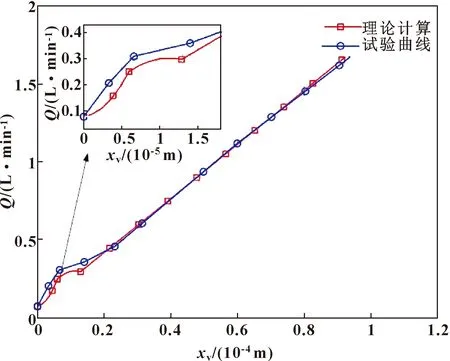
图6 试验结果与理论计算
按照文中所提流量系数模型(如图2所示),并根据相关参数(如表1所示)也可计算得到阀口逐渐打开时的流量特性(如图6所示)。相比之下,理论计算的流量特性与试验结果是一致的,因此该模型能够解释小开口时阀增益偏大的现象。另一方面,在阀口刚刚打开时,该模型理论计算得到的流量稍小,这可能与小开口时非全周开口阀的圆周向流动有关。

表1 理论计算相关参数
试验曲线和理论计算表明:在阀芯位移0.06 mm以下,流量曲线呈非线性且斜率较大,即流量增益大于大开口工况;当阀芯位移大于0.22 mm,流量曲线呈现线性,即流量系数收敛到固定值;在0.06~0.22 mm之间,曲线斜率较低,为2种状态的过渡过程。因此,流量增益在阀口逐渐打开过程中是波动的。由于在伺服阀处于小开口时流量增益偏大,当重载伺服系统逐渐停止时,伺服阀处于小开口状态,有可能诱发系统稳定性的下降,从而导致振动的发生。
3 结论
受到流态变化影响,在伺服阀节流口逐渐打开的过程中,其流量系数并不恒定。文中提出一个流量系数模型,解释了节流流动从层流到湍流变化过程中流量系数的变化规律。理论模型和试验表明:在小开口时阀的流量特性呈现一定的非线性,且具有更大的流量增益。为保证系统低速稳定性,应在电液伺服系统设计时考虑小开口流量增益的增大问题,为系统提供充分的稳定裕量,从而避免振动的产生。

