面向狭小环境检测的柔性机器人运动建模与控制研究
张恒,齐飞,,窦小明,姜加伟,白东明,裴海珊,朱靖
(1.常州大学机械与轨道交通学院,江苏常州 213000;2.快克智能装备股份有限公司,江苏常州213000;3.金华职业技术学院机电工程学院,浙江金华 321000)
0 前言
针对复杂狭小非结构化环境中的检测需求,传统刚性机器人由于体积大、自由度低及灵活性差等缺陷难以直接应用[1]。而连续体机器人因具有灵活性、柔顺性及安全性等方面的优势,相比于传统刚性机器人在一些未知狭小非结构化的环境中得到了广泛应用和深入研究。由多段可弯曲单元组成的机械臂可以适应各种复杂未知的狭小环境,同时也可以通过自身的弯曲变形进入到传统机器人无法到达的狭小缝隙之中实现任务操作,如医疗微创手术、飞机油箱检修及核工业管道探测等领域。
NEPPALLI、MCMAHAN等[2-3]一起研制了Air-Octor连续体机器人,该机器人通过在褶皱管内充气来支撑其结构,并通过3根绳索驱动机器人实现2个自由度的运动。美国约翰霍普金斯大学的ALAMBEIGI 团队设计了一种新型的弯曲可控钻头手术工具,弯曲角度可达 40°,能够实现 S 形的弯曲变形,解决了传统的刚性机械无法到达股骨整块区域的问题[4]。Festo公司研制了一种气压驱动的仿生象鼻操作手[5],可通过弯曲和伸展进行抓取、搬运等工作,实现对易碎与不同形状的物体进行无损抓取。OC Robotics公司设计的蛇形连续体机器人应用于核工业管道探测和维修,提高了检测效率和人员安全性[6]。
付宜利等[7]设计的SMA驱动连续体机器人可根据电流的大小实现不同角度的弯曲。XU等[8]研制出基于高刚度可形变蛇形连续体手术器械的单孔腹腔镜手术系统。牛国臣和张云霄[9]研制的一款绳驱连续体机器人能够很好地完成飞机油箱检测任务。王俊[10]设计的多关节绳驱连续体机器人具有质量轻、转动惯量小和便于实现控制等优点。陈柏等人设计的航空发动机叶片原位检测绳驱动机器人能够根据发动机内复杂环境作出相应的变形,从而实现对发动机的原位检测[11]。综上所述,相较于其他驱动方式,绳索驱动控制可实现核心零部件与使用环境相隔离,便于零部件的换装与维修,能适应环境恶劣的工作场所。
连续体机器人因其形状由若干段连续曲线表征,导致其末端精确定位困难,弯曲姿态难以获得[12-13],也进一步导致其控制精度较差。IVANESCU等[14]根据章鱼臂的弯曲动作,提出了描述章鱼臂缠绕物体的方程,并对其动力学进行了深入研究。TRIVEDI等[15]通过Cosserat Rod理论建立的连续体运动学模型能够对机器人的变形进行精确的描述,这主要是由于该模型综合考虑了材料特性、负载等因素。MELINGUI等[16]在对神经元定性分析的基础上,提出了连续体机器人的运动分析模型。GRAZIOSO等利用微分几何和指数坐标分析连续体机器人变形时形成的正切螺旋线,提供了直观有效的构型描述[17]。SU等[18]提出了一种精确几何模型用于描述同心管连续体的运动。KOUNO等[19]采用多段曲线的组合描述连续体机器人。上述模型大多涉及了高阶微分方程的解算和复杂的材料力学理论分析,计算量较大,实时控制困难。目前,由于连续体机构的变形接近于常曲率变形,大多连续体机器人的运动模型多在常曲率圆弧假设下进行描述,这不仅降低了连续体机器人运动建模的难度,同时能够实现机器人末端位姿较为准确的运动控制。
在对狭小环境进行检测时,传统刚性机器人工作空间受限,不能适应非结构化的空间,具有诸多局限性,难以完成作业任务。为此,本文作者设计一种绳驱动一体化加工而成的连续体机器人,以完成对狭小、非结构化空间的检测、维护、维修等任务。在常曲率假设下,基于几何分析法对机器人正、逆运动学建模,构建其驱动空间、关节空间及操作空间间的映射关系,并以蛇行运动模型和逆运动学为基础控制连续体机器人的介入运动;利用MATLAB对连续体机器人进行运动学仿真,并搭建样机平台,通过实验验证运动模型和运动控制方法的正确性。
1 连续体机器人结构设计
传统组装式连续体机器人多采用以NiTi合金心柱为支撑、多个关节相互串联的结构。当机器人弯曲变形时,在绳索拉力的作用下会产生侧向力,从而使得弯曲单元与中心柱之间产生扭矩[8],使结构发生变形,远离预定位置,最终导致控制精度差、位置误差大等问题。
为避免中心柱结构所产生的误差,采用由电火花线切割一体化加工而成的连续体结构,如图1所示。机器人的弯曲单元为筒状结构,内部空间为末端执行器布线空间,四周的支撑柱,每层分布两个,间隔180°分布,与相邻两层的支撑柱间隔90°错开,以保证主体在任意方向的弯曲性能。两对驱动绳索相互交错布局,每对绳索均由一台电动机控制,当一根绳索伸张一定长度时,另一条绳索则缩短相同的长度,以保证成对的一组绳索绳长变化量相等。因此,该方案仅需两个步进电机便能控制单节柔性弯曲单元2个自由度,减少了电机数量,降低了控制难度,具有较高性价比。连续体机器人的结构参数如表1所示。
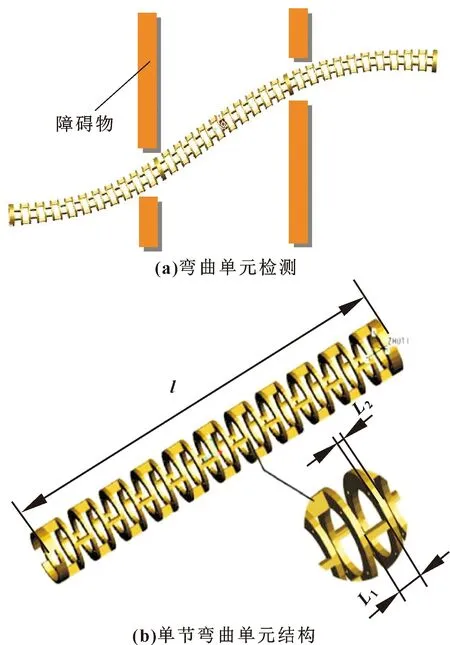
图1 弯曲单元

表1 弯曲单元尺寸参数
1.1 机器人运动学建模
为描述机器人弯曲单元的运动状态,首先对其进行运动学建模,以便于后续运动控制研究。假设连续体机器人在运动时3节弯曲单元均为等曲率变形,且每节弯曲单元由均匀分布的4根绳索(li1,li2,li3,li4)驱动,在第i(i=1,2,3,…,n)节弯曲单元的末端基面上建立关节坐标系Oi-1(xi-1,yi-1,zi-1),而O0(x0,y0,z0)为第一节弯曲单元的初始连接盘坐标系,如图2所示。
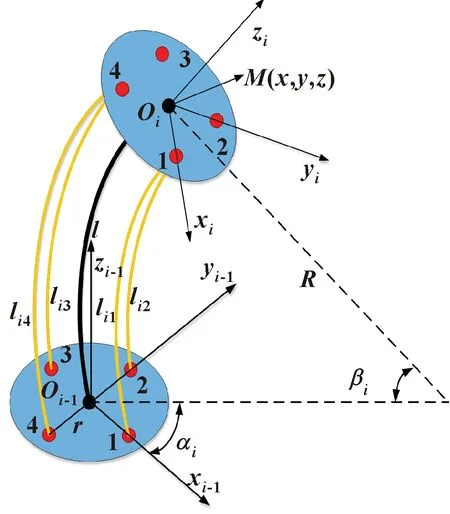
图2 单节弯曲单元模型
假设弯曲单元中心线圆弧对应的半径为R,则弧长与半径的关系为
(1)
假设弯曲单元末端中心点的坐标为M(x,y,z),则在基坐标系下可表示为
(2)
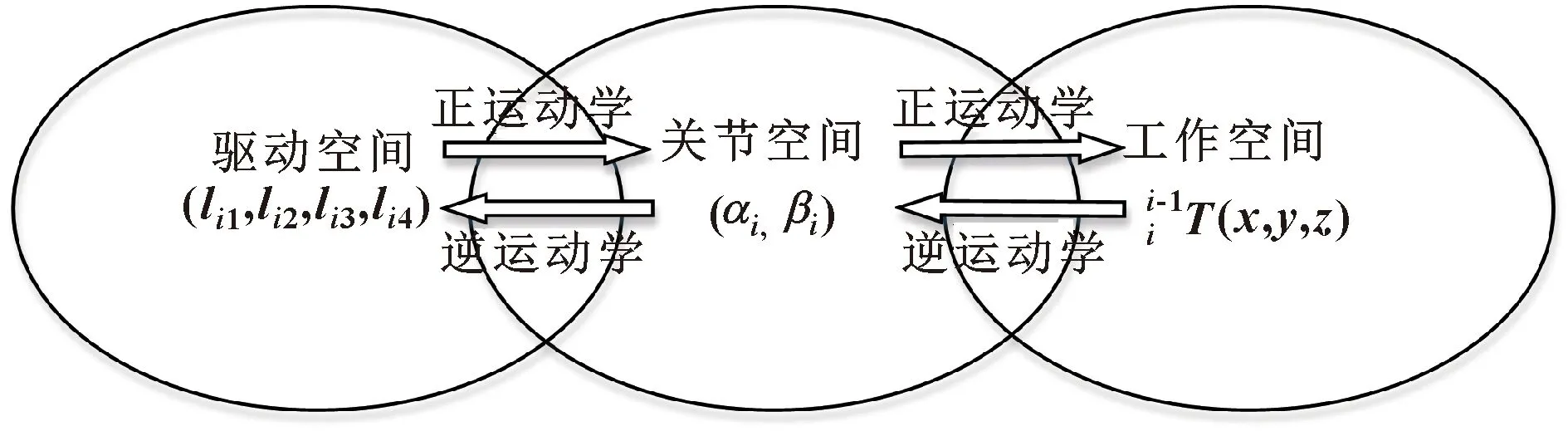
图3 连续体机器人运动空间映射
1.1.1 关节空间-工作空间的映射
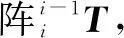
(3)
其中:c为cos函数的缩写,s为sin函数的缩写。将式(3)中的运动关系展开即可得到式(4):
(4)
(5)
1.1.2 工作空间-关节空间的映射
通过上述关节空间到工作空间的正运动学建模,得到它们之间对应的映射关系。下面对其进行逆运动学建模,首先由式(4)得到弯曲单元末端位置(xi,yi,zi)如式(6)所示:
(6)
对式(6)进行求解分析,即可得到αi、βi:
(7)
1.1.3 关节空间-驱动空间的映射
驱动空间的绳长变化将导致关节空间的偏转角αi和弯曲角βi发生改变,在已知αi和βi的情况下,通过几何分析法即可求得对应绳长的变化量。
考虑到每节弯曲单元都由4根驱动绳索,成对的2根驱动绳索相互耦合,当一条绳索伸长,另一条绳索则缩短相同的长度。在已知各个弯曲单元弯曲角度的情况下,根据几何分析可知,各个驱动绳索长度如式(8)—(11)所示,绳索变化量如式(12)—(15)所示:
li1=l-rβicosαi
(8)
(9)
li3=l+rβicosαi
(10)
(11)
Δli1=rβicosαi
(12)
(13)
Δli3=-rβicosαi
(14)
(15)
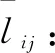
(16)
1.1.4 驱动空间-关节空间的映射
驱动空间到关节空间映射的过程量为Δl,即通过改变驱动绳索的长度使αi和βi的值产生变化,在已知各个弯曲单元驱动绳索长度(li1,li2,li3,li4)的情况下,结合式(8)—(11),即可求得各个弯曲单元的αi和βi:
(17)
(18)
1.2 工作空间仿真分析
根据前文所建的运动模型,对连续体机器人的工作空间进行仿真分析,以验证模型的准确性。假设机器人单节弯曲单元的长度为200 mm,弯曲单元的偏转角范围为0°~360°,弯曲角范围为0°~90°。对由3节弯曲单元构成的连续体机器人进行运动仿真,其总长为600 mm,总偏转角与单节偏转角相一致,范围为0°~360°,总弯曲角为单节弯曲角的叠加,范围为0°~270°。对机器人工作空间进行仿真,根据关节空间和工作空间的映射关系,通过MATLAB软件进行程序编程,即可得单节、双节和三节的工作空间和yOz视图,如图4—图6所示。
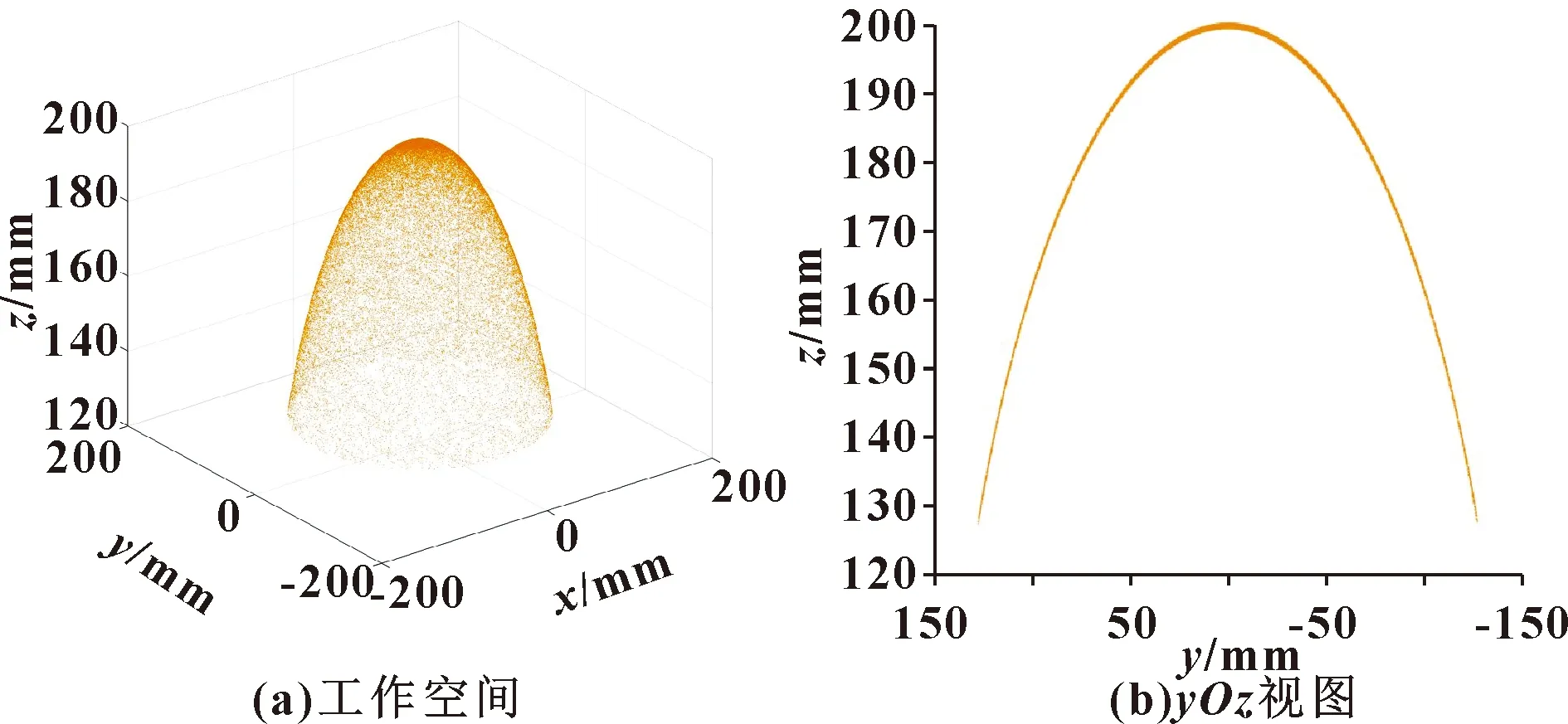
图4 单节弯曲单元工作空间
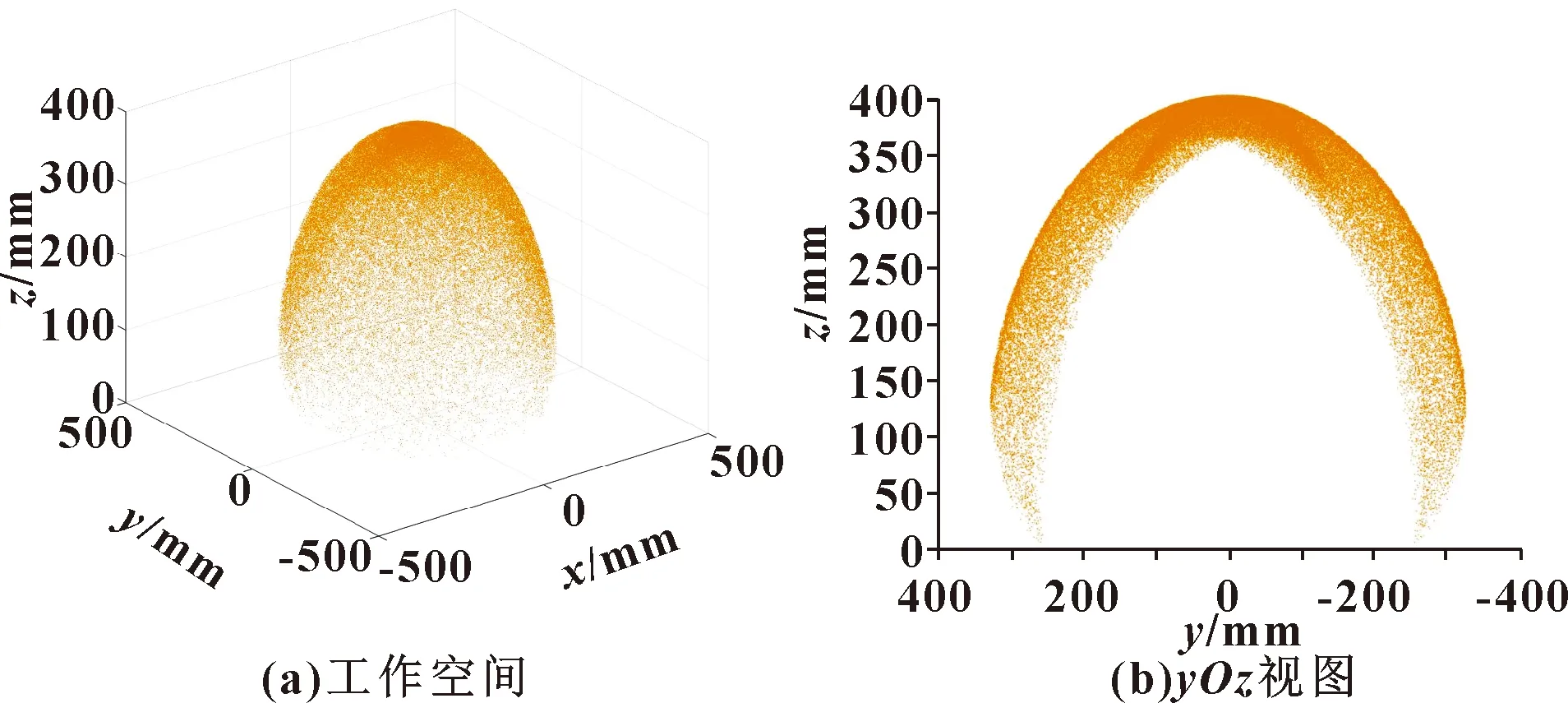
图5 双节弯曲单元工作空间
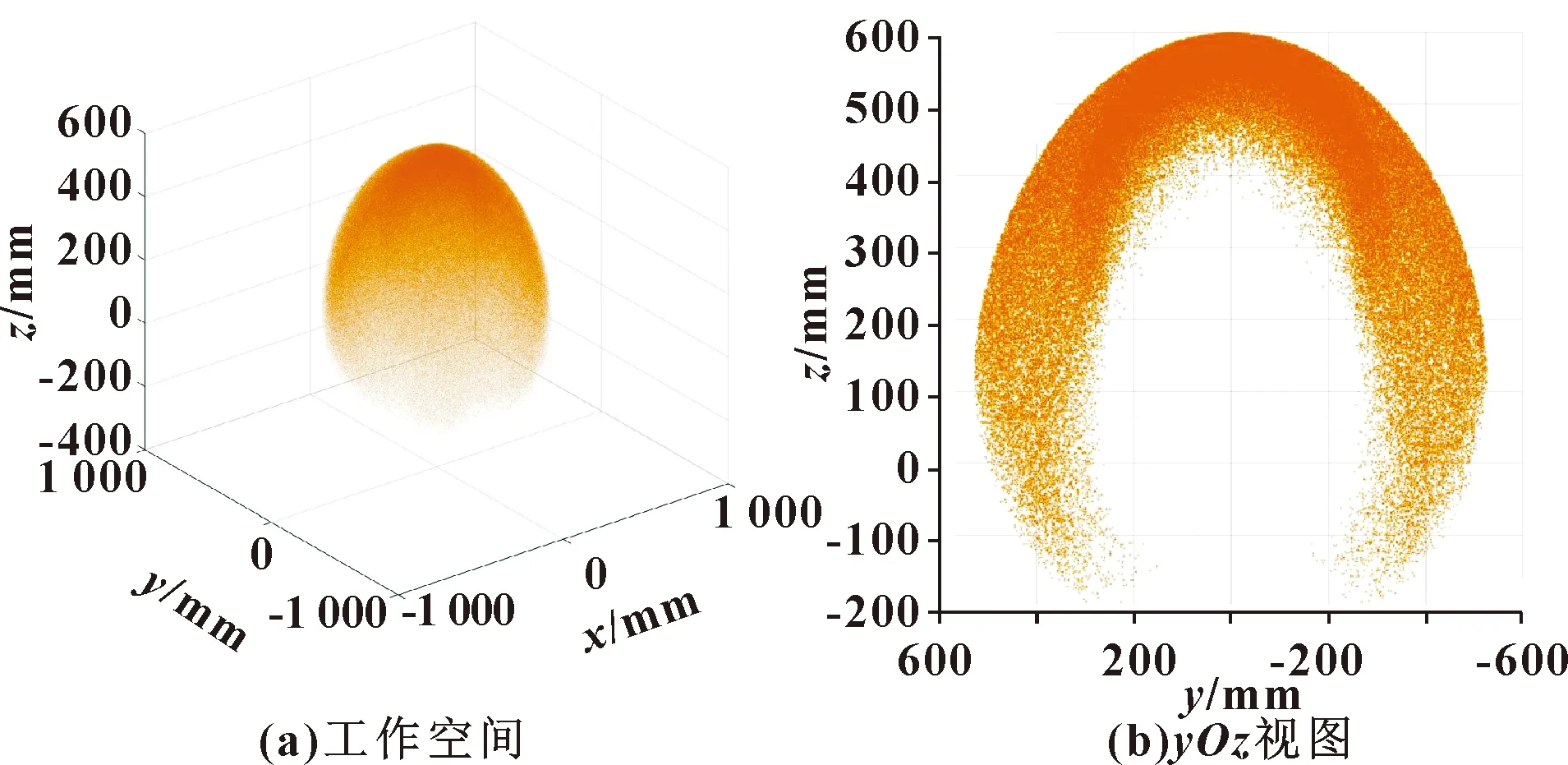
图6 三节弯曲单元工作空间
1.3 工作空间位姿仿真分析
为验证所建运动学模型的正确性,对4种不同状态的位姿进行仿真分析。4种状态分别为
G1{α1(90),α2(60),α3(45),β1(60),β2(45),β3(30)}
G2{α1(90),α2(60),α3(90),β1(60),β2(45),β3(30)}
G3{α1(90),α2(45),α3(90),β1(60),β2(45),β3(30)}
G4{α1(45),α2(90),α3(45),β1(60),β2(45),β3(30)}
其中,设定G1和G2的前两节位姿状态相同,G1、G2和G3的第一节位姿状态相同,G4与其他3种位姿状态都不相同。机器人仿真结果如图7所示。可知:状态G1和G2的前两节弯曲单元的位姿状态重合,G1、G2和G3的第一节位姿状态重合,G4与其他3种状态均不重合,由此验证了运动学建模的可行性。
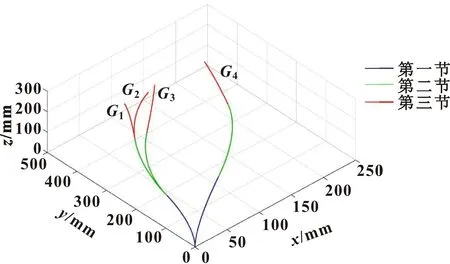
图7 不同状态位姿仿真结果
1.4 驱动空间仿真分析
假设连续体机器人的初始状态为竖直形态,此时的机器人初始端坐标为{0,0,0},末端坐标为{0,0,600}mm,下面对3节弯曲单元进行运动学仿真。设定β1、β2、β3的值分别为90°、90°、90°,然后对α从0°~360°的过程中3节弯曲单元中4条绳索的变化量进行仿真分析。
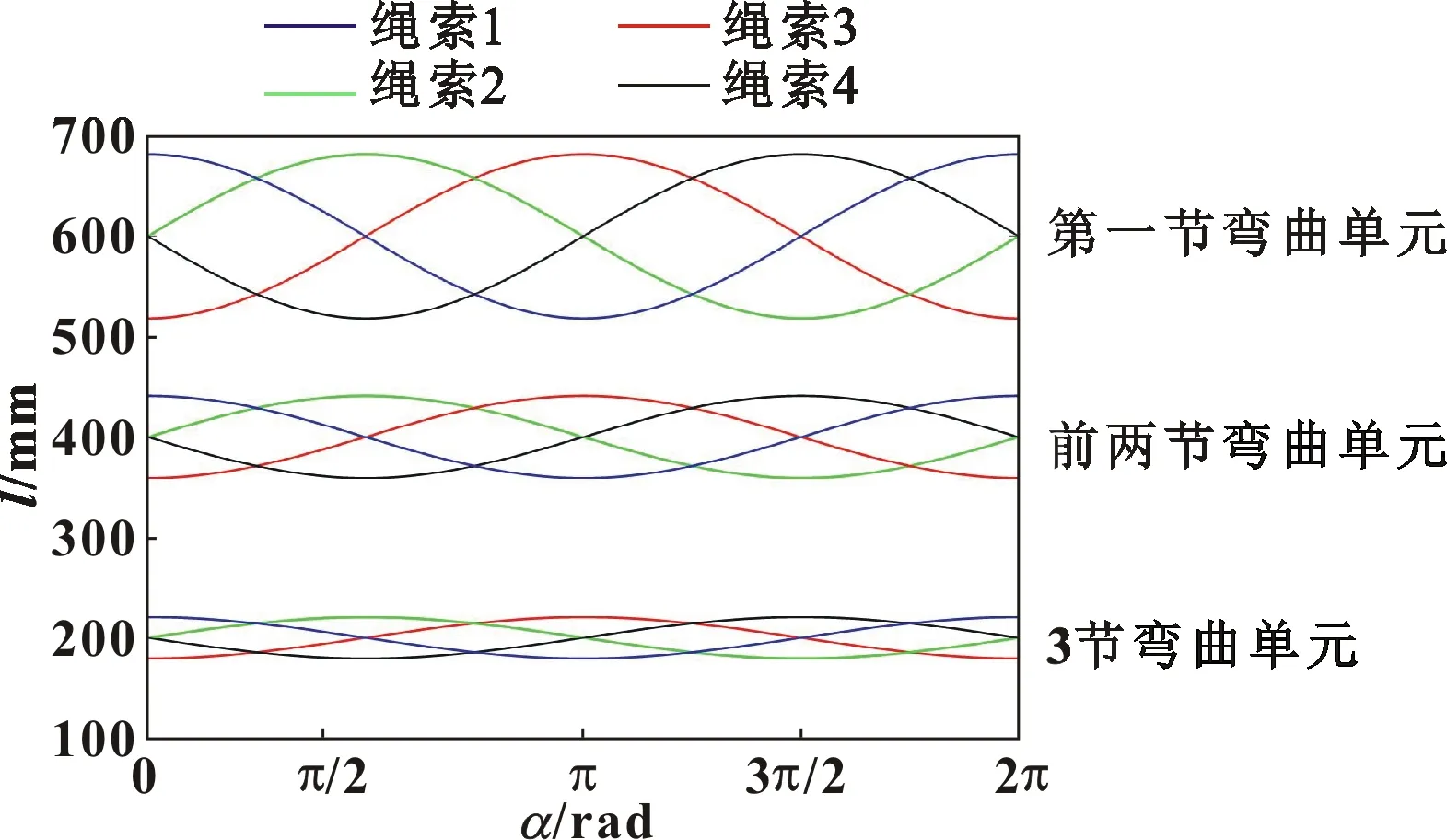
图8 3节弯曲单元偏转绳长变化
假设α1、α2、α3的值均为60°,然后对β从0°~90°的变化过程中3节弯曲单元中4条绳索进行仿真。
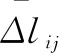
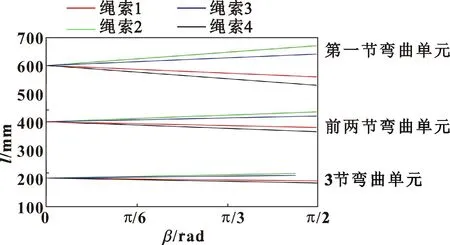
图9 3节弯曲单元弯曲绳长变化
2 机器人运动控制
2.1 控制方案
为实现连续体机器人的运动控制,搭建如图10所示的控制系统,主要包括单片机、摄像头、LCD屏、步进电机等。单片机选用STM32F103ZET6,其优势在于能够进行大量的浮点数运算,且能很好地支持彩屏显示。首先通过上位机将控制信息发送至单片机,然后进行数据处理并驱动相应电机运转,从而带动摆臂牵引绳索,最终实现连续体机器人的运动控制。另外,为满足对狭小环境的探测需求,在连续体机器人运动的同时,安装于机器人末端的摄像头实时地将机器人末端图像通过单片机传输至LCD屏,以实现对狭小环境的探测。
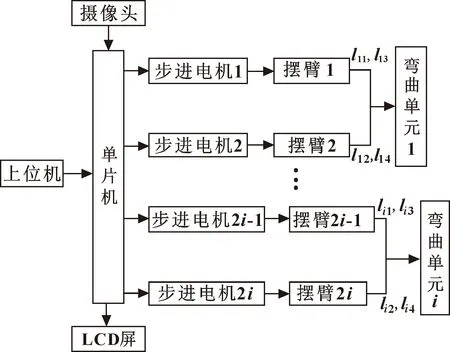
图10 控制系统框图
2.2 控制方法
根据所建的机器人运动学模型,可控制机器人的弯曲运动,但在面对狭小环境检测时,为避免触碰障碍物时对机器人造成损坏,应减少与规划路径间的偏差。本文作者采用蛇形运动控制算法,让后一节弯曲单元沿着前一节弯曲单元的路径前行,控制后一节弯曲单元的姿态参数与前一节单元重合路径的姿态参数相同,便可使得两者路径重合。这样只需控制最后一节弯曲单元沿规划路径前行即可,简化了计算过程且提高了机器人的运动效率。
具体控制过程如下:
(1)将机器人末端定位至路径起点;
(2)向前行进一步;
(3)控制后一节弯曲单元与前一节重合路径姿态参数相同;
(4)判断机器人是否完全重合路径,如完全重合,即整个运动完成,如未重合,则重复步骤(2),直至完全重合。图11所示为连续体机器人沿着规划路径前行的过程。
图11 运动控制图
3 实验平台搭建与分析
3.1 系统整体图
为验证文中所建运动学模型及控制方法策略的有效性和准确性,通过3D打印技术搭建了单节连续体机器人实验样机平台,以进行相关运动性能实验验证。所设计的连续体机器人系统样机如图12所示,该系统主要包括单节机器人弯曲单元、PC机、摄像头单元、LCD显示单元、主控芯片单元、电源、驱动电机单元等。

图12 机器人系统
摄像头单元与主控芯片单元间的走线布置于弯曲单元的中空腔内,能有效减少走线对弯曲单元运动的影响。在底座的设计中,为各个零部件都设计了安装位置,紧凑的布局设计使得机器人系统小巧便携。为使得操作更加高效,将显示屏放置于底座顶部,使操作人员在控制弯曲单元运动的同时能够通过显示屏观察到弯曲单元末端周边环境。
3.2 空间旋转运动实验
对连续体机器人进行空间旋转实验,如图13所示。在控制弯曲角为90°的状态下进行空间旋转运动,并用坐标纸对偏转角进行测量,取4组数值0°、90°、180°、270°进行理论值与实际值对比分析,结果如图14—图15所示。

图13 空间旋转实验
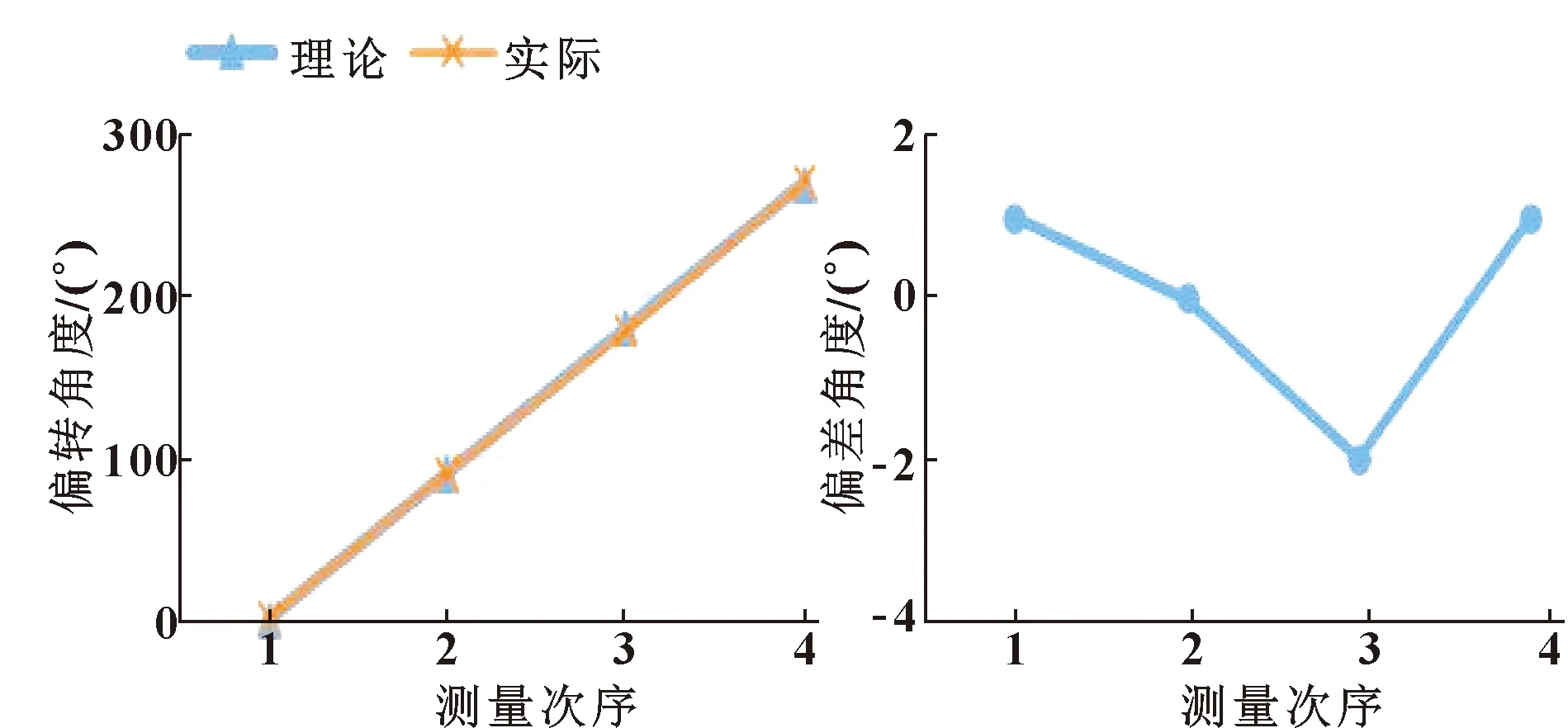
图14 偏转角度 图15 偏转角理论与实际差值
由图14—图15可知:当机器人在空间中以一定弯曲角度做旋转运动时,其旋转角理论值与实际值的偏差较小,不超过2°。这主要是由于运动模型精度和电机的控制精度综合导致的,但对机器人系统整体影响较小,基本实现范围内的角度偏转,符合此系统的设计要求。
3.3 平面弯曲运动实验
所设计的连续体机器人弯曲单元的弯曲角度变化范围为0°~90°,且机器人在各个弯曲平面具有各向同性。故将机器人的偏转角设置为0°进行平面弯曲运动实验,如图16所示,以分析其平面弯曲运动特性。与此同时,通过坐标纸对弯曲运动过程中的弯曲角每间隔10°进行测量,结果如图17所示。
将机器人平面弯曲运动时的弯曲角的理论值与其实际值进行对比分析,结果如图18所示。可知:随着弯曲角的增大,其偏差值也随之增大。这主要是因为绳索拉伸时对柔性弯曲单元造成的弹性变形导致的。驱动绳索拉伸越大,柔性弯曲单元的变形越大,从而影响了弯曲角度。但由于理论角度和实际测量角度成正相关,验证了文中所提运动模型及控制方法的有效性和可行性。
4 总结
针对复杂狭小非结构化环境中的检测需求,本文作者设计了一种新型的一体化加工成型的柔性检测连续体机器人。该结构减少了由于制造和装配误差所引起的机器人控制误差,提高了机器人的控制精度。
在常曲率假设下基于几何分析法建立了柔性连续体机器人的运动学模型,并对其进行运动仿真,验证了弯曲空间到工作空间的正运动学的合理性与准确性。通过绳长变化仿真,阐明了弯曲空间到驱动空间的逆运动学理论。通过控制变量法对位姿进行仿真,验证了运动学建模的正确性。为实现柔性机器人的快速推送运动,所提控制方法采用了仿蛇行运动的控制思想,减少了前行路径与规划路径的偏差,进一步提高了控制精度。
搭建了相应的实验样机并进行验证与分析。结果表明:所提模型和控制方法能够实现机器人的运动控制,且具有较好的控制效果和较高的控制精度。

