基于测地线的移动机器人轨迹规划方法
刘鹏程,张连东,宋雪萍
(大连交通大学机械工程学院,辽宁大连 116028)
0 前言
测地线是欧几里得几何中“直线”概念在黎曼几何中的推广,测地线在黎曼空间中的切矢量方向不改变,是局部最短线[1]。测地线理论在数学、物理学、地质学以及工程技术学领域得到了深入的探究,并于20世纪80年代应用到机器人领域。SHIN和MCKAY[2]在Bendix PACS机器人手臂的关节空间上规划出一条时间最短的测地线路径,实验证明:产生的路径比笛卡尔坐标系下的直线以及联合插值路径消耗的时间要短。BLAKE等[3]在移动机器人手臂上安装一个实时轮廓跟踪器,通过扫描障碍的轮廓,估计出最小路径长度,寻找平滑的最短测地线来绕过障碍物到达目标位置。KIMMEL和SETHIAN[4]在离散化多面体的曲面流形上利用快速推进法获得最短测地线曲线。张连东、王德伦[5]用MATLAB软件解出测地线方程,获得了平面2R机器人在黎曼空间中运动的测地线最短曲线。ORTIZ等[6]在二维环境中,应用测地线规划路径,减少了机器人移动过程中改变方向的次数,产生欧氏空间中的最优化路径。JENA等[7]在位置空间和姿态空间中分别构建黎曼度量,根据不同的初始条件来生成轨迹,依靠3R SCARA机器人的实验数据验证结果是有效的。WU等[8]在三维曲面上非平坦区域,用测地线能量函数的梯度下降法计算出了非线性测地线方程,保证了移动机器人测地线的局部最短路径。HU等[9]结合势场与测地线之间的关系,利用势场构造曲面上的测地线解决了机器人易陷入局部极小值的问题。WU等[10]在原始测地线的基础上,提出了测地线重规划理论,改变了原始测地线易产生边界跟随的缺点,产生的路径符合长度最短的特征,并且算法在MATLAB上实现仿真。
本文作者提出一种通过求解测地线微分方程直接得到移动机器人轮子转角变量的测地线轨迹的方法。以移动机器人的轮子转角为变量,构建机器人轨迹弧长平方的黎曼度量,通过求解该黎曼度量下测地线的微分方程,直接得到机器人轮子转角和角速度表示的移动机器人路径最优的运动轨迹。根据测地线的几何性质,沿着测地线切线方向的速度变化率为0,机器人在沿测地线路径的运动中速度平稳。路径是以轨迹弧长为参考,不受时间约束。求解测地线方程得到测地线的方法,为测地线理论在移动机器人轨迹规划上的实际应用奠定基础。
1 黎曼流形与度量的概念
对于m维欧氏空间Rm来说,设M为Hausdorff空间,有任意一个点x∈M在x的邻域U同胚于Rm的一个开集,则称M是m维流形[1]。假设在流形M上存在对称的二阶协变张量场G,其中(U;ui)是流形的局部坐标图,那么G可以表示为式(1)。
G=gijdui⊗duj
(1)
如果对于任意的X∈Tp(M)都存在G(XX)≥0,并且X=0时G(XX)=0,可以得出G是非退化且正定的。G被称为流形M上的度量张量,因为G是正定的,所以得到M是黎曼流形。黎曼度量的二次微分形式可以表示为式(2),其中ds通常表示弧长元素,gij为黎曼度量矩阵的系数。对于ui=ui(t)在t0≤t≤t1范围内的弧长s可以表示为式(3),其中gij=gji。
ds2=gijduiduj
(2)
(3)
2 构建度量张量求解Christoffel符号
以两轮差分驱动机器人为例,如图1所示差分驱动机器人依靠调节左右轮子独立的轴向运动来实现转弯功能。XI和YI共同组成平面上的全局坐标系,XR和YR构成机器人自身坐标系。为了方便研究机器人在全局坐标系下的运动,通常选取机器人本体上的一个点代替机器人表示其在全局坐标系中的位置。以点P为机器人参考点,点P一般选取两轮差分驱动机器人的两轮轴线中间位置,则机器人的运动学方程表示为
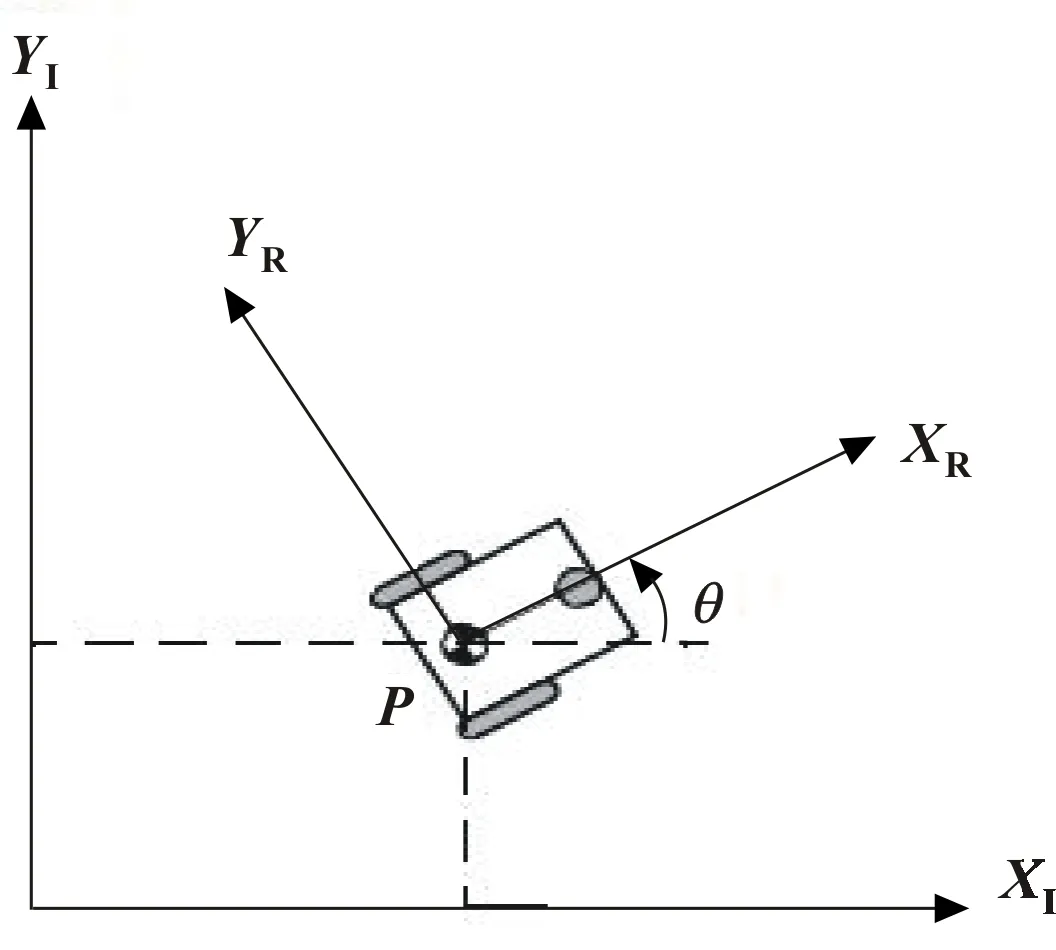
图1 差分驱动机器人运动学模型简图
(4)
其中:r为左右轮子半径;θ为机器人自身坐标系与全局坐标系的夹角;θ1和θ2分别为左、右轮子转角;b为两轮轴向距离。
假设M是二维黎曼流形,在二维黎曼流形上以轨迹弧长微分的平方作为黎曼度量。机器人路径长度的黎曼度量表示为
ds2=dx2+dy2
(5)
式中:ds2为弧长元素的平方值,也就是黎曼度量。
为了构造符合机器人转角参数的黎曼度量,同时满足度量矩阵的正定性质,把运动学方程中的x替换为dx,y替换为dy,θ1和θ2分别用dθ1和dθ2代替,将数值代入黎曼度量表达式(5)中,得到度量为
(6)
将表达式(2)简述为度量矩阵的形式如下:
(7)
得到的黎曼度量矩阵为式(8)。
(8)
矩阵G就是黎曼度量矩阵,因为其正定性求得其逆矩阵G-1为式(9):
(9)
其中gij为G-1的第i行j列的元素。
而表达式:
(10)
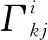
第二类克氏符号由黎曼度量唯一确定,它存在的意义在于:使得在黎曼空间的曲线上始终存在沿着曲线的切矢量在线性移动中保持不变。也就是在平行移动过程中,黎曼度量始终是不变的。克氏符号的唯一性代表了在黎曼流形上存在唯一的无挠容许联络[1]。
SymPy是Python语言中用于代数运算的库,在mpmath库的支持下可以进行任何浮点运算。SymPy作为一种交互式工具,可以在其他程序中自定义函数进行代码的扩展。引用SymPy中的diffgeom函数关于流形、张量计算、第二类Christoffel符号来实现克氏符号分量的求解。在Python语言中习惯从零开始索引,因此在程序中把x0、x1表示为左右轮子的转角θ1、θ2。代码部分如下:
from sympy.diffgeom import Manifold, Patch, CoordSystem
from sympy.diffgeom import TensorProduct as TP
from sympy.diffgeom import metric_to_ Christoffel_2nd as Christoffel
from sympy import symbols
r,b = symbols("r,b")
n = 2
M = Manifold(′M′, n)
P = Patch(′P′, M)
coord =CoordSystem(′coord′, P, [′x%s′%i for i in range(n)])
x = coord.coord_functions()
dx = coord.base_oneforms()
g=[[(r**2/4)*(1+(x[0]+x[1])**2*(r**2/b**2)),(r**2/4)*(1-(x[0]+x[1])**2*(r**2/b**2))],[(r**2/4)*(1-(x[0]+x[1])**2*(r**2/b**2)),(r**2/4)*(1+(x[0]+x[1])**2*(r**2/b**2))]]
metric=0.5*sum([g[i][j]*TP(dx[i],dx[j]) for i in range(n) for j in range(n)])
C = Christoffel(metric)
利用程序获得的克氏符号分量为式(11)
(11)
3 测地线方程的求解
对于移动机器人而言,轮子的转角是机器人轨迹曲线的重要组成参数。在测地线理论中,假设n维空间中的曲线C:θi=θi(t)符合沿曲线切向量的协变微分是0,即曲线切方向的速度保持不变,那么这条曲线就符合测地线理论,曲线C就是所求的测地线。这时选取弧长s作为曲线C的主要参数,其dθi/ds为它的切向量分量,得到曲线切向量的协变微分:
(12)
令式(12)中的D(dθi/ds)为0,可以得到测地线方程的一般形式为
(13)
式中:i、j、k循环取遍1、2。
将测地线方程展开为如下两个等式:
(14)
把程序求得的克氏符号分量代入式(14)中得到式(15)
(15)
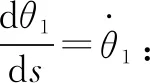
(16)
下面用SciPy库中的odeint函数实现式(16)的求解。SciPy库包含很多科学计算以及工程上应用公式的求解,使用SciPy库通常进行微分方程的求解、信号函数的分析等。通常为了图形化数据,结合matplotlib生成二维或者三维的图形,观察输出的图形与想要得到的结果是否相同。为了使输出结果更直观,假设机器人左右轮子半径r为单位长度1,并且机器人两轮之间的轴向距离b也为单位长度1。引入Scipy库中的odeint函数,将式(16)中的微分方程封装到geodesic函数中,部分代码如下:
from scipy.integrate import odeint
def geodesic(w,s,v):
x0, y0, x1, y1 = w
r,b=v
f=[y0,-(2*(b**2)-r**2*((x0+x1)**2))/(2*(b**2)*(x0+x1))*(y0**2)-(x0+x1)*(r**2)/(b**2)*(y0*y1)+(2*(b**2)+r**2*(x0+x1)**2)/(2*(b**2)*(x0+x1))*(y1**2),y1,(2*(b**2)+(r**2)*((x0+x1)**2))/(2*(b**2)*(x0+x1))*(y0**2)-(x0+x1)*(r**2)/(b**2)*(y0*y1)-(2*(b**2)-r**2*(x0+x1)**2)/(2*(b**2)*(x0+x1))*(y1**2)]
return f
按照之前定义好的的半径与轮子轴向距离,将情况A中的的参数数值代入函数中:
r=1,b=1,x0=1.795,y0=1,x1=0.295,y1=1
v=[r,b]
w0=[x0,y0,x1,y1]
取终止长度为2,样本点为500:
stoplength = 2
numpoints = 500
s = [stoplength * float(i) / (numpoints - 1)for i in range(numpoints)]
调用odeint()函数,设置相应的参数求解微分方程:
wsol=odeint(geodesic,w0,s,args=(v,),atol=1.0e-10, rtol=1.0e-8)
算法流程如下:
(1)定义以转角为参数的差分驱动机器人测地线方程,将一阶微分方程定义到函数之中。
(2)根据不同的运动状态定义初始条件。
(3)设置ode求解器适当的参数。
(4) 为ode求解器输出创建曲线长度样本。
(5)调用ode求解器实现测地线方程的求解。
(6)用matplotlib输出曲线图像。
差分驱动机器人的初始位姿与由角速度引起的机器人轨迹的变化是不相关的,也就是说差分驱动机器人按照固定的角度与角速度运动,所产生的内在轨迹是不变的,只不过机器人自身坐标系相对世界坐标系转角发生变化。因此为了方便计算,假设机器人的初始位置在世界坐标系的原点,取弧长范围是0~2,样本点为500个。初始化不同角速度如下:
将A、B、C所列出的不同角速度与角加速度分别代入公式(16)中,得到不同初始条件的图像,如图2—图4所示。
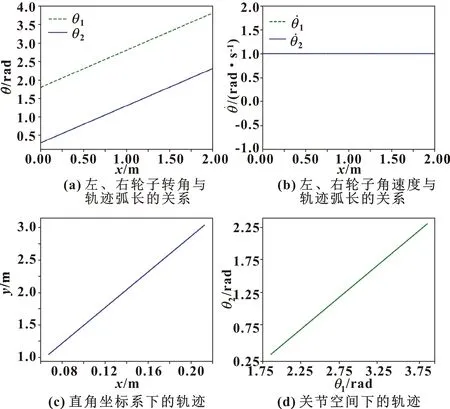
图2 初始条件A中轮子转角以及其角速度的轨迹

图3 初始条件B中轮子转角以及其角速度的轨迹
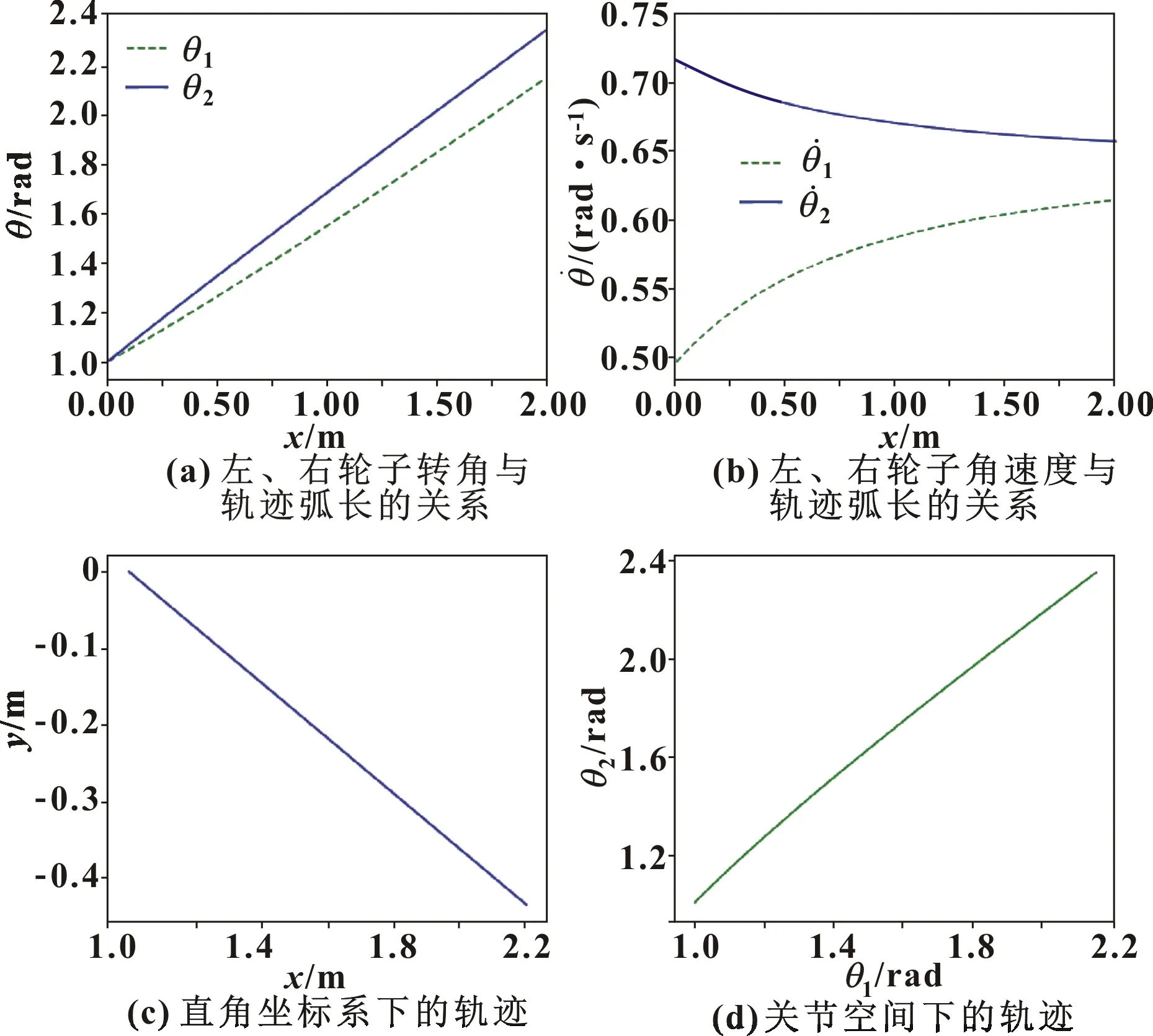
图4 初始条件C中轮子转角以及其角速度的轨迹
情况A中,图2(a)表示在弧长递增的情况下左、右轮子角度与弧长的关系,可以看出角度分别从各自的初始角度逐渐增加,并且增速基本相同,这也就意味着机器人在环境中是前进的。由于给定的两轮初始角速度是相等的,通过图2(b)可知,角速度与轨迹弧长关系的曲线重合。在弧长递增的情况下,由测地线微分方程得到的机器人左、右轮子的角速度轨迹是相同的且保持相对的稳定。图2(d)表示关节空间中的测地线轨迹,因为初始角速度是相同的,所以轨迹是一条斜直线。
情况B中,因为左右轮子不同的角速度以及不同的起始角度,图3(a)中的轨迹形状与图2是不同的。左轮转角与弧长关系曲线在右轮上方,这是因为初始角度之间存在差异。按照图像曲线的走势,可以看到随着弧长的增加,左、右轮子转角越来越接近。对于图3(b),右轮的角速度比左轮大,呈现出来的轨迹是上凸的曲线,这符合机器人的运动学模型。情况C中,左右轮子的角速度差值不如情况B,可以从图4(d)中看出曲线上凸不是很明显,这也就进一步证明与机器人运动是相符的。
根据测地线理论,由测地线方程求解出来的测地线在欧氏空间是最短线。针对3种情况中生成的轨迹,如图2(c)、图3(c)、图4(c)所示,生成的轨迹为直线,也就是欧氏空间中的最短线。并且根据机器人运动方程把初始转角代入其中,得到的初始机器人自身坐标系与世界坐标系的夹角θ与欧氏空间中直线与x轴的夹角是一致的。由此得到,由测地线方程求解直接生成的测地线是局部的最短线。
4 结论
首先建立了两轮差分移动机器人的数学模型,在此数学模型的基础上,构建了移动机器人的运动轨迹弧长平方的运动学黎曼度量。该黎曼度量下的测地线方程是机器人运动的最短路径。在给定的黎曼度量下,测地线由初始条件唯一确定。传统的移动机器人轨迹规划主要是利用各种优化算法得到机器人的最优轨迹,然后转化为机器人电机的控制变量,控制机器人沿着规划好的轨迹运动。而基于测地线的轨迹规划方法是根据不同的优化目标得到的黎曼度量,直接得到关节(移动机器人轮子电机)空间内的测地线最优轨迹,对机器人进行控制。另外,传统的移动移动机器人控制变量是基于时间参考的,当机器人遇到未知障碍受阻后,原来的规划可能会失效。而测地线轨迹规划是基于路径弧长为参考的,当障碍物被移除后,机器人可以按照原有的非时间参考的轨迹规划继续运动。
通过Python语言,针对不同的初始条件求出了相应的测地线方程,实现了测地线方程ROS环境下的求解,轨迹仿真结果验证了测地线轨迹规划方法的正确性,为测地线实时轨迹规划与ROS系统实时控制的集成奠定了基础。

