平面状态对疲劳裂纹数值扩展的影响研究

徐康宾，杨亚莉

（201620 上海市 上海工程技术大学 机械与汽车工程学院）

0 引言

工程构件在生产、安装、使用过程中难免会受到挤压、划伤等，造成表面损伤，在循环荷载作用下，这些表面损伤将演变为表面裂纹，最终引发断裂，从而导致构件失效。因此，研究表面裂纹的扩展机理具有很大的经济价值和现实意义[1-4]。

在表面裂纹扩展研究中，数值方法由于低成本、高精度受到广泛应用。Newman[5]、Song[6]和Liu[7]提出了裂纹前缘形状为椭圆、表面点和深度点独立扩展的假设。Lin 和Smith[8]提出了一种沿裂纹前沿9 个点预测形状变化的技术。Toribio[9-10]等认为裂纹前沿为椭圆，将椭圆分为14 个部分，采用最小二乘法确定裂纹前沿的形状。

上述学者对疲劳裂纹数值扩展的研究中都把扩展点状态统一看作平面应变状态，没有考虑到最外侧的扩展点其实是应力状态的情况。

因此，本文首先基于平面内任意位置的平面状态是平面应力状态与平面应变状态的组合状态的假设，用权重系数来表示平面应变状态在该位置所占的比重，并将权重系数用于平面内任意位置的应力强度因子表达式；提出了相对深度系数的概念，并假设了3 种权重系数与相对深度系数的关系；最后，基于这3 种关系进行疲劳裂纹数值扩展，利用数值结果处理方法得到3 种关系下的数值结果精度，并与其他文献进行了对比。

1 J 积分计算

首先在ABAQUS 软件中计算出所有积分点的J积分，步骤如下：

（1）在Part 模块中建立圆柱体模型，圆柱体直径为12，长度为90；

（2）在Property 模块中赋予部件材料属性，弹性模量为206 000，泊松比为0.33；

（3）在Assembly 模块中建立装配体，装配方式选择独立装配；

（4）在Step 模块中建立分析步，类型为静态通用类型；

（5）在Part 模块中进行圆柱体分割并在分割面上绘制裂纹线。利用圆柱体中截面将圆柱体一分为二，根据相应的参数完成在中截面上绘制椭圆弧；

（6）在Interaction 模块中创建裂纹。先在中截面上指派裂纹区域，然后再创建裂纹，创建裂纹类型为环线积分；

（7）在Step 模块中修改历史输出。在历史输出中选择裂纹，输出类型为J 积分，积分次数为10；

（8）在Load 模块中施加载荷与约束。在圆柱体一端施加全固定约束，另一端施加100 MPa 拉力；

（9）在Mesh 模块中进行网格划分，设置裂纹线上的种子数为80，从而可在裂纹上得到81 个积分点，然后调整其它部分的种子数，以便完全产生六面体网格；

（10）在Job 模块提交计算，计算完成后在工作目录里会有dat 和inp 文件。

用记事本打开inp 文件，可查找到81 个积分点的节点编号和坐标，用记事本打开dat 文件进行查找，可得81 个积分点的J 积分。

对于某一个扩展点，首先找出与其最接近的2 个积分点p1和p2，然后计算扩展点到积分点的距离L1和L2。

式中：xp，yp——扩展点p 的坐标；xp1，yp1——积分点p1的坐标，xp2，yp2——积分点p2的坐标。

最后，根据距离求出扩展点p 的J 积分值Jp。

式中：Jp1——积分点p1的J 积分值；Jp2——积分点p2的J 积分值。

3 应力强度因子的计算

当得到某到扩展点对应的J 积分后，即可求出该扩展点的应力强度因子，计算公式为：

考虑到扩展面上的任意一个扩展点大都不是完全的平面应力状态或平面应变状态，而是两种平面状态的混合体，不同的是2 种状态所占的比重不同，基于这个假设，本文提出了一个新的应力强度因子计算公式，其表达式为：

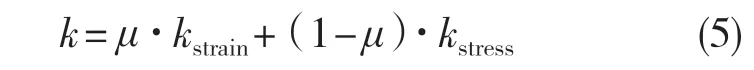
式中：μ——平面应变状态所占的权重系数。

另外，对于每一个扩展点，其坐标 假设为（x0，y0），提出了一个扩展点相对深度λ的概念，λ的意义为到圆柱体表面的相对距离，λ越大表明扩展点距离圆柱体表面越远。其定义公式为：

式中：Xc，Yc——圆心的横坐标与纵坐标；D——圆柱体直径。

显然，当λ=0 时，扩展点位于圆柱体表面，则k 应当为kstress，也即说权重系数μ应当为0。当λ=1 时，扩展点位于圆柱体中心，则k 应当为kstrain，也即说权重系数μ应当为1。

基于上述关系，不妨假设μ与λ存在以下几种关系：

又由于当λ分别为0 和1 时，μ也分别为0 和1，因此可以求解出μ与λ的具体关系式：

联立式（4）、式（5）、式（8），可以得到应力强度因子的表达式为：

3 裂纹扩展方法

首先确定第i 条裂纹扩展到第i+1条裂纹的步骤。

（1）给出第i 条裂纹的坐标方程，如式（10）所示。其中和都是已知的。

（2）确定在第i 条裂纹上的5 个扩展点（x（i，j），y（i，j））。

（3）给出第i+1 条裂纹的坐标方程，如式（11）所示。其中给定，为任意值。

（4）在2 条裂纹之间创建扩展圆。由于这些圆与前后2 条裂纹相切，且切点为扩展点，从而可以确定第i+1 条裂纹上的扩展点（x（i+1，j），y（i+1，j））。

（5）依据公式（12）计算每个扩展点对应的等效应力强度因子Δkej。

式中：k（i，j）——第i+1 条裂纹上第j 扩展点的应力强度因子；k（i+1，j）——第i+1 条裂纹上第j 个扩展点的应力强度因子；j——扩展点编号，j=1，2，…，5。

（6）给定第1 个扩展点的扩展量，从而根据式（13）确定其他扩展点的扩展量。

式中：ΔL1——第1 个扩展点的扩展量；Δke1——第1 个扩展点对应的等效应力强度因子。

（7）根据扩展点沿着垂直于第i 条裂纹前进ΔLj/2 可得扩展圆心的坐标（x（c,j），y（c,j））。

（8）根据式（14）计算扩展圆心与第i+1 条裂纹上的扩展点的距离：

（9）根据式（15）计算当前参数下第i+1 条裂纹的误差：

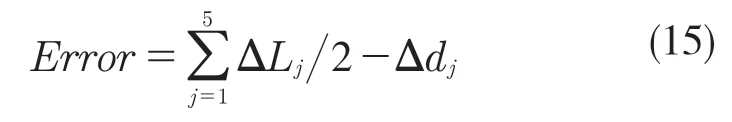
当i=1 时，裂纹为初始裂纹，是已知的，从而可以得到第2 条裂纹，以此类推，可得到所有裂纹。

4 数值结果处理

由于有3 组裂纹扩展的数值结果，因此需要计算每一组数值结果的预测精度。方法是先将每一组数值结果与实验结果的误差进行量化，之后取其倒数作为每组数值结果的预测精度。其中，实验结果来源于文献[11]。

4.1 实验结果的处理

图1 是用Origin 软件拟合实验数据后的结果图，图1 中的拟合结果如表1 所示。则实验数据拟合曲线的方程为

图1 实验结果拟合图Fig.1 Fitting diagram of experimental results

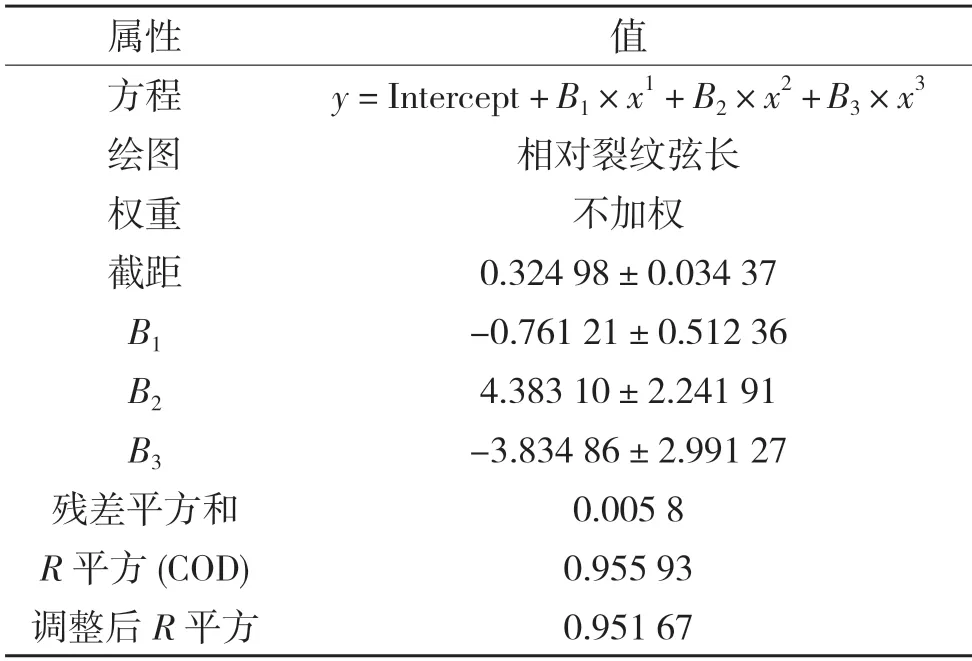
表1 实验数据拟合结果Tab.1 Experimental data fitting results

4.2 仿真结果与实验结果的误差计算

将实验数据拟合后，实验结果可以用一条曲线代替。而数值结果也能用一条曲线表示，因此可以将数值结果与实验结果的误差用两条曲线的误差代替，示意图如图2 所示，具体步骤如下：

图2 曲线误差示意图Fig.2 Schematic diagram of curve error

（1）将数值结果中的n 个数据点连接起来。

（2）在实验拟合曲线中取出n 个数据点，保证两条曲线中的n 个数据点的相对裂纹深度相同。

（3）计算两条曲线中n 个数据点的相对裂纹弦长差Δyi。

（4）计算两条曲线的误差。

5 结果与讨论

表2、表3 和表4 分别是3 种关系下的裂纹扩展数值结果。表5 是Yang 等[12]基于扩展点为平面应变状态得到的数值扩展结果。将上述4 组数值结果处理后可得到相应的数值结果误差，如表6 所示。

表2 线性关系下的裂纹扩展数值结果Tab.2 Numerical results of crack propagation under linear relationship

表3 指数关系下的裂纹扩展数值结果Tab.3 Numerical results of crack growth under exponential relationship

表4 二次函数关系下的裂纹扩展数值结果Tab.4 Numerical results of crack propagation under quadratic function relation

表5 Yang 等人的裂纹扩展数值误差Tab.5 Numerical error of crack propagation by Yang,et al

表6 各组数值结果精度Tab.6 Precision of numerical results for each group

从表6 可以看出，基于本文提出的3 种关系而得到的数值结果精度明显高于Yang 等人的数值结果精度。在本文的3 组数值结果精度中，基于二次函数关系而得到的数值结果精度最高，基于指数函数关系而得到的数值结果次之，基于指数函数关系而得到的数值结果最低。

结果表明，相对于把扩展点的平面状态看作是平面应变状态，把它看作是平面应变状态与平面应力状态的组合状态更能提高数值扩展的精度。而在3 种关系对应的组合状态中，二次函数关系是最能提高数值扩展精度的关系。

6 结论

本文研究了平面状态对疲劳裂纹数值扩展的影响。具体的结论如下：

（1）利用ABAQUS 软件求解了所有积分点的J 积分，并根据扩展点到积分点的距离求出扩展点的J 积分值；

（2）基于平面状态是平面应力状态和平面应变状态的组合状态的假设，利用权重系数代表平面应变状态所占的比重，并将其用于应力强度因子的表达式，然后，提出了相对深度系数的概念，并假设，权重系数与相对深度系数分别呈线性、指数和二次函数关系；

（3）基于权重函数与相对裂纹深度的3 种关系，通过裂纹扩展方法进行数值扩展，得到3 种关系下的疲劳裂纹数值结果。利用本文中提出的数值结果处理方法得到3 种关系下的数值结果精度；

（4）通过对数值结果的分析表明，将平面状态看作是平面应力状态与平面应变状态有助于提高数值扩展的精度，并且当权重系数与相对深度系数的关系为二次函数时数值扩展精度最高。