双馈交替极磁通反向电机极槽配合研究
窦永亮,杨自栋,郑语婷
(1.311300 浙江省 杭州市 浙江农林大学;2.310027 浙江省 杭州市 浙江科技学院)
0 引言
随着《中国制造2025》的提出,高效节能成为我国工业生产发展的方向,电机作为生产中的动力设备被广泛应用[1-2]。定子上有永磁体(PM)的电机被称为定子永磁电机,由于它们克服了转子永磁电机散热差和退磁风险大的问题,因此在过去的几十年中受到了相当大的关注[3-5]。根据永磁体的位置,定子永磁电机主要可分为3 类:永磁体插入定子齿中的磁通切换永磁(FSPM)电机[6-7],永磁体插入定子轭中的双凸极电机[8],永磁体安装在定子齿表面上的磁通反向电机(FRM)[9-10]。其中FRMs 在低速大转矩应用中引起相当大的关注[11]。
传统FRM 的转矩性能由于其固有的较大等效气隙长度以及绕组和PM 之间的空间冲突而受到限制。为了提高转矩密度,许多新式的FRM 结构被提出,包括但不限于使用铁芯作为另一个磁极的交替极结构[12-13],在每个定子齿的表面上安装多块磁铁[14-15],在定子内表面上放置均匀分布的PM[16],或在定子槽开口中使用halbach 阵列磁铁[17]。上述研究与传统FRM相比实现了不同程度的转矩提升,但绕组和PM 之间的空间冲突问题依然存在,制约了转矩密度的进一步增长。
最近,一种新型双馈(DF)FRPM (DF-FRPM)电机被提出。该电机在定子和转子槽中放置有两组独立的电枢绕组,其谐波分析也在得到了详尽的研究。DF-FRPM 从根本上解决了绕组和PM 之间的空间冲突,实现了极大的转矩提升。基于2 组电枢绕组的概念,提出了一个12 定子槽/14 转子槽DF 交替极(CP)FRM(DF-CPFRM),并对其电磁性能进行研究,与传统的CPFRM 进行了比较。然而定子和转子的极槽配合没有被上述研究考虑在内,它会影响优化过程中的关键参数选择,更重要的是,它会对DF-CPFRM 的电磁性能产生影响。
本文将对DF-CPFRM 的极槽配合进行研究,对5 个具有不同极槽配合的DF-CPFRM 和一个传统CPFRM 进行优化,并基于有限元(FE)方法比较它们的电磁性能,然后制造一个样机来验证上述有限元分析。
1 电机拓扑结构和优化
图1(a)展示了只在定子槽中有电枢绕组的传统12 定子槽/14 转子槽 CPFRM 结构,图1(b)—图1(f)展示了5 个具有不同极槽配合的DF-CPFRM 结构,即定子极数为12,而转子极数分别为10、11、13、14 和16。需要说明的是,6台电机的定子相数均为3,而10、11、13、14、16转子槽的DF-CPFRM 的转子相数分别为5、11、13、7 和4。它们的定子与转子绕组分相情况也展示在图1 中。应该注意的是,转子相数的增加有利于提高电机的容错能力,但也会导致需要更多的电力电子器件[18],因此需要在容错能力和成本之间权衡。


图1 CPFRM 和DF-CPFRFM 结构图Fig.1 CPFRM and DF-CPFRFM configurations
在本节中,前面提到的CPFRM 和5 个DFCPFRM 都以转矩最大为目标进行了优化。研究定子和转子的极槽配合对优化过程中关键参数选择的影响。为了保证性能对比的公平性,所有电机均采用相同的定子外径、轴向长度和总铜损(32 W)。
1.1 裂比
裂比是一个关键参数,它对这些具有不同极槽配合的DF-CPFRM的平均转矩的影响如图2所示。很明显,所有电机都具有相同的转矩变化趋势,并且与传统的CPFRM 相比,整体上DF-CPFRM 具有更高的转矩。10、11、13 转子槽的DF-CPFRM 在裂比为0.7 时转矩最大,而14、16 转子槽的DFCPFRM 在裂比达到0.72 时转矩最大,因为后者具有更多的转子齿,需要更多的转子电枢绕组空间。
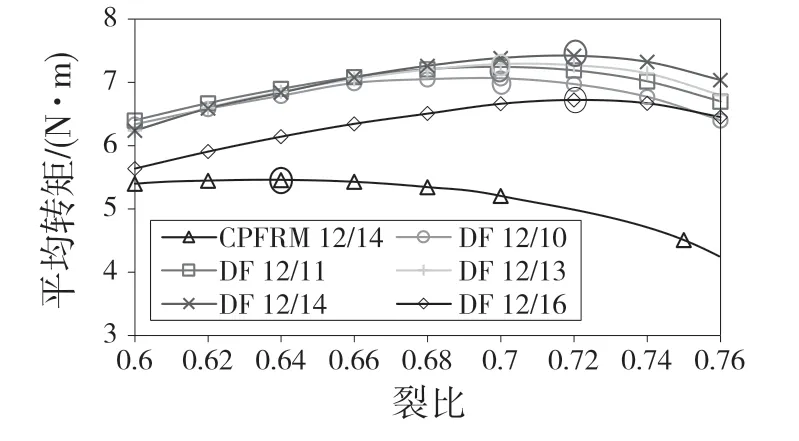
图2 裂比对转矩的影响Fig.2 Torque variation against split ratio
1.2 定子槽口比
定子槽口比,即定子槽口宽度与定子极距之比,对平均转矩的影响如图3 所示。与传统的CPFRM 相比,DF-CPFRM 具有更小的最优定子槽口比,因为较小的定子槽口会导致较大的PM 体积,有利于转子转矩的产生。10 转子槽的DF-CPFRM的最优定子槽口比为0.05,而16 转子槽的DFCPFRM 在定子槽口比为0.15 时获得最大转矩。

图3 定子槽口比对转矩的影响Fig.3 Torque variation against stator slot opening ratio
1.3 转子槽口比
图4 展示了平均转矩相对于转子槽口比的变化,即转子槽开口宽度与转子极距的比值。所有电机都表现出相同的变化趋势,转矩先增大然后减小。这是因为较大的转子槽口减少了漏磁,导致转矩增大,但当转子槽口过大时,会削弱转子齿的调制作用,导致转矩降低。10、11、13 转子槽的DF-CPFRM 的最优转子槽口比为0.75,而14、16转子槽的DF-CPFRM 的最优转子槽口比为0.7。因为后两种电机的转子齿宽较窄,在这些情况下,较小的转子槽口比有利于转子齿的调制效果。

图4 转子槽口比对转矩的影响Fig.4 Torque variation against rotor slot opening ratio
1.4 永磁体厚度和永磁体比
PM 至关重要的尺寸包括厚度和比,它们对转矩性能的影响如图5 和图6 所示。PM 厚度涉及永磁磁通和等效气隙长度。更大的PM 厚度会导致更高的永磁磁通,但也会导致更大的等效气隙长度,因此在这两个因素之间存在折衷,并且存在最优PM 厚度。可以观察到,当PM 厚度为3 mm 时,所有电机都获得最大的转矩。

图5 PM 厚度对转矩的影响Fig.5 Torque variation against magnet thickness

图6 PM 比对转矩的影响Fig.6 Torque variation against magnet ratio
PM 比定义为PM 宽与定子齿宽之比。图6 展示了平均转矩随PM 比的变化。可以发现,无论极槽配合如何,所有电机都表现出相同的趋势和相同的最优PM 比。当PM 比为0.5 时,即PM 宽度等于铁磁极靴宽度时,所有电机都获得最大的转矩。
2 性能对比
在全局优化后,本节研究和比较了具有上述极槽配合的CPFRM 和DF-CPFRM 的电磁性能,包括反电动势、转矩性能、损耗和效率。所有电机优化后的关键参数如表1 所示。

表1 CPFRM 和 DF-CPFRM 优化后的关键参数表Tab.1 Main parameters of optimized CPFRM and DF-CPFRMS
CPFRM 和DF-CPFRMs 的定子相反电动势频谱如图7 所示。可以观察到,11 和13 转子槽的DF-CPFRMs 只有奇次谐波,而其他的同时表现出奇次谐波和偶次谐波,此外,随着转子齿数的增加,定子相反电动势的幅值也增加,但具有16 转子槽的DF-CPFRM 的定子相反电动势幅度值在所有DF-CPFRM 中最低,这主要是因为绕组因数小。
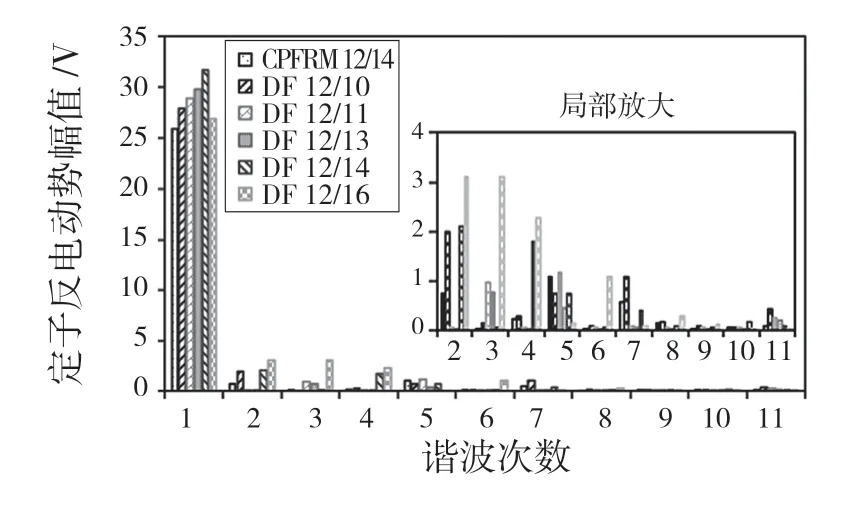
图7 CPFRM 和 DF-CPFRMs 的定子相反电动势频谱图Fig.7 Stator back-EMF spectra of CPFRM and DF-CPFRMs
图8 展示了具有不同极槽配合的DF-CPFRM的转子相反电动势频谱。可以看出,所有DFCPFRM 的转子相反电动势都表现出较大的3 次谐波,这将导致转子相数为4 的16 转子槽的DFCPFRM 产生转矩脉动。但具有10、11、13 和14转子槽的DF-CPFRM 不会产生转矩脉动,因为它们的转子相数分别为5、11、13 和7。具有16 转子槽的DF-CPFRM 具有最低的幅值,这是由于较低的绕组因数和减弱的调制效应。

图8 CPFRM 和 DF-CPFRMs 的转子相反电动势频谱图Fig.8 Rotor back-EMF spectra of CPFRM and DF-CPFRMs
CPFRM 和DF-CPFRM 的齿槽转矩峰值和平均转矩性能见表2。显然,与传统的CPFRM 机相比,所有极槽配合的DF-CPFRM 都表现出更大的平均转矩。其中,11 转子槽的DFCPFRM 平均转矩最大,14 转子槽的DFCPFRM 齿槽转矩最小。可以发现,当定子槽数接近转子槽数时,即12 定子槽DF-CPFRM 带有11 或13 转子槽时,可以获得较大的平均转矩。

表2 CPFRM 和DF-CPFRM 的转矩性能Tab.2 Torque performance of CPFRM and DF-CPFRMS
CPFRM 和DF-CPFRM 的过载能力对比见图9。可以看出,当电负荷较低时,11、13、14 转子槽的DF-CPFRM 均具有较大转矩能力,而14 转子槽的DF-CPFRM在高电负荷下表现出最大平均转矩。

图9 CPFRM 和DF-CPFRM 转矩与铜耗特性图Fig.9 Torque versus copper loss characteristics of CPFRM and DF-CPFRMs
表3 给出了CPFRM 和DF-CPFRM 的损耗和效率比较。可见,与铜损相比,铁损相对较小。所有DF-CPFRM 由于输出功率较大,表现出比传统CPFRM 更高的效率。在5 种不同极槽配合的DFCPFRM 中,11 转子槽的DF-CPFRM 铁损最小,输出功率最大,效率最高。
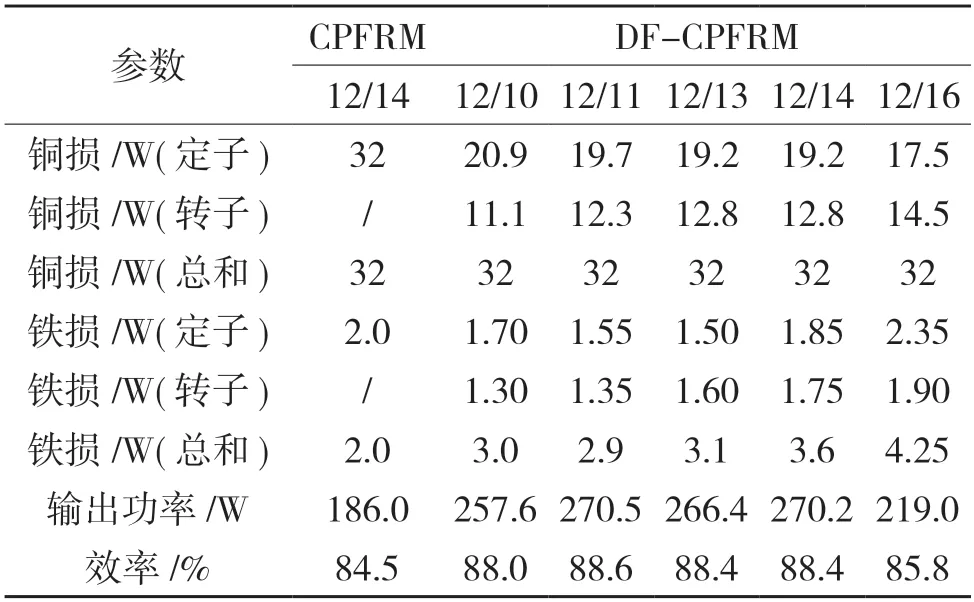
表3 CPFRM 和DF-CPFRM 的损耗和效率表Tab.2 Loss and efficiency of CPFRM and DF-CPFRMS
3 实验
制作了12 定子槽/14 转子槽DF-CPFRM 样机并进行实验,以验证前面的FE 分析。图10 给出了12 定子槽/14 转子槽样机的照片,包括叠片、定子、转子、滑环和整机。

图10 12 定子槽/ 14 转子槽DF-CPFRM 样机Fig.10 12-stator-slot/14-rotor-slot DF-CPFRM prototype
样机的齿槽转矩可采用文献[12]介绍的简单方法测量。有限元预测和实测的齿槽转矩波形的比较如图11 所示,可以观察到良好的一致性,它们之间的不匹配主要是由制造公差引起。

图11 有限元预测和实测的齿槽转矩波形Fig.11 FE predicted and tested cogging torque waveforms
图12 对比了样机在300 r/min 时的FE 预测和实测反电动势波形,包括定、转子相反电动势。可见,反电动势基波实测值略小于FE 预测值,主要是由于忽略了端部效应。总的来说,实验结果与有限元结果吻合较好。
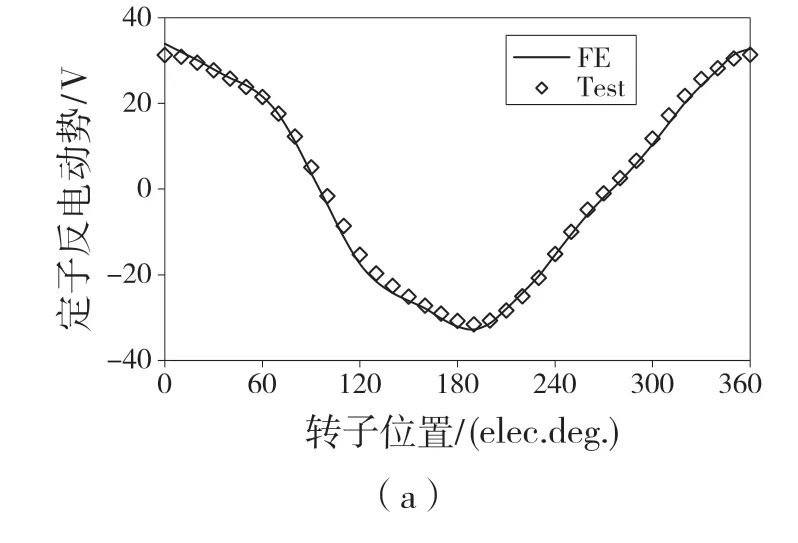

图12 有限元预测和实测的反电动势波形Fig.12 FE predicted and tested back EMF waveforms
通过供给三相定子电枢绕组和的七相转子电枢绕组直流电流,即可测量样机的定转子静态转矩。FE 预测与实验静态转矩波形对比见图13。可见实测定转子静态力矩与其FE 预测结果吻合较好。

图13 有限元预测和实测的静态转矩波形Fig.13 FE predicted and tested static torque waveforms
4 结论
本文研究了定转子极槽配合对DF-CPFRM 的优化和电磁性能的影响。优化结果表明,具有较多转子齿的DF-CPFRM 具有较大的裂比和较小的转子槽口比。此外发现,当定子槽数接近转子槽数时,绕组因数较大,可获得较高的平均转矩。在5 种极槽配合的DF-CPFRM 中,11 转子槽的DF -CPFRM 具有最高平均转矩和效率,而14 转子槽的DF -CPFRM 在高电负荷下具有最好的过载能力。

