改进灰狼算法提高数字光刻图像质量的研究
杨成,刘红,王英志,胡俊
(1.长春理工大学 光电工程学院,长春 130022;2.长春理工大学 电子信息工程学院,长春 130022)
在光刻投影成像过程中,存在光学邻近效应,光刻图形会发生畸变,特别是当特征尺寸接近系统理论分辨率极限时,图像失真更为严重,最终影响光刻产品的质量[1]。学者们提出了许多方法来解决这一问题,其中数字光刻技术和光学邻近校正技术逐渐被大多数科研人员所认可。
光学邻近校正[2]原理是通过改变掩模的结构,比如在原始掩模中添加衬线、散射条等方式提高光刻分辨率,该技术缺点是优化自由度较低,精度不高。数字光刻技术[3]利用各类算法优化光源和掩模的结构(SMO)来提高光刻成像质量。SHEN[4]提出了一种距离水平集正则化的SMO重拟方法,该方法以更简单、更有效的数值实现保证,提高了计算效率。DMD具有反射效率高、分辨率高、对比度高、稳定性好,刷新速度快等优点[5]。分析DMD的结构可知,数字掩模是通过操控DMD每个微镜的开关来生成的。因此,如何控制DMD微镜阵列的偏转优化掩模图形从而改善DMD光刻成像质量是一个非常重要的问题。其中王磊等人[6]提出的基于粒子群算法的掩模优化技术,可以随意选择优化目标与光刻成像模型,适应性很强。然而,粒子群算法虽然简单易于实现,但是其寻优精度低且收敛速度慢[7-8]。
灰狼优化算法相较于粒子群算法编程难度更小,并且灰狼优化算法本身并不依赖于参数的设置,而粒子群算法在搜索性能方面过分依赖于调制参数[9],因此灰狼优化算法的全局搜索能力比粒子群算法更强,优化速度也较之为粒子群算法更快。但是灰狼优化算法在解决复杂优化问题时仍然存在易陷入局部极值,即早熟收敛的现象[10]。
提出了一种基于改进灰狼优化算法的数字光刻掩模优化方法。将数字掩模解析为灰狼个体,评价函数设置为原始数字掩模与优化后数字掩模的图形误差(PE),不断迭代优化掩模中每个像素的灰度值,最终实现数字光刻图形质量改善的目的。
1 光刻成像模型
在数字光刻中,通过计算机模拟技术来分析基于DMD的数字光刻成像过程是必不可少的。在Kang等人[11]提出的基于像素的立体光刻技术中,利用数学模型来描述单个像素的光强分布,并计算能量估计光刻图形。单个像素的光强分布可以看作是一个点扩散函数,可以由高斯分布描述为一阶近似。为了构建数学模型,建立了单个像素的全局坐标与局部坐标如图1所示。
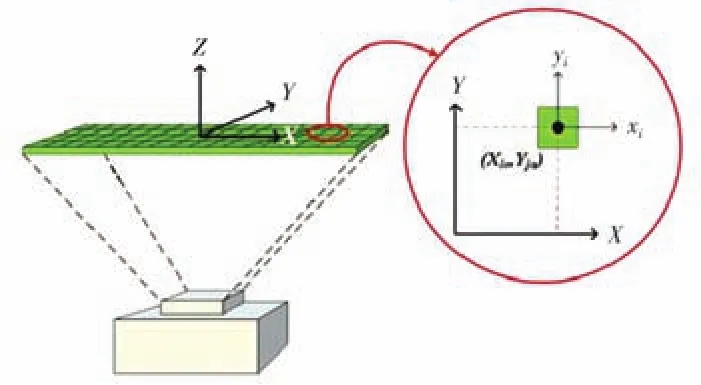
图1 数字掩模单个像素全局和局部的笛卡尔坐标
基于这两个坐标系统,单个像素的光强分布可以表示为:
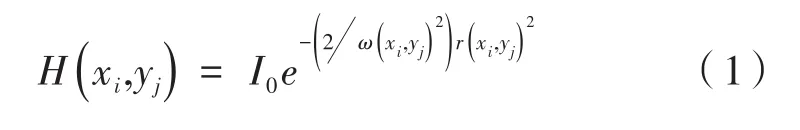
其中,H(xi,yj)为点(xi,yj)的光强;I0为单个像素的峰值强度;r(xi,yj)为一个像素的中心到点(xi,yj)的距离;ω(xi,yj)为沿着点(xi,yj)方向1/e2的高斯半宽度光强分布。
此外,r(xi,yj),ω(xi,yj)和点(X,Y)的光强I(X,Y)可以表示为:
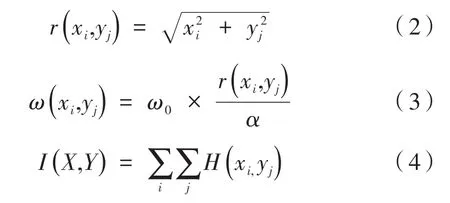
其中,ω0为沿着xi或者yj方向的1/e2高斯半宽度光强分布,如果,α=xi如果
假设p为两个相邻像素间的距离,那么xi和yj可以表示为:
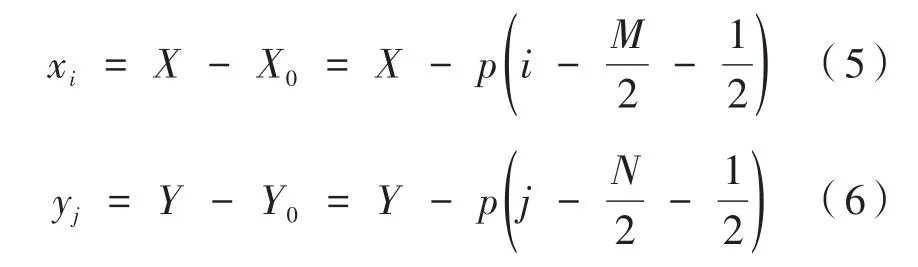
其中,i=1,2,3,…,M,j=1,2,3,…,N。
2 灰狼优化算法改进原理
2.1 原始灰狼优化算法
Mirjalil经过长期观察灰狼群体协作狩猎,在2014年提出了灰狼优化算法[12]。灰狼群体的狩猎过程分为追踪、包围以及进攻三个阶段。
在GWO算法中,将前三个最优解依次记为α,β,δ,其余灰狼个体全部记为ω。在狩猎过程中,灰狼团体首先会对猎物进行包围,用数学公式可以表示如下:
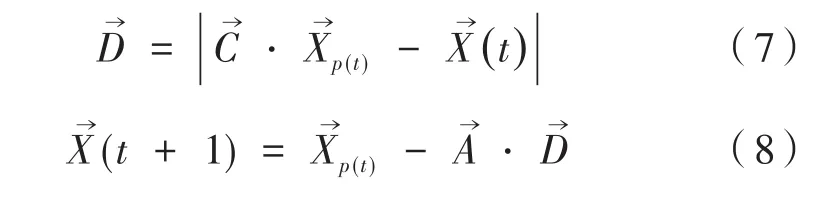
式中,t表示迭代次数;表示灰狼与猎物之间的距离;表示猎物的位置 ;表示灰狼的位置;和表示向量系数。其计算公式如下:
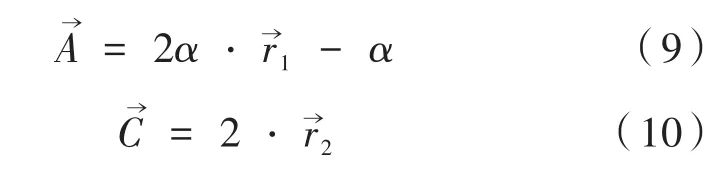
其中,α随着迭代次数依次从2递减为0,。
经过包围阶段,灰狼团体对猎物发起进攻,此时,灰狼个体的位置也发生了更新:
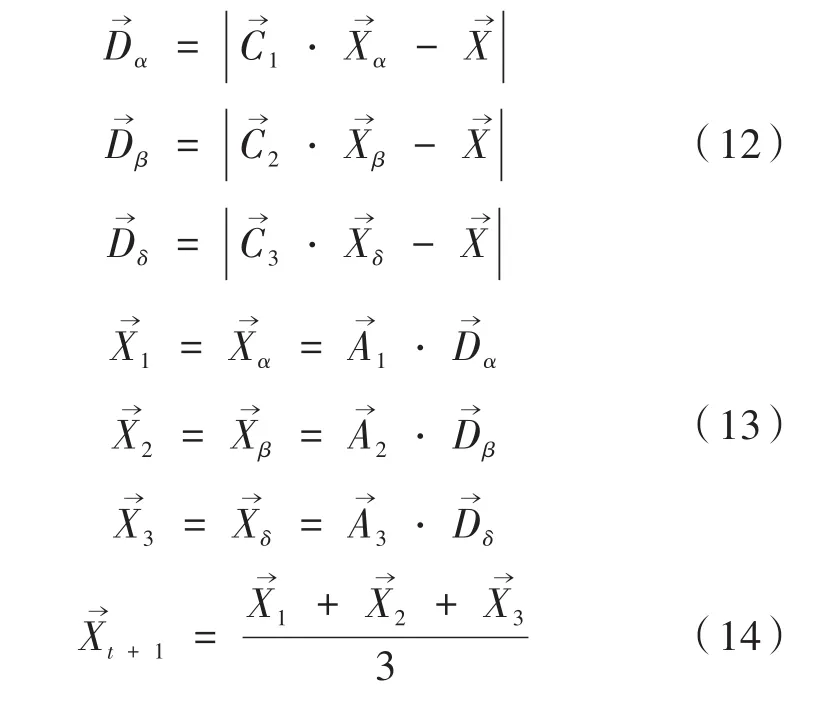
2.2 灰狼优化算法的改进(FGWO)
(1)基于Fuch映射的种群初始化
灰狼群体中灰狼个体的初始位置对GWO算法的寻优性能起着十分重要的作用,灰狼群体的初始位置越均匀,算法的寻优速度越快,效率也越高。原始的GWO算法使用随机的方式初始化种群,这种方式无法保证灰狼个体的健壮性。混沌序列具有良好的随机性,遍历性以及规律性的特点[13],混沌化灰狼的初始种群,能够使得灰狼个体质量更好。采用文献[14]中的Fuch混沌映射进行初始化,其数学表达式如下[14]:
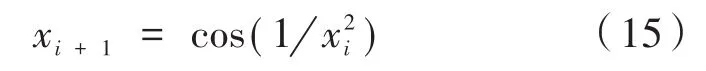
上式求取的混沌序列xi在相对应的空间中可以转换为yi。
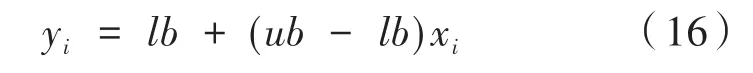
其中,ub、lb分别是yi的上限和下限。
利用Fuch混沌序列产生相对应的反向解:
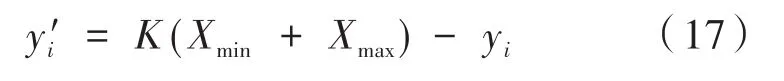
其中,K∈ [0,1],表示yi的反向解;Xmin表示yi的最小值,Xmax表示最大值。
(2)基于Cat混沌映射的扰动算子
为进一步提高GWO算法的寻优性能,选择混沌序列对灰狼群体进行混沌扰动。考虑到Logist映射和Tent映射对参数设置和数据要求较高等问题,本论文将结构较为简单且具有更好的遍历性和更快的迭代速度的Cat映射来进行混沌扰动,其数学表达式为:
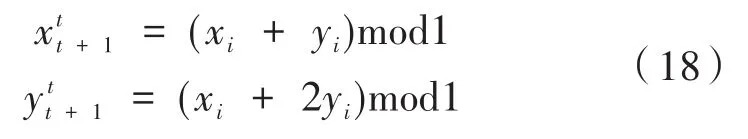
式中,xmod1=x-|x|;t表示混沌迭代次数。扰动算子如下:
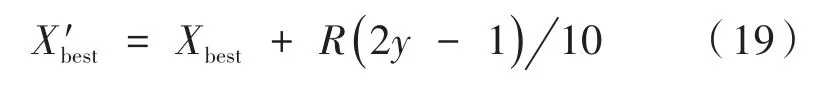
(3)引入个体记忆功能
Cat混沌映射的扰动算子仅仅考虑了灰狼群体的最优解但是却忽略了灰狼每个个体自身的经验,因此将粒子群算法的记忆功能与GWO算法结合,以此来增强算法的寻优速度。新的位置更新方程如下:
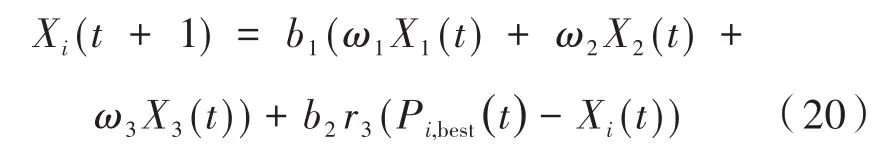
式中,r3∈ [0,1];b1、b2分别表示群体交流系数与个体的记忆系数,选择b1=b2=0.5;Pi,best为第i只灰狼个体以往遍历的最优位置信息;ω1、ω2、ω3为惯性权重系数,通过调节α、β、δ狼的权重比例,能够动态权衡算法的全局及局部搜索能力,公式如下:
采用邻苯二甲醛(OPA) 分光光度法测定游离氨基氮方法计算玉米醇溶蛋白的酶解度[10]。酶解度按公式(1) 进行计算。

FGWO算法步骤可总结如下:
步骤1:初始化灰狼种群的个体位置信息,种群大小,迭代次数,群体交流系数和个体记忆系数。
步骤2:按照式(15)—式(17),对灰狼的初始种群进行Fuch混沌初始化。
步骤3:计算每个灰狼的适应度值,将排名前三的适应度值记为 Fitnessα,Fitnessβ,Fitnessδ,同时保留对应灰狼个体的位置。
步骤4:更新α,以及系数向量A和C。
步骤5:按照式(18)、式(19),对灰狼群体进行混沌扰动,得到此时的灰狼群体的位置和新的前三个适应度值。
步骤7:将上述新的和原先的Fitness值进行对比,更新得到最优的Xα,Xβ,Xδ的位置。如果迭代结束则输出最优解Xα,否则返回步骤3。
2.3 评价函数
在掩模优化问题中,如何评估掩模成像质量的优劣非常关键。掩模成像质量即掩模曝光后的光刻胶图形与目标图形的误差,误差越小表示光刻胶图形与目标图形越接近,掩模成像质量越好[15]。
评价函数在整个优化方法中有着重要的作用,设计一个适当的目标函数并结合合适的优化算法,能使优化速度更快,不易陷入局部最优,最终得到的效果也会更好。将图形误差(PE)定义为优化后的数字掩模成像图形与原始掩模图形对应的像素灰度值相减的平方和。则评价函数可设置为:
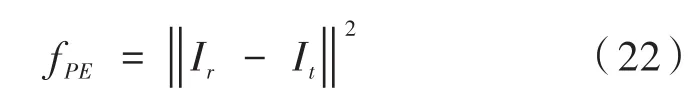
其中,Ir为目标图形;It为掩模经过光刻系统之后成像图形;fPE为适应度值。PE值越大,则表示优化效果越差。
3 仿真分析
3.1 算法收敛性仿真对比与分析
为了验证改进的灰狼优化算法(FGWO)性能,除了传统的GWO算法和PSO算法外,还将它与 SFL-GWO[16]和 LGWO[17]在 四 个 维 数 皆 为 30的测试函数下进行寻优测试,每个测试函数理论最优适应度都为0。测试函数如下:
(1)Sphere函数:-100 <xi< 100,i=1,2,3,…,n
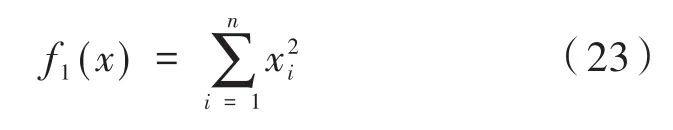
(2)Ackley函数:-32 <xi< 32,i=1,2,3,…,n
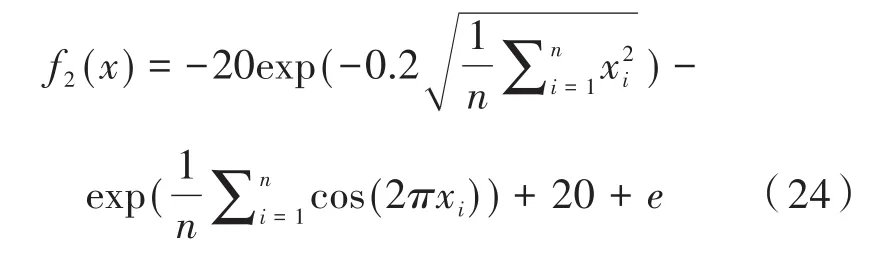
(3)Rastrigrin函数:-5.12 <xi< 5.12,i=1,2,3,…,n
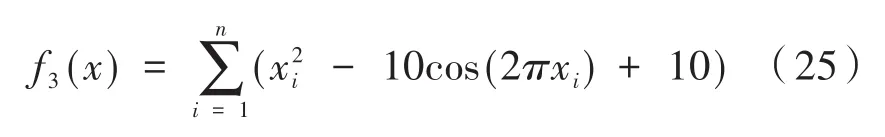
(4)Griewank函数:-600<xi<600,i=1,2,3,…,n
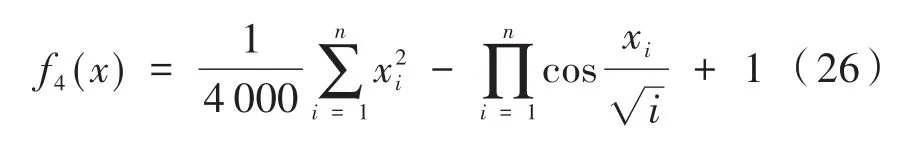
列出了4种测试函数的定义形式、名称、寻优范围。对它们的优化结果是评价算法优劣的重要指标。
从图2可知,FGWO算法的收敛曲线在迭代一开始迅速下降,表明基于Fuch映射的种群初始化方法有效提高了算法的收敛速度,而且在整个迭代寻优过程中,FGWO算法相较于其他算法没有陷入过停滞;另外,FGWO算法的收敛精度与其他算法相比具有明显优势,这与迭代后期扰动算子和个体记忆功能有效提高了算法的局部开发能力相关。
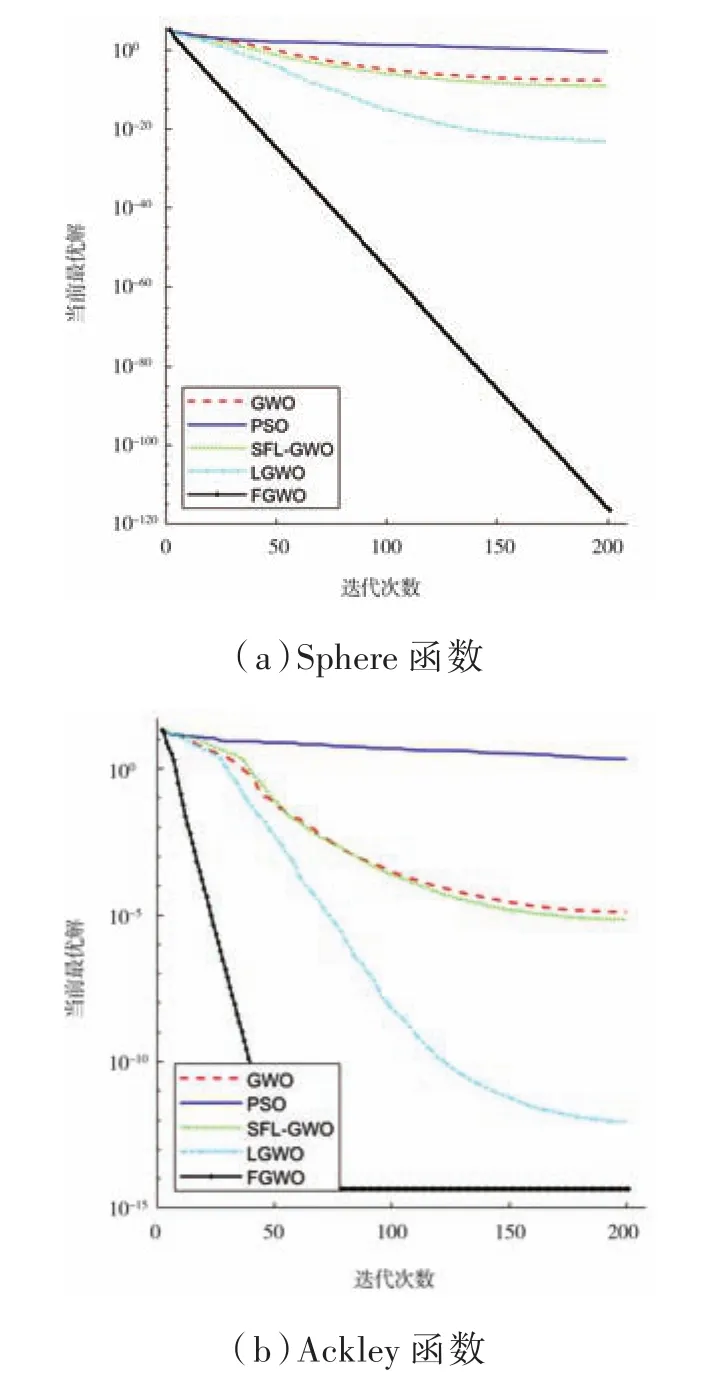
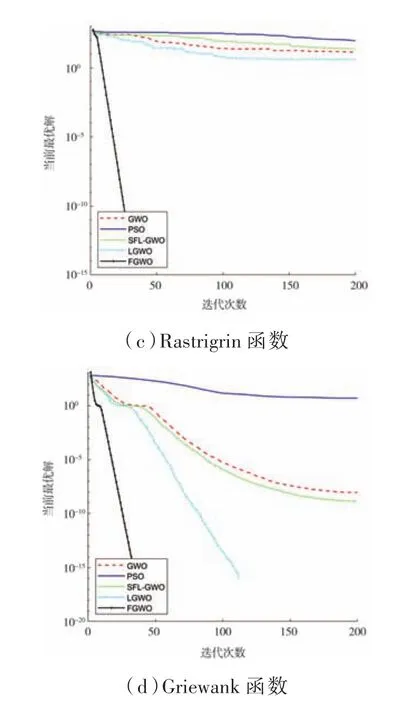
图2 四种函数收敛曲线
表1为所有算法对每个测试函数进行的20次重复的实验结果对比。使用20次测试结果的最优值、标准差、平均值作为算法性能的评价指标。最优值体现了算法的寻优能力,标准差可以体现算法是否稳定,平均值则体现了算法的精度。从表1的对比结果可以看出FGWO算法的最优值优于GWO算法、PSO算法、SFL-GWO算法以及SFL-GWO算法,这表明了FGWO算法在寻优能力上较强。通过对比所有算法的平均值和方差也可以体现FGWO算法更稳定,寻优精度也更高。
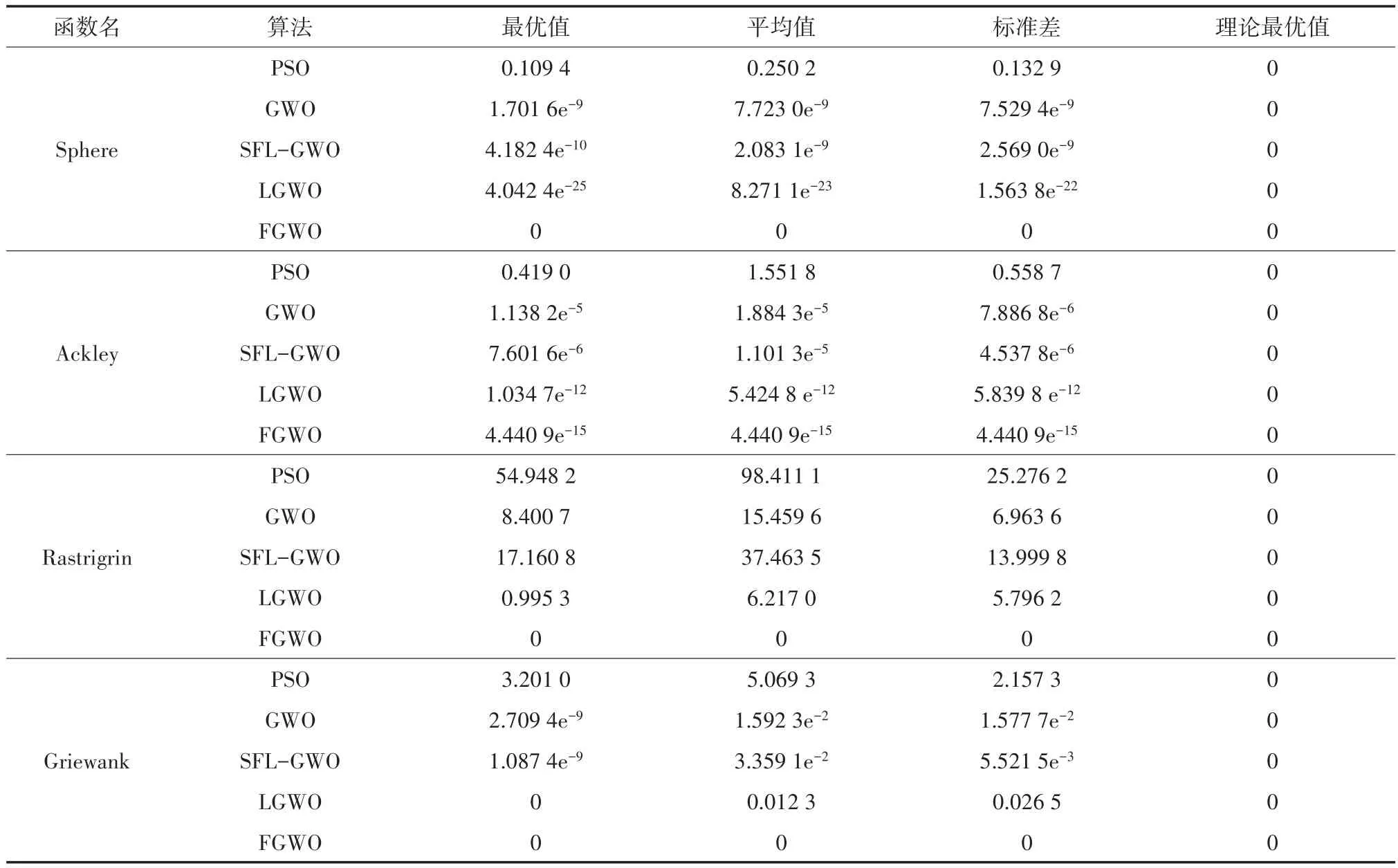
表1 基准测试函数结果对比
3.2 图像质量改进仿真与分析
为了验证该方法的有效性,将改进的灰狼算法与SFL-GWO算法和LGWO算法在掩模优化上进行仿真对比。光刻成像模型公式中单个像素的峰值光强H0=28.312×10-3,沿着xi或者yj方向的1/e2高斯半径ω0=90.074,像素大小p=15.3µm。灰狼种群数量均为50,最大迭代次数是200。每个像素的取值为0或1,初始适应度值为100,评价函数阈值fPE=0,首先,将掩模尺寸设置为80×80像素点。
最终结果如图3所示,可以看到经过SFL-GWO算法和LGWO算法优化后,PE值从96分别下降到了57和44,经过FGWO算法优化后,PE值下降到了10,与前面两种算法相比,PE值分别下降了82.46%和76.74%。

图3 不同算法优化后的简单掩模图形与空间像
为了进一步验证FGWO算法的性能,设计了较为复杂的图形再次进行仿真实验,其尺寸为184×184像素大小,其他条件不变。
最终结果如图4所示,通过结果可以看出,与SFL-GWO算法和LFWO算法相比,FGWO算法优化后PE值从2 962和2 199下降到549,分别下降了81.46%和75.03%。

图4 不同算法优化后的复杂掩模图形与空间像
4 实验验证
为了进一步验证FGWO算法优化后的掩模图形改善光刻成像质量的有效性,搭建如图5所示的实验平台,本次实验使用分辨率为1 024×768的DMD、波长为405 nm的激光光源、型号为BL-SC1600的显微镜。通过上位机将图3(a)、图3(c)、图3(e)、图3(g)与图4(a)、图4(c)、图4(e)、图4(g)两类不同尺寸优化后的掩模图形数据处理后生成二进制位图数据。并将这些二进制数据通过USB接口传输到DMD的缓存芯片中,最后经过涂胶、前烘、曝光、显影等一系列操作之后,可以得到不同算法优化后掩模的光刻图形,如图6和图7所示。

图5 光刻平台

图6 简单掩模图形不同算法优化后实验对比

图7 复杂掩模图形不同算法优化后实验对比
在实验过程中由于实验条件的限制,比如无法提供绝对无光曝光显影环境、光刻平台存在调配误差、光刻胶涂抹不够均匀等,这些因素导致最终产生的光刻图形与仿真的空间像存在些许误差,但是也基本吻合。从图6与图7中可以清晰地观察到FGWO算法优化后的两类掩模光刻图形明显优于其他两类算法优化的光刻图形。
5 结论
提出了一种基于改进灰狼优化算法的数字光刻质量优化方法。使用两种不同的掩模进行验证,结果表明,与SFL-GWO算法和LGWO算法相比,FGWO算法优化掩模后图像误差分别降低了82.46%、76.74%和81.46%、75.03%。同时,通过实验结果可以看出,同一实验环境下,FGWO算法优化后掩模光刻图形质量较之SFL-GWO算法和LGWO算法得到了很大的改善。在未来的工作中,可以将其他因素,比如光源和物镜等加入到光刻优化中,进一步提高数字光刻图形质量。

