基于小波相干的波流相关性分析

张 瑞, 类淑河

(1. 太原工业学院,山西 太原 030008; 2. 中国海洋大学 数学科学学院,山东 青岛 266100)

引 言

波浪和海流几乎总是同时存在，各自独立又相互影响，构成了海洋动力机制必不可少的组成部分。波浪和海流间的相互作用对许多海洋现象也有着重要影响，比如，风暴潮、海洋表层温度、海底泥沙运动等等。理解其物理机制和过程，对开发利用海洋资源、预防海洋灾害等方面有实际应用价值。在实际情况中，波流场中的流速沿水深是非均匀的，即流速随着水深发生变化[1]。关于波浪与非均匀流相互作用的研究，学者从理论分析、数值模拟、现场观测和实验研究等方面进行了探讨[2-5]。

实验所得的波流信号通常离散且不连续，本质上为时间序列。可以从两个方面讨论时间序列的相关性，即时域分析和频域分析。时域分析是在时间尺度上研究序列的变化，常用的方法有线性相关系数、Granger因果分析、Copula函数等[6]，随着机器学习优越性的体现，卷积神经网络也成为有力的工具[7]。频域分析是把时间序列视为不同频率分量的叠加，交叉谱是常用于分析相关性的方法[8-9]。但是，仅从单一角度分析得到的结论未必对所有时间范围和频率均显著相关，小波相干可同时从时域和频域两角度分析时间序列间的动态相关性[10]。波流信号作为时间序列，同样可采用小波相干进行相关性分析，使得分析波流在不同时间尺度下的周期相关性成为可能，并有望产生实际应用价值。

本文主要目标是基于交叉谱和小波相干对波流相关性进行分析。第一部分介绍交叉谱和小波相干的定义及估计方法。第二部分基于实验数据，采用交叉谱和小波相干估计不同水深时的波流相关性。第三部分给出了相应的结语与讨论。

1 理论基础

1.1 交叉谱及估计

设二维零均值平稳时间序列{x(t),y(t)}，t=0,±1,±2,…，则x(t)与y(t)的互相关函数定义为：

Rxy(τ)=E[xtyt+τ],τ=0,±1,±2,…

(1)

其中E[.]表示数学期望。

(2)

为排除量纲影响，对交叉谱标准化后平方，引入凝聚谱：记x(t)的单谱为Sxx(f)，y(t)的单谱为Syy(f)，则两时间序列的凝聚谱可表示为:

(3)

凝聚谱是从频域角度对相关性进行分析的方法，其取值范围为[0,1]。凝聚谱值越接近于1，说明x(t),y(t)在相应频率分量上的相关性越强，相反，若取值越接近于0，相关性越弱。凝聚谱可采用Welch方法[11-12]、多窗谱方法(Multitaper Method，简称“MTM方法”)[13]和最小方差无失真响应方法(The Minimum Variance Distortionless Response Method，简称“MVDR方法”)[14]等进行估计。对实验室波流信号来说，文献[9]从数值模拟和实验室数据两个角度分析比较，发现MVDR方法有更强的相关信号识别能力和频率分辨能力，不易出现伪峰，估计结果更加可靠。通常，凝聚谱估计值均大于0，但并不意味着两信号在任何频率上均相关，需进行非零相关性检验[11,15]。

1.2 小波相干

小波指小区域的波，定义为：

(4)

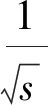
时间序列x(t)的连续小波变换定义为：

(5)

其中，*代表复共轭，x(t)∈L2。

设对于时间序列x(t),y(t)，连续小波变换分别为Wx,Wy，则小波交叉谱定义为:

(6)

小波相干可由小波交叉谱标准化后平方得到，定义为:

(7)

其中，S为平滑算子。小波相干在[0,1]区间取值，其值越接近于1，x(t),y(t)在对应频率和时间段上相关性越强；相反，其值越接近于0，则相关性就越弱。由于小波相干理论分布未知，其统计显著性基于蒙特卡洛方法检验[10]。

2 实验室波流数据分析

2.1 数据及其预处理

实验在中国海洋大学物理海洋实验室大型风-浪-流水槽中进行，水槽长65 m，宽1.2 m，高1.5 m，实验时水深d约为0.7 m，主导波长L约为0.7 m，相对水深>0.5，可视为深水[1,16]。波面位移采用实验室自主研发的OUC-2型钽丝测波仪(以下简称“测波仪”)测量，采样频率大约为26.78 Hz，数据记录满15 000个点后自动停止，时长约9 min 20 s。水下的流速采用声学多普勒流速测量仪(ADV-1流速测量仪，以下简称“ADV”)测量，ADV的采样频率为25 Hz，相应数据长度在14 000个点左右。

不失一般性，选取34.2 m风区、风速8 m/s时，ADV探头深度15,20,25,30,35,40 cm六个水平下的波面位移和铅直流速信号。由于ADV与测波仪的采样频率不同，为进行下一步分析，对铅直流速序列进行线性插值，使其与波面位移序列对应。铅直流速有两次观测，将两次观测取平均以减小测量误差，又流速信号不平稳，用Butterworth滤波器滤去频率小于0.5 Hz的信号，去除低频信号，使时间序列平稳。最后将波面位移和预处理之后的铅直流速序列进行标准化。

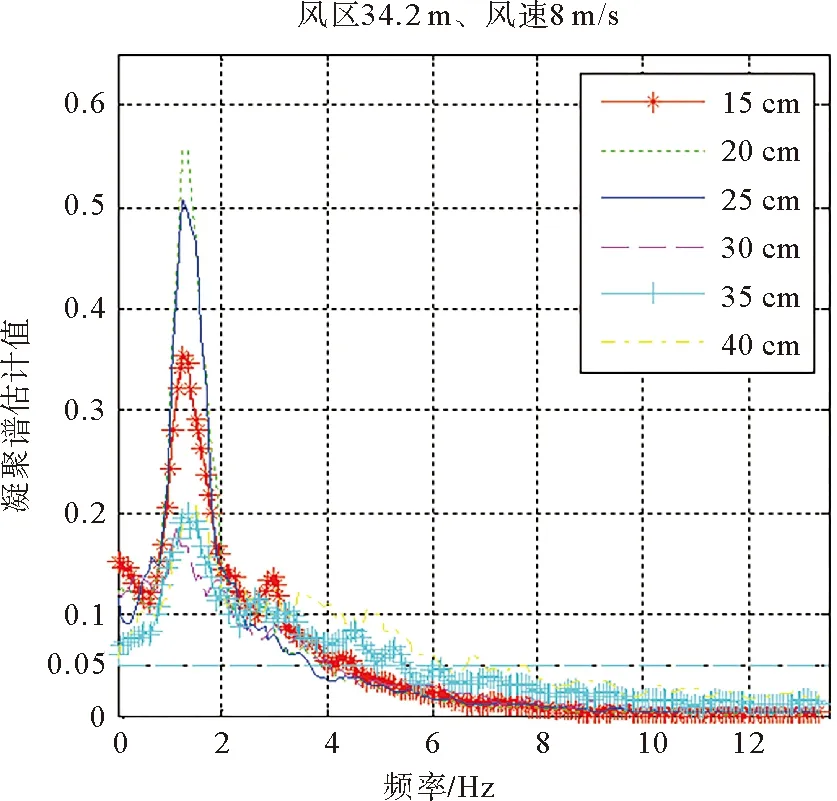
图1 凝聚谱估计Fig.1 The estimation of magnitude-squared coherence

2.2 交叉谱估计

采用MVDR方法(窗宽256，分辨率为400)对六组波流信号进行凝聚谱估计，结果如图1所示，横轴为频率，其单位为Hz，纵轴为凝聚谱估计值，无量纲。做非零相关性检验，在0.95的置信水平下，临界值为0.054。即凝聚谱估计超过0.054，认为波流在相应频率上显著相关。

ADV探头处于不同深度时，凝聚谱估计走势相似，在频段0～4 Hz，凝聚谱估计均高于临界值，呈现出明显的谱峰，表明在该频段内波流信号显著相关。随着频率增加，凝聚谱估计呈现衰减趋势，约大于5 Hz之后，凝聚谱估计小于临界值，表明在该频段相关性变得不显著。但是在谱峰频率fp附近，不同水深的凝聚谱估计值存在明显差异。当测量深度为20 cm时，谱峰值最高，大约为0.55。当测量深度为15 cm时，谱峰值约为0.35。当测量深度为25 cm时，谱峰值为0.50。当测量深度大于30 cm时，谱峰值明显偏小，约在0.20。综上发现，在中层水深时，波流相关性最强，随着深度的增加或减小，相关性程度大致呈下降的趋势。

2.3 小波相干估计

对六组实验室波流信号进行小波相干估计，结果如图2所示，横轴为时间，纵轴为周期，单位均为采样间隔，约为0.037 s。所围区域颜色越暖，对应小波相干估计值越接近于1，波流信号的相关性越强；反之，若所围区域颜色越冷，估计值越接近于0，波流信号的相关性越弱。ADV探头处于不同深度时，小波相干估计图非常相似，纵轴刻度约为10～40时，即周期为0.37～1.48 s，对应频率约为0.67～2.70 Hz，图像出现带状暖色区域，说明在该频率区间上波流相关性较强，此结论与凝聚谱估计结果(0～4 Hz)相比，有重叠但范围相对小。

在带状暖色区域，不同深度的小波相干估计图又存在差异。当位于水深15 cm处时，横轴3 000～7 000之间，即采样中前期，暖色区间相对密集，波流相关性强，相比较而言，在其他时间段内相关性较弱；当位于水深20 cm处时，在横轴500～14 000之间，即采样中后期，暖色区域密集，持续时间长，说明在该时间段波流相关性较强；当位于水深25 cm时，在横轴5 000～11 000之间暖色区域密集，说明在采样中期波流相关性较强。当位于水深30 cm及以上时，暖色区域明显稀疏，说明只在某些短时间段存在较强相关性。对比发现，位于中层水深时，波流呈现强相关性的时间段最长，在浅层和深层水深时，波流呈现强相关性的时间段较短。

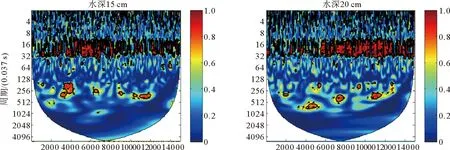
图2 小波相干估计Fig.2 The estimation of wavelet coherency

3 结语与讨论

对实验室波流信号进行凝聚谱估计，结果发现，不同水深时，在频段0～4 Hz波流信号均显著相关，随着频率增加，约大于5 Hz之后，相关性变得不显著。但是在谱峰频率fp附近，不同水深时的凝聚谱估计值存在明显差异，在中层水深时，估计值最大，波流相关性最强，随着深度的增加或减小，相关性程度大致呈下降趋势。

对实验室波流信号进行小波相干估计，结果发现，不同水深处，频率约为0.67～2.70 Hz时，小波估计图均出现带状暖色区域，说明在该频段波流相关性较强，此结论与凝聚谱估计结果(0～4 Hz)相比，有重叠但范围相对小。在带状暖色区域，不同深度的小波相干估计图又存在明显差异，位于中层水深时，暖色部分明显集中，波流呈现强相关性的时间段最长，在浅层和深层水深时，暖色部分相对稀疏，波流呈现强相关性的时间段较短。

依上述两种方法分析的结果可知，波流信号在频率0～4 Hz或稍小范围存在相关性，但是不同水深时，相关性程度有所差别。在中层水深，波流相关性较强，且持续时间最长；在浅层和深层水深时，波流相关性有下降的趋势，且持续时间相对较短。