Global Existence and Time-decay Rates of Solutions to 2D Magneto-micropolar Fluid Equations with Partial Viscosity

LU Cheng and WANG Yuzhu

School of Mathematics and Statistics, North China University of Water Resources and Electric Power,Zhengzhou 450011,China.

Abstract. In this paper,we investigate the initial value problem for the two-dimensional magneto-micropolar fluid equations with partial viscosity. We prove that global existence of smooth large solutions by the energy method. Furthermore, with aid of the Fourier splitting methods, optimal time-decay rates of global smooth large solutions are also established.

Key Words: Magneto-micropolar fluid equations with partial viscosity;global smooth large solutions;time-decay rates.

1 Introduction

In this paper,we investigate global existence and time-decay rates of smooth large solutions to two-dimensional magneto-micropolar fluid equations with partial viscosity

with the initial value:

The magneto-micropolar fluid equations describes the movement of conductive micropole fluid in the magnetic field,and has been widely used in the fields of shipbuilding industry,aerospace,geophysics,hydrodynamics and meteorology,etc.The complexity of the mathematical structure of the equation has attracted extensive attention in the field of physics and mathematics. The global regularity and finite-time singularities of the large initial value solution of the three-dimensional magneto-micropolar fluid equations are still a difficult and important problem. We refer to[1-13] and[14] for existence and uniqueness of strong solutions,regularity criteria of weak solutions and blow-up criteria of smooth solutions to magneto-micropolar fluid equations.

When partial viscosities disappear,mathematical analysis of(1.1)becomes more complicated.We recall the global existence and and decay estimate of solutions to the incompressible magneto-micropolar fluid equations with partial viscosity for our purpose. A few results have been established, we may refer to [15-23]. Cheng and Liu [16] studied the two-dimensional anisotropic magneto-micropolar fluid equations with vertical kinematic viscosity, horizontal magnetic diffusion and horizontal vortex viscosity and global regularity was established. Global regularity of the classical solutions for the twodimensional magneto-micropolar equations with partial dissipation was proved by Regmi and Wu[18]. Ma[17]extended the results in[18]to other mixed partial viscosities cases and global existence and regularity were established. Shang and Gu [20] established global classical solutions to 2D magneto-micropolar equations with only velocity dissipation and partial magnetic diffusion by using the special structure of the system and the maximal regularity property of the 1D heat operator. For 3D magneto-micropolar fluid equations with mixed partial viscosity, mathematical analysis of global existence becomes more complicated. Wang and Wang[21]studied the global existence of smooth solutions for 3D magneto-micropolar fluid equations with mixed partial viscosity by energy method.Very recently,the second author of this paper and Li[22]established global well-posedness of classical small solutions and generalized the results in[23].

Ifv=0 andη=0,then the equations(1.1)is reduced to the incompressible MHD system,which describes the dynamics of electrically conducting fluids arising from plasmas,liquid metals,salt water or some other physical phenomena. It is well known that MHD system is the incompressible Navier-Stokes equations coupled with the magnetic fields.Hence,it is not surprising that the question of finite time singularity or global regularity is an outstanding open problem in the mathematical fluid mechanics. Due to the importance and challenge of the problem on global regularity and finite-time singularities of MHD equations with partial viscosity, the global well-posedness of MHD equations with partial viscosity has attracted the attention of many mathematicians, and lots of interesting results were established(see,e.g.,[24-40,43-45]).

Inspired by the recent works[17,20,22,23],for the incompressible magneto-micropolar equations with mixed partial viscosity and[25,28,41]for the incompressible MHD equations with mixed partial viscosity,the main aim of this paper is to investigate the global existence and time-decay rate of large smooth solutions to the problem(1.1),(1.2).

Next,we start our main results as follows:

Theorem 1.1.Let m≥3be integer. Assume that u0,v0,B0∈Hm(R2)and∇·u0=∇·B0=0,then the problem(1.1),(1.2)has a unique global smooth solution

Remark 1.1. Because there is no any small assumption on the initial value, the solution obtained in Theorem 1.1 is a large one.

The second main purpose of this paper established global existence and decay rate of smooth solutions obtained in Theorem 1.1 to the problem(1.1),(1.2).

Theorem 1.2.Assume that the conditions of Theorem1.1hold. Let µ1=µ2and1 ≤p＜2,suppose that u0,v0,B0∈Lp(R2), then the global smooth solution(u,v,B)to the problem(1.1),(1.2)satisfies

for0≤k≤m,where the constant C depends on the norms of the initial data.

Remark 1.2. The time-decay rate (1.4) of solutions itself and its all order derivatives is optimal under the assumptions of Theorem 1.2 since the decay rate (1.4) is the same as that of heat kernel.

Remark 1.3. Whenv=η=0 andp=1,the time-decay rate(1.5)has been recently obtained by Zhang,Dong and Y.Jia[41]. Therefore,the result in Theorem 1.2 generalize that of 2D MHD equations with partial dissipation established in[41].

The paper is organized as follows. In Section 2, we state some important inequalities. In Section 3,we prove that the global existence of smooth solutions to the problem(1.1),(1.2) without any small assumptions on the initial value. In Section 4, we establish the optimal time-decay rates of global smooth large solutions established in Theorem 1.1 by developing the generalized Schonbek's Fourier splitting methods.

2 Preliminaries

In order to prove global existence and time-decay rate of large smooth solutions to the problem (1.1), (1.2), we state the following lemmas which play central roles in proving our main results.

The following lemma is used to deal with partial dissipation.

Lemma 2.1.Suppose u=(u1,u2)is divergence free and for any nonnegative integer m,then

Proof.Integration by parts and ∇·u=0 ensure that(2.1)holds. We may refer to[41]for anther proof.

To deal with the nonlinear terms,Lemmas 2.2 and 2.3 are introduced.

3 Global existence

In this section,we devote to prove the global existence of smooth solution to the problem(1.1),(1.2). More precisely,we will prove the Theorem 1.1. Without loss of generality,we assume thatµ1≥µ2,ν1≤ν2.

3.1 Basic L2 estimates

Multiplying(1.1)by(u1,u2,v,B1,B2),respectively,and integrating in R2,we obtain

Lemma 2.1 entails that

Applying ∇·u=∇·B=0,we have

By Cauchy's inequality,we have

Inserting the above estimates into(3.6)yields

3.2 H1 estimates

We directly multiply the equations of (1.1) by (-Δu1,-Δu2,-Δv,-ΔB1,-ΔB2), respectively,and integrate by parts. This leads to

Then adding(3.13)-(3.17)and applying(3.18),we have

本研究发现，血清IgE、IL-4水平与痰EOS呈正相关(P<0.05)；RPB水平与痰EOS呈负相关(P<0.05)，说明血清炎症因子水平越高，患儿肺功能下降越严重，气道炎症反应越重。肺炎支原体感染能够直接或间接促进血清炎症因子大量分泌，进一步说明MP感染能够加重支气管哮喘症状，不利于患儿恢复[20]。

Assumingµ1＞µ2,ν1＜ν2,forJ1+J2,J3+J4,employing Lemma 2.1 and integration by parts,we have

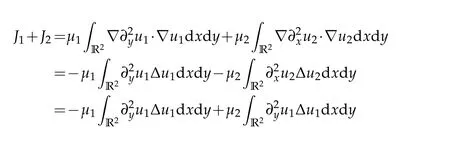
3.3 Hm estimates

We apply ∇mto both sides of(1.1)and then multiply the resulting equations by(∇mu1,∇mu2,∇2mv,∇mB1,∇mB2)and integrate over R2,respectively.It yields

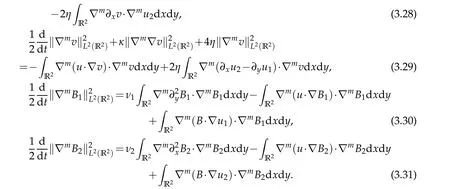
Employing integration by parts,H¨older inequality and Cauchy's inequality,we have the follow facts

We first estimateM1+M2andM3+M4. By using ∇·u=∇·B=0, Lemma 2.1 and integration by parts,we have

ForM5+M6,M7+M8,M9+M10+M11+M12andM13,employing H¨older inequality,Cauchy's inequality,Young inequality,and Lemma 2.2,Lemma 2.3,we have

In what follows,we shall complete the proof of global existence of smooth large solutions.More precisely,we shall prove the Theorem 1.1.

4 Time-decay rates

Our main purpose of this section is to establishL2time-decay rates of solutions itself and all order derivatives of solutions to the problem(1.1),(1.2). More precisely,we prove the Theorem 1.2.

4.1 L2decay of solutions

In this subsection,our target is to obtainL2decay rate of global solutions to the problem(1.1),(1.2).

Lemma 4.1.Let(u,v,B)be a solution to equations(1.1)with initial data(u0,v0,B0)satisfying the initial data as in Theorem1.2. Then we have

Proof.We first consider the initial value problem for the corresponding linear system of(1.1)

with initial data(1.2).

Then,combining(4.5)and(4.6)gives

Lemma 4.3.Let(u,v,B)be a smooth solution to the equations(1.1)with initial data(u0,v0,B0)satisfying the initial data as in Theorem1.2. Then we have

Then we complete the proof ofL2decay rate of global solutions to the problem (1.1),(1.2).

4.2 L2 decay of derivatives

In this subsection,our main purpose is to proveL2decay rate of all order derivatives of solutions.

Proof.For 1≤k≤m,inserting(3.34)and(3.36)into(3.33)yields

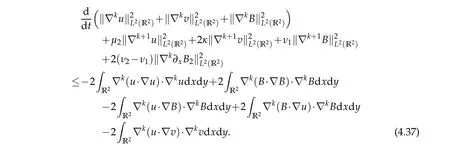
SetU=(u,v,B)T, then we have from (4.37), ∇·u=∇·B=0, (2.2), (2.3) and Cauchy's inequality

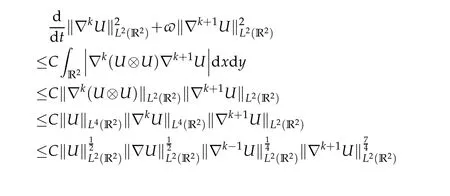
for 0≤s＜t＜∞,which implies that

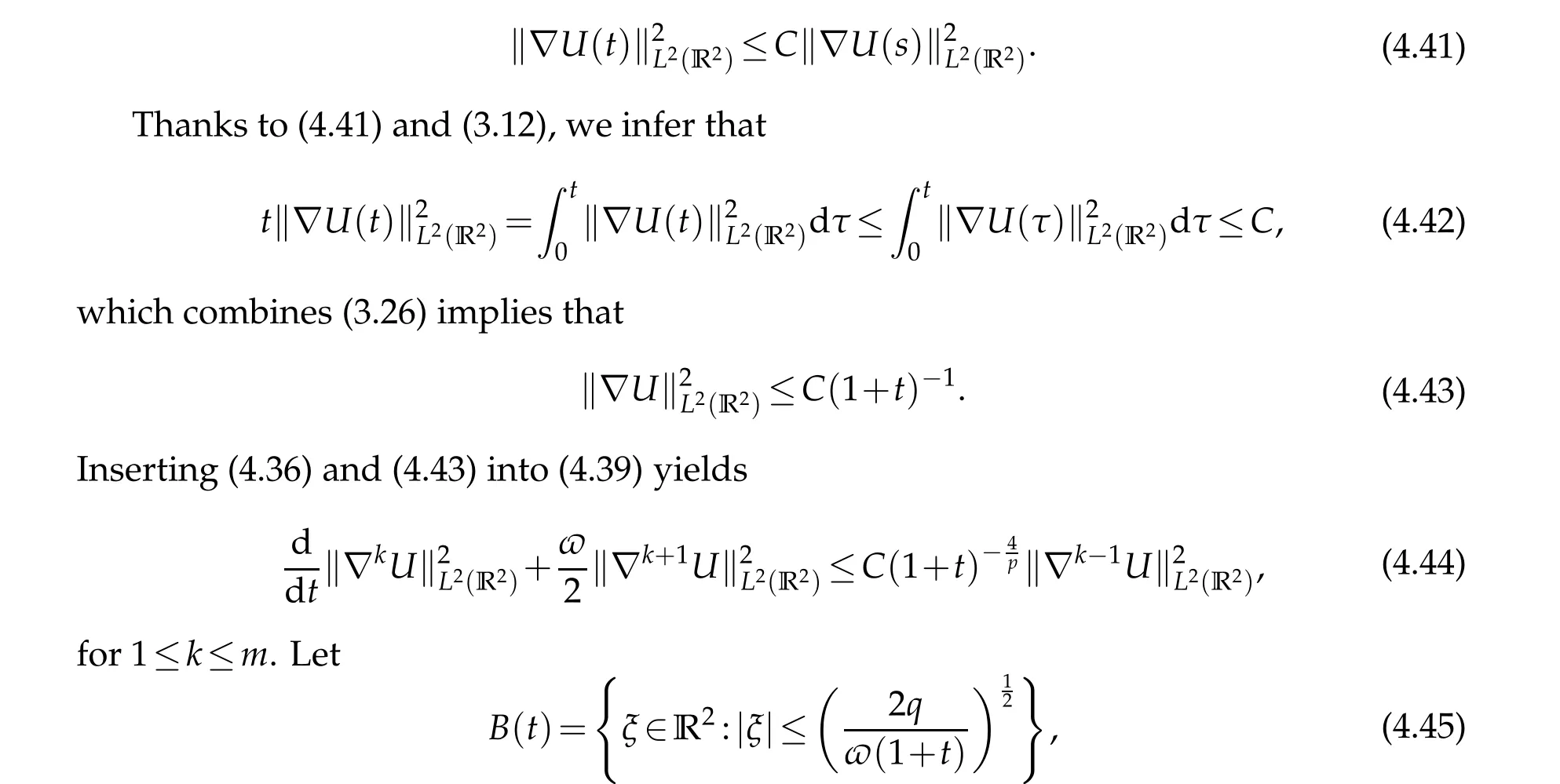
whereq∈N is a large integer, and applying Plancherel's theorem to (4.44) and noting 1≤p＜2,we have

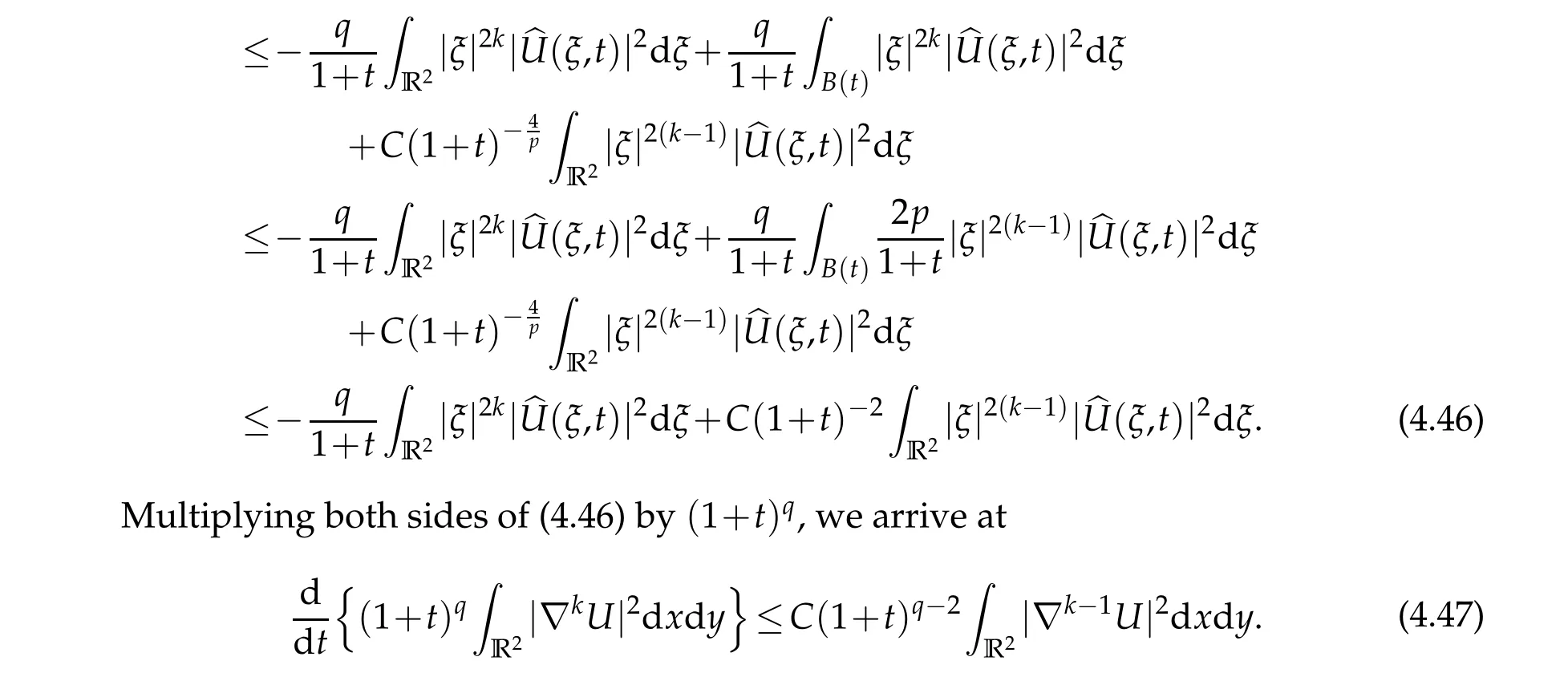
Integrating(4.47)with respect to time yields

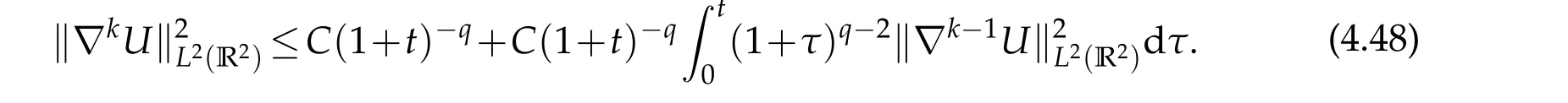
In what follows, we shall prove time-decay rate of all order derivatives in (1.4) by mathematical induction method. Whenm=1,by direct calculation, we have from(4.48)and(4.36)

Then we complete the proof of time-decay rates of all order derivatives of solutions in Theorem 1.2.

Acknowledgement

This work was supported in part by the NNSF of China (Grant No. 11871212) and the Basic Research Project of Key Scientific Research Project Plan of Universities in Henan Province(Grant No. 20ZX002).