Blowup Behavior of Solutions to an ω-diffusion Equation on the Graph

ZHU Lipingand HUANG Lin

Faculty of Science, Xi'an University of Architecture and Technology,Xi'an 710055,China.

Abstract. In this article, we discuss the blowup phenomenon of solutions to the ωdiffusion equation with Dirichlet boundary conditions on the graph. Through Banach fixed point theorem,comparison principle,construction of auxiliary function and other methods, we prove the local existence of solutions, and under appropriate conditions the blowup time and blowup rate estimation are given. Finally,numerical experiments are given to illustrate the blowup behavior of the solution.

Key Words: Simple graph;discrete;blowup time;blowup rate.

1 Introduction

In this paper,we mainly study the blowup phenomenon of the following problem

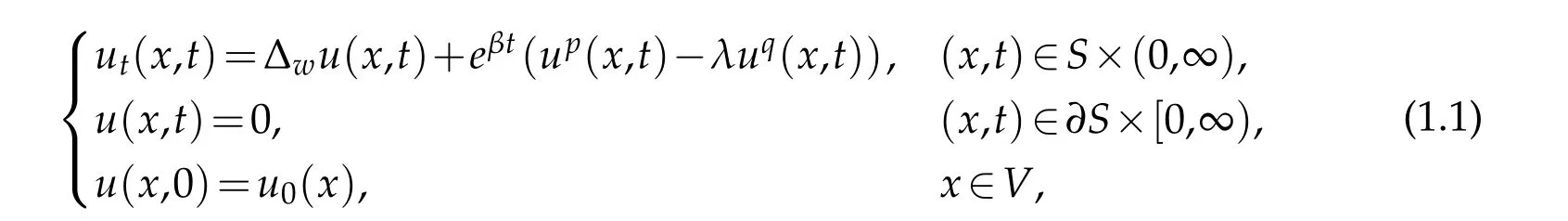
wherep,q,β,λare all greater than 0, and the initial valueu0(x)/≡0 is non-negative.The graphG(V,E,w)is a simple weighted graph with limited connectivity. The setVof vertices on the graph consists of two disjoint subsetsSand∂S.Eis the set of edges of graphG,and weighted functionw:V×V→[0,∞)satisfies:

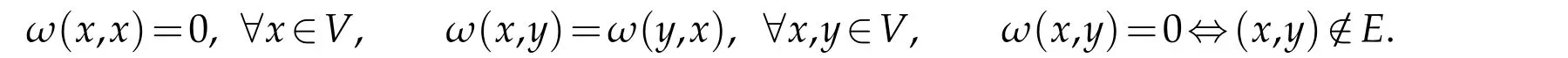
We define the Laplace operator on the graph as that in reference[1]

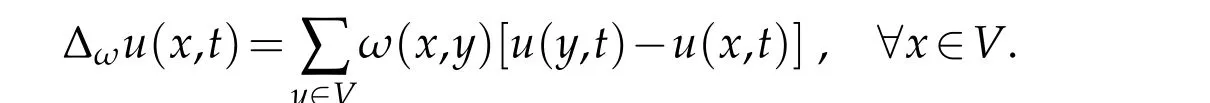
In daily life, after the fireworks ignite the fuse, it rely on the instantaneous burst of gunpowder to generate energy and present colorful scenery. Lithium-ion batteries can cause fires,explosions and other safety accidents under poor temperature and humidity conditions. Ion conductors stimulate polarization phenomenon and other common phenomena can all be attributed to the singular solution models of differential equations.The study of these models will have a great guiding effect on our lives,therefore,the study of the singular phenomenon of the solution has always been a hot issue for mathematicians.As early as 1966,Fujita[2]conducted a pioneering study on the blowup phenomenon of the solution of the semilinear reaction-diffusion equation

on the conditionα＞0 and get some interesting conclusion. When 0＜mα＜2,the Cauchy problem has no non-trivial solution as a whole.When 2＜mαand the initial value is small enough,the solution exists as a whole,and the solution will blow up in a finite time if the initial value is large enough. This great research urges more and more scholars to study the blowup behavior actively,and explore many complex models([3-8])consequently.

In recent years, some scholars have begun to pay attention to the study of singular solutions of evolution equations defined on the network structure. Many objects and their interrelationships are generally represented by a network. In a power system, the network is composed of a number of components and a circuit that transmits electrical signals through certain requirements. In mathematics, the weighted graph is another name for the network. Vertices represent objects and edges represent connections between objects,which is widely used to analyze discrete objects. Scholars have also conducted some in-depth discussions on different boundary value problems.Theω-Laplaceequation on the graph is obtained by modeling the power grid,which has a wide range of applications in various fields.It can be used to simulate the energy flow in the network or the vibration of molecules in[1,9-12],and it can also be used to study dynamic systems and image processing in[13,14]. Chung[1]first defined some concepts of calculus in discrete cases, such as directional derivative, gradient, etc., and he proved that the overall uniqueness of the solution to the inverse problem,and the solubility of boundary value problems of the first and second types under appropriate monotonic conditions.

In[15],Chung also studied a class ofω-heatequations with nonlinear source terms

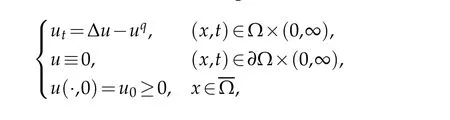
which is a mathematical model of thermal diffusion over a network. The network flow depends on the reaction force proportional to the potential power, and the behavior of the solution depends on the positive and negative ofq-1. If 0 ＜q＜1, the nontrivial solution quenches in finite time. Ifq≥1,the solution is always positive.

Xin [16] considered the quenching and positivity of the solution of theω-diffusion equation with absorption term,and then studied the blowup phenomenon caused by theω-heat equation with reaction term

in [17]. Ifp≤1, each solution is global. Ifp＞1, under appropriate conditions, the non-negative non-trivial solution blows up in finite time, and the upper bounds of the blowup time and the blowup rate under theL∞norm are given. Zhou[18] studied the blowup phenomenon with Dirichlet boundary conditions on the graph. Liu [19] studied the quenching and asymptotic properties of the solution of theω-heat equation with source and internal absorption terms on the graph

Based on the enlightenment of the above work,we discussed the blowup phenomenon of problem (1.1). Firstly, we proved the local existence of the solution by Banach fixed point theorem and give a needed definition. Secondly, the existence of global solution is proved whenp＜q, and then the blowup phenomenon of the solution is discussed under appropriate conditions. Finally,numerical experiments are given to illustrate the accuracy of the theoretical results.

2 The local existence of the solution

In this section,we first define a Banach space and its norm

where

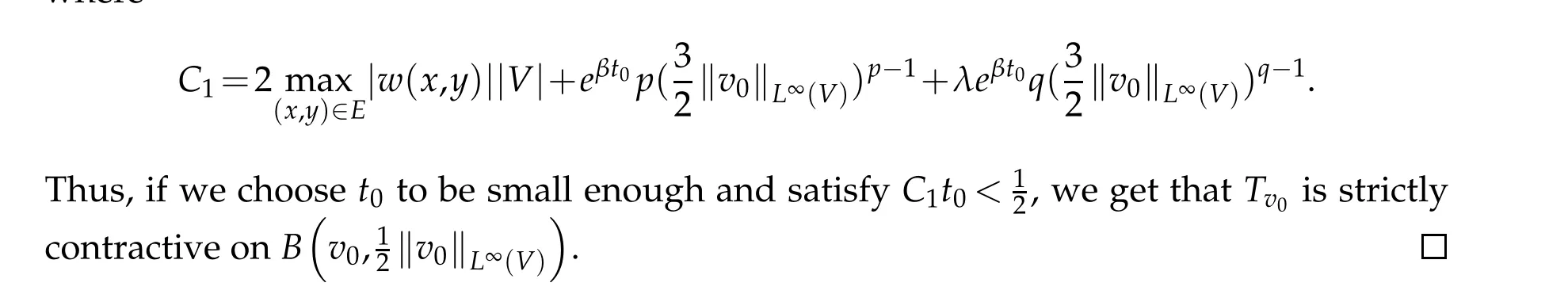
Theorem 2.1.If v0∈C(V)and v0≥0,but v0/≡0,there exists a finite time T such that problem(1.1)has a unique solution in S×[0,T).

Proof.From Lemma 2.1 and Banach fixed point theorem, we obtain the existence and uniqueness of the solution of problem(1.1)in[0,t0). If‖u‖Xt0＜∞,we chooseu(x,t0)as the new initial value and get the solutionu(x,t)defined inS×[0,t1)(t1＞t0). Therefore if‖u‖Xt1＜∞, we can do as before to get the solution defined inS×[0,t2)(t2＞t1) again,which shows that there exists a finite timeT＞0 such that problem(1.1) has a unique solution inS×[0,T).

Definition 2.1.If non-negative function¯u(x,t)∈C(V×[0,T))satisfies

we call¯u(x,t)a supersolution of(1.1). If u(x,t)satisfies the reverse inequality in(2.2), then u(x,t)is defined as a subsolution of problem(1.1).

Theorem 2.2.Let¯u(x,t)and u(x,t)be the supersolution and subsolution of problem(1.1)respectively,and there exists a point y∈S such that ω(x,y)/=0for any(x,t)∈V×[0,T). Then for any(x,t)∈V×[0,T),we have¯u(x,t)≥u(x,t).

Proof.Letv(x,t)=u(x,t)-¯u(x,t),T1＜T,∀(x,t)∈V×[0,T1),we have

By the conclusion in[18,Theorem 3.2],we obtain

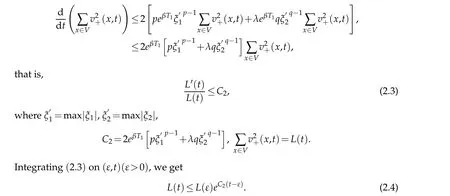
By use of the definition of subsolution,supersolution andv+(x,t),we derivev+(x,0)=0 and thenL(0)=0. From(2.4),we concludeL(t)≤0 whenε→0,which contradicts withL(t)≥0. SoL(t)≡0. Therefore,v(x,t)≤0,which meansu(x,t)≤¯u(x,t).

3 Blowup phenomenon and global solution

Theorem 3.1.If p＜q,then all solutions of problem(1.1)are global.

Proof.To get the conclusion,we only need to find a global supersolution of problem(1.1).

For a given positive numberβ,we chooseC3=λ1

p-qand ¯u=C3eβt,and we have

By the definition of supersolution we know that ¯u=C3eβtis a supersolution of problem(1.1),so all solutions of problem(1.1)are global.

i.e.,the solution of problem(1.1)on graph G blows up in infinite time in the case of p=1,and in the case of p＞1, the solution blows up in a finite time T. Here λ1is the principal eigenvalue of eigenvalue problem

BecauseE(0)is sufficiently large,we obtainE(t)is large astis sufficiently small. So after some simple calculations we can conclude thatE'(t)＞0. Thus

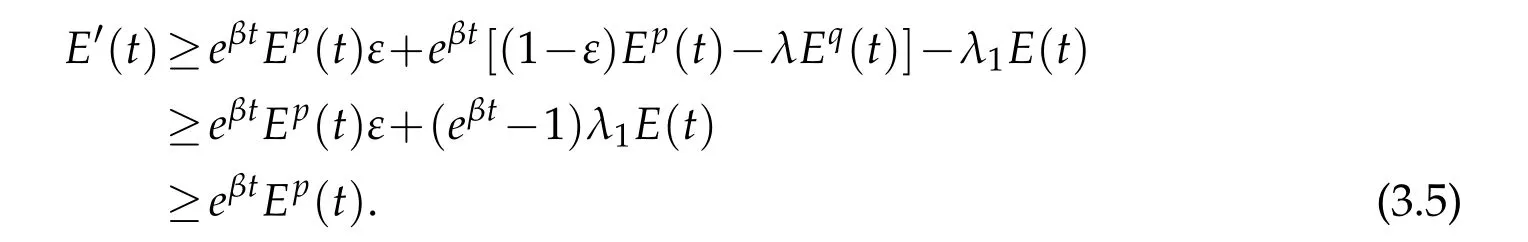
Whenp=1, we integrate (3.5) on (0,t), lett→+∞, and get the conclusionE(t)→+∞,which shows the solution blows up in infinite time. Whenp＞1, from (3.5), we obtain that the solution blows up in a finite timeT.

Theorem 3.3.If p＞1＞q,then the solution u(x,t)of problem(1.1)blows up in a finite time T,and satisfies

Theorem 3.4.Suppose that p=q,u0(x)/≡0is non-negative.

(1)Let p=q=1,when λ＜1,λ*1＜1-λ and u0(x)＞0,the solution of problem(1.1)blows up in infinite time.

(2) Let p=q＞1, when λ≥1and u0(x)is sufficiently small, the solution of problem(1.1)is global.

(3) Let p=q＜1, when λ＜1and u0(x)is sufficiently small, the solution of problem(1.1)is global.

(4)Let p=q＞1,when λ＜1and u0(x)is sufficiently large,the solution of problem(1.1)blows up in finite time.

From the definition ofh(x,t)and(3.8),we haveg'(t)=g(t)(1-λ-λ*1)＞0,andh(x,0)≤‖u0‖L∞(V), thush(x,t) increases monotonically with respect tot. Then combining the condition

we derive thatr(x,t)is a supersolution of problem(1.1)and the solution of problem(1.1)is global consequently.

(4)Suppose thatu(x,t)is the solution of the problemut(x,t)=Δwu(x,t)+up(x,t)with Dirichlet boundary condition and after some calculations we conclude thatu(x,t) is a subsolution of the (1.1) whentis suitable large. From [17] we know that the solutionu(x,t) blows up in finite time whenp＞1 under some conditions. So the solution of problem(1.1)also blows up in finite time.

4 Numerical experiment

In this section,we give an example to illustrate our conclusion. The graphG1(V,E,ω)is shown in Figure 1,V={x1,x2,...,x8},S={x1,x2,x3,x4},∂S={x5,x6,x7,x8},and the weight functionω(x,y)≡1. Then the problem(1.1)can be written as:

letU=(u1,u2,u3,u4)⊺and coefficient matrix

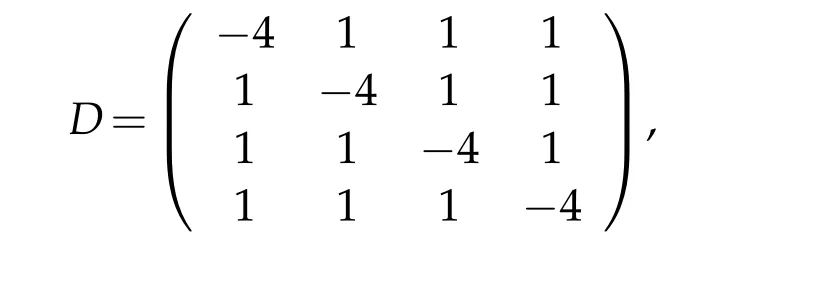
then(4.1)can be rewritten as

By use of the difference method,we have

whereUn=(u(x1,nΔt),u(x2,nΔt),u(x3,nΔt),u(x4,nΔt))Tand Δtis the time interval.Here we chooseσ1=2,σ2=4,σ3=6,σ4=8,λ=1,β=0.01,p=1.5,q=0.1. From Figure 2 it can be observed that the solutions increase with time and will blow up when four different initial values are chosen. Specifically, the solutionsu1,u2,u3andu4grow slowly whent∈(0,150], and rapidly grow to infinity at their corresponding time. It also can be seen that the blowup time ofu4is the shortest.

Figure 1: G1

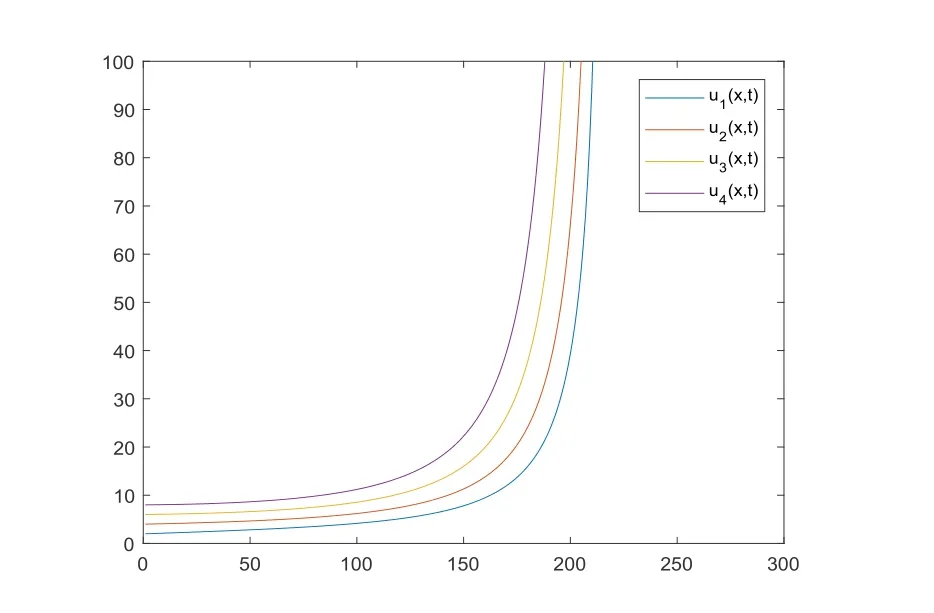
Figure 2: the blowup phenomenon of the numerical solution to problem (1.1)

5 Conclusion

In this article,we first use the Banach fixed point theorem to prove the local existence of the solution.Then the upper and lower solution method is used to prove that the solution is global solution under certain conditions. When the solution is the global solution and when the blowup phenomenon occurs are discussed and the estimation of the blowup rate is given. Finally,we use the explicit finite difference method to simulate the problem(1.1),and the results show that the solution of problem(1.1)indeed blows up. We only discuss the Dirichlet boundary conditions in this paper,and it will be more interesting to extend it to Neumann boundary conditions in the future.

Acknowledgments

The authors are very grateful to the editors and reviewers for their constructive comments.