Dynamics for Three Dimensional Generalized Navier-Stokes Equations with Delay

LU Rui,GUO Chunxiao,*,YANG Xin-Guang and ZHANG Pan

1 Department of Mathematics,China University of Mining and Technology Beijing,Beijing 10083,China.

2 Department of Mathematics and Information Science, Henan Normal University,Xinxiang 453007,China.

3 College of Mathematics and Statistics,North China University of Water Resources and Electric Power,Zhengzhou 450011,China.

Abstract. This paper is concerned with the existence of pullback attractors for three dimensional generalized Navier-Stokes equations with delay. According to compact argument,the existence and uniqueness of weak solutions are proved by using Galerkin method, and the continuous dependence of solutions on initial values is also shown.Based on the asymptotic compactness via weak convergence method and pullback absorbing set on appropriate functional phase spaces, we get the existence of pullback attractors.

Key Words: Three dimensional generalized Navier-Stokes equations;delay;pullback attractor.

1 Introduction

As early as the end of the 18th century, it has been found that the change rule of many things is not only dependent on the current state,but also related to the historical state.In this case,we need to consider the influence of time delay. Later on,the delay differential equation is used to describe the development system that depends on both the current state and the past state.Its characteristic is to fully consider the influence of the history of the system on status quo. Its general form is functional differential equation,which has been studied for more than 200 years. In 1771,Condorcet[1]derived the first functional differential equation in history, but the systematic research work did not really appear until the 1950s. By the 1970s,the research on delay differential equation theory has been developed greatly. Important achievements have been made in many aspects such as the basic theory of solution and stability theory, etc., see literature [1-7], among which the reference [3] is a good summary of the bounded delay functional differential equation research. Moreover,the delay differential equation can be applied to many practical problems, such as studying the law of single population growth, ship stability control,etc.,which has important research significance.

The study of Navier-Stokes equations is important for understanding fluid turbulence and can generally be used to describe the motion of gases and liquids. For a long time,Navier-Stokes equations have been concerned and studied by many scholars such as Ladyzhenskaya,Temam,Robinson,Caraballo,Real and so on. For their related articles and books,see references[8-17]. There are also many studies on the Navier-Stokes equations with time delay terms. The first one was initiated by Caraballo and Real[15]and many important results were obtained[18-22]. Among them,the references[18,19,21]studied the two-dimensional Navier-Stokes equations with time delay, while literature [20,22]studied the three-dimensional modified Navier-Stokes equations with time delay.

For the classical three-dimensional Navier-Stokes equation,the uniqueness of its weak solution is unknown,which makes it difficult to study its asymptotic behavior. Lions[23]and Prodi[24]studied the existence and uniqueness of weak solutions for three-dimensional Navier-Stokes equations with nonlinear viscosity. Caraballo and Real [16] gave a general theorem for the existence and uniqueness of solutions of two-dimensional Navier-Stokes equations with time delays and for the existence of solutions in threedimensional cases. Caraballo and Han [25] studied stability of stationary solutions to 2D-Navier-Stokes models with delays. Quyet [26] studied the existence of pullback attractor for two-dimensional g-Navier-Stokes equations with infinite delay.Caraballo and Han [27] studied the existence, uniqueness and asymptotic properties of solutions of Navier-Stokes models with time delays. The results of the existence and upper semicontinuity of the attractor for time-delay equations can be referred to[28-32]. Yang and his collaborators studied the structure and stability of the pullback attractor for the threedimensional Brinkman-Forchheimer equation with time delay in [33]. As for the existence results of the attractor for time-delay equations can be referred to[34-37],in which the studies on random time-delay equations are mainly referred to[35-37]. However,as our best knowledge,there is less results for the well-posedness and pullback dynamics for three dimensional incompressible generalized Navier-Stokes equations, which attracts our attention.

This paper is concerned with the pullback dynamics for the following three-dimensional generalized Navier-Stokes equations with time delay,which reads as

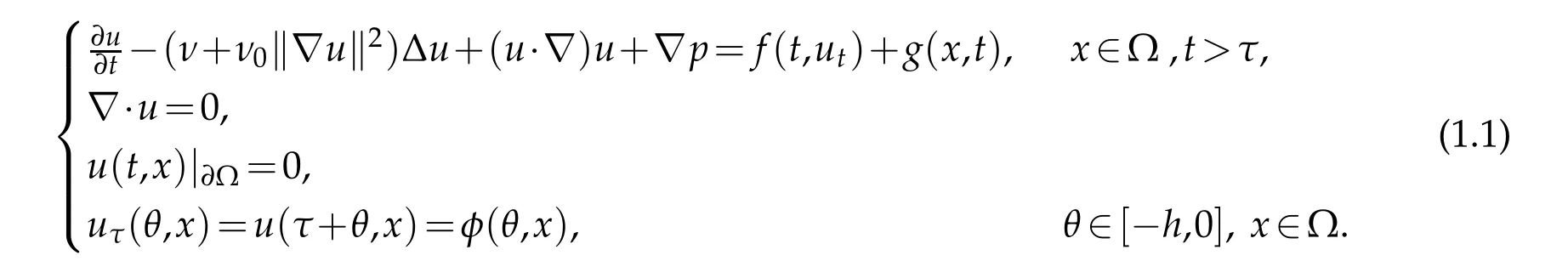
where Ω is a bounded domain of R3with smooth boundary∂Ω andv,v0＞0,pis the pressure.f(t,ut) is the delay term,g(x,t) is the external force, which satisfy the appropriate assumptions respectively.The functionφ(θ,x)is the initial value on[-h,0],whereφ(0,x)=φ(x)=u(t=τ,x),τ∈R,ut(θ)=u(t+θ),θ∈[-h,0],h＞0.

The main features and results of this paper can be summarized as follows:

(I)By virtue of the Fadeo-Galerkin technique and compact argument,the existence of global weak solution can be shown. Originated by Ball in 2004, we can use the energy equation approach to achieve the pullback asymptotic compactness, which leads to the pullback attractors together with some dissipation of our problem.

(II)Comparing with the classical three-dimensional Navier-Stokes equations,the uniqueness of its weak solution for classical case is unknown.However,the weak solution of Eq.(1.1)is unique,see references[23,24]. Hence,Eq.(1.1)is well-posed and can generate a dynamical system.

(III)The upper semi-continuity of pullback attractors for problem(1.1)with perturbed delay will be proved in appropriate phase spaces in future.

In this paper,we first prove the existence,uniqueness and continuous dependence of the solution of Eq.(1.1) on the initial value. Then we continue to prove the existence of pullback attractors, and finally discuss the relationship between these families of pullback attractors for Eq.(1.1)based on different universes.

2 Preliminaries

2.1 Some functional spaces.

Define a function space of smooth functions

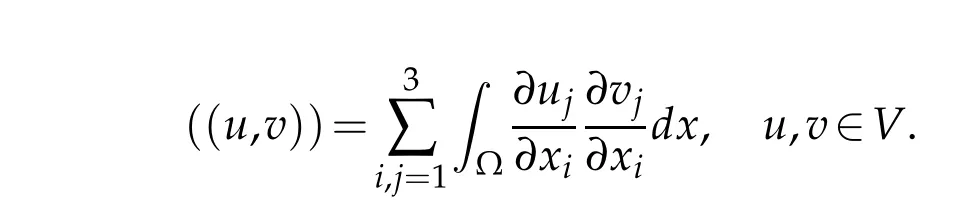
are referred to references[12,14],and will not be reviewed here.

2.2 Functional Banach spaces.

Some useful functional Banach spaces are defined by

2.3 The theory of pullback attractors.

LetXbe a complete metric space, ˆDis a family of non-empty sets with respect to the parametert,P(X)be the family of all nonempty subsets ofX,let D be a nonempty class of families parameterized in time ˆD={D(t):t∈R}⊂P(X).

where γ0＞0is a constant.

3 Existence of dynamical systems.

In this section, we prove the existence, uniqueness and continuous dependence of the solution of Eq.(1.1)on the initial value.

3.1 Assumptions.

The following conditions are given for the functionsfandgon Eq.(1.1).

(Hf)The functionf:R×CH→(L2(Ω))3satisfies the following assumptions:

(i)f(t,ξ)∈(L2(Ω))3is measurable,for anyξ∈CH,∀t∈R,

(ii)f(·,0)=0,for anyt∈R,

(iii)f(t,·)is Lipschitz continuous,for anyξ,η∈CH,∀t∈R,i.e.

whereλ1represents the first eigenvalue ofA,Cfis the constant in condition(iv)of(Hf),σandmare constants in(4.4).

3.2 Weak solution and its uniqueness.

Definition 3.1.Suppose f and g satisfy the hypothesis(Hf)and(Hg)respectively, and the function u∈C([τ-h,T];H)∩L2(τ,T;V)∩L4(τ,T;V)is called the weak solution of Eq.(1.1), if for T＞τ,uτ(θ,x)=u(τ+θ,x)=φ(θ,x),θ∈[-h,0]and for any v∈V,the following formula is true almost everywhere on[τ-h,T].

Denote byXn:=span{wj:j=1,2,...,n},thenun(t)∈Xn.un(t) satisfies the following differential equations,for each 1≤j≤n,

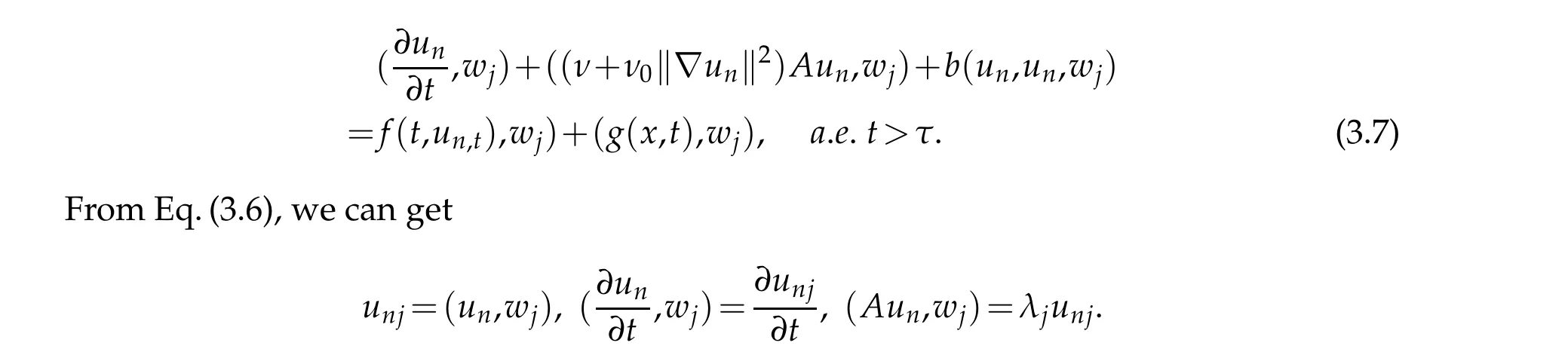
By substituting the above equation into Eq.(3.7),we have

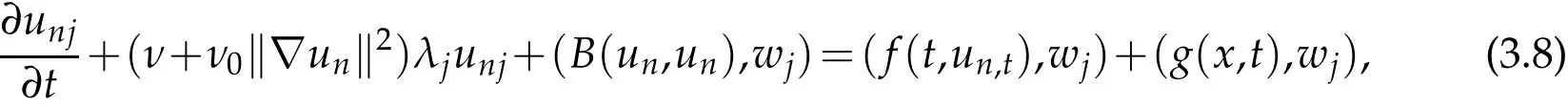
(3.8)can also be written as

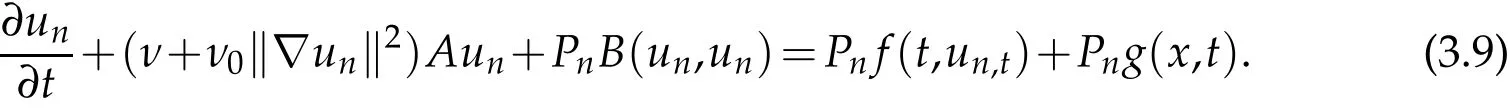
Existence and uniqueness results for ODEs imply that (3.9) have a unique solution for theunj, at least on some short time interval [τ-h,tn),τ＜tn＜∞, and meets the initial conditionsun,τ(θ,x)=un(τ+θ,x)=Pnφ(θ,x),θ∈[-h,0].

Next,the approximate solution of the first step is extended to ensure that the solution is on the interval[τ-h,∞), that is,the solution is global. Letτ＜T＜tnbe fixed. Taking the inner product of(3.9)withunto get

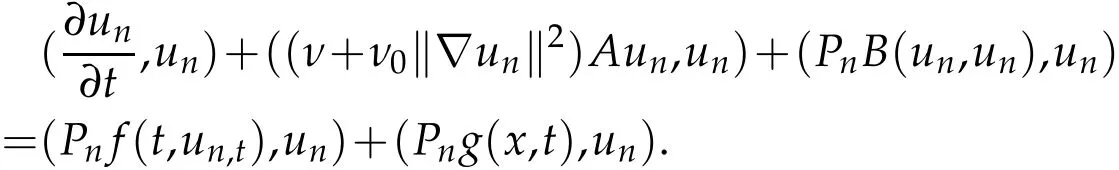
Using the properties of the trilinear operator and the projection operator,the above equation can be written as

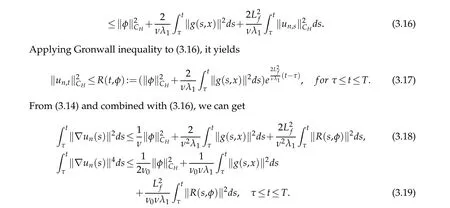
Hence,we obtain that there exists a constantC=C(T,φ)＞0,such that‖un,t‖2CH≤C(T,φ),t∈[τ,T],n≥1.

The proof of the boundedness of each item in Eq.(3.8)follows.

Sinceun,τ(θ,x)=Pnφ(θ,x),θ∈[-h,0], we obtain that the sequenceun(still denoted asun)is bounded inL∞(τ-h,T;H).

Moreover,it follows from(3.14)and(3.17)that the sequenceunis bounded in

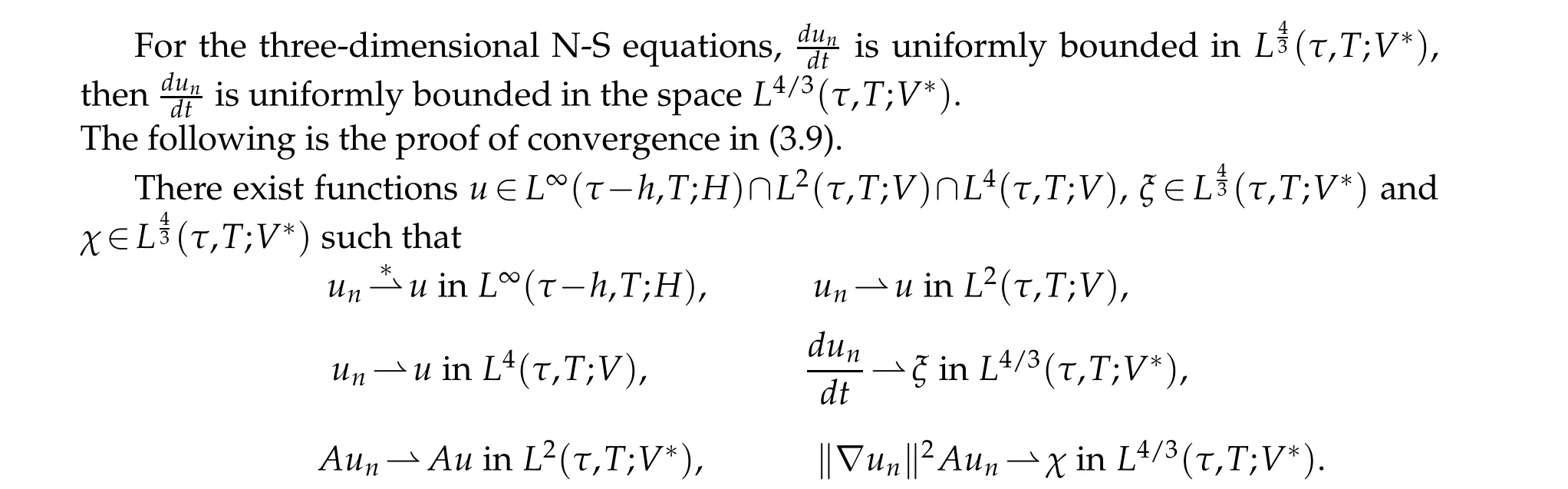
Due to the strong convergence ofunto u inL4(τ,T;H), we get that there exists a subsequence(relabeled asun)such thatunconverges touinHa.e.t∈[τ,T].

Letun(t) andum(t) satisfy approximation Eq.(3.9) and letw(t)=un(t)-um(t), then we have

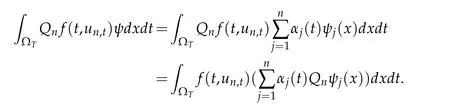
SinceQnψj(x)⇀0 inHfor eachj(See(8.11)in Reference[14]for the proof process),we have the required convergence ofη.

The following proofη=f(t,ut). Because in spaceC([τ-h,T];H),un,t→ut,according to the results of Lemma 8.3 and Corollary 1.12 in Reference [14], it can be known that there is a subsequenceun,t, such thatun,t→utfor almost every (x,t)∈ΩT. It follows,using the continuity off,thatf(t,un,t)→f(t,ut)for almost every(x,t)∈ΩT. Along with the boundedness onf(t,un,t)inL2(τ,T;H),we can apply Lemma 8.3 in reference[14]to deduce thatf(t,un,t)⇀f(t,ut)inL2(τ,T;H). By the uniqueness of weak limits,it follows thatη=f(t,ut). That is,

which shows thatw≡0,i.e.,the solution is unique.

3.3 Continuous dependence on initial data

Theorem 3.2.Assuming that conditions(Hf)and(Hg)hold, the solution of Eq.(1.1)depends continuously on the initial values. More precisely,if ui,i=1,2are the corresponding solutions to the initial conditions φi,i=1,2,then the following estimate holds:

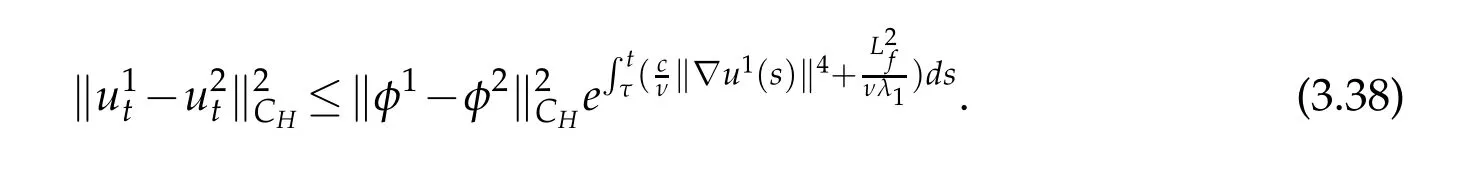
Remark 3.1. According to theorem 3.1 and Theorem 3.2, it follows that there exists unique and continuous solution that depends on initial values. From this,we can define a continuous process,S(t,τ):H×(CH∩L2V)→H×(CH∩L2V),that is,S(t,τ)(φ,φ)=(u,ut).Hence,Eq.(1.1)is well-posed and can generate a dynamical system.

4 Existence of pullback attractors

In this section, we derive uniform estimates and convergence of solution for Eq.(1.1),these estimates are necessary for proving the existence of pullback absorbing set and the asymptotic compactness of the dynamical system.

Lemma 4.1.Assume that (Hf), (Hg) and(H0)hold. Then the solution u of Eq.(1.1)satisfies that,for any K＞0,there exists tK＞0,such that for φ∈CH,‖φ‖CH≤K and∀δ≥tK,the following inequality holds.

Applying H¨older inequality,ε-Young inequality and combining with the properties of the trilinear operator,we have

wherec1,c2andc3is a constant greater than zero.

By substituting the above inequality into(4.15),we get

From the continuity and boundedness off,

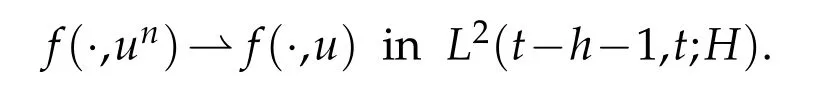
From the convergence of the above terms, it can be concluded thatu∈C([t-h-1,t];H)is the weak solution of Eq.(1.1), and the initial value ofuat the initial timet-h-1 is denoted asut-h-1.

From Lemma 4.3,we know thatunis bounded inL∞(t-h-1,t;V),dun/dtis uniform bounded inL43(t-h-1,t;V*),using the Aubin-Lions-Simon Lemma,we can derive that

Then the functionsIn(s) andI(s) are continuous and non-increasing on[t-h-1,t], and it can be obtained that

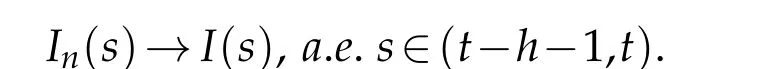
So for anyε＞0,∃nk∈N,for anyn≥nk,∃{sk}⊂[t-h-1,t],such that ask→∞,sk→s,and

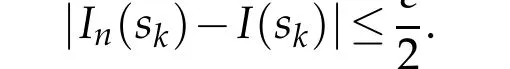
SinceI(s)is continuous,then for anyε＞0,there exists ˜nk∈N,such that for ∀n≥˜nk,the sequencesk→s,and there is

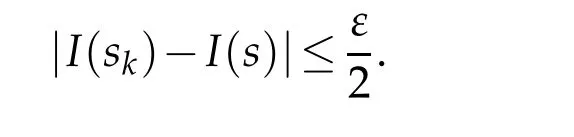
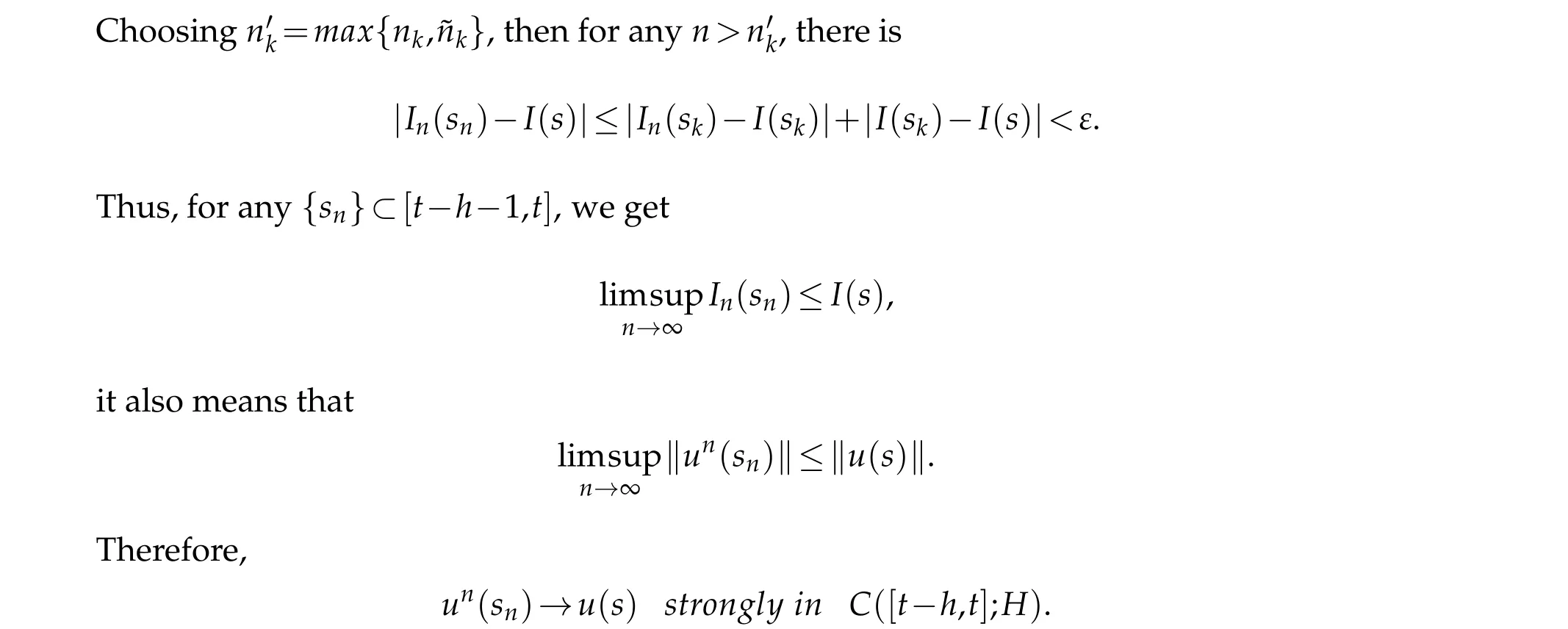
Combined with the above energy estimates,by using the continuity of the defined functionsI(s)andIn(s)and the convergence ofun,it can be concluded that

5 Further research

This paper has investigated the existence of pullback attractors for three dimensional generalized Navier-Stokes equations with time delay inMHspace. The upper semicontinuity of the pullback attractor for Eq.(1.1)is also worth studying in future.

Acknowledgement

The authors are grateful to the referees for their helpful suggestions which improved the presentation of this paper. Chunxiao Guo was partially supported by NSFC of China(Grant 11771444), the Yue Qi Young Scholar Project, China University of Mining and Technology (Beijing). Xin-Guang Yang was partially supported by the Fund of Young Backbone Teachers in Henan Province (No. 2018GGJS039) and Incubation Fund Project of Henan Normal University(No. 2020PL17).