Exact Boundary Controllability of Fifth-order KdV Equation Posed on the Periodic Domain
YANG Shuning and ZHAO Xiangqing
1 School of Information and Engineering,Zhejiang Ocean University,Zhoushan 316022,China.
2 Department of Mathmatics,Suqian University,Suqian 223800,China.
Abstract. In this paper, we show by Hilbert Uniqueness Method that the boundary value problem of fifth-order KdV equation
Key Words: Fifth-order KdV equation;Hilbert Uniqueness Method;exact controllability.
1 Introduction
In[1,2],the authors have studied the internal controllability of the fifth-order Kortewegde Vries equation posed on a periodic

one can find a control input h∈L2(0,T;Hs(T))such that the system(1.1)admits a solution u∈C(0,T;Hs(T))satisfying

Naturally, we will ask the question that how about boundary controllability of the system.Specifically,is the following system

and that the Sobolev norm
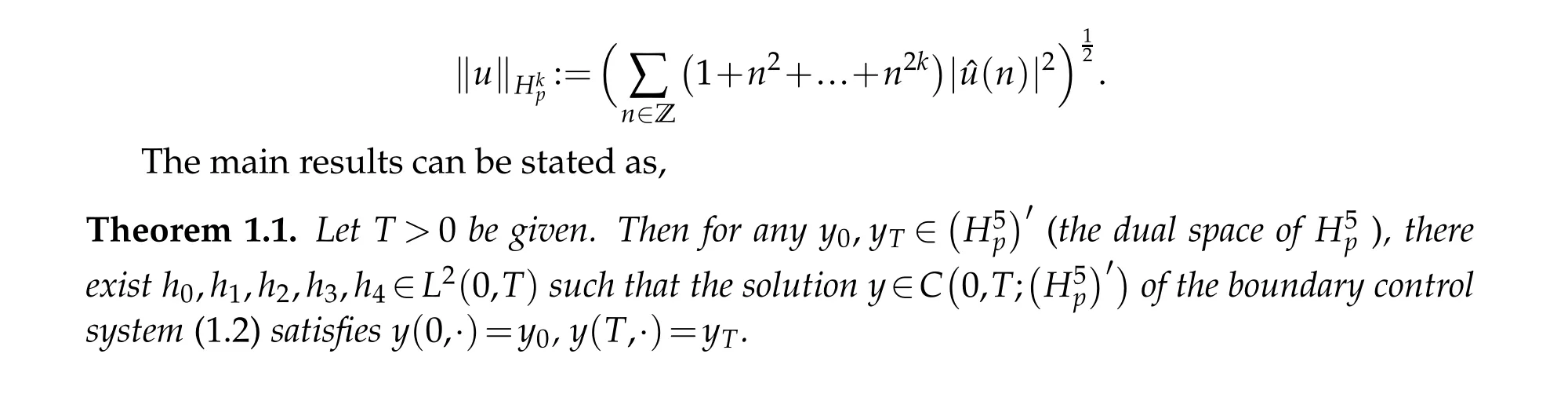
2 Observability inequality
As is well-known,the controllability of the original system is equivalent to the observability of its adjoint system. As preparation for the Hilbert Uniqueness Method argument,we'll establish the critical identity and observability inequality in this section.
2.1 Adjoint system
Firstly,we show the representation of the solution for the adjoint system

2.2 Observability inequality
With the explicit solution(2.2)of adjoint system in hand,we can establish the observability inequality:

We get the left inequality in the general case by a density argument.
2.3 Existence of solution

In order to show the existence of solution to After this transformation,the existence of solution of(2.5)is classic results of semi-group theory.
2.4 Critical Identity
Combine(2.1)and(2.5),we establish the critical identity.


where[x]denotes the integral part of a real numberx.
3) IdentifyingL2(0,2π) with its dual by means of the (conjugate linear) mappingy(·,y)L2(0,2π),we have the following diagram:

where each embedding is dense and compact. Moreover

is a continuous linear form. On the other hand the map
is clearly an automorphism of Hilbert space. Hence for eachS∈[0,T],y(S) is uniquely defined in(H4p)'. Moreover forS∈[0,T],
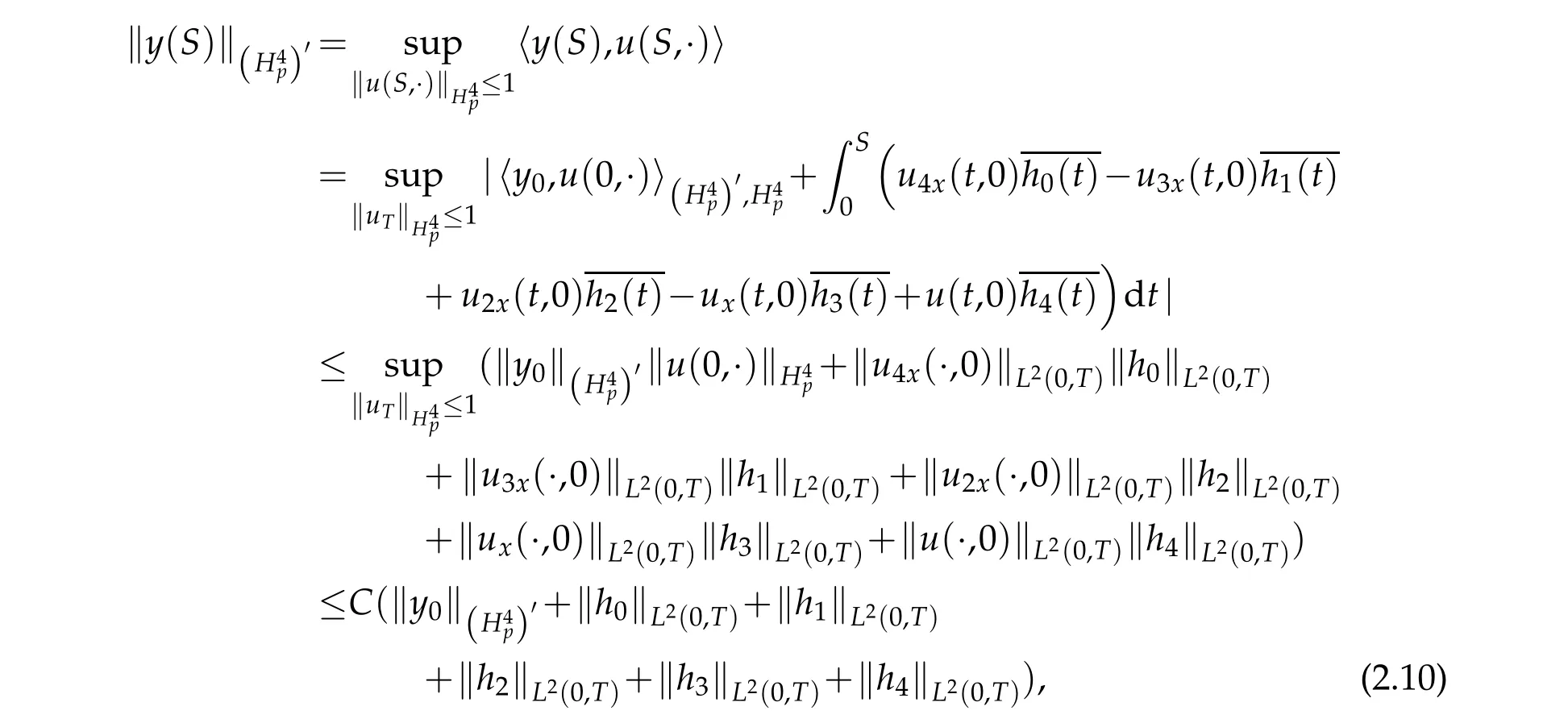
whereCis a positive constant which does not depend onSor ony0,h0,h1,h2,h3,h4. Since
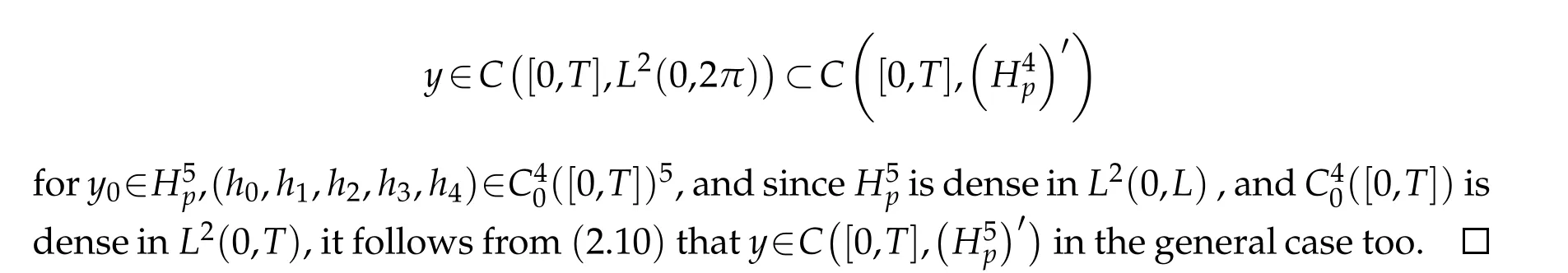
3 HUM argument
We complete the proof of Theorem 1.1. by applying Hilbert Uniqueness Method argument.
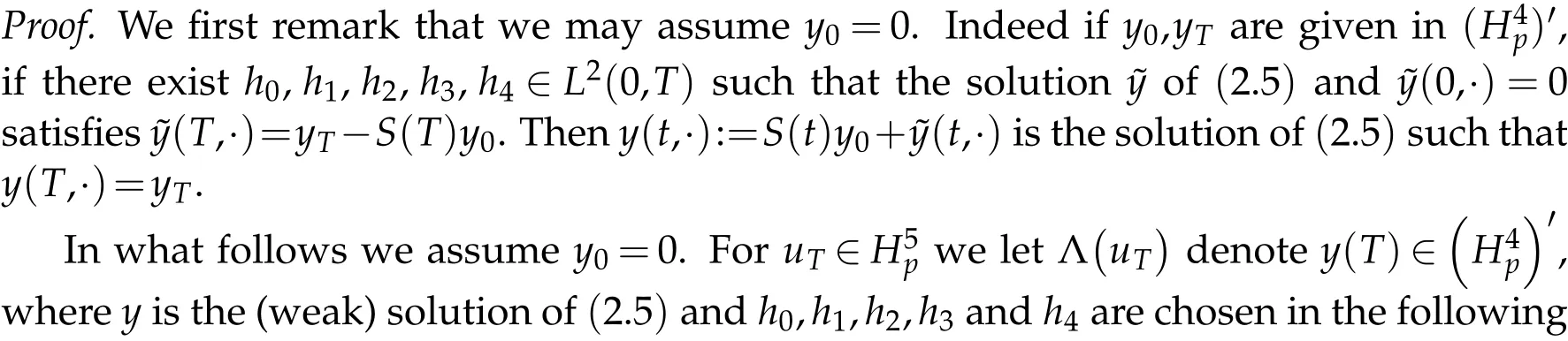

It follows from Lax-Milgram theorem that Λ is invertible. Thus, the system is exact controllable.
4 Concluding remarks
Remark 4.1. (i)IfT=2πthe observability result is obvious. Indeed,for anyuT∈H4p

Remark 4.2.Progress on the internal controllability on the fifth-order Korteweg-de Vries equation have made in the past(see[1,2,7])following the step of that of classic Kortewegde Vries equation.However,for the boundary controllability on the fifth-order Kortewegde Vries equation,there is still a long way to go.
Acknowledgement
This work is financially supported by the Zhejiang Provincial Natural Science Foundation of China(No.LY18A010024)and National Natural Science Foundation of China(No.12075208).
 Journal of Partial Differential Equations2022年2期
Journal of Partial Differential Equations2022年2期
- Journal of Partial Differential Equations的其它文章
- Global Existence and Time-decay Rates of Solutions to 2D Magneto-micropolar Fluid Equations with Partial Viscosity
- Blowup Behavior of Solutions to an ω-diffusion Equation on the Graph
- Dynamics for Three Dimensional Generalized Navier-Stokes Equations with Delay
- The Obstacle Problem For Nonlinear Degenerate Elliptic Equations with Variable Exponents and L1-Data
