The Obstacle Problem For Nonlinear Degenerate Elliptic Equations with Variable Exponents and L1-Data

KHELIFI Hichem

Department of Mathematics,University of Algiers,Algeria.2 Street Didouche Mourad Algiers. Laboratory LEDPNL,HM,ENS-Kouba,Algeria.

Abstract. The aim of this paper is to study the obstacle problem associated with an elliptic operator having degenerate coercivity, and L1-data. The functional setting involves Lebesgue-Sobolev spaces with variable exponents. We prove the existence of an entropy solution and show its continuous dependence on the L1-data in W1,q(·)(Ω)with some q(·)＞1.

Key Words: Ostacle problem; Degenerate Coercivity; Variable exponents; L1 data; Truncation function.

1 Introduction

Let Ω⊂RN(N≥2)be a bounded domain with smooth boundary∂Ω. andf∈L1(Ω). We consider the following nonlinear problem

whereAthe operateur define by

Equations with variable exponents appear in various mathematical models. In some cases,they provide realistic models for the study of natural phenomena in electro-rheological fluids and important applications are related to image processing. We refer the reader to[3,4].

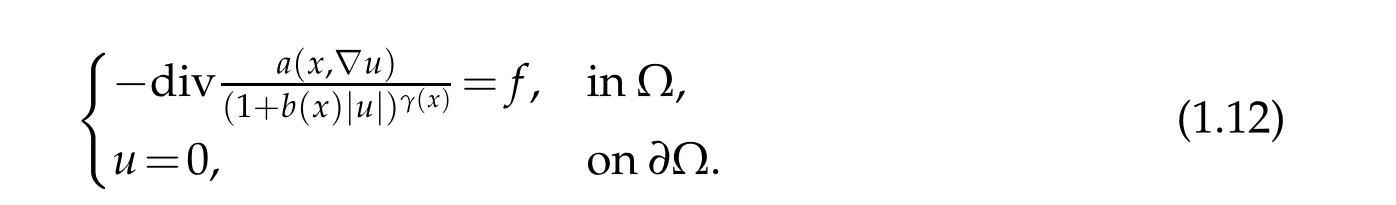
The motivation of this paper comes from the study the following nonlinear elliptic problem When the degenerate term does not appear in (1.12) (i.e.,γ(x)=0), anda(x,∇u)=|∇u|p(x)-2∇u, the existence and uniqueness of entropy solutions of (1.12) are proved in [5]. Ifγ(x)=θ(p(x)-1), withθ≥0 anda(x,∇u)=|∇u|p(x)-2∇uthe problem (1.12),have been treated in[6],under the hypothesisf∈Lm(.)(Ω),withm(x)≥m-≥1, the authors as showed the existence and regularity results for the solutions.

In the classical casep(x)=pandγ(x)=θ(p-1), with 0 ＜θ≤1 andf∈L1(Ω), the existence and regularity of solutions to problem(1.1) are proved in[7,8] and [9-13], respectively.The corresponding resultsf∈Lm(Ω)(m＞1)have been developed in[7,14,15].

The second difficulty appears when we give a variable exponential growth condition(1.7) fora. The operatorApossesses more complicated nonlinearities; thus, some techniques used in the constant exponent case cannot be carried out for the variable exponent case.

The following theorem is the main result obtained in this paper.

Theorem 1.1.Let f∈L1(Ω). Assume that(1.3)-(1.9)hold. Then there exists at least one entropy solution u of the obstacle problem associated with(f,ψ,g). In addition, u depends continuously on f,i.e.,if fn→f in L1(Ω)and un is a solution to the obstacle problem associated with(fn,ψ,g),then

2 Mathematical preliminaries

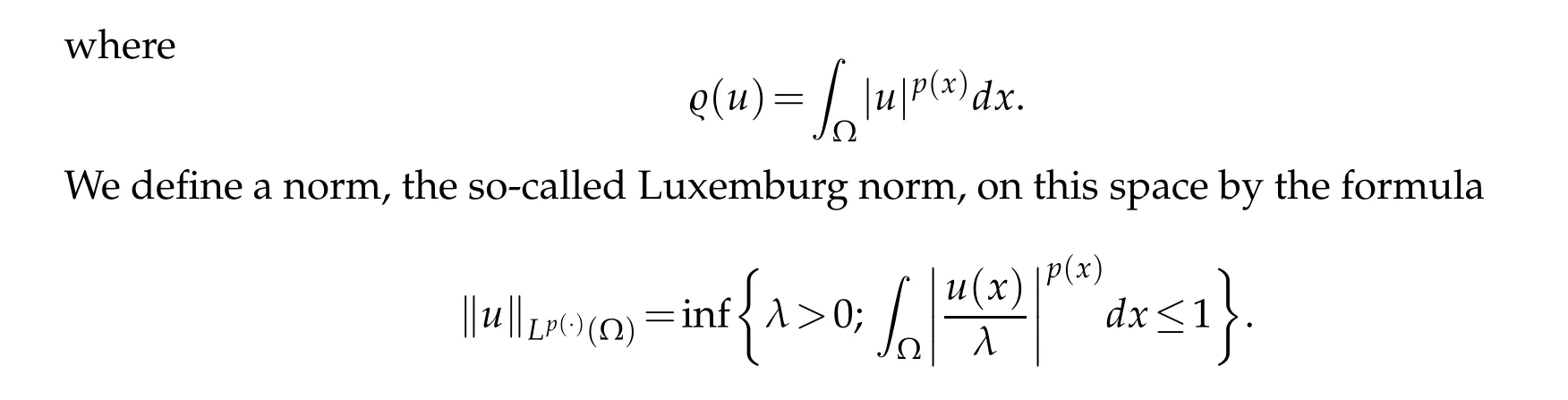
The following Lemma will be used later.

Lemma 2.1.If un,u∈Lp(·)(Ω)and p+＜+∞,then the following properties hold true:

Remark 2.1. Note that generalized Lebesgue and Lebesgue-Sobolev spaces can also be defined in the same way for only measurable real-valued variable exponentsp(·)satisfying 1＜pinf≤psup＜∞,wherepinf=ess-infx∈Ωp(x),psup=ess-supx∈Ωp(x). According to [21], such variable exponent Lebesgue spaces are Banach spaces, the H¨older-type inequality holds,they are reflexive if and only if 1＜pinf≤psup＜∞. The inclusion between Lebesgue spaces also generalizes naturally: if 0＜|Ω|＜∞andr1,r2are variable exponents so thatr1(·)≤r2(·)almost everywhere in Ω then there exists the continuous embeddingLr2(·)(Ω)Lr2(·)(Ω),whose norm does not exceed|Ω|+1.

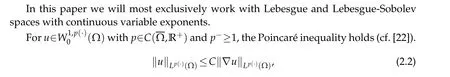
for some universal constantCwhich depends on Ω and the functionp.

3 Lemmas on entropy solutions

In the remainder of this section,we denote byCi,i=0,1,2,3,...various positive constants depending only on the data of the problem,but not onnandk.

It is worth noting that, for any functionfnsmooth enough, there exists at least one solution to the obstacle problem(1.10). Indeed,we can proceed exactly as in Lemma 3.1.of[6] to obtainW1,p(·)-solutions due to assumptions(1.3)-(1.9), which, particularly, are also entropy solutions. In this section, we establish several auxiliary results on convergence of sequences of entropy solutions asfn→finL1(Ω).

Lemma 3.1.Assume(1.3)-(1.9)and let v0∈Kg,ψ∩L∞(Ω). If u is an entropy solution to the obstacle problem associated with(f,ψ,g). Then

for allt＞0. On the other hand,using assumptions(1.6),(1.7)and Young's inequality withε＞0,we have,for allt＞0,

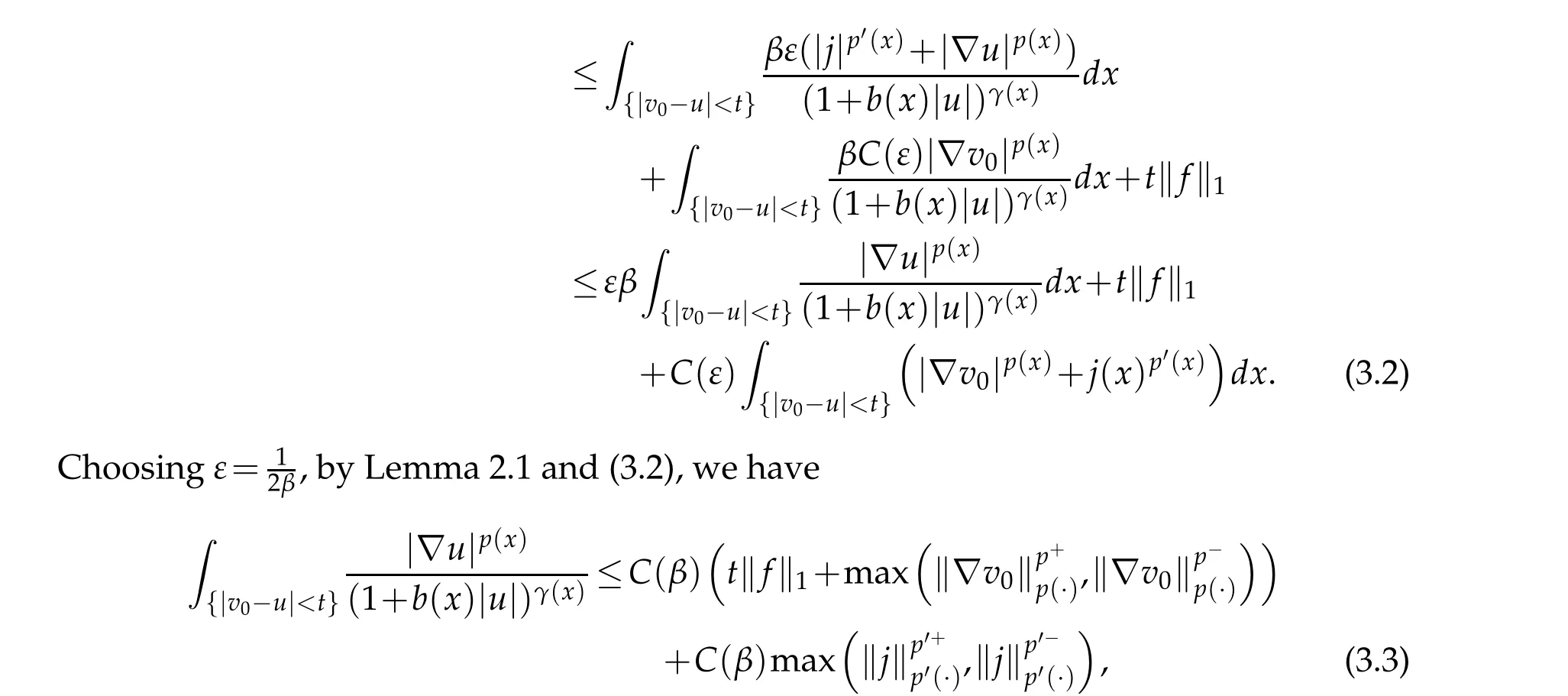
for allt＞0. Replacingtwitht+‖v0‖∞in (3.3) and noting that {|u|＜t}⊂{|v0-u|＜t+‖v0‖∞},we obtain(3.1)for allt＞0.

Remark 3.1. Notice that estimate(3.1)implies that

In the rest of this section,let{un} be a sequence of entropy solutions to the obstacle problem associated with(fn,ψ,g)and assume that

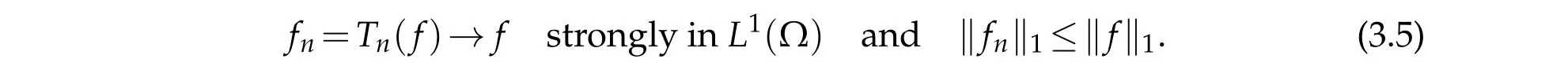
Lemma 3.2.Assume(1.3)-(1.9). For k＞0large enough, there exists a measurable function u such that un→u in measure and Tk(un)⇀Tk(u)weakly in W1,p(·)(Ω). Thus Tk(un)→Tk(u)strongly in Lp(·)(Ω),and up to a subsequence,Tk(un)→Tk(u)a.e. inΩ.

Proof.Lets,t,andεbe positive numbers. Noting that

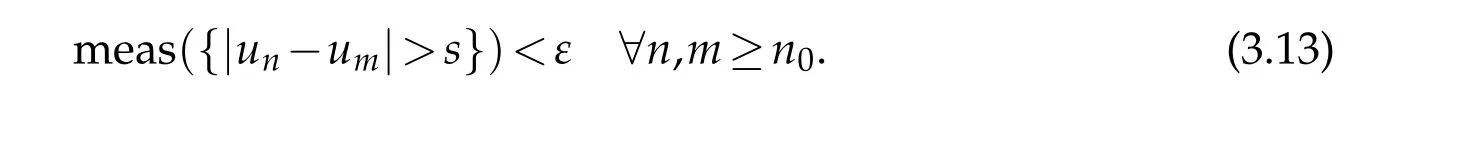
Combining(3.6),(3.10),and(3.12),we obtain Hence {un} is a Cauchy sequence in measure, and therefore there exists a measurable functionusuch thatun→uin measure. Note thatTk(un)-Tk(g)∈W1,p(·)0(Ω). By (3.8)and Poincar´e's inequality (see (2.2)) we conclude that, for fixedk, {Tk(un)} is a bounded sequence inW1,p(·)(Ω). Therefore,Tk(un)→Tk(u) strongly inLp(·)(Ω), and, up to a subsequence,Tk(un)→Tk(u)a.e. in Ω.

Lemma 3.3.Assume(1.3)-(1.9)and let p(·),γ(·)as in Theorem1.1. There exists a subsequence of{un}and a measurable function u such that for each q(·)given in(1.14)we have un⇀u weakly in W1,q(·)(Ω),and un→u strongly in Lq(·)(Ω).

Proof.Letk＞0 andn≥1. DefineAk={|un|≤k}andBk={k≤|un|＜k+1}. Using Lemma 3.1 and(3.1)withv0=g+(ψ-g)+,we get

To estimate the first integral in the right-hand side of (3.23), using H¨older's inequality,(3.14),and(1.5),we obtain

Putting together all the limitations and noting that I(n),and using(3.39)-(3.42),we have

4 Proof of the main result

Now we have gathered all the lemmas needed to prove the existence of an entropy solution to the obstacle problem associated with(f,ψ,g). In this section,letfnbe a sequence of smooth functions converging strongly tofinL1(Ω)with‖fn‖1≤‖f‖1+1. We consider the sequence of approximated obstacle problems associated with(fn,ψ,g).

Note that we have meas({|v-u|=t})=0 for a.e.t∈(0,∞). So there exists a measurable set O⊂(0,∞)such that meas({|v-u|=t})=0 for allt∈(0,∞)O. Assume thatt∈(0,∞)O.Thenχnconverges weakly*inL∞(Ω) and a.e. in Ω toχ=χ{|v-u|＜t}. Since ∇Ts(un)converges a.e. to ∇Ts(u)in Ω(see Corollary 3.1),by Fatou's lemma we obtain

Hence,uis an entropy solution of the obstacle problem associated with (f,ψ,g). The regularity of the entropy solutionuis guaranteed by Corollary 3.1.