力学超材料柔性后缘设计技术
熊继源,戴宁,叶世伟,郭培,程基彬
南京航空航天大学,江苏 南京 210016
变形机翼是通过改变机翼弦长、面积、后掠角等方式,实现机翼结构的连续变化来优化飞行性能,其中变后缘弯度作为能够有效提高机翼气动性能的方法,在新一代飞行器设计中受到广泛关注[1]。目前由传统机械结构构成的可变后缘弯度机翼已取得诸多成果,Pecora 等[2]通过刚性组件的运动实现襟翼的连续变形,完成了等比大小机翼实物制造及试验。Zhao 等[3]提出了一种通过双肋板直接接触传递载荷的多铰链结构变弯度机翼,结果证明其飞行效率比传统固定翼飞行效率提高14.1%。仿生也为机翼结构设计带来了新的思路,Woods 等[4]提出类鱼骨式仿生微结构布局的可变形机翼结构,在此基础上,李扬[5]提出了一种基于几何非线性的链式梁约束模型的鱼骨结构大变形理论模型,采用气动肌肉驱动鱼骨形柔性肋完成机翼后缘的柔性变形。
在以智能材料为主要结构的柔性后缘研究中,以形状记忆合金(SMA)的应用最为广泛,Gu 等[6]将形状记忆合金嵌入基础结构中作为驱动器实现机翼形状的精准控制。Anna 等[7]基于SMA 设计的柔性后缘,其偏转角最大可达到102°。欧盟采用形状记忆合金和压电驱动器相结合的方法于2020年在A320机翼上进行全尺寸翼段试验[8]。
力学超材料技术作为近年来智能材料领域的研究热点,因其具备不同于天然材料的超常物理性质而受到了人们的广泛关注[9],通过人工设计的力学超材料结构能够在载荷的作用下呈现正泊松比、负泊松比、零泊松比与扭转等不同的力学性能[10-13]。2008 年,Spadoni 等[14]选用手性力学超材料结构设计填充机翼内部,使机翼具有独特的变形特性。2016年,麻省理工学院(MIT)与美国国家航空航天局(NASA)合作提出基于两种不同特性超材料的模块化扭转机翼,在实现机翼连续扭转变形的前提下极大提高了其制造、维护效率[15]。2019 年,MIT 与NASA 进一步合作,仅使用一种超材料结构作为构建单元,组装完成了翼展为4.27m 的机翼并进行了风洞试验[16]。刘凯等[17]总结了国内外手性力学超材料在可变形机翼设计上的研究进展,为我国可变形飞机机翼的设计提供了参考。Boston等[18]将设计的力学超材料结构填充进NACA0012翼型中,当6节超材料结构完全展开时,机翼翼展增加了0.08m,升力提高了21%。
本文研究基于力学超材料的柔性可变后缘弯度机翼的基本原理,设计并制备出具有不同力学特性的二维微结构单元,而后采用组装方法将其装配具有典型力学性能的三维超材料微结构胞元,在仿真结果的基础上完成机翼结构的整体设计,并通过增材制造技术完成机翼实物的制造、装配及性能测试。
1 柔性后缘设计方案
1.1 技术路线
设计力学超材料单元时要考虑柔性后缘结构的变形、承载、驱动控制等要求,保证结构在稳定的同时产生较大的弯曲变形。针对这些需求,本文对基础翼型进行分析并建立有限元模型,针对目标襟翼柔性变形的要求,选用具有高弹性的零泊松比力学超材料为主体设计后缘变形结构,选用刚性较好的正泊松比结构作为增强结构以保证机翼后缘的承载能力。采用离散装配技术制备结构可替换的三维力学材料胞元,根据机翼弦长及变形目标填充力学超材料胞元,完成机翼结构的整体设计,并通过仿真和实物试验对其驱动控制和变形能力进行研究。柔性后缘设计优化流程如图1所示。
1.2 柔性后缘气动模型优化
本文选用NACA4418 作为可变后缘机翼的基础翼型,NACA4418 襟翼变化如图2 所示,定义转轴点到后缘的连线与初始翼型弦线间的夹角为后缘偏转角θ,向下偏转时为正。在马赫数、雷诺数相同的情况下对后缘偏转角θ及其气动性能进行数值研究,图3 为后缘偏转角θ=7°时的升阻比CL/CD随迎角α的变化曲线,可以看出机翼的升阻比均随着迎角的增加先升高后降低,其中变后缘机翼的升阻比在迎角为3°时达到59.79,在迎角为-8°~7°时,变后缘机翼升阻比明显优于初始翼型。图4 为后缘偏转角θ=15°时的压力系数变化,从整体上来看,变后缘机翼上下表面压力系数所围成的面积大于初始翼型压力系数所围成的面积,表现为变后缘机翼的升力系数大于初始翼型,证明变形后翼型相比未变形翼型具有更好的气动性能。

图2 NACA4418翼型后缘变化示意图Fig.2 NACA4418 airfoil trailing edge variation diagram

图3 基本翼型与变后缘翼型升阻比曲线Fig.3 Lift-drag ratio curves of basic airfoil and variable trailing edge airfoil
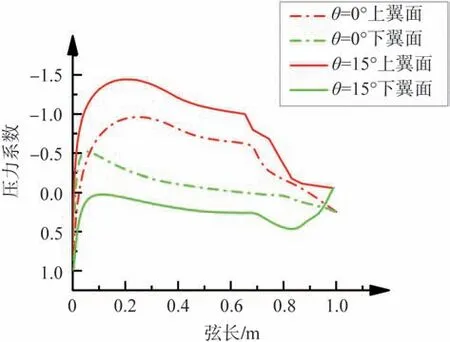
图4 基本翼型与变后缘翼型压力系数分布Fig.4 Pressure coefficient distribution of basic airfoil and variable trailing edge airfoil
1.3 柔性后缘变形原理
本文设计的机翼结构由两部分组成:一是可变形结构,其主要包括柔性后缘结构和可变性蒙皮;二是不可变形结构,主要包括主体刚性填充结构及翼肋等主要支撑结构。主体刚性填充结构由多个三维正泊松比胞元连接构成,并依照机翼弦长与胞元最小尺寸进行最密排布,如图5所示红色胞元部分。考虑到变后缘的需求,选取零泊松比结构组成复合胞元进行后缘结构设计,如图5所示绿色胞元部分。

图5 变后缘机翼结构示意图Fig.5 Schematic diagram of variant trailing edge wing structure
主要驱动方式采用单索传动机构,如图6所示,将绳索的一端与后缘混合胞元固定,另一端通过定滑轮与驱动器相连,当驱动器带动绳索产生收缩位移时,混合胞元在载荷作用力F下发生弯曲变形,通过连接结构使蒙皮发生形变,完成机翼后缘的弯曲。当驱动位移为0时,由于零泊松比单元自身结构及蒙皮弹力的作用,机翼后缘重新恢复初始形状。
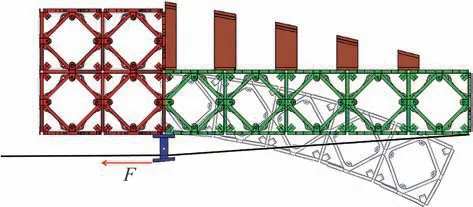
图6 柔性后缘变形原理Fig.6 Deformation principle of flexible trailing edge
2 柔性后缘结构设计
2.1 力学超材料单元结构设计
由于力学超材料的力学特性与变形方式主要取决于胞元结构,因此本文以两种二维超材料单元结构为基础,通过离散装配构建三维力学超材料胞元,调配二维结构参数及单元数量实现三维结构功能性设计。
本文选用空间利用率高的正方几何结构为基础进行二维正泊松比单元结构设计,二维正泊松比结构及其几何参数如图7(a)所示,二维零泊松比单元是在前述正泊松比单元基础上,将刚性杆件结构替换为柔性杆件,其特征为折叠弯曲的柔性杆状结构,如图7(b)所示。

图7 二维单元结构示意图Fig.7 Schematic diagram of two-dimensional element structure
在评估单元结构效率时,可以通过二维结构的相对密度ρ更好地体现结构差异,如式(1)所示,其二维结构的相对密度可以通过结构物理面积A*(单元物理材料占据面积)与实际二维单元占据总面积AS(单元包围盒面积)之比进行表征

考虑到机翼尺寸、实际制造工艺及单元连接,为制造适合人工快速装配的最小单元结构,本文选用表1 中的单元参数做进一步研究。

表1 二维单元几何参数Table 1 Two-dimensional element geometric parameters
为验证二维结构力学性能,本文采用ABAQUS软件对其进行仿真数值分析。单元结构材料采用PA12,其弹性模量为1200MPa,密度为1.26g/cm3。通过对单元的一个连接处施加固定约束,对角连接处施加位移边界条件,考虑到单元整体对称,简化为对一个方向进行测试验证便可得到对应垂直方向上的力学性能。为了更好地评估结构效率,以结构整体的应力应变为基础,并引入单元相对密度,得出单元结构模量计算表达式如下。

图8所示为改变杆径条件下的单元结构弹性模量的变化结果,可以看出,随着杆径的增加,单元结构弹性模量也在随之增加,在相同杆径下,即使正泊松比结构的相对密度要远小于零泊松比结构,其单元结构弹性模量也能明显大于零泊松比结构,当杆径为2.5mm 时,正泊松比单元的结构弹性模量约为零泊松比单元的3.4倍,体现其良好的承载性能。
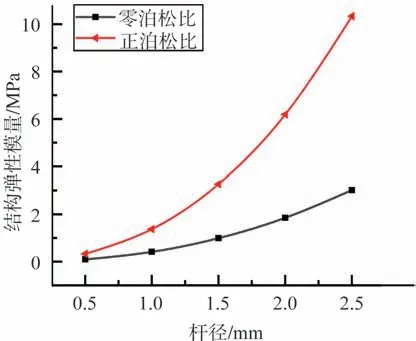
图8 杆径对结构杨氏模量的影响Fig.8 Influence of rod diameter on elasticity modulus of structure
对于零泊松比结构来说,决定其泊松比性能的两个主要因素为曲杆内凹长度L1与连接倒角RQ2,图9与图10为对应结构参数变化对结构泊松比的影响,从结果可以看出,随着连接倒角RQ2与曲杆内凹长度L1的增大,单元泊松比逐渐降低。

图9 连接倒角RQ2对泊松比的影响Fig.9 Influence of connection chamfer RQ2 on Poisson’s ratio

图10 内凹长度L1对泊松比的影响Fig.10 Influence of concave length L1 on Poisson’s ratio
2.2 柔性后缘简化建模
在确定二维结构的各项参数之后,就可通过离散装配完成三维胞元的设计,图11 为三维胞元的拼接方法,在每个二维单元的连接处存在与二维单元平面成45°夹角的连接孔,将二维单元按连接孔两两贴合后,通过螺栓可以固定每个二维单元间的位置。柔性后缘结构主要由混合胞元构成,单个混合胞元由2片零泊松比单元及4片正泊松比单元组装构成,图12为混合胞元受到平面正向载荷的变形示意图,其中正泊松比单元能够提供足够的刚性,而零泊松比单元能够保证在变形的同时,垂直于载荷方向不发生形变,保证柔性后缘结构不发生额外的形变。

图11 三维胞元装配方法Fig.11 Three dimensional cell assembly method
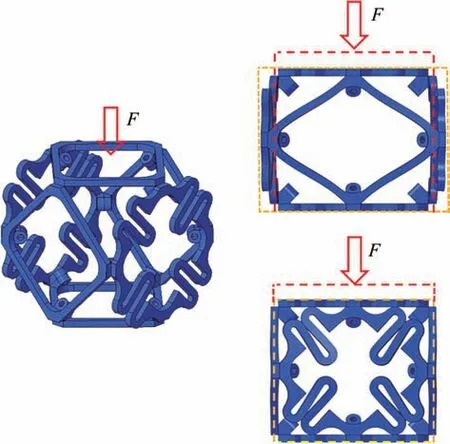
图12 混合胞元变形示意图Fig.12 Deformation diagram of mixed cell
忽略正泊松比单元的细微形变及部分连接零件的尺寸,仅考虑胞元中点位置的位移变化,可将后缘结构运动过程简化为如图13所示的结构模型,其中H为始端胞元中点与导向定滑轮间的距离,h为末端胞元中点与驱动绳末端连接处的距离。此时在xoy坐标系内柔性后缘末端的坐标为(xL,yL),末端的转角为βL,由几何关系可知驱动绳末端连接处的坐标(x,y)为

对于任意一点S的坐标为(x(s),y(s)),S点的转角为β(s),根据图13可以给出点S处的弯矩表达式为

图13 柔性后缘简化模型Fig.13 Simplified model of flexible trailing edge

此时柔性后缘结构满足如下梁曲率和弯矩的边界条件,其中EI为沿着后缘弦向的抗弯刚度。

2.3 柔性后缘结构仿真
为验证柔性后缘结构的可靠性,本文对由5 个复合胞元构成的柔性后缘进行仿真,结构材料选用PA12,对柔性后缘根部施加固定约束,为模拟单索传动机构的运动方式,将整个运动过程分解为多个载荷步骤,并对每个载荷步骤施加改变方向与大小的力载荷条件。仿真结果显示,柔性后缘结构偏转17°时整体结构的最大应力为27.27MPa,出现在襟翼根部胞元的内凹结构上,没有超过材料的许用应力,满足强度要求。从仿真结果的侧视图来看,零泊松比单元在保证后缘弯曲过程中结构并未产生横向变形,符合设计预期与目标,由于实际后缘模型还存在其他结构,因此实际的后缘偏转角θ约为22°,如图14所示。

图14 柔性后缘仿真验证Fig.14 Simulation verification of flexible trailing edge
3 变后缘机翼实物试验
为了验证变后缘机翼的变形能力,根据设计方案制作了实物机翼样段,机翼弦长约为0.8m,其中力学超材料单元采用PA12 高性能尼龙增材制造完成,蒙皮支撑部件采用光固化树脂制备,蒙皮选用硅胶制备,机翼样件中的主体零件是采用M1.6的螺栓穿过二维单元上连接孔进行固定的,蒙皮采用胶结方式粘连在后缘连接部件之上,如图15(a)所示。为保证后缘弯曲时下翼面不产生褶皱,在安装时施加部分预紧力,组装完成后的机翼样段重量为433.3g。机翼前缘通过螺栓固定在试验平台上,机翼后缘变形采用舵机进行驱动,舵机型号为DS3218,将约为0.4m 长的凯芙拉绳分别连接舵机上的舵盘与柔性后缘结构,在开发板的控制下舵盘旋转将绳收紧,带动柔性后缘产生变形。本文采用动态捕捉系统实现后缘位置捕捉,为测量变弯度机翼的变形范围,控制数字舵机多次旋转并记录后缘变形结果,后缘偏转角θ=22.4°时的变形结果如图15(b)所示,通过调控舵机可实现在1s 内柔性后缘结构到达该位置,舵机复位时,柔性后缘能够依靠自身结构在1.5s 内恢复到初始位置。图16 为绳索传动机构的绳索收缩位移△s与后缘偏转角θ之间的关系曲线,通过计算本次试验中绳索的传动比约为1.36(°)/mm,随着绳索收缩,后缘偏转角逐渐增大,绳索收缩16.5mm时偏转角约为22.4°。

图15 变后缘机翼实物试验Fig.15 Physical experiment of variable trailing edge wing
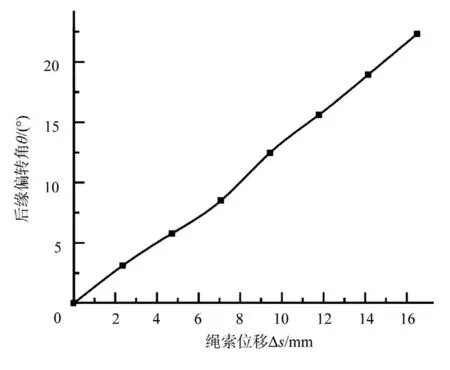
图16 后缘偏转角与绳索位移的关系曲线Fig.16 Relationship curve between trailing edge deflection angle and rope displacement
(1)由试验结果可以看出,本文设计的机翼结构能够有效实现机翼后缘的柔性变弯度,偏转角θ可达22.4°,与前述仿真结果基本一致。柔性后缘结构响应速度快,能够在1s内完成变形,快于以形状记忆合金设计的变后缘机翼,同时机翼样段整体重量(质量)轻于传统机械结构变后缘机翼。
(2)柔性后缘结构变形后的复位主要依靠蒙皮的预紧力与零泊松比单元弹性形变下的恢复能力,由于单元结构采用PA12 高性能尼龙,其具有良好的柔韧性和耐磨蚀性,能够满足这一要求,同时通过设计特定的单元结构,未来可实现可变厚度机翼等。
(3)从变形过程来看,偏转角和绳索位移之间体现出较好的线性关系,可以通过绳索收缩位移来有效控制柔性后缘结构变形。
目前,柔性后缘结构仍存在一些不足,由于在制造过程中存在热应力等问题,实际的二维单元会存在部分翘曲变形,因此胞元连接时会产生应力,将导致后缘结构向垂直于试验平台方向发生弯曲,通过改进制造工艺、合理设计驱动位置及蒙皮预紧力可解决这一问题。
4 结论
本文提出了一种基于力学超材料的柔性后缘设计方法,通过仿真研究了部分结构参数对超材料单元性能的影响,并组合了两种力学超材料单元实现三维超材料胞元的设计,在机翼气动外形优化结果的基础上完成机翼驱动、结构的整体分布设计,并通过仿真验证后缘结构变形的可靠性,通过增材制造技术完成机翼实物的制造、装配及试验,得出以下结论:(1)本文方法设计的机翼样段结构重量较轻,主体部分可由模块化的胞元快速装配,可通过连接结构进行替换、扩展,便于维修。(2)柔性后缘变形响应速度快,最大偏转角可达22.4°。(3)偏转角和绳索位移之间体现出较好的线性关系,便于控制。
受限于文章篇幅等,本文并未对柔性后缘结构承载能力作进一步测试及阐述,未来的研究中将验证其结构稳定性并扩展机翼功能。

