变弯度柔性机翼与多段翼型气动特性对比研究

李嘉仪，黄再兴，张宪政，童明波，陈吉昌

1.南京航空航天大学飞行器先进设计技术国防重点学科实验室，江苏 南京 210016

2.江西洪都航空工业集团有限责任公司，江西 南昌 330096

随着各类型飞行器的更新换代，飞机在不同飞行环境下的性能要求逐年提升。尤其是起飞着陆过程中的气动性能，在极大程度上影响飞行器的环境适用性。机翼变弯度技术使得飞机能在不同飞行状态下获得更高的飞行效率，已逐渐成为近年来的研究热点。

后缘机械增升装置通过简单机械变形以增加机翼的最大升力系数，在诸多类别的增升装置中，单缝襟翼的设计和使用相比于开裂襟翼和简单襟翼，能更大程度上优化升力特性[1]。近年来，柔性可变弯度机翼的出现，将传统变形机翼的设计观念从局部固定机构的改变，提高到了内部机构变形与智能材料外皮相结合的设计趋势上去。随着后缘增升装置的更新换代，传统后缘襟翼的优化及柔性变形机翼的使用使得机翼变体技术成为提高飞机升阻特性的一大捷径。相比于传统主翼，简单襟翼翼型，带柔性蒙皮的变弯度机翼具有更加灵活的传动结构，外形上也更光滑连续。

自20世纪90年代起，国外已开始进行柔性可变弯度机翼领域的研究，美国与欧洲各国纷纷将变弯度机翼列为关键技术。机翼后缘连续变弯度技术最早于1994年被提出，2003 年Kerr-Jia 和Kota[2]提出了一种系统化的建模方法，通过目标函数捕捉形状差异，并使用遗传算法生成了可自适应形状变化的后缘变形机构。Yokozeki和Sugiura[3]采用瓦楞结构实现了机翼后缘光滑偏转，并通过风洞试验对比了后缘连续变弯度翼型与传统单铰链副翼翼型的气动特性。Lyu 和Martins[4]基于梯度优化算法，进行了NASACRM 构型机翼变后缘弯度的气动性能分析。Kaul 和Nguyen[5]使用S-A 湍流模型，对比分析了5 种不同后缘弯度机翼与初始无偏转机翼的气动特性。国内陈钱等[6]研究了6 种外形变弯度机翼的绕流分布，分析了不同外形下连续光滑变形机翼与传统偏转翼型的气动特性，并研究了其不同气动特性的流动机理。梁海朝等[7]研究了巡航状态下连续光滑偏转后缘变弯度翼型的气动特性，得到了跨声速巡航状态下，偏转方式敏感度小于低速飞行大偏角情况的结论。杨文超等[8]搭建了风洞测力及流场显示试验平台，研究了机翼弯度连续准定常变形下的流动分离特性，并分析了变弯度机翼与固定弯度机翼流动分离现象的区别。伏欣[9]使用FLUENT对具有柔性弯曲悬臂梁后缘的变形机翼进行了气动分析，验证了其性能相比于传统机翼的优势。近年来，虽在柔性变形机翼与传统变形襟翼领域产生了诸多气动特性分析的研究成果，但对于相同飞行条件下，光滑变弯度翼型与传统多段翼型在相同后缘偏转角情况下气动特性仿真的对比研究还较少。

本文基于计算流体力学基本理论，求解二维不可压Navier-Stokes（N-S）方程，对比在相同飞行速度、雷诺数的情况下，柔性连续二维机翼与带有单襟翼的二段翼型的气动性能差异，分析并讨论在相同后缘偏转角的情况下，翼缝对二维机翼表面气流流动特性的影响，为变弯度机翼的优化设计提供参考依据。

1 研究方法

1.1 变弯度翼型建模及计算模型

在标准NACA4418 翼型基础上，本文参考相关研究进行了柔性变后缘弯度翼型[10]及单襟翼二段翼翼型[11-12]的建模，变形前弦长c均为1m。默认前缘处为坐标原点，柔性机翼转轴位置L为后缘30%弦长处。二段翼襟翼长度为30%弦长，转轴位置L为后缘25%弦长处，为保证襟翼正常偏转，单襟翼后退位移m为（10%c，0）。考虑实机飞行情况下后缘偏转角度限制，计算模型偏转角度选择满足基本飞行需求的3°、6°、9°、12°。在保证基本构型一致的前提下，调整特征尺寸以确保计算雷诺数相同。

以转轴中心与后缘点连线为初始位置，不同后缘偏转角下两种翼型与初始翼型对比如图1所示。

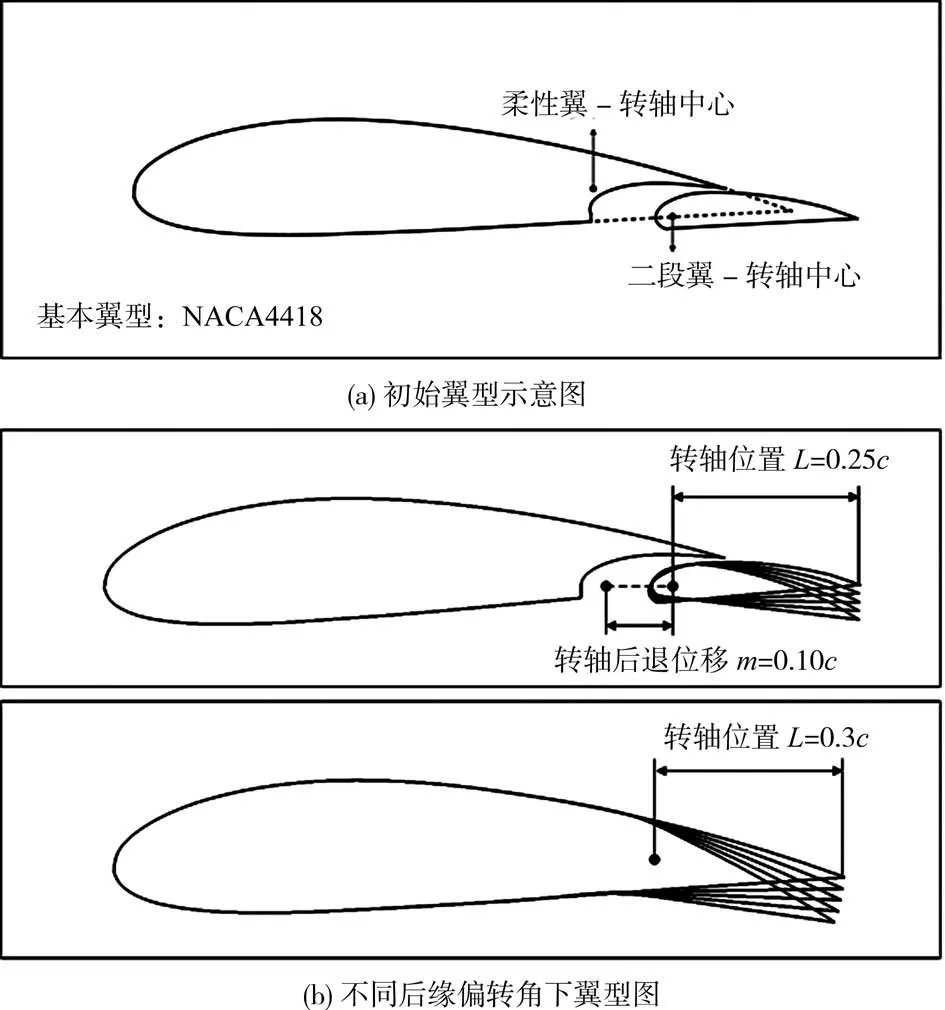
图1 翼型示意图Fig.1 Schematic diagram of airfoils

本文采用计算流体力学的方法对两种翼型进行相同参数下的气动仿真，其中涉及的雷诺平均Navier-Stokes 方程为

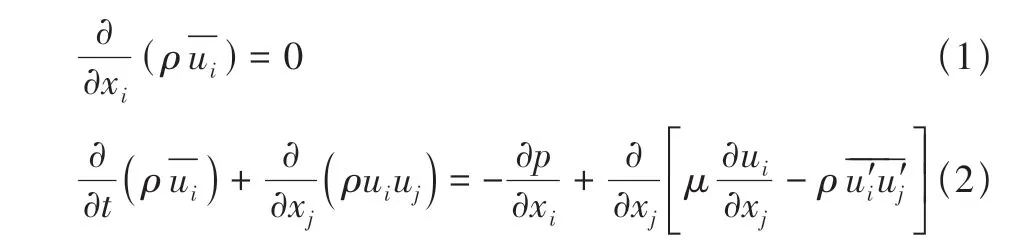
湍流模型选择一方程模型，非守恒形式的Spalart-Allmaras（S-A）模型控制方程[13]为

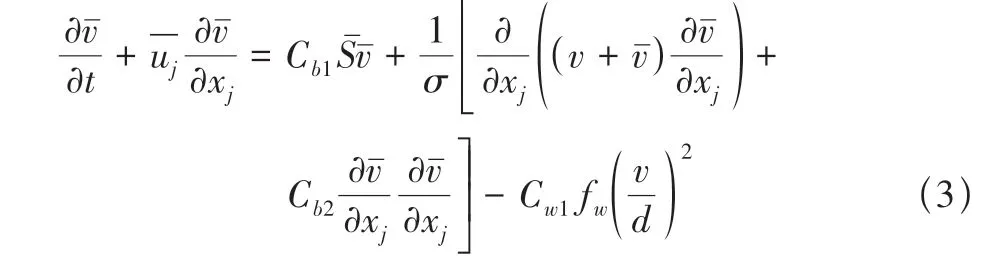
其中涡黏系数定义为

1.2 方法适用性验证

在进行主要计算之前，对GA（W）-1 翼型进行气动分析并与试验结果[14]对比，验证方法可行性。具体计算参数为v=51m/s，Re=6.3×106。计算得到不同迎角下的升力系数及力矩系数与试验结果对比如图2 所示，计算升力系数与试验数据吻合良好。

图2 算例验证结果图Fig.2 Verification results of calculation examples

为确保计算过程中网格数量不影响计算精度，基于初始柔性翼型基本工况进行网格无关性验证。在使用切割体网格的基础上，对机翼周围网格进行加密，得到6种不同网格量的计算结果（见表1）。以升力系数为例，随着网格量的增加，计算误差为0.33%～1.9%，故计算结果存在网格无关性。为节约计算资源，选用第三套网格进行计算。二段翼模型使用的网格相比于柔性翼网格，在翼缝附近进行了额外加密，网格数量增加了50%，不再进行无关性验证。整体网格情况（以二段翼网格为例）与两种翼型网格细节图如图3 所示，考虑到计算量问题，采用壁面函数法进行近壁面处流动计算[15]，取y+=30，第一层网格厚度为1.8e-4倍弦长。

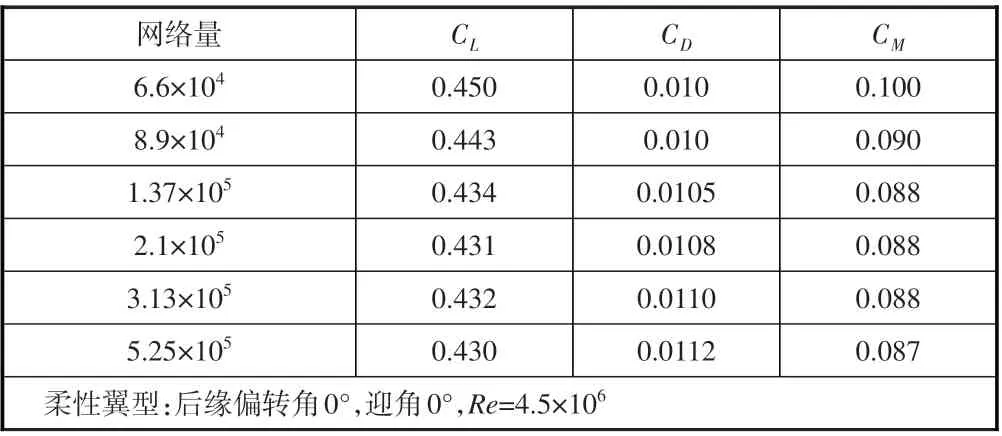
表1 不同网格数量气动力系数对比Table 1 Comparison of aerodynamic coefficients of different grid numbers

图3 整体网格及细节网格图Fig.3 Overall grid and detail grid

基于后缘偏转角6°的二段翼型进行湍流无关性验证，使用不同湍流模型进行计算，v=68m/s，Re=4.5×106。

湍流无关性验证结果见表2，不同湍流模型计算结果误差在4.3%以内，选择标准S-A湍流模型进行后续计算。

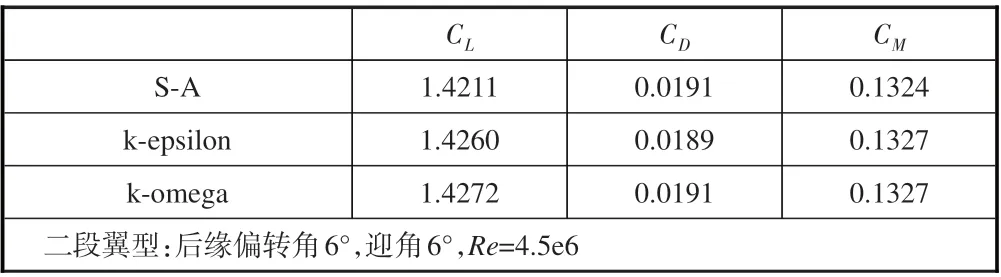
表2 不同湍流模型气动力系数对比Table 2 Comparison of aerodynamic coefficients use different turbulence models

2 研究结果

多段翼型缝道的存在会消除后缘处的主要分离，加之缝道内复杂流动现象，导致两种翼型的气动力特性随特定飞行参数变化规律而不同。考虑飞机起飞着陆过程中的飞行姿态变化，本文先针对固定后缘偏转角为0°、3°及6°，固定飞行速度v=68m/s，变迎角时两种翼型做气动仿真。继而对固定迎角，改变后缘偏转角时两种翼型的气动特性做结果分析。分别就迎角、后缘偏转角及翼缝的存在对两种翼型气动特性的影响做具体讨论。

2.1 后缘偏转角对升阻力特性的影响

2.1.1 后缘偏转角0°，迎角由-2°到16°变化

计算得到两种翼型气动数据对比如图4 所示（其中flex表示柔性，flap表示二段翼）。二者升阻力系数变化规律一致，在计算迎角小于8°时，二段翼升力系数略小于柔性翼，迎角继续增大到10°后，二段翼升力系数超过柔性翼。阻力系数上，二段翼的阻力系数始终小于柔性翼，直到达到16°迎角，即临界迎角附近时，阻力系数才近似相等。

图4 后缘偏转角为0°时，力系数及力矩系数随迎角变化情况Fig.4 Edge deflection angle 0°，variation of force coefficient and moment coefficient with angle of attack

值得注意的是，由于翼缝的存在，二段翼的力矩系数在计算迎角由-2°到16°增加的过程中，呈现先减小后增加再减小的变化趋势，与柔性翼的单调递减不同。

2.1.2 后缘偏转角6°，迎角由-2°到16°变化

图5 为后缘偏转角均为6°时，两种翼型的气动力系数变化图。两种翼型升阻力系数变化规律一致，在计算迎角小于4°时，后缘偏转6°的二段翼升力系数略小于柔性翼。随着迎角的增大，二段翼升力系数超过柔性翼。达到临界迎角之前，二段翼的阻力系数始终小于柔性翼，且随着迎角的增大，差异逐渐明显。迎角大于12°后，柔性翼翼周流动分离现象显著增加，升力系数大幅减小，阻力系数大幅增加，机翼失稳，在此过程中二段翼升阻力系数值始终规律性变化，直到迎角变化至18°时，升阻比才开始减小，但翼周流动始终处于定常状态。

图5 后缘偏转角为6°时，力系数及力矩系数随迎角变化情况Fig.5 Edge deflection angle 6°，variation of force coefficient and moment coefficient with angle of attack

同样，由于翼缝的存在，二段翼的力矩系数在计算迎角增加的过程中，呈先减小后增加再减小的变化趋势，与柔性翼的单调递减不同。

2.1.3 后缘偏转角12°，迎角由-2°到16°变化

图6为后缘偏转角均为12°时，两种翼型的气动力系数变化图。两种翼型阻力系数变化规律与后缘偏转角为0°与6°时基本相同。二段翼升力系数在迎角为0°时已然略高于柔性翼，柔性翼翼周流动在迎角增大至6°后开始发生大规模流动分离，而二段翼始终计算稳定，直到迎角增大至18°，升阻比才开始减小，翼周流动仍处于定常状态。

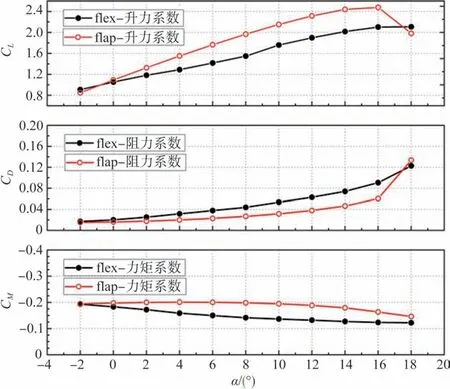
图6 后缘偏转角为12°时，力系数及力矩系数随迎角变化情况Fig.6 Edge deflection angle 12°，variation of force coefficient and moment coefficient with angle of attack

综上所述，两种翼型在升阻力系数上变化趋势基本一致，但随着后缘偏转角的增大，对柔性翼转轴附近的外形要求逐渐增高，二段翼的力矩系数变化规律则逐渐弱化，向单调递减靠拢，在后缘偏转角相同情况下，二段翼的气动特性更加稳定。

2.2 迎角固定时后缘偏转角变化对升阻力特性的影响

计算迎角固定为0°时，随着后缘偏转角逐渐增大，两种翼型升阻力系数及压力系数均呈单调递增的变化规律，其中柔性翼升力系数始终略大于二段翼，阻力系数在后缘偏转角增大至9°之前也始终小于二段翼。力矩系数反之，二段翼力矩系数在后缘偏转角增大至9°之前始终小于柔性翼，如图7所示。

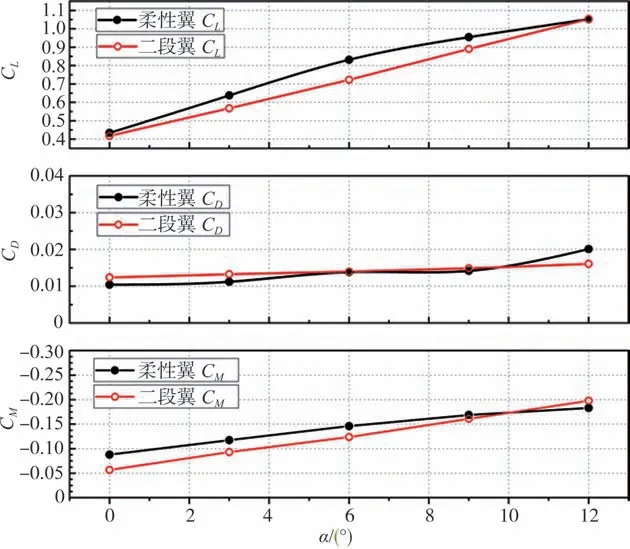
图7 迎角为0°时，力系数及力矩系数随后缘偏转角变化情况Fig.7 Variation of force and moment coefficients with 0°angle of attack at subsequent edge deflection angles

计算迎角固定为6°时，二种翼型升阻力系数及压力系数均呈单调递增的变化规律，二段翼升力系数在后缘偏转角小于6°时略小于柔性翼，偏转角大于6°后二段翼升力系数稳定增加，差距在9°后逐渐明显，如图8 所示。

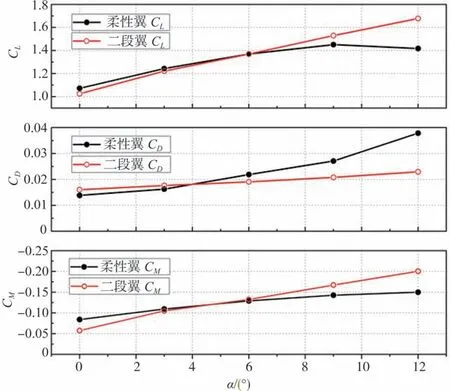
图8 迎角为6°时，力系数及力矩系数随后缘偏转角变化情况Fig.8 Variation of force and moment coefficients with 6°angle of attack at subsequent edge deflection angles

计算迎角固定为12°时，二种翼型升阻力系数及压力系数均呈单调递增的变化规律，二段翼升力系数始终高于柔性翼且增长幅度更大，二段翼阻力系数也更低，整体升阻比在各种偏转角下都优于柔性机翼，如图9所示。

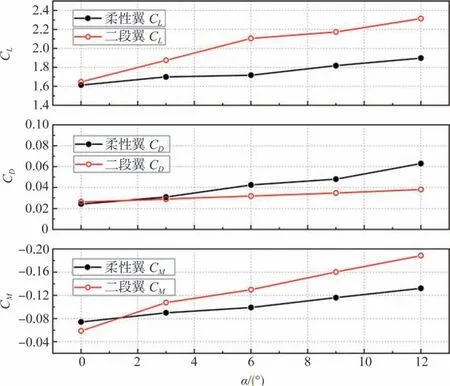
图9 迎角为12°时，力系数及力矩系数随后缘偏转角变化情况Fig.9 Variation of force and moment coefficients with 12°angle of attack at subsequent edge deflection angles

随着迎角的增大，两种翼型改变后缘偏转角带来的增升减阻效果差异也逐渐明显，整体上看，二段翼的气动性能提升得更快，且更加稳定。

2.3 后缘偏转角对翼型表面压力系数及翼周速度的影响

二段翼翼缝的存在使得翼型表面流动情况在翼缝周围与连续翼型有较大的区别，气流流过时将在翼缝内短暂停留后分别沿襟翼上下表面向后移动，并在后缘点汇聚成一股。图10所示为固定迎角为6°时不同后缘偏转角下两种翼型表面的压力系数分布情况。随着后缘偏转角的增大，两种翼型前缘上表面压力系数差距逐渐增大，这一点从云图中也可看出，6°后缘偏转角、12°迎角时两种翼型前缘驻点位置基本相同，但翼型上表面已有明显速度差异，此时柔性翼前缘上表面最大速度为122m/s，而二段翼前缘处则达到了135m/s。

图10 不同后缘偏转角翼型表面压力系数分布情况Fig.10 Surface pressure coefficient distribution of airfoils with different trailing edge deflection angles

结合图10与图11可知，两种翼型翼周速度在后缘处差异同样明显，随着后缘偏转角的增大，柔性翼上表面偏转轴附近的流动分离现象逐渐加剧，尾迹湍流区相比于二段翼更宽，此时流场已为非定常，流动不稳定直接导致了柔性翼升阻比的下降。

图11 迎角为6°时不同后缘偏转角的速度云图Fig.11 Contours of velocity with different trailing adge deflection angles at 6°angle of attack

二段翼翼缝处流动湍乱产生小涡，从图10 中也可看出，翼缝附近压力系数浮动明显，且随着偏转角的增大，流过翼缝的气流逐渐规律化，襟翼翼周压差趋于稳定，襟翼表面压力系数分布情况与普通单个翼型接近。

综上所述，在后缘偏转角较小时，柔性翼的气动特性优于单襟翼翼型，随着偏转角的增大，柔性翼后缘转轴处的结构设计将直接决定其在增升上的优势，转轴处衔接面弧度影响着柔性翼翼型尾迹大小，而单襟翼翼型翼缝的存在虽在一定程度上影响了机翼表面流动，但在大后缘偏转角的情况下，气动特性表现更好。

3 结论

本文通过求解二维不可压N-S 方程，研究了在亚声速飞行中，不同迎角及不同后缘偏转角情况下二维柔性机翼翼型及二段翼翼型的气动特性，可以得到以下结论：

（1）柔性翼与二段翼的升阻力特性在后缘偏转角度小时，变化趋势基本相同，随着后缘偏转角度的增大，二段翼升力系数曲线在更小的迎角下反超柔性机翼，阻力系数变化趋势也缓慢于柔性翼。

（2）柔性翼与二段翼的升阻力特性在飞行迎角小时，随着后缘偏转角的改变，其趋势基本相同。二段翼升阻力系数均稳定增加，而柔性翼在迎角增大后，随着后缘偏转角的增大，更容易产生大规模流动分离。

（3）柔性翼在不同迎角下后缘附近的流动分离发生在后缘转轴附近，随着后缘偏转角和迎角的增大，流动分离现象逐渐明显。二段翼翼缝内部涡流的产生导致整体压力系数在翼缝附近浮动，此为两种翼型升阻比存在差异的主要原因。

（4）后缘偏转角小时，柔性翼气动特性优于单襟翼翼型，后缘偏转角大时则反之，此现象取决于柔性翼后缘转轴处结构外形及单襟翼翼型翼缝形状。