基于改进Hybrid A*的旋翼无人机路径规划算法

彭锦城，彭侠夫，张霄力，陈锦文

厦门大学，福建 厦门 361102

近年来，四旋翼无人机由于具有机动性强、灵活方便、应变能力强、价格便宜等特点，逐渐成为识别、检测、监控、侦察等任务的理想飞行载体[1]。目标识别是监控和侦察等后续任务的基础，具有重要的研究意义。但是，现有的路径规划算法容易造成无人机目标丢失和检测精度低等问题。

在无人机快速转动或翻转等情况下，采集的图像数据模糊，从而目标识别YOLO v3 算法会出现准确度降低、目标丢失、检测出错等问题。因此，在无人机导航飞行过程中，一条平滑、鲁棒与安全的路径，对提高四旋翼无人机的目标识别精度具有重要的研究意义[13]。

现今，无人机的路径规划算法可以分为基于优化的方法和基于搜索的方法，其中，基于优化的方法依赖于平滑和碰撞的约束函数，轨迹本身可以表示为多项式[2-3]。基于搜索的路径规划算法在栅格地图上搜索一条非光滑的路径，这条路径可以是参考文献[4]和文献[5]中提到的栅格路径，也可以是基于采样路径的快速搜索随机树法（RRT）或概率路标法（PRM）[6-7]。

然而，无论是基于搜索还是基于优化的方法所规划出的路径，都是非光滑的，降低了目标检测算法的准确率。参考文献[8]～文献[10]结合前端的路径搜索算法与后端的轨迹优化，能够生成一条符合无人机动力学和运动学的运动轨迹。但是这些算法却过于追求无人机的飞行速度，导致无人机在目标检测过程中，出现准确率不高和目标丢失等问题。

为了提高目标识别YOLO v3算法的准确度，本文采用改进二维的Hybrid A*算法，在前端生成三维的无人机飞行路径，然后在后端对生成的路径进行平滑和碰撞优化，并通过B样条优化算法生成一条平滑、鲁棒与安全的飞行轨迹。改进无人机飞行轨迹的平滑性和鲁棒性，从而提高了无人机目标识别算法的准确率，本文方法的创新性主要体现在：（1）改进自动驾驶汽车Hybrid A*二维的路径规划算法，并应用于四旋翼无人机三维的路径规划；（2）在改进Hybrid A*算法的基础上，对前端生成的路径，采集相应的控制点，使用n次导数来作为约束函数轨迹的积分项，进行平滑处理；（3）改进四旋翼无人机飞行轨迹，提高无人机快速运行时的鲁棒性，从而提高目标检测的准确率的方法，并与现有方法进行性能对比。本文提出的路径规划改进算法提高了无人机在快速飞行时的鲁棒性，从而提高无人机目标识别、检测和侦察时的准确度，对无人机侦察等应用具有重要的研究意义。

1 基于改进Hybrid A＊算法的前端路径规划

Hybrid A*算法来自自动驾驶汽车的应用，在栅格地图中搜寻到一个符合汽车运动的、安全的二维路径，搜索过程与传统的A*算法相似，创建OPEN 列表和CLOSE 列表，在OPEN 列表中找到规划代价最小的父节点，扩展父节点周围的节点，同时记录不在CLOSE列表中子节点的距离起点开销G和启发式开销H，当子节点的总开销比父节点小，更新父节点，直到找到目标点或者OPEN列表为空时，结束循环。本节在Hybrid A*的基础上，改进二维Hybrid A*算法，使其应用于三维的四旋翼无人机路径规划搜索，结合四旋翼无人机动力学和运动学，在3D的栅格地图中生成前端路径。

1.1 可行运动点的生成

无人机在运动的情况下，需要考虑运动学的因素，而传统A*算法只有节点的扩散，搜索的路径不符合无人机飞行，且在自动驾驶汽车中，离散控制输入是在二维平面的，在坐标系中，控制二维平面只有xy轴，而无人机的控制是在三维平面的，需要考虑z轴的控制。因此，首先将无人机的运动分解为三个二维平面[8]，再分别进行处理，得到下一次无人机的运动点

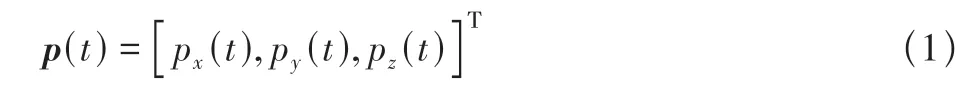
式中，px(t),py(t),pz(t)分别表示为x，y，z三个平面上的点。

无人机的状态方程可以表示为s=[x,y,z,ẋ,ẏ,ż]Τ，系统的输入为u=[ẍ,ÿ,z̈]Τ，系统模型表示为ṡ=A∗s+B∗u。

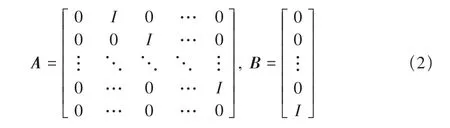
状态转移方程为

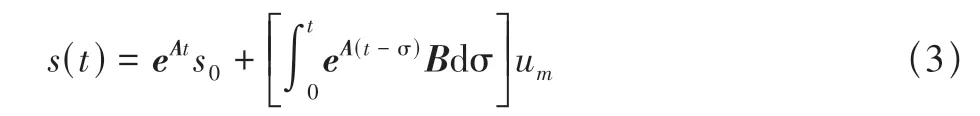
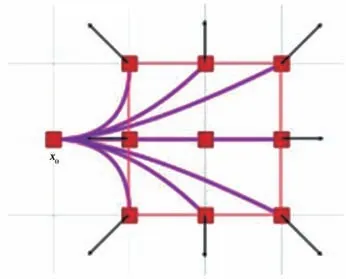
图1 离散控制输入得到下一刻无人机的可行运动点Fig.1 The discrete control input is used to obtain the feasible movement point of the UAV at the next moment

1.2 构建最优边值问题计算启发式开销

在传统的A*算法中，直接使用欧式距离，且只考虑栅格地图中障碍物的信息，而忽略了无人机的运动学和动力学特性，本文所采用的方法是通过计算最优边值问题，来计算启发式的开销。启发式开销模型可表示为

式中，u(t)为控制输入。构建最优边值问题模型

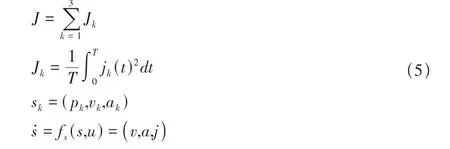
式中，Jk为所求的开销；sk为无人机状态；jk为无人机的控制输入；ṡ为系统方程。根据庞特里亚金极小值原理，引入协态λ，建立哈密顿方程为

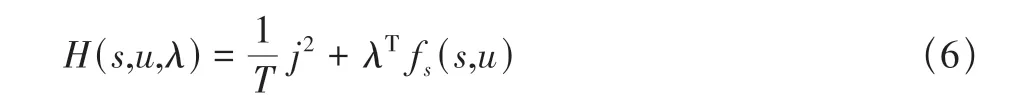
可求得最优的控制输入为

三阶多项式轨迹方程为

式中，pμc,vμc是无人机当前位置和速度；αμ,βμ为未知变量，其解析式为

式中，x1=pμg-pμc-vμcT，x2=vμg-vμc，pμg,vμg为无人机目标位置和速度，根据所求的最优控制输入u∗(t)，代入式（10）

求得启发式开销为

1.3 节点的扩展及剪枝

在可行运动点生成的基础上，比较不同节点的开销f=g+h，其中g为实际开销，h为启发式开销，选择开销最小的节点进行扩展，并把开销大的路径剪枝，在满足动力学和运动学的基础上，完成路径的搜索。在离散控制的情况下，目标原点的状态很难准确达到，因此，如果满足安全性和动态可行性要求，且在目标点一定范围内，则可以提前终止搜寻，以提高搜寻的效率。节点的扩展如图2所示。

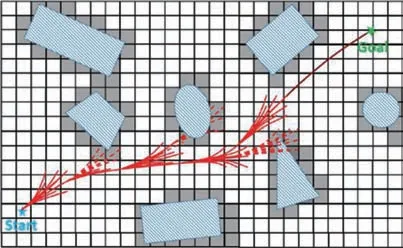
图2 节点扩展搜寻图Fig.2 Node expansion search diagram

2 基于B样条算法的后端轨迹优化

在栅格障碍物地图中，前端生成的改进Hybrid A*路径往往会很靠近障碍物，这样对无人机的运动飞行是不合理的，因此需要对前端生成的路径进行优化，利用ESDF地图提供的距离信息和梯度信息，进行优化，生成平滑、鲁棒、安全的飞行轨迹。

2.1 控制点的求解

对前端生成的次优路径进行等时间T采样，得到K段路径以及每段轨迹的首末位置pk、速度vk和加速度ak，每段轨迹利用最小二乘近似求解超定方程，得到控制点

式中，ps,pe为首尾端点位置；vs,ve为首尾端点速度；p0,p1,p2,p3为控制点位置。

2.2 控制点的优化

对次优路径的采样取点，求得的控制点也是次优的，需要对它进行非线性优化处理，从而得到平滑、鲁棒、安全的轨迹，总约束函数模型的建立如下

式中，fs,fc是路径平滑度和碰撞安全性的代价函数；fv,fa是速度和加速度的代价函数，限制着无人机的速度和加速度，提高无人机的鲁棒性和安全性；λ1,λ2,λ3为三者的权重。

平滑代价函数fs：在文中，平滑函数可以表述为使用i次导数代价来作为代价函数轨迹的积分项（加速度、加加速度等）[12]，其定义如下

碰撞代价函数fc：轨迹点在距离障碍物的τ范围内，函数表示如下

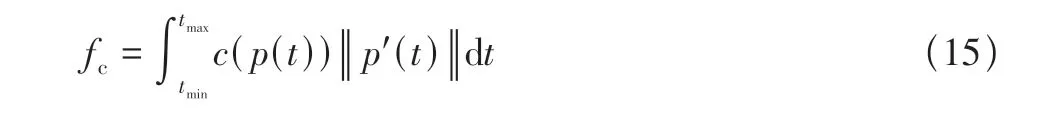
其中，每个点的c(x)代价函数定义如下

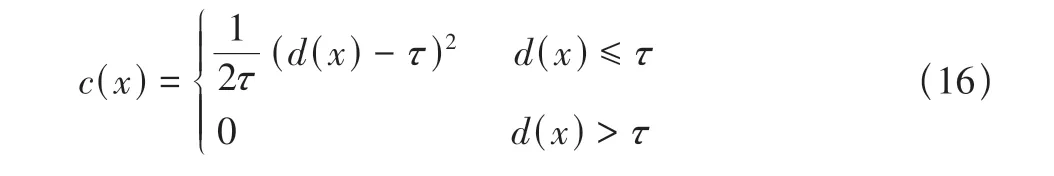
d(x)表示与障碍物最近的距离。速度和加速度的代价函数fv,fa，将不可行速度和加速度控制点进行约束

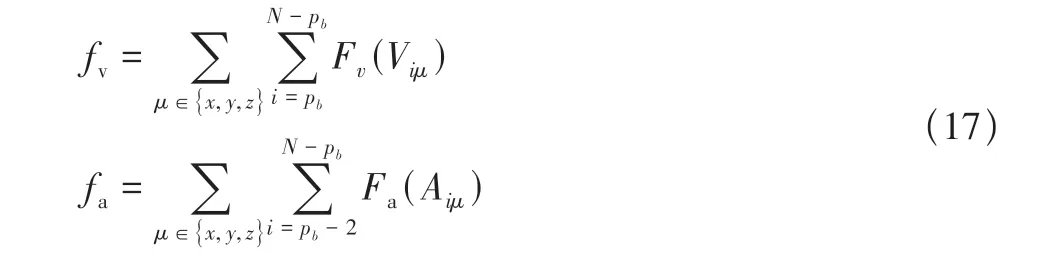
其中，μ∈{x,y,z}，最大允许速度为vmax，且Fv(vμ)定义如下

2.3 B样条轨迹的生成

本文轨迹优化的方式采用B 样条方法[11]，在生成控制点以及对控制点进行优化处理后，得到平滑的轨迹。K-1次B样条的公式计算为

式中，S(t)表示优化后的轨迹；Ni,k(t)是基函数表中第i个k次B 样条的基函数；Qi为第i个控制点。基函数是使用Deboor算法生成的，表达式如下

式中，ui表示节点，Ni,k(u)表示基本函数表中的基函数。

3 试验结果与分析

3.1 试验设置与试验平台

使用DP1000四旋翼无人机多次进行户外测试来试验。所提出的相关路径规划和轨迹优化方法，均在TX2板载计算机、Ubuntu18.04 系统、ROS 平台上使用C++代码试验。调用非线性优化求解器NLopt 对控制点进行优化处理，在真实无人机上验证算法之前，已在gazebo 进行了若干次试验，确保算法可行的情况下，才进行真实无人机试验。

在未知的环境中，使用DP1000 四旋翼无人机平台，进行目标识别和无人机自主避障飞行，如图3所示，PX4飞控板，配备英特尔实感深度摄像头D455，生成密集点云图，用于栅格障碍物地图的绘制，本文使用扩展卡尔曼滤波（EKF）将GPS 和IMU 的数据进行融合，从而获得位姿信息。路径生成、轨迹优化、状态估计和ESDF地图构建均在Nvidia TX2（配备8GB RAM、8GB SSD 和256GB 外部存储器）板载计算机上进行，通过ROS节点，将图像信息以话题/camera/color/image_raw 的形式，传输到地面端Lenovo Legion Y7000P 笔记本电脑进行目标识别、检测和侦察。DP1000无人机如图3所示。

图3 无人机平台Fig.3 UAV platform

3.2 试验结果分析与比较

对于本文提出的改进Hybrid A*算法结合后端优化的方法，主要进行两个方面的测试：（1）不同算法路径的比较，测试参数为：路径的平滑程度和飞行过程中的最大加速度和平均加速度。（2）无人机在快速飞行过程中，对比不同算法的目标识别的准确率和检测数目。随机放置2.5m和3.0m的避障杆，让无人机自主穿梭，并进行目标识别和侦察。在快速飞行时，四旋翼无人机能够成功地生成平滑、鲁棒、安全的路径避开障碍物，且提高了目标识别和检测的准确率。

3.3 无人机运动的路径比较

将不同的算法生成的路径与本文提出的优化算法进行对比。无人机运行最大速度设置为0.5m/s，最大加速度设置为0.5m/s2，飞行高度为2m。对比不同算法生成轨迹的弦长和弧长的距离，来判断无人机飞行路径的平滑度，见表1。将Fast planner[8]规划的轨迹与本文算法规划的轨迹在图4中进行对比，路径的平滑度增加了10%。

表1 不同算法在无障碍物时生成的路径平滑程度Table 1 Path smoothness degree generated by different algorithms without obstacles

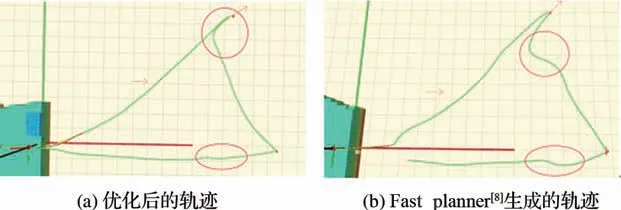
图4 轨迹对比Fig.4 Trajectory comparison

不同算法下，通过无人机快速飞行最大加速度和平均加速度来比较无人机飞行的平稳性，试验结果见表2。

表2 无人机在不同算法下飞行的鲁棒性Table 2 Robust performance of UAV flying under different algorithms

真实障碍物环境飞行如图5 所示，图5（a）表示无人机飞行的真实环境，图5（b）表示无人机局部的飞行轨迹，经本文算法优化后，绕障轨迹平滑，由图5可知，经优化后，无人机避障飞行轨迹平滑。无人机在自主导航飞行中进行目标识别，如图6所示。

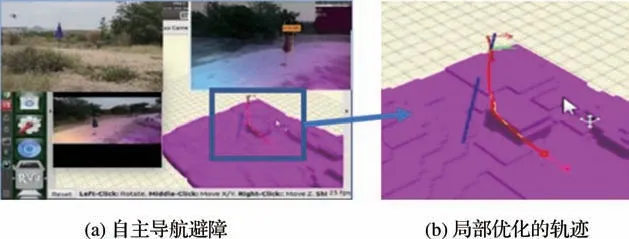
图5 真实环境中无人机自主导航Fig.5 Autonomous navigation of UAV in real environment

图6 无人机目标识别结果Fig.6 UAV target recognition results

3.4 目标识别和检测准确率

无人机高机动飞行往往导致采集的图像数据模糊，对后续的目标识别造成影响[14]。将本文改进的算法、A*算法和Fast planner 算法进行对比。无人机沿不同算法生成的轨迹快速飞行，并对特定的物体进行识别和检测，现场布置了一个人和9辆车，对比在不同算法高机动飞行下，无人机检测出的数目以及各个物体的准确率，见表3。不同算法的对比，如图7和图8所示。

图7 无人机在快速飞行时的目标识别Fig.7 Target recognition of UAV in fast flight

图8 经本文优化算法后的目标检测结果Fig.8 Target recognition diagram of UAV when the optimized algorithm flies fast

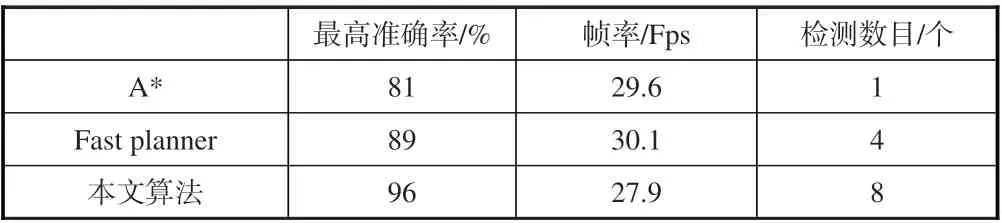
表3 不同路径规划算法对目标识别的影响Table 3 Compares the effects of different path planning on fast flight on target recognition

经过真实四旋翼无人机实际测试可知，改进的路径平滑优化算法，提高了无人机飞行的平稳性，四旋翼无人机在快速飞行中准确率不高、目标丢失等问题，得到了很好的改善。

4 结论

本文针对无人机飞行过程中的目标识别YOLO v3 算法准确率不高等问题，通过改进无人机前端路径搜索算法和后端非线性平滑优化方法，计算得到一条平滑、鲁棒与安全的飞行路径，从而提高目标识别YOLO v3算法在无人机上的准确率。改进Hybrid A*前端三维路径搜索的启发式函数和后端非线性优化的平滑函数，解决了无人机在自主导航和自主避障飞行中快速旋转或翻转等问题。本文的算法具有以下几个优点：（1）无人机快速飞行时鲁棒性和路径的平滑性得到提高；（2）无人机飞行过程中传统目标识别算法的检测精度更高。试验结果表明，本文改进Hybrid A*前端启发式函数和后端平滑优化函数，能够提高无人机飞行的稳定性和路径的平滑性，对提高目标识别的准确率有很好的效果。