柔性后缘可变形机翼气动弹性分析方法研究
赵仕伟,阚梓,李道春
北京航空航天大学,北京 100191
可变形机翼可以根据飞行环境和飞行任务的变化光滑、连续地改变自身形状,使飞机在整个任务周期内的总体性能达到最优。然而其光滑连续变形的气动外形特性导致非定常气动力变化剧烈,需采用高精度气动力分析方法。传统计算流体力学(CFD)气动分析方法[1]相比面元法[2]和降阶方法计算精度高,但计算量大、耗时多,不便于开展气动弹性分析。气动力模型降阶可建立一种精度高、适应性强的可变形机翼非定常气动力模型,用于可变形机翼气动弹性分析计算。
目前,常见的有两类降阶非定常空气动力学建模方法:流场特征分析方法和系统辨识方法。流场特征分析方法针对整个流场进行模型降阶分析,得到流场的特征状态参数;包括正交分解(POD)方法[3-6]和谐波平衡(HB)方法[7-9]。基于流体计算模型的输入响应获得正交基,模型的状态量可视为该组正交基的线性叠加,可以通过增加模型阶数从而更准确地模拟实际流场运动特性。但该方法通常用于流场的分析,由于模型考虑整个流场状态特性,模型较为复杂、阶数较高,不便于开展气动弹性分析。
系统辨识方法对流场的某些特定参数(如升力系数、力矩系数等)进行系统特征识别。非定常气动力系统辨识常见的有Volterra级数方法[10-11]、线性状态空间模型[12-13]、自回归移动平均(ARMA)模型[14]、基于人工神经网络的替代模型[15-16]、径向基函数(RBF)插值和Kriging模型[17-20]、支持向量机(SVM)方法[21-22]、状态观测器[23]、面向块的Wiener 模型[24-25]等。
采用非定常气动力降阶模型,可以提高柔性后缘可变形机翼的气动弹性响应计算效率,常见的模型降阶方法有带外输入的自回归模型(ARX)方法和Volterra 级数方法。ARX方法的非定常气动力模型阶数相比Volterra级数方法要低一个量级左右,计算效率比Volterra 级数高。因此,本文采用ARX方法建立三维非定常气动力,与结构状态空间模型相耦合,得到柔性后缘可变形机翼气动弹性系统的状态空间模型,在此基础上计算柔性后缘可变形机翼的颤振特性和阵风响应。
1 气动弹性状态空间模型
非定常气动力ARX模型可以写成如下表达式
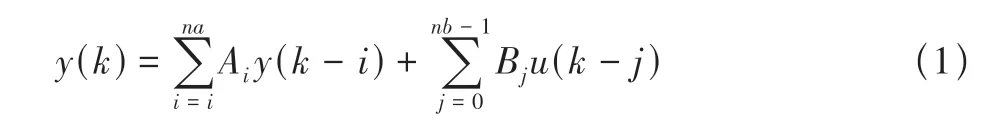
式中,y(k)表示第k步的广义气动力系数,na、nb是系统广义气动力系数输入和广义位移输入阶数,可以将该系统改写成离散状态空间的形式
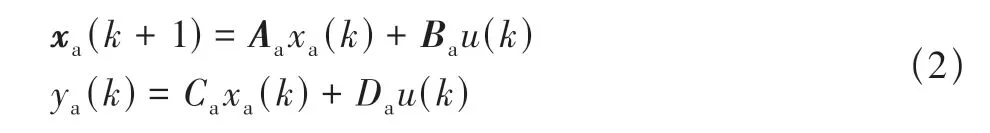
式中
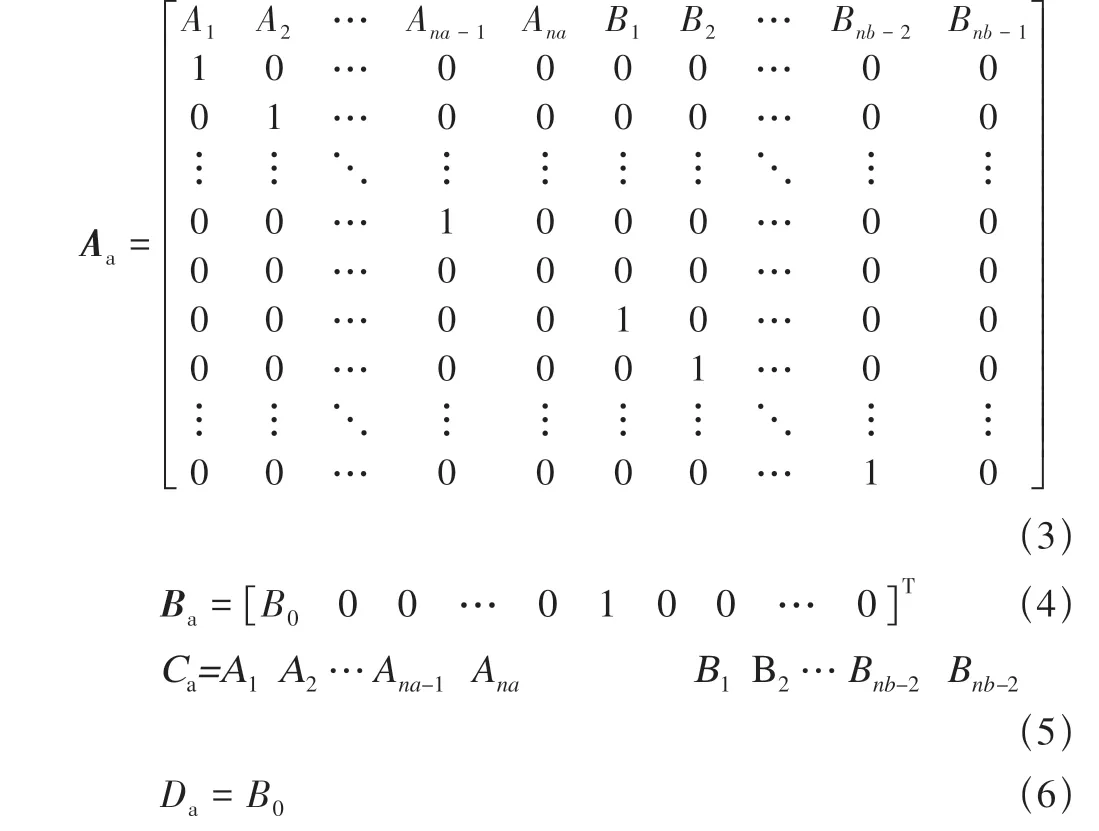
状态矢量如下
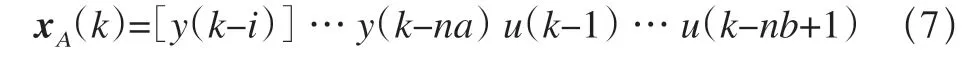
对于多自由度系统,通过归一化可以转换为模态坐标运动,结构模态坐标下的动力学方程可表示如下

其中,M为系统质量矩阵,归一化处理后是单位矩阵;C为系统阻尼矩阵;K为该多自由度结构系统刚度矩阵;x,ẋ,ẍ分别为该系统位移、速度、加速度。各阶模态对应的广义气动力FA为动压q、压力系数Cp和结构模态分析得到的各阶振型矢量Si的乘积在各个气动表面元上的积分

该系数可以Fluent 数值仿真获取。通过编写UDF 程序,在每一个时间步输出对应的各阶模态对应的广义气动力,从而得到各阶模态输入下的各阶模态对应的广义气动力。
将上述模态坐标下的动力学方程写成状态空间表达形式,可以得到
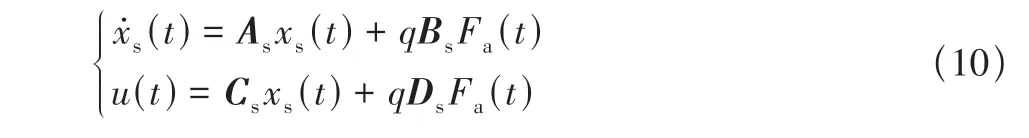
式中
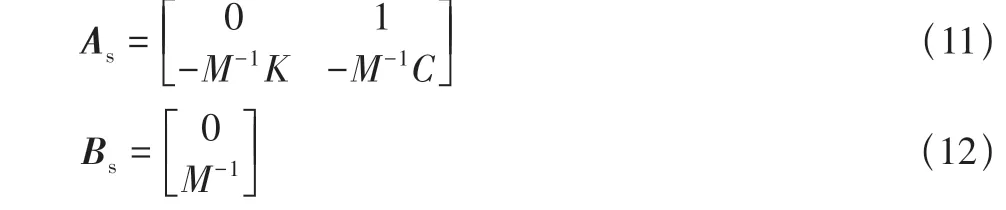

状态矢量xs(t)为

将上述连续时间系统状态空间结构模型进行离散化处理,得到对应的离散状态空间模型如下

其中:

式中,T为时间步长,上述过程为系统的结构动力学模型的获取流程,广义气动力为系统输入,结构弹性变形为系统输出。
通过ARX 方法建立离散形式的气动力状态空间模型如下

式中,u(k)为系统的广义结构位移;yA(k)为系统的广义气动力。
将基于ARX 方法建立的气动力状态空间模型和结构状态空间模型相耦合,可以得到整个气动弹性系统的状态空间模型,可以用于分析系统的气动弹性特性,计算系统的气动弹性响应。气动弹性系统状态空间模型表达式如下
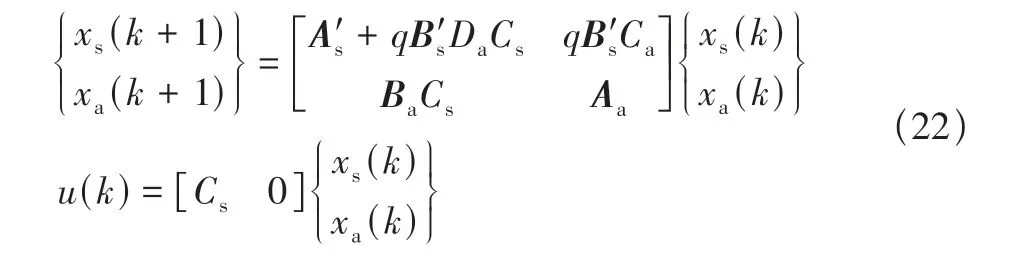
上述状态空间模型可以通过气动弹性响应计算或者矩阵特征值来分析该气动弹性系统的稳定性。通过调整速度和调整动压,从而获得对应速度下的系统响应,当响应幅值随着时间变化保持不变,该速度对应该马赫数下的颤振速度。也可以求解状态空间的特征值来分析该系统的稳定性。对于离散系统,当所有特征值模长均小于等于1时,该系统稳定;若至少有一个特征值模长大于1,该系统不稳定。可以将离散状态空间模型转化为连续状态空间模型来分析系统稳定性,当且仅当所有系统的特征值实部小于0,该系统稳定。
通过ARX 方法同样可以建立离散形式的阵风气动力状态空间模型,如下所示
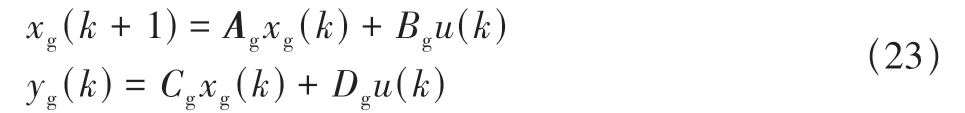
式中,xg(k)为阵风输入;u(k)是系统的广义结构位移;yg(k)是系统的阵风广义气动力。
将基于ARX 方法建立的气动弹性状态空间模型和阵风响应气动力状态空间模型相耦合,可以得到考虑阵风响应气动弹性系统的状态空间模型,用于分析系统的阵风响应。气动弹性系统状态空间表达式如下
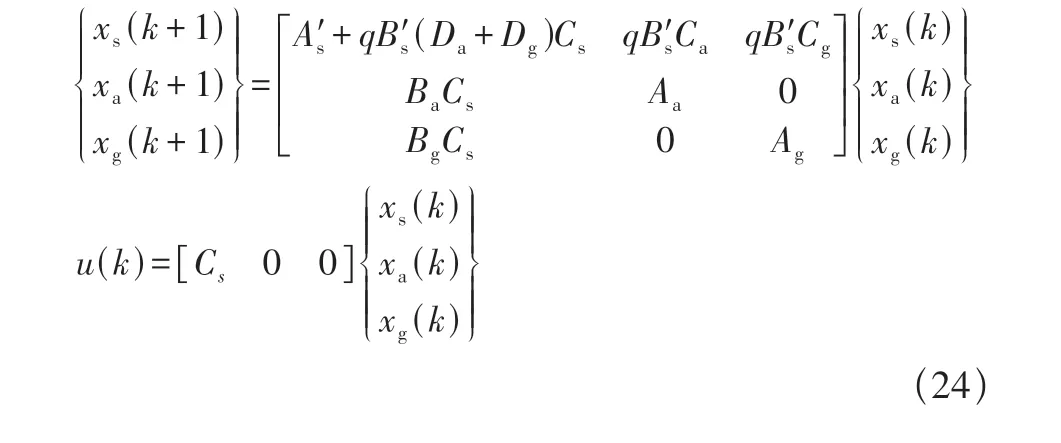
2 气动弹性特性分析方法验证
为验证基于ARX 方法建立的气动力降阶模型的有效性,本文采用Agard445.6 机翼模型。Agard445.6 几何形状如图1 所示,机翼根部弦长0.559m,半展长0.762m,展弦比为1.65,梢根比为0.66,后掠角为45°,翼型为NACA 65A004。设置结构网格最大尺寸为10mm,对机翼根部所在的平面使用固支约束,对该结构模型进行模态分析。图2为Agard445.6 机翼对应的前四阶模态振型,前四阶模态的振动频率与实验结果对比见表1,最大误差为3.15%,有限元与试验结果[26]吻合较好。
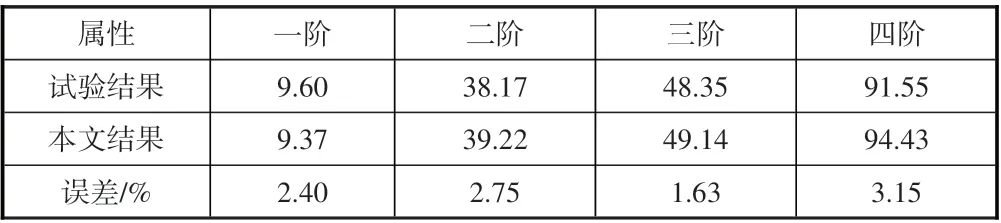
表1 前四阶模态的振动频率与试验结果对比Table 1 Comparison between the vibration frequency of the first four modes and the experimental results
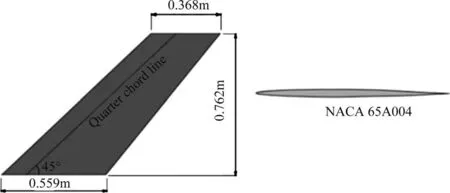
图1 Agard445.6几何形状Fig.1 Geometry of Agard445.6

图2 Agard445.6机翼前四阶模态振型图Fig.2 The first four modal shapes of Agard445.6 wing
图3 所示为Agard445.6 机翼非结构网格并导入Fluent中计算。远场边界位于距机翼20倍翼根弦长处,并设置为压力远场条件。机翼表面设置为无滑动静态壁面条件,网格在翼型附近被细化。采用动态网格结合用户自定义函数(UDF)接口编程,采用弹簧方法进行网格重构实现机翼的模态位移连续变形。在数值计算中,采用双精度求解器进行数值模拟,采用Spalart-Allmaras湍流模型。

图3 Agard445.6机翼气动网格Fig.3 Aerodynamic grid of Agard445.6 wing
图4所示为颤振马赫数和参考文献[24]的对比,可以看出,二者的数值和趋势均具有良好的一直性,最大误差小于8%。
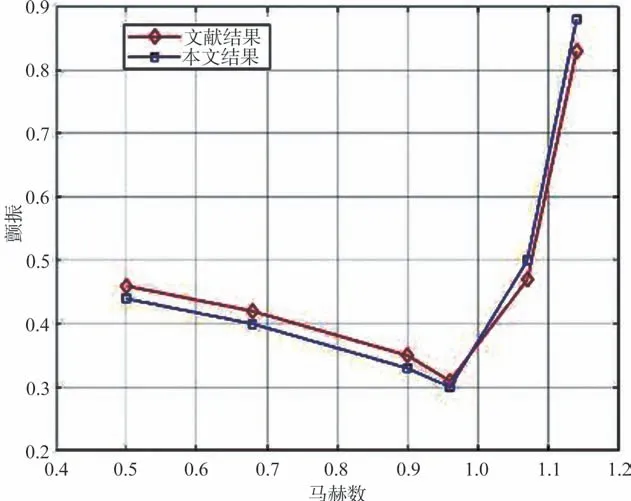
图4 颤振马赫数对比验证Fig.4 Flutter Mach number verification
图5所示为动压对应的马赫数为0.29时Agard445.6机翼各阶模态时域响应,从图5中可以看出,各阶模态位移随着时间变化位移逐渐减少呈收敛趋势,说明在该动压下该机翼尚未达到颤振。通过分析离散状态空间模型可以看出,最大特征值模长为0.994,小于1,该系统稳定。通过分析连续状态空间模型的特征值也可以看出,在该状况下所有特征值的实部均小于0,该系统稳定。图6所示为动压对应的马赫数为0.3时Agard445.6机翼各阶模态时域响应,从图6 中可以看出,各阶模态位移随着时间变化位移基本保持不变,说明动压对应的马赫数为0.3 时非常接近颤振速度。图7所示为动压对应的马赫数为0.31时Agard445.6机翼各阶模态时域响应,从图7中可以看出,各阶模态位移随着时间变化位移逐渐增大,说明该马赫数已经超过颤振速度了。通过分析离散状态空间模型可以看出,最大特征值模长为1.0003,该系统发散。通过分析连续状态空间模型的特征值也可以看出,在该状况下所有特征值存在特征值0.2917±91.8737i实部大于0,该系统发散。
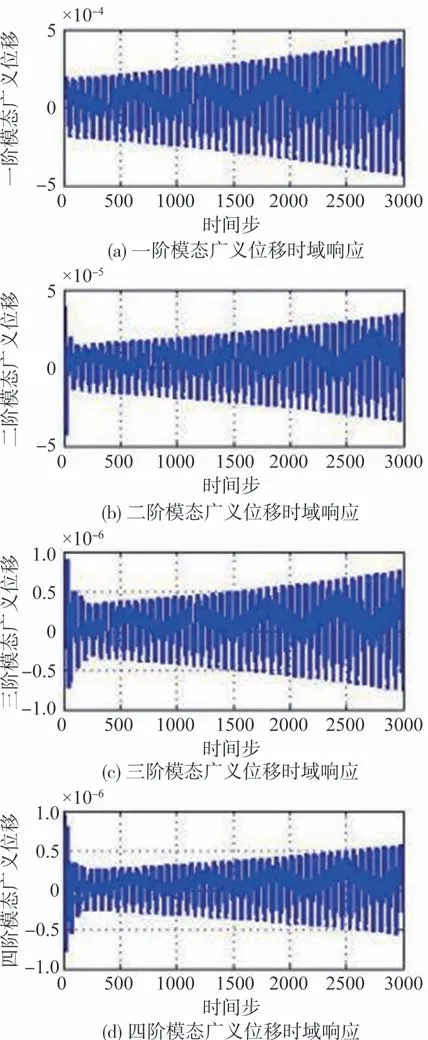
图5 Ma=0.29时Agard445.6机翼各阶模态时域响应Fig.5 Time domain response of various modes of Agard445.6 wing at Ma=0.29
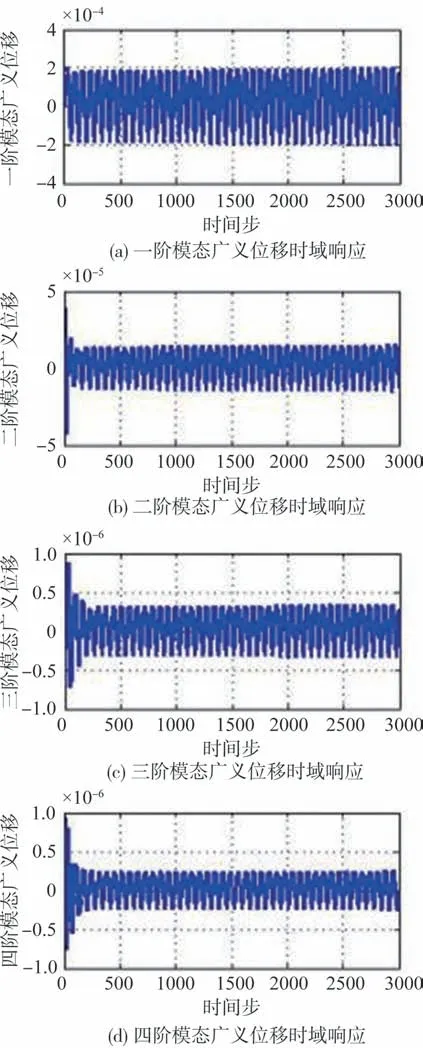
图6 Ma=0.3时Agard445.6机翼各阶模态时域响应Fig.6 Time domain response of various modes of Agard445.6 wing at Ma=0.3
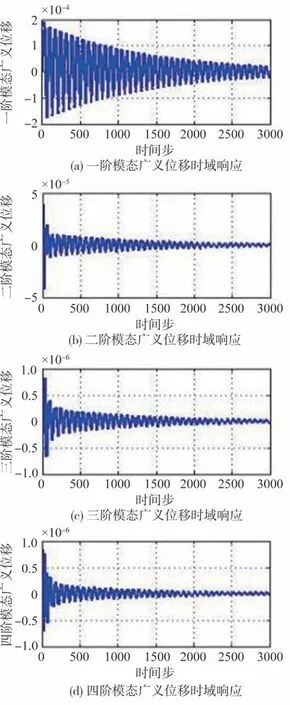
图7 Ma=0.31时Agard445.6机翼各阶模态时域响应Fig.7 Time domain response of various modes of Agard445.6 wing at Ma=0.31
3 柔性后缘可变形机翼气动弹性分析计算
3.1 颤振分析计算
本节考虑柔性后缘机翼在不同偏角下的颤振速度计算,仅考虑气动外形变化对气动弹性特性的影响,柔性后缘可变形机翼的流体网格如图8(a)所示。弦向变化范围为翼型60%到后缘部分,这一段翼型中弧线变形采用作抛物线轨迹变弯,定义60%翼型处中弧线所在的位置和变形后的后缘点的连线与初始翼型中弧线的夹角为后缘偏角β,向下偏为正偏转方向。
为节约网格绘制时间,对不同柔性后缘偏角情况采用同一套流体网格进行CFD 仿真计算。在计算某一特定偏角时,可以基于UDF程序预先将该部分后缘偏转至给定的角度,图8(b)所示为机翼柔性后缘偏转6°时流体网格的变化图。等到气动力响应基本稳定后,输入对应的各阶位移激励,从而得到对应偏角下的各阶广义气动力系数响应。

图8 机翼柔性后缘偏转前后网格变化Fig.8 Grid changes before and after flexible trailing edge deflection
在训练马赫数为0.9 时,后缘偏角为0°、2°、4°、6°时的颤振马赫数分别为0.202、0.203、0.211、0.224。可以看出,随着后缘偏角的增大,颤振马赫数相比无偏角情况有一定的提高。
3.2 阵风响应分析计算
取马赫数为0.7 工况下计算1-cos 阵风响应,图9 所示为阵风尺寸分别为60m、90m、140m 时柔性后缘偏角为6°下的机翼各阶模态位移响应。可以看出,在该工况下,飞机遭遇阵风响应随着阵风尺寸的增大,模态位移响应呈下降趋势。
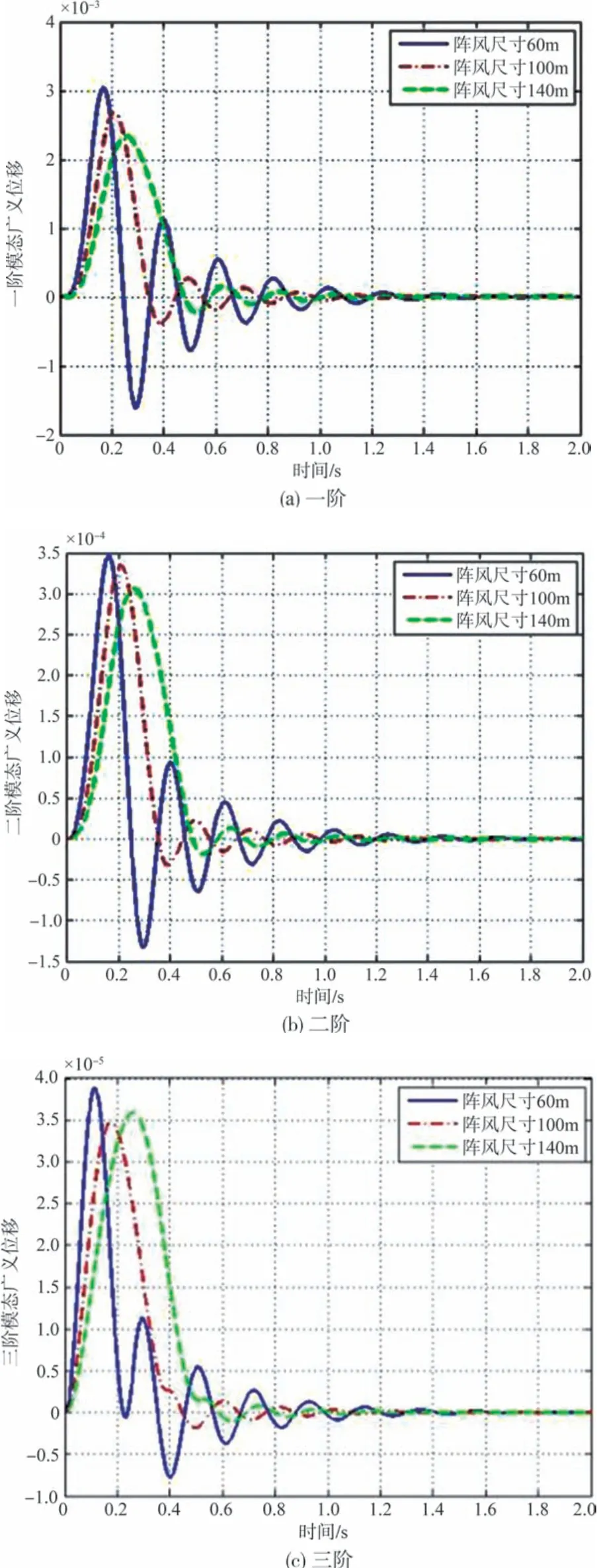
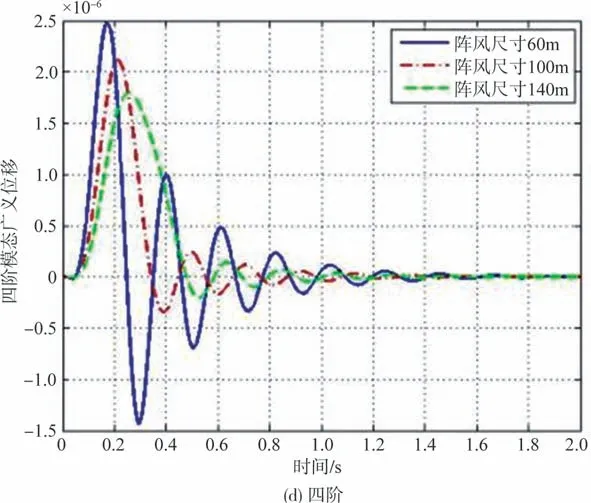
图9 模态位移时域响应Fig.9 Time domain response of modal displacement
4 结论
本文提出一种基于气动降阶模型建立柔性后缘可变形机翼气动弹性分析方法,应用于柔性后缘可变形机翼的颤振特性和阵风响应分析计算。通过结构有限元方法得到各阶模态,将各阶模态变形导入CFD 计算,得到对应的气动力,基于ARX 方法得到气动状态空间模型,耦合结构状态空间模型从而建立可变形机翼的气动弹性状态空间模型,用于可变形机翼气动弹性颤振特性分析和阵风响应计算。研究结果表明,随着后缘偏角的增大,颤振马赫数相比无偏角情况有一定的提高。在马赫数为0.7的工况下,随着阵风尺寸的增大,模态位移响应呈下降趋势。本文尚未考虑柔性后缘结构变形对气动弹性特性的影响,可在后续工作中综合考虑结构气动影响的气动弹性特性。

